文章信息
- 田晶, 任畅, 王一恒, 熊富全, 雷英哲
- TIAN Jing, REN Chang, WANG Yiheng, XIONG Fuquan, LEI Yingzhe
- 对生成Stroke的自身最大适合策略的改进
- Improvement of Self-Best-Fit Strategy for Stroke Building
- 武汉大学学报·信息科学版, 2015, 40(9): 1209-1214
- Geomatics and Information Science of Wuhan University, 2015, 40(9): 1209-1214
- http://dx.doi.org/10.13203/j.whugis20140455
-
文章历史
- 收稿日期: 2014-06-14
2. 武汉大学地理信息系统教育部重点实验室, 湖北 武汉, 430079
2. Key Laboratory of Geographic Information System, Ministry of Education, Wuhan University, Wuhan 430079, China
道路网中的Stroke是根据特定连接规则和生成策略将道路段连接成道路链[1, 2],中文称为路划[3]。Stroke的概念提出至今,对与道路网相关的研究产生了重要影响。生成Stroke通常作为道路网综合[4, 5, 6, 7, 8, 9, 10, 11]、拓扑分析[12, 13, 14]、示意性地图生成[15]、模式识别[16]等研究的首要步骤。
生成道路网Stroke需要回答路段能否相连和路段怎样连接两个关键问题。连接规则回答了路段能否相连,而生成策略回答了路段怎样相连。连接规则主要有几何规则、专题规则以及混合规则[15]。几何规则由Gestalt原则中的“好的延续性”原则导出,主要指两条路段的转折角小于阈值,专题规则主要是指道路同名或道路等级相同,混合规则是指同时考虑几何规则和专题规则。生成策略主要有每对最大适合策略(every-best-fit,EBF)、自身最大适合策略(self-best-fit,SBF)、自身适合策略(self-fit,SF)[16]。
就生成策略而言,每对最大适合策略的优势在于产生的结果一般而言是确定的,但缺陷是极有可能陷入局部最优。自身最大适合策略是可控制的随机策略,其随机性表现在起始路段的选择以及形成一条Stroke后新的起始路段的选择,一旦这些起始路段选择较好,便很有可能跳出局部最优,得到较好的结果。自身适合策略在连接规则确定后是完全随机的策略,难以控制。文献[2]设计了一种统计道路交叉点处两类错误的评价指标对Stroke生成方法进行比较,认为每对自身最大适合策略是最优策略,然而,对于自身最大适合策略以及自身适合策略,该文并没有提及重复多次生成不同的结果,一次生成的结果并不能很好地说明自身最大适合策略与自身适合策略的优劣。文献[17]根据网络参量与交通流量的相关关系,认为自身最大适合策略是最好的策略,能够更好地凸现自组织自然道路。然而,自身最大适合策略在实际应用中存在一定困难,如道路网综合与分析是基于确定的Stroke生成结果来进行的,由于自身最大适合策略生成的Stroke集是不确定的,通过一次生成的结果无法确定综合结果。更进一步,假定每次生成的结果都不理想,就得重复生成多次,在文献[17]的研究中是20次生成后取平均值的结果,这阻碍了自身最大适合策略的应用。鉴于此,本文在这个方面进行一些尝试,对自身最大适合策略进行了改进。
1 对自身最大适合策略的改进 1.1 自身最大适合策略自身最大适合策略是指从任一路段R开始,搜索与其最适应(即最大程度满足连接规则,如转折角最小)的路段R_best,对R_best,搜索与其最适合的路段。生成一条Stroke后,再随机选择一条没有被处理的路段,重复上述过程,直到所有路段均被处理。
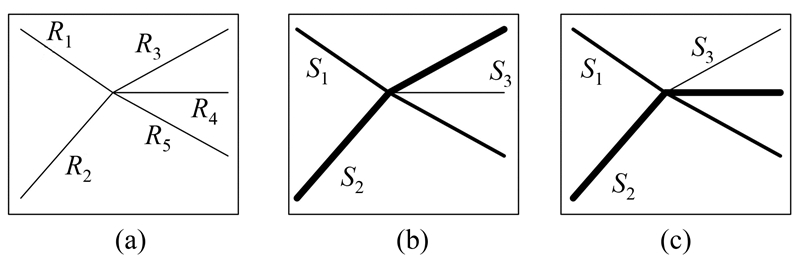
以几何连接规则为例(即仅考虑路段间的转折角),如图 1(a)所示,假定以路段R1为起始路段,则R1和R5连接,形成一条Stroke S1,假定再以R2为起始路段,则R2和R3连接,生成S2,得到如图 1(b)所示的结果。假定以R5为起始路段,则R5和R1连接,形成一条Stroke S1,假定再以R4为起始路段,则R4与R2连接,生成S2,得到如图 1(c)所示的结果。起始路段的选择以及形成一条Stroke后的新的起始路段的选择导致了生成的Stroke集不同。
|
| 图 1 自身最大适合策略示例 Fig. 1 Illustration of Self-Best-Fit Strategy |
本文对自身最大适合策略进行了两个方面的改进。第一,通过确定起始路段以及生成一条Stroke后的新的起始路段,从而达到确定路段处理顺序的目的,起始路段的确定由道路的重要度决定。第二,将与路段s“最适合”的路段t定义为路段t是与路段s满足连接条件的路段中重要度最大的路段。改进的具体方法是:选择最重要的路段作为起始路段,搜索与其“最适合”的路段,生成一条Stroke;然后,从未处理的路段中再次选择最重要的路段作为新的起始路段,生成Stroke,直到所有路段均被处理。
确定道路重要度主要有4种方法:(1)规则法,即定义属性参数的优先顺序来确定道路重要度[9];(2)影响法,删除某条道路,判断其对道路网的影响[10];(3)参量生成法,将某一个或者某几个参量进行变换或集成,生成新的参量来描述道路重要度[3, 7];(4)权重法,对属性参数赋予权重,重要度即为参数的加权和[11]。由于权重法较为直观,应用广泛,本文采用文献[11]使用的权重法确定路段的重要性,其基本思想是运用路段的长度、连通度、接近度、中介度,由CRITIC方法[18]加权,得到道路的重要度,其中路段参量的含义见表 1。引入对偶图的概念,图的节点表示路段,边代表路段与路段相交的关系。形式化定义为G=G(V,E),V是节点的集合,V={v1,v2,…,vn},E是边的集合,E={vi,vj}。图可由其邻接矩阵表示为R(G)=[rij]n×n,其中

当然,也可采用其他的重要度定义方法。
| 参量名称(英文) | 意义 | 计算方法 |
| 长度 | 路段的长度 | |
| 连通度 | 与该路段相交的其他路段的数量 | 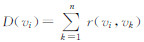
|
| 接近度 | 该路段到所有其他路段的最少连接数量,反 映了其他路段聚集于该路段的可能性 | 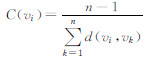 ,其中,d(vi,vk)表示节点vi和vk的最短距离 ,其中,d(vi,vk)表示节点vi和vk的最短距离
|
| 中介度 | 度量了该路段处于其他路段之间的程度,度 量路段是否起“桥梁”作用 | 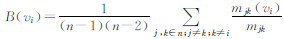 ,其中,mjk表示节点vj和vk间最短路径的数量; mjk(vi)表示节点vj和 ,其中,mjk表示节点vj和vk间最短路径的数量; mjk(vi)表示节点vj和vk间最短路径中经过节点vi的数量。 |
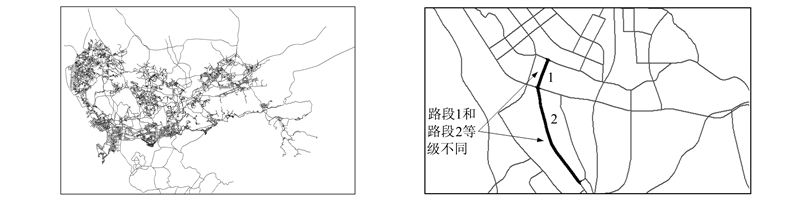
实验数据为深圳市1∶ 1万道路网(见图 2),该道路网具有规则网格模式与不规则模式混合的道路网模式。检查数据的拓扑连通性。
|
| 图 2 深圳市1∶1万道路网 Fig. 2 Shenzhen Road Network at Scale 1∶10 000 |
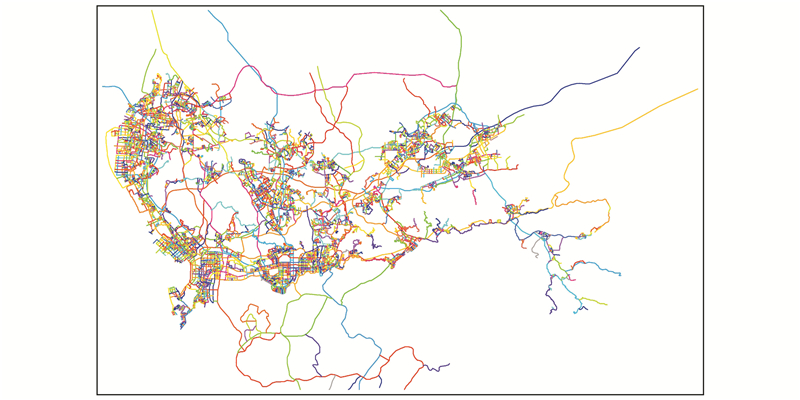
本文实验在路段连接规则方面仅采用几何准则,理由为:(1)由文献[2]的研究结论可知,几何连接规则与每对最大适合策略的组合生成的Stroke能得到较好的综合结果,连接规则中加入了专题规则虽然在结果准确度上有所改进,但改进在统计意义上不显著;(2)文献[17]的研究中仅考虑了几何规则。(3)用肉眼感觉应该相连的路段会因为等级不同而不能连接,如图 3。几何准则即路段间的转折角,阈值定为60°,这个经验值源自文献[2]和文献[19]的经验,生成结果见图 4。当然,本文提出的方法很容易扩展至运用其他连接规则的情况。

|
| 图 3 由于等级不同而不能连接的路段示例 Fig. 3 Road Segments that Cannot be Concatenated Due to Different Hairarchies |
|
| 图 4 改进的自身最大适合策略生成的Stroke Fig. 4 Stroke Buliding by Modified Self-Best-Fit Strategy |
由于路段处理顺序由重要度确定,一般而言,路段的重要度理论上是不相同的。就实际而言,重复生成多次Stroke集,发现生成的Stroke集均相同,所以可以认为由本文提出的改进方法可生成的Stroke结果是确定的。
为说明改进的效果,从与网络功能与视觉认知两个方面进行评价。文献[2]设计了一种统计道路交叉点处两类错误的评价指标对Stroke生成方法进行评价,其核心思想是根据各种策略生成的Stroke结果在道路交叉点处是否与地图综合结果一致来进行评价。文献[17]是通过生成的Stroke是否能很好地反映网络参量与交通流量的相关关系进行评价,其核心思想是通过生成的Stroke是否能很好地将交通流量与对应的描述参量关联来进行评价。同时,这两种评价方法都是针对特定应用,需要特殊数据(同一地区多比例尺路网,交通流量数据)的支持。目前还没有研究从网络功能的角度来对结果进行评价,所以本文尝试引入复杂网络理论中常用的全局效率来对Stroke生成结果进行评价。网络的全局效率由文献[20]提出,该指标描述网络中的节点如何交互,反映了网络中信息传播的顺畅程度,是网络功能方面的全局指标,对于网络G,节点i与节点j间的效率εij反比于其最短路径dij,即εij = 1/dij。网络G的平均效率定义为:
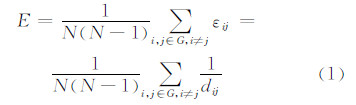
令Gid为网络G的完全图形式,则网络G的全局效率Eglob定义为:
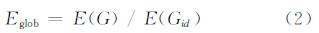
假定道路网是由其对偶形式表示的网络,即路段对应于网络的节点,路段是否相交对应于网络的边。该网络中的节点i到节点j的最短路径长度定义为连接节点i到节点j的最少的边数。由于这样形成的网络的完全图形式,其平均效率为1,所以该网络的平均效率即为其全局效率。如式(1),其中N为路段总数,dij为连接路段i到路段j的最少的步数,即路径长度。全局效率的取值范围为[0, 1]。
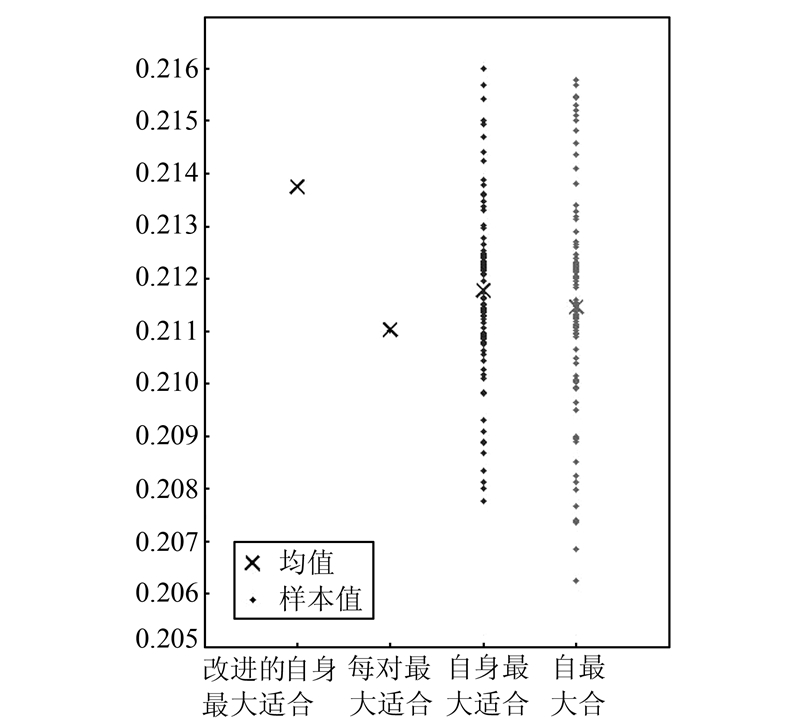
运用全局效率对4种Stroke生成策略产生的结果进行比较,对每种生成策略进行100次实验。如图 5,其中第1列是本文方法生成的Stroke结果对应的全局效率值,第2~4列是运用文献[17]的方法生成的Stroke结果对应的全局效率值。研究发现:(1)由改进的自身最大适合策略和每对最大适合策略生成的Stroke集是确定的,而由自身最大适合策略与自身适合策略生成的Stroke集是不确定的,这一点符合预期。(2)在网络功能方面以全局效率作为评价指标,改进的自身最大适合策略(0.213 8)优于每对最大适合策略(0.211 0);就平均水平而言,改进的自身最大适合策略(0.213 8)优于自身最大适合策略(0.211 8)和自身适合策略(0.2115);就单次结果而言,改进的自身最大适合策略(0.213 8)次于自身最大适合策略和自身适合策略在本次实验中的最优解0.216 0和0.215 8。
|
| 图 5 基于全局效率的4种策略比较 Fig. 5 Comparative Analysis of Four Different Strategies Based on Global Efficiency |
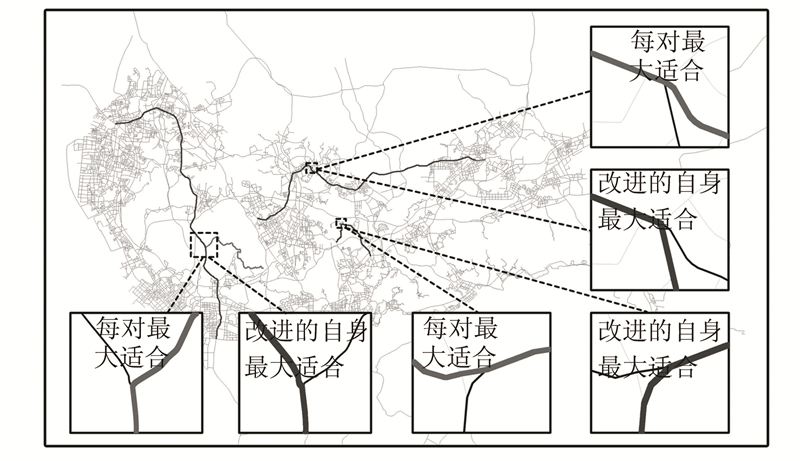
在视觉认知方面,仅与每对最大适合策略进行比较,其原因是自身最大适合策略和自身适合策略生成的Stroke结果是不确定的,仅用其一次生成结果无法有效说明问题。图 6 显示了本方法与每对最大适合策略的主要差异。改进的自身最大适合策略比每对最大适合策略更易形成较长并具有全局性的Stroke。由此可知,本文提出的方法能生成更符合认知规律的Stroke。
|
| 图 6 改进的自身最大适合策略与每对最大适合策略在视觉上的主要差异 Fig. 6 Major Differences from Visual Aspects Between Modified-Self-Best-Fit and Every-Best-Fit Strategy |
本文对生成Stroke的自身最大适合策略进行了改进。基于路段重要度规定路段处理顺序并扩展最适合路段的定义。结果表明:(1)一般而言由改进的自身最大适合策略生成的Stroke是确定的,即对同一道路网,每次用本文算法产生的Stroke集相同。(2)在视觉认知方面,改进的自身最大适合策略比每对最大适合策略更易形成较长并具有全局性的Stroke。(3)在网络功能方面,就平均水平而言,改进的自身最大适合策略优于每对最大适合策略、自身最大适合策略和自身适合策略;就单次结果而言,改进的自身最大适合策略次于自身最大适合策略和自身适合策略的最优解。
进一步的研究主要在两个方面展开:(1)由于生成Stroke通常作为道路网分析与综合的首要步骤,应该对本文的改进进行道路网分析与综合方面的实证研究。(2)Stroke生成问题是一个典型的组合优化问题,本文的改进实质上是一种启发式方法,运用优化理论与方法解决Stroke生成问题将是研究的重点。
| [1] | Thomson R C, Richardson D E. The “Good Continuation” Principle of Perceptual Organization Applied to the Generalization of Road Networks[C]. The 19th International Cartographic Conference, Ottawa, 1999 |
| [2] | Zhou Qi, Li Zhilin. A Comparative Study of Various Strategies to Concatenate Road Segment into Strokes for Map Generalization[J]. International Journal of Geographical Information Science, 2012, 26(4): 691-715 |
| [3] | Xu Zhu, Liu Caifeng, Zhang Hong, et al. Road Selection Based on Evaluation of Stroke Network Functionality[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 769-776(徐柱, 刘彩凤, 张红, 等. 基于路划网络功能评价的道路选取方法[J]. 测绘学报, 2012, 41(5): 769-776) |
| [4] | Edwardes A J, Mackaness W A. Intelligent Generalization of Urban Road Networks[C]. GIS Research UK Conference, York, 2000 |
| [5] | Chaudhry O, Mackaness W. Rural and Urban Road Network Generalization Deriving 1∶250 000 from OS MasterMap[EB/OL]. www.era.lib.ed.ac.uk/bitstream/1842/1137/1/ochaudry001.pdf, 2001 |
| [6] | Zhang Qingnian. Road Network Generalization Based on Connection Analysis[C]. The 11th International Symposium on Spatial Data Handling, Leicester, UK, 2004 |
| [7] | Chen Jun, Hu Yungang, Zhao Renliang, et al. Road Data Updating Based on Map Generalization[J]. Geomatics and Information Science of Wuhan University, 2007, 32(11): 1 022-1 027(陈军, 胡云岗, 赵仁亮, 等. 道路数据缩编更新的自动综合方法研究[J]. 武汉大学学报·信息科学版, 2007, 32(11): 1 022-1 027) |
| [8] | Tomko M, Winter S, Claramunt C. Experiential Hierarchies of Streets[J]. Computers, Environment and Urban Systems, 2008, 32 (1):41-52 |
| [9] | Liu Xingjian, Zhan B F, Ai Tinghua. Road Selection Based on Voronoi Diagrams and “Strokes” in Map Generalization[J]. International Journal of Applied Earth Observation and Geoinformation, 2009, 12: 194-202 |
| [10] | Touya G. A Road Network Selection Process Based on Data Enrichment and Structure Detection[J]. Transactions in GIS, 2010, 14(5):595-614 |
| [11] | Luan Xuechen, Yang Bisheng, Zhang Yunfei. Structural Hierarchy Analysis of Streets Based on Complex Network Theory[J]. Geomatics and Information Science of Wuhan University, 2012, 37(6): 728-732(栾学晨, 杨必胜, 张云菲. 城市道路复杂网络结构化等级分析[J]. 武汉大学学报·信息科学版, 2012, 37(6): 728-732) |
| [12] | Porta S, Crucitti P, Latora V. The Network Analysis of Urban Streets: A Dual Approach[J]. Physica A, 2006, 369: 853-866 |
| [13] | Jiang Bin, Claramunt C. Topological Analysis of Urban Street Networks[J]. Environment and Planning B, 2004, 31: 151-162 |
| [14] | Jiang Bin. A Topological Pattern of Urban Street Networks: Universality and Peculiarity[J]. Physica A, 2007, 384: 647-655 |
| [15] | Li Zhilin, Dong Weihua. A Stroke-Based Method for Automated Generation of Schematic Network Maps[J]. International Journal of Geographical Information Science, 2010, 24(11): 1 631-1 647 |
| [16] | Heinzle F, Ander K H. Characterising Space via Pattern Recognition Techniques: Identifying Patterns in Road Networks[M] //Mackaness W A, Ruas A, Sarjakoski L T. Generalisation of Geographic Information: Cartographic Modelling and Applications. Amsterdam: Elsevier, 2007 |
| [17] | Jiang Bin, Zhao Sijian, Yin Junjun. Self-organized Natural Roads for Predicting Traffic Flow: A Sensitivity Study[J]. Journal of Statistical Mechanics: Theory and Experiment, 2008, 2008(7): 8-18 |
| [18] | Diakoulaki D, Mavritas G, Papayannakis L. Determining Objective Weights in Multiple Criteria Problems: The CRITIC Method[J]. Computers & Operations Research, 1995, 22(7): 763-770 |
| [19] | Jiang Bin, Liu Chengke. Street-Based Topological Representations and Analyses for Predicting Traffic Flow in GIS[J]. International Journal of Geographical Information Science, 2009, 23(9): 1 119-1 137 |
| [20] | Latora V, Marchiori M. Efficient Behavior of Small-World Networks[J]. Physical Review Letters, 2001, 87(19):1-18 |
 2015, Vol. 40
2015, Vol. 40


