文章信息
- 沈占锋, 夏列钢, 程熙, 胡晓东, 骆剑承
- SHEN Zhanfeng, XIA Liegang, CHENG Xi, HU Xiaodong, LUO Jiancheng
- 等值线追踪生成等值面过程中的算法策略
- Algorithm Strategies in the Process of Contour Line Tracing and Contour Surface Generation
- 武汉大学学报·信息科学版, 2015, 40(9): 1201-1208
- Geomatics and Information Science of Wuhan University, 2015, 40(9): 1201-1208
- http://dx.doi.org/10.13203/j.whugis20130621
-
文章历史
- 收稿日期: 2013-10-30
2. 成都理工大学地球物理学院, 四川 成都, 610059
2. Chengdu University of Technology, College of Geophysics, Chengdu 610059, China
在GIS与遥感、地形分析、机械建筑等应用领域中,等值线与等值面是两种非常重要的数据表达方法[1],而基于栅格数据的等值线/等值面生成算法在地形等高线图、等温线(场)图等的数据可视化中有着广泛的应用需求[2]。目前,基于栅格数据生成等值线的算法研究较多[3, 4, 5, 6]。其中,涉及的插值算法有趋势面法、距离反比法、多元回归法、克里金插值法等[7, 8, 9, 10],平滑算法有线性平滑、多次平滑、最小二乘平滑、负指数加权平滑、Bezier曲线法、样条平滑等[11, 12, 13]。然而,较为详细且效率较高的等值面追踪方法研究却很少。文献[2, 14]试图直接通过等值点的计算与连接实现区域等值面的生成,但实现等值点有序连接与等值线/面平滑的算法复杂,推广难度大。更多的解决方案集中于基于栅格数据的等值线的生成,然后再在此基础上通过各等值线关系判断实现等值面的追踪,如文献[15, 16],但现有这些算法不仅缺少等值面内岛的处理过程,也没有等值面间拓扑关系判断方法的具体说明,而这些是实现各等值面属性拓扑分析、属性推理的重要步骤。
本文结合散点数据或栅格数据的等值面生成的需求,首先在等值线生成的基础上,针对等值线追踪的方法给出了数据结构与算法流程;然后,分别对区域内的岛与非岛的等值线进行追踪并形成闭合曲面;最后,通过拓扑分析实现闭合曲面间的空间邻接关系确定与属性推理,完成栅格数据的等值面构造过程。
1 等值线追踪方法流程等值面可由生成的等值线通过等值线追踪策略来实现。等值面可视为由一条或多条等值线构成的一个闭合区域,该区域能够采用某种填充方案进行填充,用以表示在某个等值线区间(等值线的值可以指高程值,也可以指温度、水深、气压等其他用来生成等值面的值,本文以高程值为例,其他类似)的区域范围。采用某种填充方案填充并生成等值面的过程又称为等值线填充[1]、等值线跟踪[17]、等值线追踪[18]等。等值面具有以下性质。
1) 每条等值线均有一个属性字段表示其高程值,本文假定该高程字段名称为elv,等值线的值从小到大分别为elvi(i=1,2,…,n),类型为数值型(如double、float、int等);对于等值面来说,也存在一个高程字段elv,其类型为字符型(如string等),而其属性值有3种可能:“
2) 与等值线一样,等值面具有空间拓扑性(相邻等值面的高程属性值具有可递推性),据此可以进行等值面elv字段的拓扑分析与推理赋值。
3) 最终生成的等值面区域Map将会与原始数据的区域相对应,假设最终通过等值线追踪生成的等值面分别为P1,P2,…,Pn,则有:Pi∩Pj=NULL(i≠j;i,j=1,2,…,n),P1∪P2∪…∪Pn=Map,且Pi与Pj(i≠j;i,j=1,2,…,n)的elv属性值可能相同。
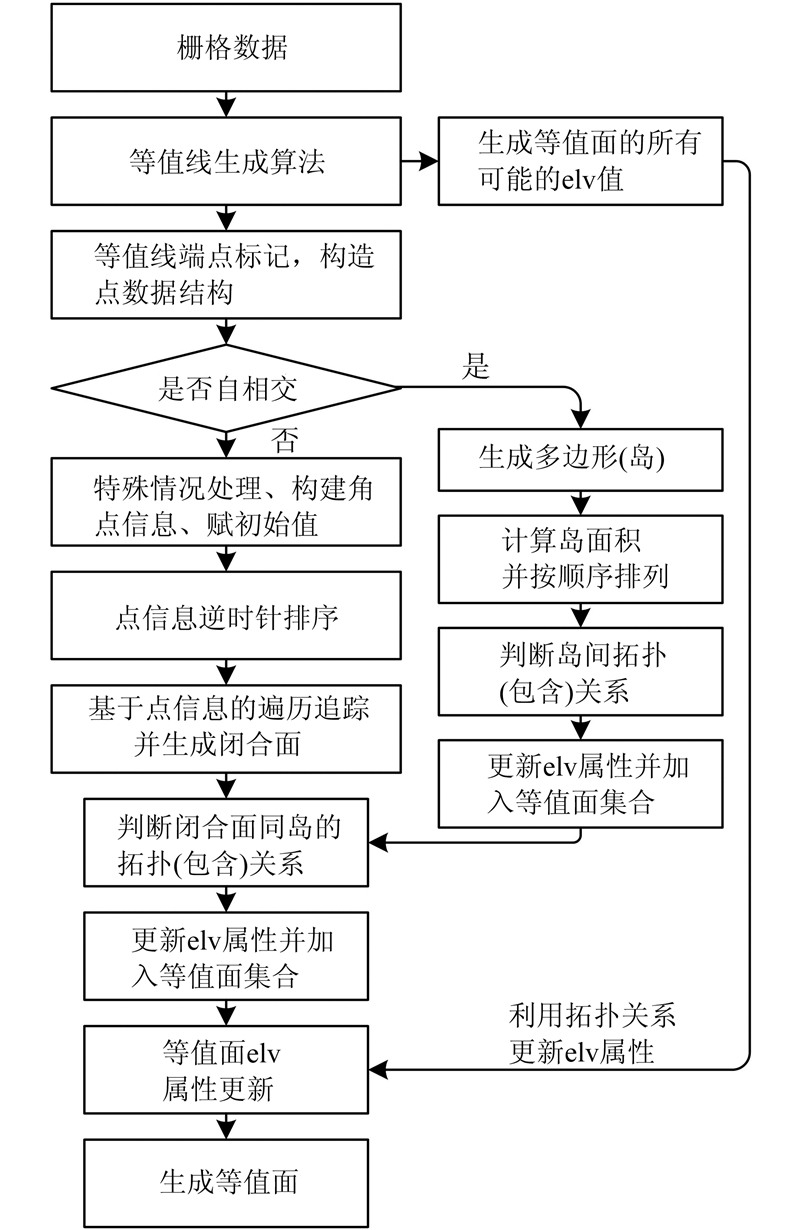
图 1表示了本文等值线追踪及等值面生成流程图,并根据以上性质进一步实现了等值面间的拓扑关系分析及等值面的属性递推。
|
| 图 1 等值线追踪与等值面生成流程图 Fig. 1 Flowchart of Contour Line Tracing and Contour Surface Generation |
由图 1可知,等值线的追踪步骤为:首先,采用某种等值线的生成算法实现基于栅格数据的等值线生成,可以采用GDAL库的GDALContourGenerate()函数实现,并由已经输入的等值线属性值生成等值面的高程属性值序列,相应的等值面高程值序列采用string类型表示,其取值方法由等值面的性质1决定。然后,遍历所有等值线的端点,记录所有的端点及构造数据结构(见本文§2.1),并判断该等值线的首尾是否相交(见§2.2)。如果相交,证明此等值线为一闭合曲线,直接生成等值面集合中的一个岛;如果不自相交,则该等值线一定与待生成等值面的矩形区域边界有交点。最后,根据这些交点信息逆时针进行等值线追踪并生成闭合曲面(§2.3),并判断闭合曲面同已经生成的岛的邻接关系,更新其高程属性并完成等值面的追踪过程(§2.4)。
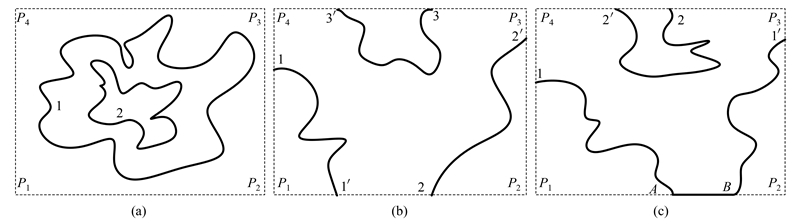
2 等值面生成算法实现 2.1 等值线端点信息处理区域内等值点的顺序连接所形成的曲线即为等值线,一条等值线可能与区域边界相交并形成2个端点,也可能不与边界相交,据此可以判断该等值线对应的等值面是否为岛。因此,在等值线的追踪过程中,需先对构造等值线的端点信息进行存储,并基于这些端点信息进行闭合曲面追踪及岛信息判断。图 2列举了基于几种常见的等值线追踪生成等值面的情形。
|
| 图 2 几种常见的等值线图 Fig. 2 Several General Contour Line Chart |
在理想情况下,基于栅格数据生成的等值线均为封闭的闭合曲线,并由此能够构造对应的等值面,如图 2(a)。但是,由于研究区域有限,不可能生成一个无限大的等值线/面图,因此等值线很多时候将会被研究区域的边界分割为一系列具有高程属性的线,如图 2(b)所示。对于图 2(a)的情况而言,可以根据其生成的岛及各个岛间的空间关系进行拓扑判断,并完成区域的等值面生成,但是对于一个区域内仅有1个elv属性值的情况而言(如图 2(a)中的两条等值线的elv值均为9),则无法对等值面间的关系进行判断,也无法确定各等值面的属性值,还需要辅助一个非等值线上的点,这可以从原始栅格数据中取一个边界角点辅助判断,其具体算法实现见§2.2。对于图 2(b)的情况而言,则需要根据第1节中的性质3将区域内各部分进行连接构成区域内的等值面,再根据各等值面间的拓扑关系进行其elv属性的推理。同样地,如果图 2(b)中的几条等值线具有相同的elv属性,此时也需要辅助另外一个非等值线上的点实现等值面elv属性的推理,其闭合面的追踪过程见§2.3。对于图 2(c)所示的特殊情况而言,当一条等值线同研究区域的交点多于两个时,则需要对这种特殊的情况进行处理,即将该等值线进行拆分,将图 2(c)的等值线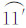 拆分为等值线
拆分为等值线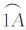 及
及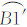 ,并去掉线AB,再采用与图 2(b)相同的等值线追踪方法来实现等值面的追踪。
,并去掉线AB,再采用与图 2(b)相同的等值线追踪方法来实现等值面的追踪。
等值线的端点信息存储是判断等值线是否为岛及等值线追踪的基础,其数据结构定义的信息量将直接决定等值线追踪算法的效率,因此,本文中需要对构成区域内等值线的端点信息进行记录。相应的数据结构定义为:
typedef struct _PointInfo
{
OGRPoint point;//被标记的端点
double elv;//该等值线Feature的高程值
int*times;//记录该点追踪次数的计数器
_PointInfo*theOther;//该Feature的另一端点
OGRLineString*lineString;//该Feature对应的等值线
OGRFeature*firstFeature;//该Feature相邻的第一等值面
OGRFeature*secondFeature;//该Feature相信的第二等值面
bool operator < (const _PointInfo& right) {…}//用于排序
bool operator == (const _PointInfo& right){…}//用于判断相等
}PointInfo;
在此数据结构中,需要记录该端点的高程、计数器、另一个端点、相邻的两个等值面等信息。其中,point变量记录了该点的坐标信息,高程elv变量记录了其高程值,计数器变量times则用于记录该点对应的等值面追踪次数的指针,变量theOther指向了与该端点对应的等值线的另一个端点(如果其坐标与此点相同,则说明此等值线对应的多边形为岛)。同时,采用变量firstFeature、secondFeature分别记录该端点两侧的等值面,并通过这两个等值面的elv高程值来推断新构造的等值面的高程值elv。
2.2 岛的生成与处理当等值线的端点与边界不相交时,该等值线(一定为闭合曲线)自身可以形成闭合曲面,形成该区域等值面中的一个岛。对于图 2(a)而言,该区域的等值面将由外区域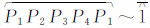 、岛
、岛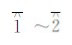 、及岛
、及岛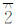 等3部分构成(~符号表示去除)。当某等值线的首尾端点相同时,则可对等值线上的点序列直接调用多边形生成函数OGRPolygon:: addRing()来生成岛多边形。为了进一步判断不同岛的拓扑关系,需要构造岛的数据结构,可采用以下数据结构进行实现:
等3部分构成(~符号表示去除)。当某等值线的首尾端点相同时,则可对等值线上的点序列直接调用多边形生成函数OGRPolygon:: addRing()来生成岛多边形。为了进一步判断不同岛的拓扑关系,需要构造岛的数据结构,可采用以下数据结构进行实现:
struct ISLAND
{
OGRPolygon*polygon;//对应的多边形
double area;//面积
double elv;//外环高程值
OGREnvelope env;//外接矩形
OGRPolygon*pParent;//父多边形
vector<OGRPolygon*>*pChilds;//子多边形
bool operator < (ISLAND& right){…}//用于排序
};
采用§2.1中所述的数据结构对当前范围内的所有等值线的端点信息进行存储,并根据等值线的起点与终点是否相同来判断该等值线所对应的等值面是否为岛,如果是岛则赋予上述数据结构信息。根据上述数据结构,一个岛的信息应该包含构成该岛的多边形、面积、高程值、外接矩形、父多边形(1个)、子多边形(0或多个)等;同时,岛间需要能够实现根据面积的快速排序(可通过STL的sort()函数实现)以便于岛间包含关系判断。根据图 1,对岛的处理流程为:首先,采用OGR提供的OGRPolygon::get_Area()函数进行多边形面积的快速计算,然后调用此数据结构中的排序函数进行面积排序(可降序排列),最后对排序好的岛间拓扑(包含)关系进行判断,如果岛内还存在岛,则需要将岛内的岛进行排除并更新岛的面积属性(可采用OGRLinearRing:: addSubLineString()与OGRPolygon:: addRing()函数实现)。
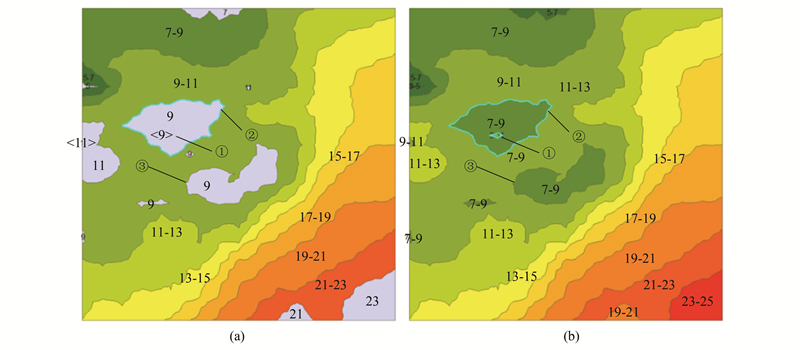
图 3为对不同的岛间关系判断的结果示意图。当完成图中多个岛的识别之后,需要判断面积较大的多边形是否包含面积较小的多边形(首先判断他们的外接矩形,即上面数据结构中的env,再进一步判断不同几何对象间的关系),并在此数据结构中记录相应的父子关系。根据图 3,在完成①、②所指示的两个岛的多边形构造之后,进一步判断出岛②包含了岛①,因此,需要将岛①所对应的区域从岛②中去除(可以采用OGR提供的函数OGRGeometry::Difference()进行实现)并更新其面积属性,而图 3中的岛③与其他的岛没有包含关系。最终记录各岛间的包含关系并加入到生成的等值面集合中。
|
| 图 3 岛间拓扑关系判断 Fig. 3 Topology Relationship Analysis Between Different Islands |
对于图 2(b)所示的非岛等值线而言(实际上,图 2(c)也可通过前期处理转化成为图 2(b)的样式),首先采用§2.1中的数据结构对与边界相交的端点信息进行记录,再对相应的端点进行排序,然后基于这些边界点信息进行区域闭合多边形的追踪,形成相应的闭合曲面,最后再判断这些闭合曲面同已经生成的岛的包含关系,确定各岛的父多边形,并更新相应的高程elv属性,从而完成等值面的生成过程。根据本文§1中等值面的性质(3)可知,图 2(b)所示的等值面由面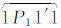 、
、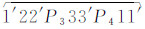 、
、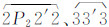 等4部分构成,在这些等值面的追踪过程中,基于相应的点信息的遍历追踪策略尤为重要,将直接决定等值线追踪的效率与鲁棒性,本节将重点对此进行介绍。
等4部分构成,在这些等值面的追踪过程中,基于相应的点信息的遍历追踪策略尤为重要,将直接决定等值线追踪的效率与鲁棒性,本节将重点对此进行介绍。
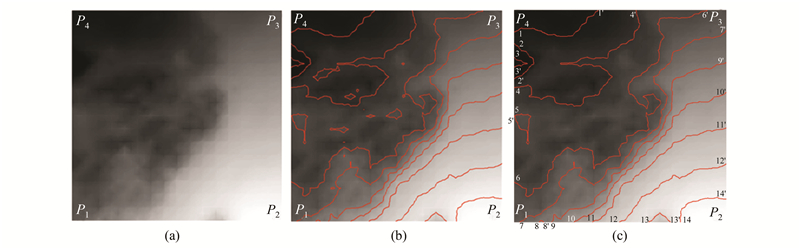
图 4示意了栅格数据生成等值线及等值线追踪形成等值面的过程。其中,图 4(a)为原始栅格数据,图 4(b)为生成的等值线,图 4(c)为去除其中的岛后而进行的等值线编号。对于生成的等值线而言,需先对相应的等值线中的所有线(Feature)的两个端点进行编号,如图 4(c)所示。编号的规则是从左上角开始,依次向左下角、右下角、右上角、左上角的方向进行遍历,编号自1开始。同时,将被标记的点所在Feature的另一个端点标记为1′,每个标号的端点信息采用§2.1中定义的数据结构来实现。
|
| 图 4 等值线追踪过程中的端点编号 Fig. 4 End Points Number for Contour Line Tracing |
根据上述数据结构,可以记录该端点的各种信息,并按照一定的规则进行追踪形成闭合面(等值面)。相应的追踪规则分两个步骤。
1) 需要基于图 4(c)所示的所有Feature的端点构造一个有向链表或数组,结构类似于:
vector
vector
vector
vector
vector
其中,LU_LB、LB_RB、RB_RU、RU_LU分别记录的是与左、下、右、上边相交的点的信息,且按逆时针的方向对相应的点进行排序;而在结构allPoints_Seq中则按顺序记录了LU_LB、P1、LB_RB、P2、RB_RU、P3、RU_LU、P4等点信息的指针,即结构allPoints_Seq中的点是按照逆时针进行组织的。其中,4个角点的P1、P2、P3、P4的PointInfo结构体中仅有OGRPoint point及int times等两个有效属性,其他的属性均可赋值为NULL,且其times的属性的初始值为1(即非特殊情况下角点处仅位于一个等值面中)。
2)对等值面的搜索算法与策略按的实现方式为:对于allPoints_Seq,沿其存储的点信息数据向下搜索,如图 4(c)所示,先从左上角沿左边开始搜索,当搜索到一个点后(本例中为点1),再根据上述数据结构快速找到该点对应的另一点(即数据结构中的theOther,本例中为点1′),再沿点1′继续搜索,得到左上角点P4,再得回点1,形成左上角的闭环(等值面)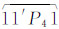 。搜索结束后,更新相应的点1、点1′、P4的相应的信息(*times在原有的基础上增加1,并将闭合曲面加入生成的等值面集合中)。继续搜索下一个点,并判断该点的*times的值是否为2,如果为2则继续下一点进行搜索,直到allPoints_Seq中的所有点的times均为2。对于此例来说,沿点1向下搜索,得到点2,根据点2的PointInfo*结构体得到该环的另一端点2′,继续搜索,得到点4、4′、1′、1,搜索结束并得到闭合面
。搜索结束后,更新相应的点1、点1′、P4的相应的信息(*times在原有的基础上增加1,并将闭合曲面加入生成的等值面集合中)。继续搜索下一个点,并判断该点的*times的值是否为2,如果为2则继续下一点进行搜索,直到allPoints_Seq中的所有点的times均为2。对于此例来说,沿点1向下搜索,得到点2,根据点2的PointInfo*结构体得到该环的另一端点2′,继续搜索,得到点4、4′、1′、1,搜索结束并得到闭合面 。按此方法,分别得到闭合面
。按此方法,分别得到闭合面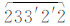 ,闭合面
,闭合面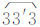 ,闭合面
,闭合面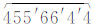 ,闭合面
,闭合面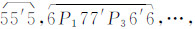 直到完成所有闭合面的搜索过程。
直到完成所有闭合面的搜索过程。
等值面拓扑信息更新包括等值面中岛间关系的确定,以及不同闭合面及岛间的拓扑关系的确定,并以此更新相应等值面的高程属性值。其中,岛间关系的确定已在§2.2节中有所说明,需要进一步分析追踪形成的闭合面同岛的包含关系,并对岛进行有效性标记,其实现方法是对等值面与岛的空间关系进行判定(可以采用OGRGeometry::Contains()函数分别对两个多边形的外接矩形及其多边形进行分别判定实现),并进一步更新等值面的高程、面积等属性,完成基于栅格数据的等值面的构造过程。
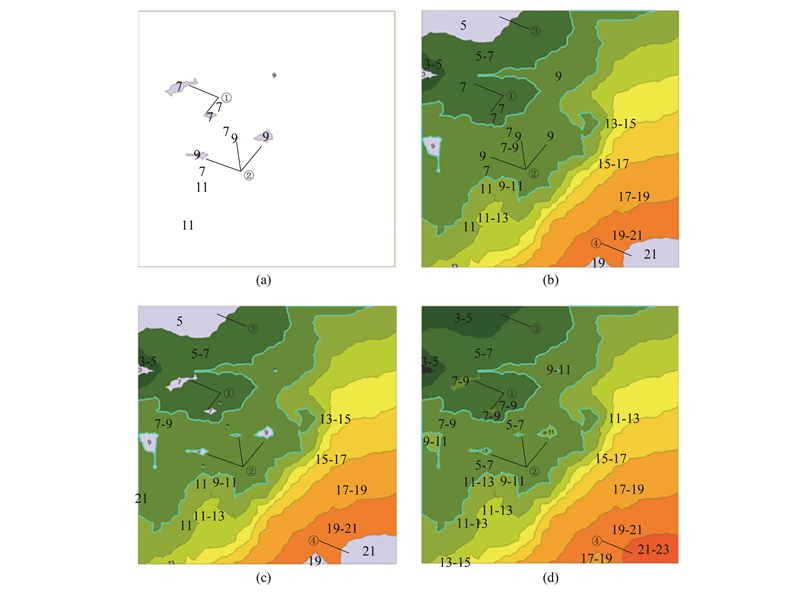
图 5(a)示意了采用§2.2策略实现的研究区域中岛信息的提取,图 5(b)示意了采用§2.3的等值线追踪策略实现等值面信息的追踪,图 5(c)则对图 5(b)中新生成的等值面与图 5(a)中已经生成的岛间的空间关系进行判断,并去除其中岛的区域,图 5(d)是最终完成的等值面图。对比图 5中标记为①、②的区域可知,在图 5(a)完成岛的识别之后,图 5(b)通过等值线追踪实现了其他非岛区域的等值面生成,在经过图 5(c)的空间拓扑关系分析后实现了岛同非岛区域的区分,直到图 5(d)完成了相应的高程信息elv的更新(可对比图中的标注信息,即elv高程值)。图 3中的①、②等处也同样示意了等值面拓扑更新(岛间拓扑确立)前后的颜色变化(并应用不同颜色进行充填)。
|
| 图 5 基于等值线追踪原理的等值面生成过程 Fig. 5 Procedure of Contour Surface Generation Based on Contour Line Tracing |
在图 5(c)至图 5(d)的属性更新过程中,需要对相应的各等值面多边形的属性进行赋值(见图 1),即对各个多边形Polygon的高程值(elv字段)进行赋值。赋值方法分两种情况,一种是该等值面由两个不同高程值的等值线经追踪而成(即两条等值线的PointInfo结构体中的elv变量值不同),这时该Polygon的elv属性值即是由这两条等值线的elv值所构成的区间组成,如某个Polygon的高程值为“9-11”。另一种则是该等值面只由单一elv的等值线构成,如与区域边界相交的多边形区域或一些孤立的岛等,这些等值面的高程值需要根据其相邻的等值面的高程值进行拓扑关系递推得出。为提高算法效率,需判断两个多边形是否为邻接关系:首先判断两个多边形的外接矩形是否相交(根据数据结构中的env变量),再应用OGRGeometry::Touches()函数进行判断。标记完后就可以应用该属性值对等值面进行不同颜色设色,效果如图 5所示,直到所有的等值面的高程值均符合一定的规则为止,如本文实例中的所有等值面的elv字段中均会带有“-”、“<”、“>”(见§1中的的性质1)。
3 实验与效率分析根据图 1及§2中针对等值面的追踪与拓扑判断过程可知,区域等值面的构造过程的算法效率主要取决于区域中岛的数量及与边界相交的等值线数量两个因素。而这两个因素实际上由数据的“坡度”及用户指定的等值线“密度”决定,算法的耗时与区域中岛的个数及等值线的条数成正比。根据§2.2与§2.4,岛的处理过程分为两步:第1步是判定其是否为岛并实现区域等值面的构造,此过程的效率决定于采用OGR生成新Feature的效率,几乎没有耗时;第2步为岛间拓扑关系判断并实现岛等值面高程属性elv的更新过程,此过程一方面需要判断该岛是否包含比其面积小的岛,另一方面在进行elv推断时还需要根据该岛周围的elv值推断该岛的高程elv。同样,根据§2.3及§2.4,对于边界相邻的等值线构造的等值面来说也需要两步,第1步为采用§2.3实现的等值线追踪过程,第2步为对该等值面进行elv属性的赋值过程(也可能需要相邻等值面的拓扑关系进行确定)。相比来说,在等值线构造等值面的过程中,岛的处理效率比非岛的效率高,而进行拓扑分析时非岛的算法处理要比岛的处理效率高。
本文对等值线追踪及等值面拓扑关系判别的算法采用Visual C++.NET来实现,测试环境为Dell i-5 2.6 GHz、4 GHz内存的笔记本,操作系统为Windows 7。等值面追踪及拓扑关系建立总共耗时为0.056 s,达到了较高的算法效率,效果如图 5(d)所示。在基于网络环境IPM-MyHome环境上,对我国东海地区气温变化等值面图进行实时生成与渲染,其效率与效果能够满足实际的应用需求(如等值面实时生成、形成动画模式的气温变化等)。
4 结 语本文提出了基于等值线的追踪原理来实现区域等值面的快速构造方法,该算法具有较好的鲁棒性与较高的追踪效率。本文算法给出了等值线追踪过程中需要的两个重要的数据结构,分析了岛间拓扑关系判别方法,并在此基础上给出了等值面属性推理方法,最后对相应的算法进行了效率分析。实验及实际应用表明,本文算法能够实现栅格数据(如气温数据、高程数据等)的等值面快速生成,并基于生成的等值面实现其属性值的拓扑推理,进而可针对不同的应用进行进一步的颜色充填等。同时,本文算法亦可广泛应用于气象、水文、地质等领域中的等值面快速生成。
| [1] | Codrea M C, Nevalainen O S. Note: An Algorithm for Contour-Based Region Filling[J]. Computers & Graphics, 2005, 29: 441-450 |
| [2] | Yu Zhaohai, He Bing. An Isosurface Construction Method Based on Vector Field Structure[J]. Computer Simulation, 2008, 25(2): 90-92(于兆海, 何兵. 一种基于矢量场结构的等值面构造方法[J]. 计算机仿真, 2008, 25(2): 90-92) |
| [3] | Wang K Y, Qin Q H, Kang Y L. A Modified Isoparametric Mapping Fill Method to Display Color Mapping of Data[J]. Advances in Engineering Software, 2004, 35: 585-591 |
| [4] | Chi Baoming, Li Zhijun, Ye Yong, et al. Study on the Arithmetic of Automatically Drawing Isoline of Ground Water Level Based on GIS[J]. Journal of Jilin University (Earth Science Edition), 2007 37(2): 261-265 (迟宝明, 李治军, 叶勇, 等. 基于GIS的地下水水位等值线图自动生成算法研究[J]. 吉林大学学报(地球科学版), 2007, 37(2): 261-265) |
| [5] | Oka S, Garg A, Varghese K. Vectorization ofContour Lines from Scanned Topographic Maps[J]. Automation in Construction, 2012, 22: 192-202 |
| [6] | Zhang Dengrong, Liu Shaohua, Mao Tianlu, et al. An Algorithm of Automatic Creation of Topological Relation and its Application of Fast Color Fill Between Contours[J]. Journal of Image and Graphics, 2001, 6(3): 224-231(张登荣, 刘绍华, 毛天露, 等. 等值线自动建立拓扑关系算法与快速填充应用[J]. 中国图象图形学报, 2001, 6(3): 224-231) |
| [7] | Yu Jia, Wu Xu. A Modified Contour Tracing Algorithm of Rectangular Grid[J]. Journal of Henan Normal University (Natural Science), 2008, 36(6): 34-37(于嘉, 吴旭. 一种改进的矩形网格等值线追踪算法[J]. 河南师范大学学报(自然科学版), 2008, 36(6): 34-37) |
| [8] | Perlibakas V. Automatical Detection of Face Features and Exact Face Contour[J]. Pattern Recognition Letters, 2003, 24: 2 977-2 985 |
| [9] | Ren M W, Yang W K, Yang J Y. A New and Fast Contour-Filling Algorithm[J]. Pattern Recognition, 2005, 38: 2 564-2 577 |
| [10] | Li Jiwang, Meng Zhijun, Geng Wei. The Application of Equivalent Line and Equivalent Surface Generative Algorithm in Variable Fertilization of Precision Agriculture[J]. Chinese Agricultural Science Bulletin, 2006, 22(2): 404-407 (李吉旺, 孟志军, 耿伟. 等值线和等值面生成算法在精准农业变量施肥中的应用[J]. 中国农学通报, 2006, 22(2): 404-407) |
| [11] | Chen J, Qiao C F, Zhao R L. A VoronoiInterior Adjacency-Based Approach for Generating a Contour Tree[J]. Computers & Geosciences, 2004, 30: 355-367 |
| [12] | Wagenknecht G. AContour Tracing and Coding Algorithm for Generating 2D Contour Codes from 3D Classified Objects[J]. Pattern Recognition, 2007, 40: 1 294-1 306 |
| [13] | Li Qiang, Li Chao, Gan Jianhong. Study on Algorithm of Isoline Filling Based on Triangle Mesh[J]. Computer Engineering and Applications, 2013, 49(5):185-190 (李强, 李超, 甘建红. 基于三角网的等值线填充算法研究[J]. 计算机工程与应用, 2013, 49(5): 185-190) |
| [14] | Zou Yanhong, He Jianchun. A Spatial Shape Simulation Method for Three Dimensional Geological Body Based on Marching Cubes Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 910-917 (邹艳红, 何建春. 移动立方体算法的地质体三维空间形态模拟[J]. 测绘学报, 2012, 41(6): 910-917) |
| [15] | Wu Ziyin, Gao Jinyao. A Fast Algorithm of Color Fill Between Contours Based on Grid Data[J]. Acta Geodaetica et Cartographic Sinica, 1999, 28(4): 350-354 (吴自银, 高金耀. 一种基于格网的快速等值线充填算法[J]. 测绘学报, 1999, 28(4): 350-354) |
| [16] | Tang Zidong, Zheng Mingxi, Wang Siqun, et al. A New Automatic Filling Algorithm Between Contours Based on Triangulation Net[J]. Journal of Image and Graphics, 2009, 14(12): 2 577-2 583(汤子东, 郑明玺, 王思群. 一种基于三角网的等值线自动填充算法[J]. 中国图象图形学报, 2009, 14(12): 2 577-2 583) |
| [17] | Hou Fengzhen, Zhuang Jianjun, Ning Xinbao. Isoline Drawing Algorithm and Programming Implementation Based on Case Table[J]. Journal of Nanjing University (Natural Sciences), 2008, 44(4): 371-380 (侯凤贞, 庄建军, 宁新宝. 基于构型表的等值线绘制算法及程序实现[J]. 南京大学学报(自然科学), 2008, 44(4): 371-380) |
| [18] | Chang Hui, Chai Huabin, Zou Youfeng. Isoline Tracing Technique Based on Search-Circle[J]. Science of Surveying and Mapping, 2009, 34(2): 119-121 (常会, 柴华彬, 邹友峰. 基于搜索圆法的等值线追踪技术[J]. 测绘科学, 2009, 34(2): 119-121) |
 2015, Vol. 40
2015, Vol. 40


