文章信息
- 陈静, 刘婷婷, 侯小波
- CHEN Jing, LIU Tingting, HOU Xiaobo
- 面向虚拟地球的多尺度矢量数据可视化方法
- Virtual Globe-Oriented Visualization Method of Multi-scale Vector Data
- 武汉大学学报·信息科学版, 2015, 40(9): 1195-1200
- Geomatics and Information Science of Wuhan University, 2015, 40(9): 1195-1200
- http://dx.doi.org/10.13203/j.whugis20130532
-
文章历史
- 收稿日期: 2013-09-26
网络三维虚拟地球利用网络优势向用户提供全球多尺度、交互式、分布式的空间信息,使得海量地理信息服务和处理的方式从原来的集中、独占走向分布、共享,现有网络三维虚拟地球系统对于矢量空间数据的可视化多采用栅格化的方式,具有较好的符号特征表达,能够提供面向公众的三维可视化服务,但是,相对于几何绘制的机制,这种方式没有保留矢量数据的空间特征,难以实现矢量空间对象的拾取操作,也不利于矢量空间对象的查询和分析[1]。
基于几何绘制的相关研究主要集中在单机环境下矢量数据与多尺度地形数据叠加和可视化方法[2, 3]。在基于球面剖分模型将矢量数据与地形数据集成的研究方面,文献[4]提出用三角裁剪有向无环图这种数据结构将二维矢量数据与多分辨率地形格网的关系记录下来,在绘制时将其解析以提高可视化的效率;文献[5, 6]分别基于等经纬度球面剖分模型和球面退化四叉树格网模型将矢量数据无缝叠加到DEM格网中,主要侧重于矢量数据在球面上的绘制方法,没有将矢量数据与球面离散网格进行集成建模。文献[7]基于球面三角四叉树剖分模型探讨了基于球面离散网格的三维矢量数据的组织,但是没有集成地形模型。文献[8]基于球面退化四叉树格网模型,针对几何叠加方法中插值相交计算复杂这一问题,提出了矢量线数据与地形数据集成的“漂移”算法,提高了可视化的效率,但是相关实验主要集中在本地客户端进行。
在应用方面,Google Earth对矢量数据基于几何机制的可视化表达侧重于小比例尺,对于大比例尺矢量数据仍采用栅格化的表达方式;World Wind基于插件机制,在客户端加载矢量数据;ArcGlobe采用预先矢量数据栅格化方式,供客户端集成显示。
综上所述,相关研究侧重于单机环境下矢量数据与球面网格模型和地形数据的集成可视化,同时,矢量数据与地形数据内插生成的三维矢量数据具有一定的数据冗余,面向网络环境的高效可视化需要在保证可视化效果的前提下,减少数据传输量。对此,本文基于球面离散网格将矢量数据与地形数据叠加进行分块组织,针对可视化效果和网络传输要求,对分块数据进行压缩处理,探讨网络环境下面向虚拟地球的多尺度矢量数据可视化方法。
1 面向虚拟地球的矢量数据结构已有较多球面离散格网方法,其中,等经纬球面离散格网模型易于对全球范围进行四叉树结构索引,检索效率高,适合全球多尺度地形数据、影像数据集成组织。基于上述因素,本文选择等经纬度的球面离散格网作为球面剖分模型。
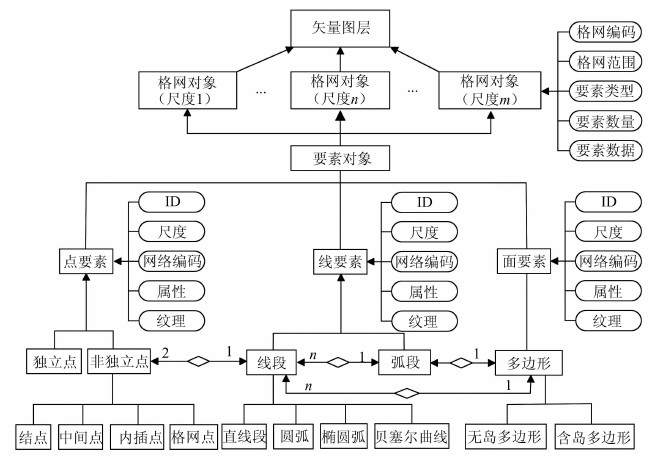
基于统一的大地坐标系统,采用几何叠加的方法将全球矢量数据与多尺度地形数据叠加,构建面向虚拟地球的多尺度矢量数据结构,如图 1所示。矢量数据按照图层进行组织,并与多层次等经纬度离散网格,以及网格对应尺度的全球地形数据进行无缝集成,形成不同尺度的矢量数据。每一个尺度的矢量图层都由全球等经纬度格网对象组成,格网对象封装了其格网范围内的矢量数据及其相关信息,包括格网编码、格网范围、要素类型、要素数量、要素数据等。矢量数据分为点、线和面这三类基本要素。每一个矢量数据从二维矢量数据进行扩展,具有二维矢量数据的地图比例尺的信息。同时,每一个矢量数据也具有与二维矢量数据对象一致的ID标识、属性、纹理等特征,并且还具有全球离散网格编码的属性,一个要素可能跨多个离散网格,因此,一个要素对象可能包含多个不同的网格编码。在此基础上,根据各个要素的不同特征,分为独立点、非独立点、线段、弧度和多边形等5类对象。其中,依据非独立点与球面离散网格、地形集成的不同条件,又分为格网点、内插点、结点和中间点4类。结点为线段或弧段的起点和终点,决定了它们的方向;中间点为构成弧段的点要素中除去起结点和终结点的点,它决定了弧段的形状。
|
| 图 1 面向虚拟地球的多尺度矢量数据结构 Fig. 1 Data Structure of Virtual Globe-Oriented Multi-scale Vector |
上述面向虚拟地球的多尺度矢量数据结构具有以下特点:(1)面向虚拟地球。以全球离散格网为块单元,对传统二维矢量数据进行分块,并且对块中的要素进行分类和抽象,便于与虚拟地球中分块组织的影像、地形数据集成与表达。(2)多尺度特征。对于同一比例尺矢量数据,不仅对应于全球多层次离散格网,并且与格网对应多尺度的地形数据进行集成,从而具有多尺度特征。
2 多尺度矢量数据的分块构建与数据组织方法本文基于上述面向虚拟地球的多尺度矢量数据结构,提出了面向虚拟地球的多尺度矢量数据分块构建与组织方法。
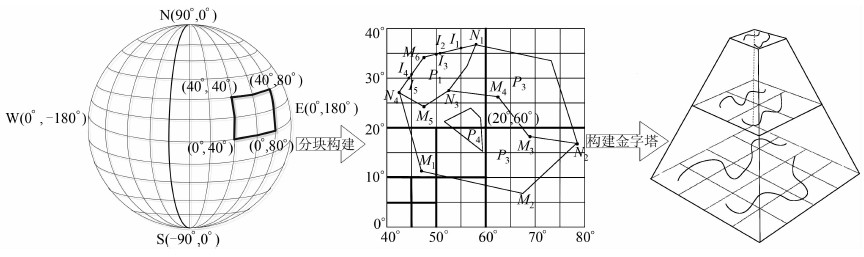
矢量数据的分块构建是指以全球等经纬度离散格网为块单位,分别获取格网范围内的矢量数据与相应尺度的全球地形数据,然后进行叠加,构建面向虚拟地球的矢量数据。在矢量数据分块的过程中,对于点要素只需要根据经纬度判断所在的瓦片,而线要素和面要素则存在与球面离散格网相交的情况。将产生的交点定义为格网点,如图 2所示,弧段N1N4与全球等经纬度格网相交产生格网点I1、I2、I3、I4和I5,被截为6段,分布于不同的格网中,类似地,多边形P1、P2和P3也跨越多个格网。二维矢量数据与地形数据叠加时,点要素可以直接通过内插计算出高程,但是对于线要素和面要素,如果仅计算构成点的高程值,就会出现“悬空”或者“入地”的现象,使得矢量数据不能贴伏于地表,因此需要增加二维矢量数据与地形格网的交点,即内插点。基于这种方法,当同一个矢量数据与不同尺度的地形格网叠加时,就会产生不同详细程度的内插点,在可视化调度时,要确保对应矢量数据与地形数据的同步调度和无缝匹配。同时考虑到交互可视化过程中在相邻不同级别的瓦片接边处矢量数据有可能不连续,需要首先重构地形格网,再将矢量数据与重构后的地形网格求交,以保证矢量数据的连续性。
|
| 图 2 面向虚拟地球的矢量分块构建与组织示意图 Fig. 2 Virtual Globe-Oriented Tile-Based Construction and Organization Method of Vector Data |
矢量数据的分层组织通过将矢量与多尺度全球等经纬度离散格网集成来实现。将同一比例尺的矢量数据与多尺度全球等经纬度离散格网叠加,可以形成多尺度矢量数据,而多尺度全球等经纬度离散格网与全球地形模型的尺度一一对应,从而面向虚拟地球的矢量数据的分层与全球地形模型尺度也一一对应,也就实现了面向虚拟地球的矢量数据的分层多尺度构建。
在此基础上,按照矢量数据的图层的概念,以一个比例尺的图层为单元,将图层中的矢量数据进行分层分块组织,形成一个比例尺图层的面向虚拟地球的分层分块的金字塔结构矢量数据集,如图 2所示。以此类推,可以构建多比例尺、多个图层的面向虚拟地球的分层分块的金字塔结构矢量数据集。
3 面向可视化的矢量数据压缩方法构建矢量数据集之后,对于线要素和面要素,有些内插点分布非常密集,并且高程非常相近,甚至可能相等,造成数据冗余。同时,在场景渲染时,如果两个或者多个共面矢量数据同时绘制,将会在Z-Buffer中保存相同的Z值(通常是浮点数取整造成的),从而出现Z-Buffer 冲突现象。对此,设计了面向可视化的Douglas-Peucker矢量数据压缩算法,对线要素以及面要素的边界进行压缩。
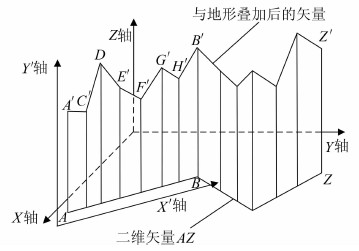
Dauglas-Peucker算法是一种常用而有效的矢量数据压缩算法,其使用的一个重要前提条件是所处理的矢量线对象位于同一个平面,而二维矢量线对象数据和地形数据叠加后形成三维空间中的矢量,不处于同一个平面上,因此不能直接对生成的矢量对象使用Douglas-Peucker压缩算法。如图 3所示,二维矢量线对象AZ和地形叠加后生成空间矢量弧段A′Z′,在X轴和Y轴构成的平面中A′Z′不共面,但是在A′ABB′平面上组成AZ的直线段AB生成的矢量弧段A′B′共面,即A′B′是一条平面曲线,于是像A′B′这样的矢量弧段就可以用Douglas-Peucker算法来进行压缩,A′B′曲线段中C′、D′、E′、F′、G′和H′这些新增的内插点就是压缩的对象。
|
| 图 3 二维矢量及其与地形叠加后的矢量 Fig. 3 Two-Dimensional Vector and Result Vector After Superposition with Terrain |
考虑到弧段A′B′具有高程信息,因此对Douglas-Peucker算法基于以下三点进行扩展:(1)采用点到线段的高程差作为限差,即多大的高程差内可以保证压缩后矢量可视化的效果,如图 3中将点C′到直线A′B′的竖直距离而不是垂直距离与设定的限差比较。采用高程差作为限差,不仅比垂距容易计算,而且也使得该算法在地形平坦的地区压缩率较高,在地形起伏较大的地区压缩率较低,更贴近实际情况。(2)为了避免出现Z-Buffer 冲突现象,在设定限差时将矢量数据做适当的抬高处理,使矢量数据不会因为Z-Buffer 冲突被遮挡。(3)在矢量数据压缩完以后,如果有被舍去的点位于弧段上方,则说明该弧段会有部分点被埋在地形格网之下,因此对这部分点需进行适当保留,从而避免矢量数据被地形遮挡。
根据以上三点,矢量数据压缩算法的基本步骤为:(1)以线状矢量数据中共面的弧段为单位,以该弧段在地面的投影为X轴,高程方向为Y轴,建立一个平面坐标系,如图 3中的X′轴和Y′轴;(2)连接弧段的首尾两点,计算所有的中间点到首尾两点所确定的直线的竖直距离,即高程差;(3)选取其中高程差最大的点,如果该点的高程差小于给定的限差,则弧段上的所有中间点都舍去;(4)如果该点的高程差大于给定的限差,则该点作为第一个保留点,通过该点把弧段分成两个弧段,对每条弧段重复步骤(1)至(4)直到完成压缩过程;(5)检查压缩后的弧段数据,看有没有被舍去的点位于压缩后的弧段之上,如果没有,算法结束,如果有,找出距离弧段高程最大的点,将其保留,通过该点将弧段分成两段,重复执行直到压缩后的弧段上方没有点。
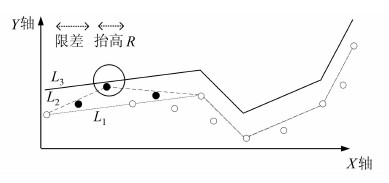
根据面向可视化的Douglas-Peucker算法对图 4中的数据进行压缩,图中弧段L1是按照算法的(1)~(4)步进行压缩处理的结果,可以看到有部分点(实心点)位于L1之上,经过算法第(5)步,得到弧段L2,避免了地形遮挡。弧段L2为没有将矢量数据高程值增加得出的结果,如果将矢量抬高R,则处理后的结果为曲线L3,可以看出,矢量数据高程值增加后,矢量数据得到进一步简化,圈中的点在矢量数据高程值增加后被舍弃。
|
| 图 4 面向可视化的Douglas-Peucker算法示意图 Fig. 4 Algorithm of Visualization-Oriented Douglas-Peucker |
经过反复试验,将矢量数据高程增加值区间设定为0.5~1 m之间,就可以避免Z-Buffer 冲突现象。面向可视化的Douglas-Peucker算法还存在限差如何确定的问题,这也是所有Douglas-Peucker算法共性的问题。限差的大小也应随着可视化中视点高度的不同而变化,在满足矢量可视化的效果下尽可能设得高一些。在视点较低时,限差值应该设置得较低;反之,视点较高时限差值也相应提高。
4 实验与分析根据以上方法,本文采用C++开发了两个实验系统进行验证。实验数据为全球1∶400万国界矢量数据、中国地区1∶100万省界矢量数据、局部地区1∶5万和1∶1万宗地矢量数据。地形数据为全球90 m分辨率SRTM数据,构建了10层分辨率为2倍关系的连续多尺度地形数据集,影像数据为局部0.2 m分辨率影像数据、全球30 m分辨率影像数据、全球1 000 m分辨率影像数据,构建了20层分辨率为2倍关系的连续多尺度影像数据集。
第一个实验系统是面向虚拟地球的多尺度矢量数据分块构建与组织系统VisualVectorBuilder,主要实现二维矢量数据与地形数据、全球等经纬度离散格网的集成,矢量数据的分层分块数据组织。图 5是浏览集成构建后的分块矢量编码等信息。
|
| 图 5 多尺度矢量数据分块与组织 Fig. 5 Organization of Multi-scale Vector Data |
第二个实验系统是基于开放式虚拟地球集成共享平台GeoGlobe进行。图 6(a)为1∶100万中国省界矢量数据与全球SRTM多尺度地形数据集第1层匹配下的可视化效果图,由于视点较高,地形数据分辨率较低,看不到矢量数据的可视化效果。

|
| 图 6 矢量数据可视化效果图 Fig. 6 Visualization of Vector Data |
图 6(b)是同一矢量数据与全球SRTM多尺度地形数据集第10层匹配下,视点贴近地面时看到的矢量可视化的效果图,可以看到图中地形的起伏较大,矢量数据和地形叠加显示效果较好。
图 7是地块查询分析的效果图,可以拾取并高亮显示地块对象,并查询到地块ID。
|
| 图 7 矢量对象拾取示意图 Fig. 7 Selection of Vector Object |
为了验证面向可视化的Douglas-Peucker算法的有效性,采用某地48.8 MB地块二维矢量数据,分别设置3组不同的参数进行对比实验,3组实验数据结果如表 1所示。
| 第一组 (无简化) | 第二组 (限差1 m) | 第三组 (限差1 m,抬高1 m) | |
| 数据集总 量/Bytes | 95 369 898 | 65 249 965 | 46 138 501 |
| 点对象数量/个 | 8 736 | 5 927 | 4 573 |
| 数据量压缩比 | 1 | 1.46 | 2.07 |
| 绘制效果 | Z-Buffer 冲突 | 无Z-Buffer 冲突 | 无Z-Buffer 冲突 |
| 绘制帧率 /(帧/s) | 18 | 21 | 28 |
通过表 1可以看出,采用面向可视化的Douglas-Peucker算法后,不仅实现了矢量数据的简化压缩,而且消除了Z-Buffer 冲突,绘制帧率也相应提高了。在限差1 m、抬高1 m的参数下,压缩比达到2.07。更改算法的参数,压缩率也会变化,这需要在综合考虑地形因素以及可视化效果后确定合适的限差值。
5 结 语本文主要探讨了网络环境下虚拟地球中基于几何绘制的矢量空间数据可视化方法,研究了面向虚拟地球的多尺度矢量数据结构,实现了多尺度矢量数据分块构建与组织,设计了面向可视化的Douglas-Peucker算法,在保证可视化效果条件下,实现了矢量数据的压缩。实验结果表明,该方法在达到约2倍的压缩率、提高约50%的可视化帧率条件下,能够实现三维虚拟地球中多尺度矢量数据可视化,同时易于实现矢量空间对象的拾取和查询操作。下一步将探讨矢量分块多尺度组织后空间对象拓扑关系的重建以及空间分析方法。
| [1] | Sun Min, Zhao Xuesheng, Zhao Renliang. Global GIS and It's Key Technology[J]. Geomatics and Information Science of Wuhan University, 2008, 33(1): 41-45 (孙敏, 赵学胜, 赵仁亮. Global GIS及其关键技术[J]. 武汉大学学报·信息科学版, 2008, 33(1): 41-45) |
| [2] | Schneider M, Guthe M, Klein R. Real-Time Rendering of Complex Vector Data on 3D Terrain Models[C]. The 11th International Conference on Virtual Systems and Multimedia, Ghent, Belgium, 2005 |
| [3] | Yang L, Zhang L Q, Kang Z Z, et al. An Efficient Rendering Method for Large Vector Data on Large Terrain Models[J]. Sci China (Info Sci), 2010, 53(6): 1 122-1 129 |
| [4] | Wartell Z, Kang E, Wasilewski T, et al. Rendering Vector Data over Global Multiresolution 3D Terrain[C]. The Symposium on Data Visualization, Grenoble, Grenoble, France, 2003 |
| [5] | Sun W B, Shan S G, Chen F, et al. Geometry-Based Mapping of Vector Data and DEM Based on Hierarchical Longitude/Latitude Grids[C]. The Second International Conference on Geoscience and Remote Sensing, Qingdao, 2010 |
| [6] | Sun Wenbin, Hu Bailin, Wang Hongbin, et al. Seamless Integration of Vector and Terrain Data Based on Degenerate Quadtree Grid[J]. Geography and Geo-Information Science, 2012, 28(1): 39-42 (孙文彬, 胡佰林, 王洪斌, 等. 基于球面DQG的矢量与地形数据无缝集成[J]. 地理与地理信息科学, 2012, 28(1): 39-42) |
| [7] | Guan Li, Chen Chengqi, Lv Xuefeng. Study on the Organization Model for Vector Data Based on Global Subdivision Grid[J]. Geography and Geo-Information Science, 2009, 25(3): 23-27 (关丽, 程乘旗, 吕雪锋. 基于球面剖分的矢量数据模型研究[J]. 地理与地理信息科学, 2009, 25(3): 23-27) |
| [8] | Wang Jiaojiao. Adaptive Integration Modeling of DEM and Vector Data Based on Special DQG Framework[D]. Beijing: China University of Mining and Technology, 2013(王姣姣. 基于球面DQG的地形与矢量数据自适应集成建模[D]. 北京:中国矿业大学, 2013) |
 2015, Vol. 40
2015, Vol. 40


