文章信息
- 何颂华, 陈桥, 李博
- HE Songhua, CHEN Qiao, LI Bo
- 构建对立信号的光谱降维方法研究
- Spectral Dimension Reduction Method by Building Opponent Signals
- 武汉大学学报·信息科学版, 2015, 40(9): 1188-1194
- Geomatics and Information Science of Wuhan University, 2015, 40(9): 1188-1194
- http://dx.doi.org/10.13203/j.whugis20130426
-
文章历史
- 收稿日期: 2013-08-16
重现与原始样本相匹配的颜色是颜色科学的重要研究方向之一[1]。按照匹配标准的不同,颜色匹配可分成色度匹配、色貌匹配和光谱匹配三个层次。其中,光谱匹配是一种同色同谱的颜色匹配方式,因此也被认为是最理想的颜色匹配方式[2, 3]。但在实现光谱匹配时,如果直接将高维(31维或更高维)的光谱数据用于颜色复制,会占用很大的存储空间,且计算复杂度高,运算时间长。对此瓶颈问题的解决方法就是在光谱匹配前先对光谱反射率图像进行降维处理,去除冗余信息,再将得到的低维光谱数据代替原始高维光谱数据用于颜色复制,从而可有效减少存储空间,提高运算效率[4, 5]。目前常用的光谱降维方法主要采用主成分分析(principal component analysis,PCA)、独立成分分析(independent component analysis,ICA)等多元统计方法[6, 7, 8, 9],但用这些方法将高维光谱降维后再重构的光谱是对原始光谱的一个数学逼近,其在视觉上的色彩还原不是最优的。本文针对这一问题提出新的解决方案,新方案将分别构建表征色度精度和光谱精度的基向量,使得在高光谱图像降维过程中兼顾光谱和色度两方面的匹配精度,并确保所建的低维线性模型在变光源光照条件下能获得好的色度匹配效果。
1 人眼视觉特性对光谱降维的影响光波是一种辐射能。通常来说,光通量越大,感觉光越明亮,这是对同一种波长的光而言。对不同波长的光来说这是不成立的,因为人眼对可见光谱范围内不同波长的光的辐射,具有不同的感受性。即对辐射量相同但波长不同的色光,在视觉上产生的明亮程度是不同的,光谱光视效率正是这一特性的体现。由于人眼有明视觉和暗视觉两种视觉功能,光谱光视效率也分为明、暗两种。由于人眼对颜色的感知是在明视觉条件下进行的,因此,本文只讨论明视觉情况下人眼视觉特性对光谱降维的影响。明视觉光谱光视效率曲线V(λ)的最大值在555 nm处,即眼睛对波长为555 nm的黄绿光最敏感,愈趋向光谱两端的光感觉愈弱。
基于PCA的光谱降维方法,其降维重构后的光谱数据是对原始光谱反射率的数学逼近,但在色彩再现方面,光谱精度高和色度精度高并无必然联系,往往出现光谱误差较小但颜色色差较大的情况。本文以1 269个Munsell色块[10](为便于比较,对这些色块按顺序编号)的基于PCA的光谱重构为例,将重构光谱与原始光谱相比,其光谱均方根误差(spectral root mean square error,sRMS)为0.007 7的色块有6个(见表 1),其sRMS为0.013 3的色块有10个(见表 2)。表 1、2中,色差采用典型光照下的CIELAB标准色差公式ΔEab*进行比较,D50是标准光源。
| 色块编号 | ΔEab*(D50,2°视场) |
| 107 | 1.26 |
| 202 | 1.79 |
| 255 | 0.24 |
| 1 043 | 1.07 |
| 1 079 | 1.55 |
| 1 146 | 1.64 |
| 色块编号 | ΔEab*(D50,2°视场) |
| 48 | 1.07 |
| 141 | 0.83 |
| 270 | 0.49 |
| 310 | 0.44 |
| 574 | 0.80 |
| 745 | 0.24 |
| 935 | 1.19 |
| 1 086 | 2.65 |
| 1 174 | 1.10 |
| 1 188 | 0.96 |
从表 1中可以看出,虽然6个色块的光谱精度都为0.007 7,光谱重构精度较高(低于平均值),但重构光谱与原始光谱相比色差却有明显的差别,有的较大,如202号色块,色差为1.79,有的很小,如255色块,色差仅为0.24。同样,从表 2中可以看出,虽然10个色块的光谱精度都为0.013 3,光谱重构精度较差(高于平均值),但仍然有色度精度表现很好的色块,如745号色块,重构光谱与原始光谱的色差仅为0.24。将表 1和表 2中色差差别最大的两个色块挑选出来,比较其原始光谱与重构光谱的形状差异(见图 1),图 1中,实线为原始光谱,虚线为重构光谱。

|
| 图 1 光谱精度一致的Munsell色块原始光谱与重构光谱形状比较 Fig. 1 Comparisons of Spectral Curves for Two Munsell Samples Which Have Same Spectral Accuracy |
从图 1(a)中可以看出,色差小的255号色块其重构光谱与原始光谱在光谱中间区域(450~650 nm)的差异明显小于色差大的202色块,但在光谱两端区域其形状差异明显大于202色块。
同样,在图 1(b)中色差小的745号色块其重构光谱与原始光谱在光谱中间区域(450~650 nm)的差异明显小于色差大的1 086色块,但在光谱两端区域其形状差异明显大于1 086色块。
这种情况普遍存在于Munsell色块的光谱重构中,重构光谱与原始光谱之间存在最大光谱差的色块,其色差并不是最大;反之,重构光谱与原始光谱之间存在最大色差的色块,其光谱差并不是最大。这充分证明基于主成分分析的光谱降维方法,其重构光谱的光谱精度高低和色度精度高低并无必然联系。其原因在于色度值是光源、颜色物体、标准观察者联合作用的结果,色度精度采用典型光照下的CIELAB标准色差公式ΔEab*进行评价[11]。光谱精度评价采用光谱均方根误差(sRMS)[12],其计算公式的物理意义是重构光谱与原始光谱各个对应波长上的光谱反射率差值的平方和求平均后再开平方根。除非重构光谱与原始光谱完全重合,其色差为零,色度精度当然也就很高。但实际上由于各方面误差的影响,重构光谱与原始光谱不可能完全重合,这样,在整个光谱形状上会出现有些地方重合、有些地方不重合的情况,而色度值受到光源和标准观察者的影响,光源和标准观察者对整个光谱带上不同波长的光谱的作用是不同的,所以最后结果就出现光谱精度很高,但色度精度不高的情况。同样,也会出现色度精度高的重构光谱,其光谱精度可能不高的情况。例如人眼对光谱中间段很敏感,但对光谱两极不敏感,如果重构光谱与原始光谱之间的光谱误差出现在中间段,即使光谱误差sRMS很小,色差也可能很大;如果两者的光谱误差出现在两头,中间段重合得很好,即使光谱差很大,色差也可能很小。
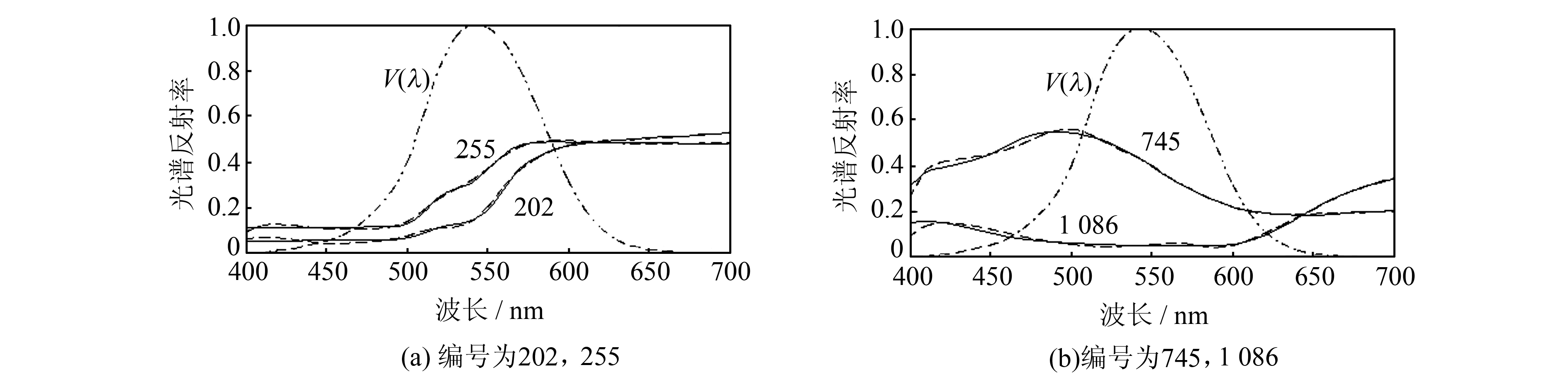
由于光谱光视效率函数v(λ)反映了人眼在明视觉下的灵敏程度,因此进一步将202色块和255色块的重构光谱与光谱光视效率函数进行比较(见图 2(a)),发现在光谱光视效率函数的半高光谱段(510~610 nm)内,255色块的重构光谱与原始光谱重叠性要好于202色块的重叠性,但在其他波段范围内202色块光谱的重叠性要好于255色块。这个结论同样适用于745色块和1 086色块光谱与光谱光视效率函数的比较(见图 2(b))。图 2中,实线为原始光谱,虚线为重构光谱。

|
| 图 2 色块光谱与明视觉光谱光视效率函数的比较 Fig. 2 Comparisons Between Munsell Spectrum and Photopic Spectral Luminous Efficiency Function |
上文的比较分析充分说明在进行光谱图像降维重构时,不能只是考虑光谱形状上的逼近,还要考虑色彩再现过程中人眼视觉特性以及光源的影响。
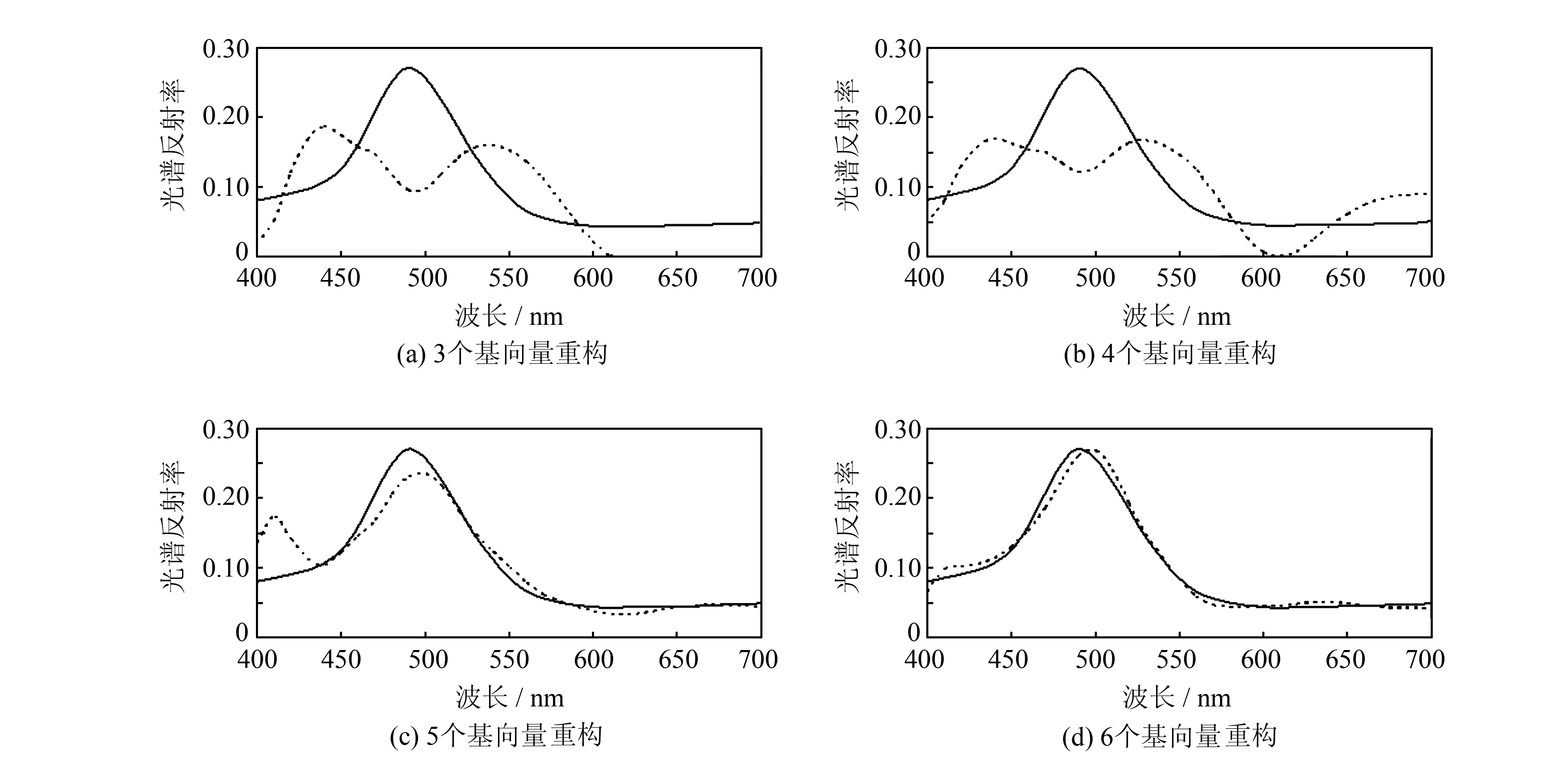
2 构建对立信号的光谱降维法根据颜色视觉理论,颜色视觉过程可以分为两个阶段。第一阶段为视网膜阶段,视网膜内有L-cones、M-cones、S-cones三种独立的视锥细胞。它们选择地吸收光谱不同波长的辐射。其中,S-cones相对来说主要对光谱短波敏感,L-cones对光谱长波敏感,M-cones则对长短之间的中间波段的光谱敏度。同时,每一种视锥细胞又单独产生白和黑的反应,在强光作用下产生白的响应,无光时为黑色响应。第二阶段为视神经传输阶段,色觉的响应兴奋由锥体感受器向视觉中枢的传导过程中,接受信号又重新组合,最后形成三对对立性的神经反应,即红或绿、黄或蓝、白或黑反应。通过以上分析可知,获得的色度信息只需要三个视觉通道的对立信号来完成。那么,在光谱低维线性模型中,是否也可以用三个对立信号光谱代替前三个基向量来表征色度信息,余下的基向量表征光谱信息。基于这一想法,本文提出了一种新的光谱降维表示方法——构建对立信号的光谱降维法(building opposite singles for reducing spectral dimension,BORSD)。
BORSD法基于颜色视觉机理,是在PCA得到的基向量基础上的扩展。在所建的低维线性模型中,前三个基向量由视锥灵敏度L、M、S构建的对立信号得到,模型中的其余基向量由残余光谱通过PCA推导。在构建对立信号时模拟三色颜色信号向对色颜色信号转换的过程,如图 3所示。在从三种锥体细胞刺激向三种对立响应转换时,三色学说的三种锥体细胞的光谱灵敏度曲线也转换成对立学说的相对光谱响应曲线。感红锥体细胞与感绿锥体细胞的光谱灵敏度之差L(λ)-M(λ)就是红-绿对立响应X,L(λ)+M(λ)-S(λ)等于黄-蓝对立响应Y。黑-白对立响应A则与光谱光视效率曲线V(λ)相同,它们都是波长λ的函数。转化关系为:

|
| 图 3 三色颜色信号向对色颜色信号转换过程图 Fig. 3 Conversion Diagram from Three Color Signals to Opponent Signals |
由于转换后的对立响应信号A、X、Y并不是正交的,为了使其与PCA基向量具有相同的正交特性,需对其进行正交化处理,得到正交的对立响应信号A′、X′、Y′(见式(2)),其中G为正交转化矩阵。正交化处理意味着A、X、Y向基向量的转化具有唯一性,并可使转化后的基向量满足式(3)。正交化后得到的基向量本质上是原向量组的一种矩阵旋转,在数学计算上对结果并不会产生影响。
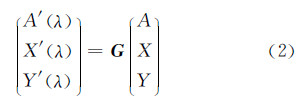
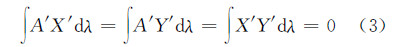
对于一个光谱反射率r(λ),其线性模型可表示为:
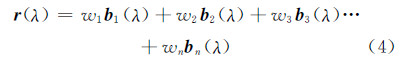
式中,bi(λ)是第i个基向量;wi是基向量对应的权重系数;n是原始光谱的采样维数。在本文算法中,用正交信号A′、X′、Y′代替式(4)中的前三个基向量。这样,由正交信A′、X′、Y′重构的一个光谱反射率为g:
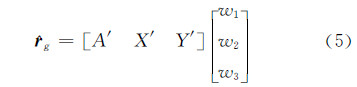
将其推广到一组光谱反射率R,则式(5)可进一步表示为:

式中,Bg是基向量矩阵,由A′、X′、Y′构成;Wg是对应的系数矩阵,可通过最小二乘法满足与原始光谱最小光谱差求得:
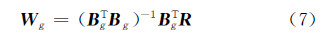
将式(7)代入到式(6),有:
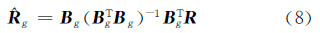
由正交化对立信号A′、X′、Y′重构的光谱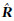 g表征了色度信息,其损失的光谱矢量为:
g表征了色度信息,其损失的光谱矢量为:
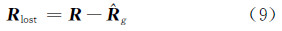
Rlost也称之为残余光谱,可用PCA法求得最佳近似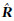 lost ,用
lost ,用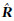 lost对
lost对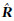 g进行补偿,最终得到与源光谱反射率在色度和光谱两方面均有较好近似的降维重构光谱,其线性模型可表示为:
g进行补偿,最终得到与源光谱反射率在色度和光谱两方面均有较好近似的降维重构光谱,其线性模型可表示为:

式中,Blost 为残余光谱Rlost 通过PCA法推导的特征向量;Wlost为对应的系数矩阵。将式(8)、(9)代入式(10)可进一步表示为:
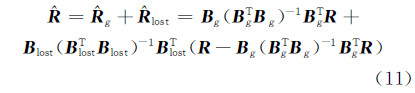
从线性模型式(10)的形式可以看出,BORSD方法本质上将光谱分成两个部分进行降维,第一个部分用正交对立信号表征光谱的色度信息,第二部分用残余光谱对第一部份与源光谱的损失进行补偿,以提高重构光谱的光谱精度。
由于本文低维线性模型在其用于表征色度信息的前三个特征向量的构建上与光源无关,因此在理论上可以提高变光照条件下的色差稳定性。
3 实验与分析选择表色完全,涵盖自然界常见颜色并具有代表性的1 269个Munsell色块作为实验样本,该样本的光谱集数据由Parkkinen所测量[9]。对各个色块的光谱反射率数据在可见光波长范围400~700 nm之间按照10 nm的间隔进行采样,这样,样本数据库可表示成一个1 269×31维的矩阵。为验证变换光照时本文算法的有效性,实验中采用CIE标准照明体A、C、D50、F11这4种光谱功率分布差异明显的标准照明体作为典型光照进行验证。分别从色度精度和光谱精度两方面对降维效果进行评价。色度精度采用典型光照下的CIELAB标准色差公式ΔEab*进行评价,光谱精度评价采用光谱均方根误差(sRMS)。
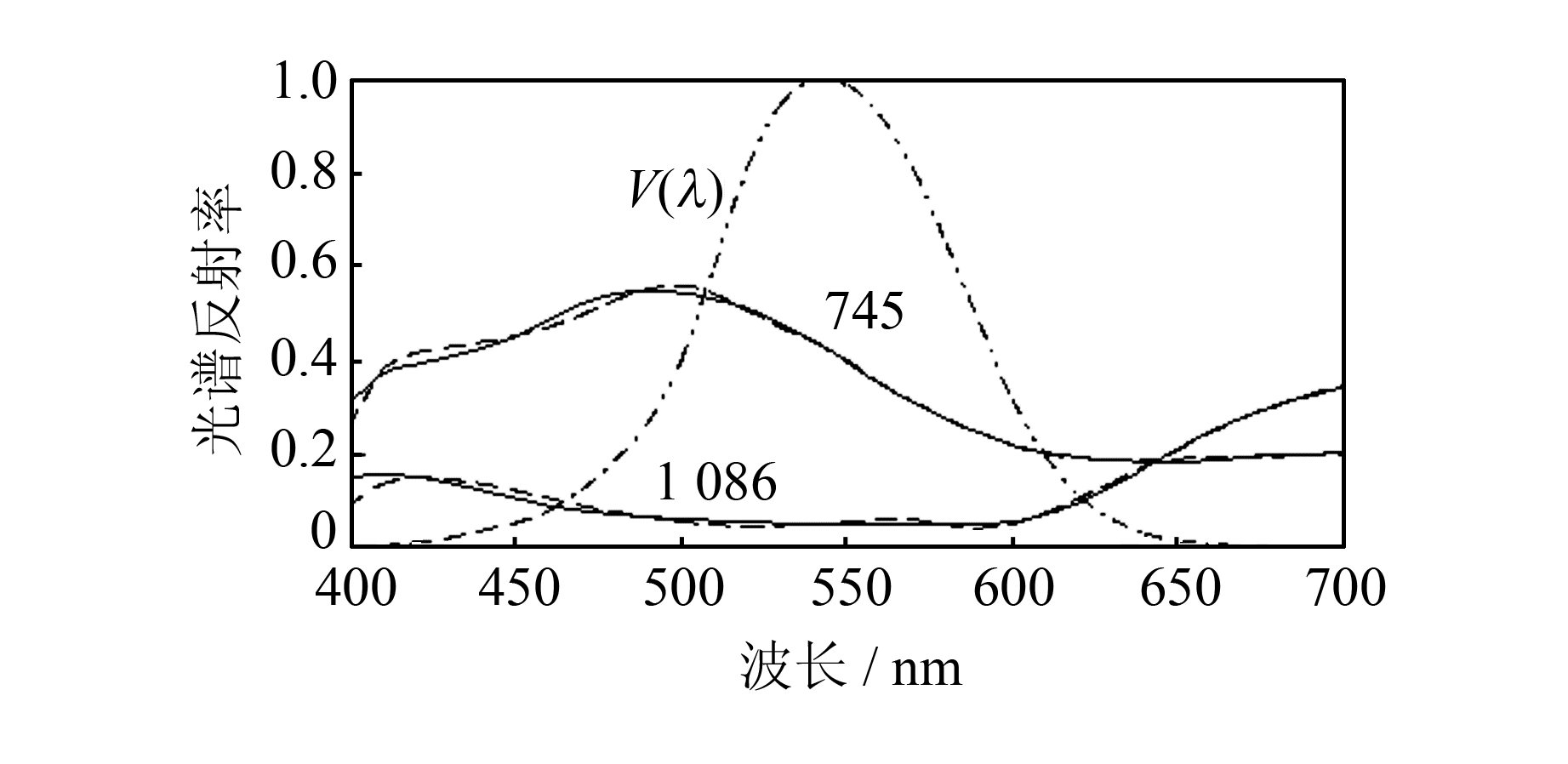
图 4使用BORSD法分别采用3、4、5、6个基向量重构同一光谱反射率(实线为原始光谱,虚线为重构光谱),前三个基向量为正交化后的对立信号A′、X′、Y′。在本文方法中仅使用三个基向量重构时,重构光谱与原始光谱有明显差异,随着残余光谱基向量的加入,光谱重构精度提高,当基向量数目达到6个时,重构光谱与原始光谱形状非常接近。
|
| 图 4 使用BORSD法重构一光谱反射率样本 Fig. 4 An Example of Reconstructing One Reflectance Spectra Using BORSD |
接着验证BORSD法相对传统PCA降维法能否有效提高光谱和色度的匹配精度,以及具有变光照情况下色度匹配的稳定性情况。表 3和表 4分别是PCA法和BORSD法在不同标准光源下使用不同数量的基向量重构Munsell色块的平均重构误差比较,图 5和图 6是比较的图表形式。从图 5、6中可以明显看出,使用BORSD法降维,当基向量只有三个时,重构误差很大,但随着残余光谱的基向量的加入,重构误差逐渐减少并下降明显,下降趋势要明显快于PCA法。当基向量数目达到6个后,再继续增加基向量,色差和光谱差的下降趋势变缓,色度精度和光谱精度的增加不再明显。与传统的PCA法相比较,当基向量数量达到6个后,光谱精度两者接近,但色度精度提高明显。在只使用三个基向量重构光谱的情况下,当光照光源为标准光源C、D50时,用A′、X′、Y′作为基向量,其色度精度明显高于直接用PCA法推导的前三个基向量。以D50光源为例,BORSD法三个基向量重构其平均色差仅为0.67,而直接用主成分分析推导的前三个基向量重构光谱的平均色差为2.85,效果明显。对于标准光源A和F11,使用三个基向量重构BORSD法虽然平均色差要大于PCA法,但在最大色差上明显减少。造成这种情况的原因在于标准光源C和D50的的光谱曲线较为平直,而标准光源A和F11的光谱曲线则不够平直,尤其是F11变化剧烈。但增加基向量到6个后,无论哪种标准光源,BORSD法的色度精度较PCA法都有明显提升。这充分证明,该方法用引入人眼视锥响应光谱灵敏度作为低维线性模型前三个基向量来表征色度信息是切实可行的。在变光照情况下,BORSD法对于光谱形状平滑的光源,色差稳定性较好。以使用6个基向量重构光谱为例,在A、C、D50光源下的平均色差分别为0.30、0.09、0.17,但对光谱形状不够平滑的F11光源,其重构光谱平均色差为1.05,与其他光照光源有一定差距。
|
基向量 数目 | CIELAB ΔEab*(2。 ,标准观察者) | sRMS | |||
| A | C | D50 | F11 | ||
| 3 | 2.32 | 2.93 | 2.85 | 3.62 | 0.020 3 |
| 4 | 2.00 | 1.80 | 1.98 | 3.40 | 0.014 9 |
| 5 | 0.85 | 0.96 | 0.89 | 1.43 | 0.011 7 |
| 6 | 0.77 | 0.94 | 0.88 | 1.23 | 0.010 2 |
| 7 | 0.19 | 0.20 | 0.17 | 0.78 | 0.007 0 |
| 8 | 0.15 | 0.13 | 0.13 | 0.65 | 0.006 2 |
| 9 | 0.11 | 0.13 | 0.13 | 0.59 | 0.003 5 |
| 基向量数目 | CIELAB ΔEab*(2。 ,标准观察者) | sRMS | |||
| A | C | D50 | F11 | ||
| 3 | 7.35 | 1.84 | 0.67 | 4.05 | 0.153 8 |
| 4 | 1.70 | 0.69 | 0.47 | 4.49 | 0.035 6 |
| 5 | 0.95 | 0.24 | 0.42 | 2.05 | 0.015 8 |
| 6 | 0.30 | 0.09 | 0.17 | 1.05 | 0.009 7 |
| 7 | 0.17 | 0.08 | 0.15 | 0.75 | 0.007 7 |
| 8 | 0.15 | 0.08 | 0.12 | 0.68 | 0.006 9 |
| 9 | 0.08 | 0.07 | 0.07 | 0.64 | 0.006 1 |
|
| 图 5 PCA法与BORSD法使用不同数量的基向量重构Munsell色块平均光谱均方根误差比较 Fig. 5 Comparisons of Average sRMS for Munsell Samples Using PCA and BORSD |
|
| 图 6 PCA法与BORSD法使用不同数量的基向量重构Munsell色块平均色差比较 Fig. 6 Comparisons of Average CIELAB ΔE*ab for Different Number of Basis Functions Reconstructed Munsell Samples Using PCA and BORSD |
通过以上实验可以看出,传统的基于主成分分析的光谱降维方法并不适用于面向颜色复制的光谱降维。要获得好的光谱图像降维效果,降维数据与原始光谱数据相比,需要在色度、光谱以及光照变换的色差稳定性三方面都有好的表现。本文提出的BORSD法构建了一个6维线性模型,前三个基向量用基于人眼视觉机理的三个对立信号构建来表征色度信息,模型的后三个基向量由残余光谱的主成分分析推导,来增加光谱精度。这样,就将人眼视觉机理与传统的主成分分析相结合,可在不降低模型光谱重构精度的情况下有效提高降维光谱的色度精度和变光照下的色差稳定性。
| [1] | Rosen M, Imai F, Jiang W, et al. Spectral Reproduction from Scene to Hardcopy Ⅱ: Image Processing[J].SPIE, 2001, 4 300:33-41 |
| [2] | Kong Lingwang, Zhu Yuanhong, Li Qiong. Modified Multi-spectral Space for Color Representation Based on Hybrid Algorithm[J]. Geomatics and Information Science of Wuhan University, 2006, 31(9):788-798(孔令罔, 朱元泓, 李琼. 以混合算法建立宽带多光谱色彩表示空间[J]. 武汉大学学报·信息科学版, 2006, 31(9):788-798) |
| [3] | Wang Ying, Zeng Ping, Wang Yifeng. Spectral-Based Color Separation for Multi-spectral Images[J]. Acta Optica Sinica, 2009, 29 (8):2 122-2 127(王莹, 曾平, 王义峰.一种面向多光谱图像的打印分色方法[J].光学学报, 2009, 29(8):2 122-2 127) |
| [4] | Fairman H S, Brill M H. The Principal Components of Reflectances[J]. Color Research and Application, 2004, 29(2):104-110 |
| [5] | Tsutsumi S, Rosen M R, Berns R S. Spectral Color Management Using Interim Conncction Spaces Based on Spectral Decomposition[J]. Color Research and Application, 2008, 33(4):282-299 |
| [6] | JolliffeI T. Principal Component Analysis[M]. NewYork: Springer-Verlag, 1986 |
| [7] | Gao Yang, Wang Xuesong, Cheng Yuhu. Dimensionality Reduction of Hyperspectral Data Using Non-negative Sparsity Graph[J]. Journal of Electronics & Information Technology, 2013, 35(5): 1 177-1 184(高阳, 王雪松, 程玉虎. 基于非负稀疏图的高光谱数据降维[J]. 电子与信息学报, 2013, 35(5):1 177-1 184) |
| [8] | Shi Q, Zhang L, Du B. Semi-Supervised Discriminative Locally Enhanced Alignment for Hyperspectral Image Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(9): 4 800-4 815 |
| [9] | Li Na, Zhao Huijie, Jia Guorui. Dimensional Reduction Method Based on Factor Analysis Model for Hyperspectral Data[J]. Journal of Image and Graphics, 2011, 16(11):2 030-2 035(李娜, 赵慧洁, 贾国瑞. 因子分析模型的高光谱数据降维方法[J]. 中国图像图形学报, 2011, 16(11):2 030-2 035) |
| [10] | Parkkinen J, Hallikainen J, Jääskelääinen T. Charateristic Spectra of Munsell Colors[J]. Journal of the Optical Society of America, 1989, 6(2): 378-322 |
| [11] | Zhu Yuanhong, Li Bo, He Songhua. Multi-channel Spectral Reconstruction of Monochrome Camera Using Theory of Basis Functions[J]. Geomatics and Information Science of Wuhan University, 2012, 37(12):1 482-1 485(朱元泓, 李博, 何颂华.使用基函数理论的单色相机多通道光谱重构[J].武汉大学学报·信息科学版, 2012, 37(12):1 482-1 485) |
| [12] | Tzeng D. Spectral-Based Color Separation Algorithm Development for Multiple Ink Color Reproduction[D]. Rochester: Rochester Institute of Technology, 1999 |
 2015, Vol. 40
2015, Vol. 40



