文章信息
- 安文, 孟祥伟
- AN Wen, MENG Xiangwei
- 一种改进的杂波图检测方法
- An Improved Clutter Map Detection Method
- 武汉大学学报·信息科学版, 2015, 40(9): 1176-1179
- Geomatics and Information Science of Wuhan University, 2015, 40(9): 1176-1179
- http://dx.doi.org/10.13203/j.whugis20140449
-
文章历史
- 收稿日期: 2014-06-10
2. 海军航空工程学院电子信息工程系, 山东 烟台, 264001
2. Department of Electronic and Information Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China
雷达常在非高斯、非平稳的杂波环境中检测目标,若采用固定门限进行检测会产生过量虚警,将导致后续的数据处理装置过载或无法提取有用目标信息,因而,对雷达目标进行检测常采用恒虚警率(CFAR)处理技术。实现雷达目标恒虚警率检测的方法按杂波强度估计方式的不同可分为两大类:(1) 利用检测单元附近(距离或多谱勒)的参考单元样本进行杂波强度估计的滑窗式快门限CFAR检测方法。这类方法适用于在空域上较平稳的杂波背景中,其典型代表为单元平均(CA)[1]、最大选择(GO)[2]、有序统计(OS)[3]等,这些方法也在高频地波雷达对超视距舰船目标的检测[4]、SAR图像舰船或飞机目标的检测中[5]得到应用。当空域杂波强度变化剧烈时,这类方法的恒虚警损失较大且虚警概率不易保持恒定[6, 7]。(2) 杂波图检测方法,它对检测单元以往多次扫描的回波进行迭代来获得杂波强度的估计。文献[8]提出和分析了这种方法在高斯背景中的性能,在文献中常被称为Nitzberg杂波图方法。杂波图检测方法利用的是雷达杂波环境时域的相对平稳性,因此,杂波图处理不易受诸如地杂波或陆海交界处杂波非平稳性的影响。但是,经典的Nitzberg杂波图在拖尾很重的杂波环境中检测性能会恶化。针对雷达的非高斯、非平稳杂波环境,文献[9]提出了一种双模式双参数杂波图检测技术,它假定雷达杂波经过非相参积累后近似服从高斯分布,从而估计杂波的均值和方差来设置检测门限。为改善杂波图检测方法在非高斯背景中的检测性能,本文基于非相干积累提出了一种新的杂波图检测方法,并利用解析方法和重要采样技术对其在韦布尔分布杂波中的检测性能进行了分析。
1 基于非相干积累的杂波图检测方法基于非相干积累的杂波图检测方法的原理见图 1,雷达的回波信号经过平方率检波得到回波包络信号qi(n),它按照边扫描边估计的方法来进行杂波强度估计的更新。假定雷达在扫描过程中沿某一方向发射了M个探测脉冲,首先对来自某一雷达距离分辨单元的M个回波脉冲回波信号qi(n)进行非相干积累:
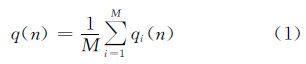
式中,qi(n)(i=1,…,M)表示在第n次扫描过程中来自某个距离分辨单元第i个脉冲的回波信号;q(n)表示脉冲积累的结果。然后,q(n)乘以一个加权因子α并加上前一次杂波背景强度的估计值p(n-1)的(1-α)倍,得到当前杂波背景强度新的估计值p(n):

|
| 图 1 基于非相干积累的杂波图检测方法的原理图 Fig. 1 Diagram of the Clutter Map Detection Method Based on Non-coherent Integration |
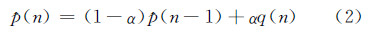
显然,式(2)是一个一阶自回归(AR)数字滤波器,它对每个距离分辨单元以往脉冲回波信号的积累结果进行指数平滑处理。加权因子α控制着衰减速率。对某个距离分辨单元的M个回波脉冲信号来说,将杂波强度的估计值p(n-1)与一个门限因子T相乘得到一个检测门限T·p(n-1),对M个脉冲中的每个回波信号qi(n)(i=1,…,M),则做出一个关于第i个脉冲信号的判决:
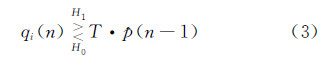
若qi(n)大于T·p(n-1),则认为第i个脉冲探测到了目标信号。但是,检测单元中是否存在目标取决于(M个脉冲信号的检测结果。本文采用二进制积累准则对于(M个脉冲信号的判决结果进行非相干积累,即如果(M个脉冲信号中至少有(K个脉冲探测到了目标,则判定在该距离单元中存在目标。
2 数学模型和数值分析结果假定雷达杂波背景服从韦布尔分布,且来自每个距离分辨单元的回波信号在脉冲之间和扫描之间统计独立,经平方律检波后杂波样本qi(n)(i=1,…,M)的概率密度函数(PDF)f(t)和累积分布函数(CDF)F(t)分别为[10, 11]:
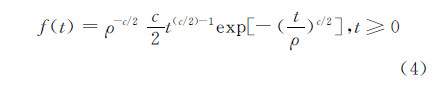
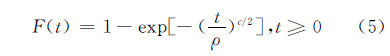
式中,(ρ和c分别代表韦布尔分布的尺度参数和形状参数。在c=2.0(相应于瑞利分布)情况下,q(n)的概率密度函数f′(t)表示为:
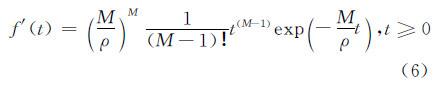
它的矩产生函数(MGF)Φq(n)(s)表示为:
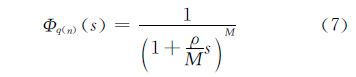
式(2)表示的是一个线性时不变(LTI)离散时间动态系统,杂波背景强度的估计可表示为系统的脉冲响应和雷达回波信号q(n)的卷积和,有:
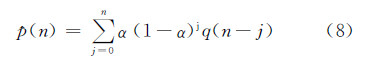
在(H1假设下和c=2.0时,假定目标模型为Swerling Ⅱ型,检测单元的回波信号qi(n)(i=1,…,M)的PDF按式(9)给出:
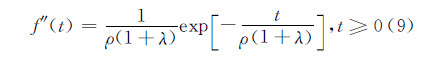
式中,λ是目标信号的信杂比(SCR)。单个脉冲信号qi(n)(i=1,…,M)的检测概率为:
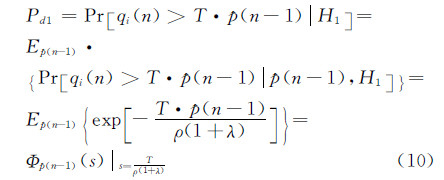
式中,Φp(n-1)(s)是杂波强度估计p(n-1)的矩产生函数;Pr[]表示求概率。因为统计独立随机变量之和的矩产生函数等于它们各自矩产生函数的乘积,故p(n-1)的MGF可表示为:
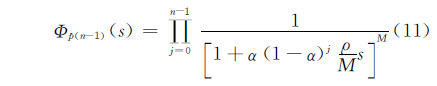
对于(M个脉冲的回波信号qi(n)(i=1,…,M)基于式(3)的判决结果进行积累,若至少有(K个脉冲探测到了目标(记为K/M),则认为在该距离单元中存在目标,改进的杂波图检测方法的总体检测概率Pd为:
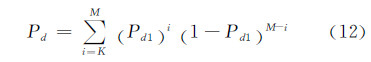
令式(10)中λ=0,则可得到单个脉冲的虚警概率Pfa1为:
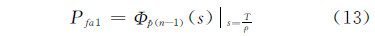
相应地,改进的杂波图检测方法的总体虚警概率Pfa为:
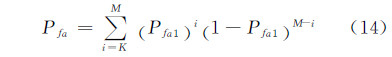
对于c≠2.0的一般情形,由于不存在统计独立的韦布尔分布随机变量之和的PDF精确表达式,故不能对其进行解析分析,本文将采用重要采样技术对其进行性能分析。
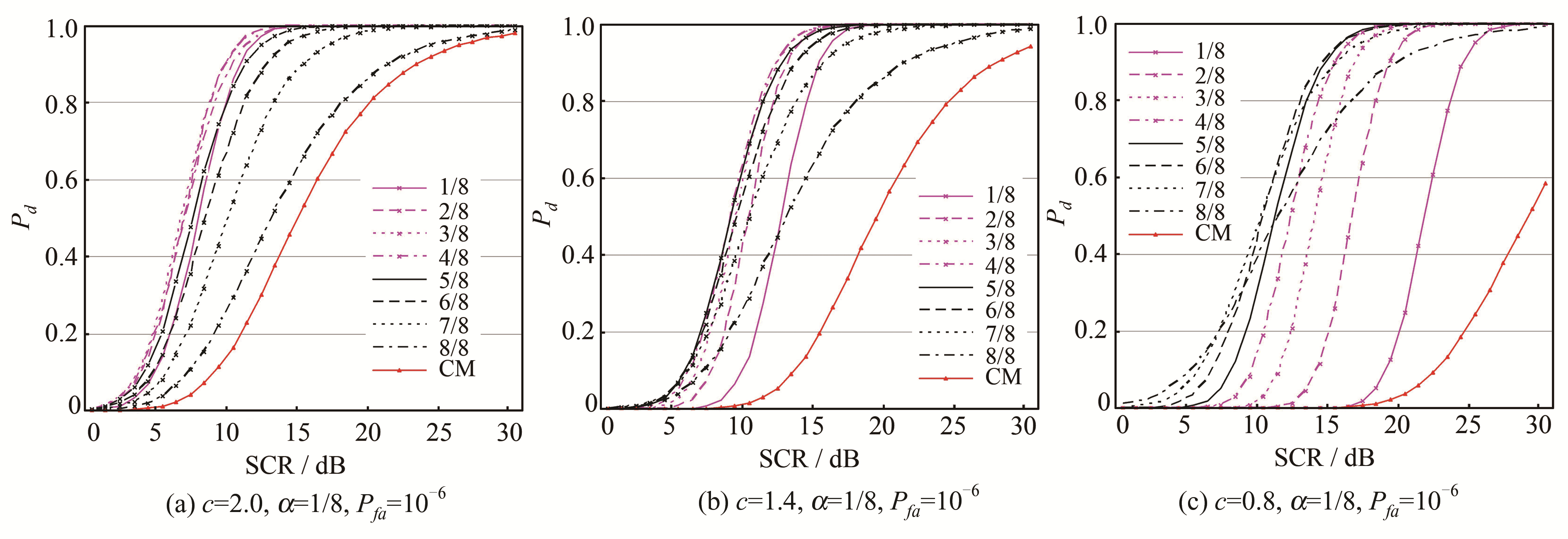
对检测器给定的虚警概率Pfa,检测门限T由式(13)、(14)来确定,它取决于杂波的形状参数c和采用的二进制积累准则(K/M)。图 2分别给出了c=2.0、c=1.4和c=0.8时,基于非相干积累的杂波图检测方法的检测概率随信杂比(SCR)的变化曲线,加权因子取α=1/8[8],虚警概率设定为Pfa=10-6。图 2中的标注“1/8”、“1/8”、…、“8/8”分别对应不同的二进制积累情况。作为比较,图 2中也给出了经典的Nitzberg杂波图的检测性能曲线,标注为“CM”。在c=2.0(相应于瑞利分布)和Pd=0.8时,从图 2(a)中可看出最佳的检测性能由二进制积累准则(2/8)获得,二进制积累(2/8)、(3/8)、(4/8)检测性能较为接近,最差的检测性能由二进制积累(8/8)获得。但是,它们均比经典的Nitzberg杂波图检测方式“CM”有较大提高。在c=1.4时,从图 2(b)中可看出最佳的检测性能由积累准则(4/8)获得,二进制积累(3/8)、(4/8)、(5/8)检测性能较为接近。在c=0.8时,从图 2(c)中可看出最佳的检测性能由积累准则(6/8)获得,最差的检测性能由二进制积累(1/8)获得。可见,对于采用8个积累脉冲的杂波图检测来说,不同积累准则方法间的差别较大,但是,它们相比经典的Nitzberg杂波图的检测性能都有较大的改善,其实质在于本文方法采用了二进制非相干积累方式,使得杂波图的检测性能得到较大提高,能够满足杂波图检测技术在实际应用中的性能需求。可以看出,对于杂波形状参数c较小也就是杂波分布的拖尾越重的情况,应该采用较高二进制积累门限K(K/M)来抑制较“尖锐”的杂波,从而获得较好的雷达目标检测性能。值得指出的是,本文中假定杂波的形状参数是已知的,在实际中可采取最大似然估计方法进行估计[12]。
|
| 图 2 基于非相干积累的杂波图检测方法的检测性能 Fig. 2 Detection Performance of the Clutter Map Based on Non-coherent Integration |
为了改善Nitzberg杂波图检测技术的检测性能,本文基于非相干积累提出了一种新的杂波图检测方法。该方法首先将M个脉冲回波进行非相干积累,对每个距离分辨单元以往的积累结果进行平滑迭代以得到杂波强度的估计,若M个回波脉冲中至少有K个脉冲探测到了目标,则判为在该距离单元中存在目标。本文采用解析方法和重要采样技术分析了这种方法的检测性能,显示出这种方法相比经典的Nitzberg杂波图检测方法的性能有较大改善,如Pfa=10-6、c=0.8时,为达到Pd=0.5的检测概率,经典的Nitzberg杂波图检测方法需要约30 dB的信杂比,而本文提出方法为达到此检测概率仅需要约10 dB。这意味着基于非相干积累的杂波图检测方法在较“尖锐”的杂波环境中仍可采用,且这种方法便于工程实现。分析结果表明,在雷达杂波形状参数c较小时,也就是杂波分布的拖尾较重的情况下,应该采用较高二进制积累门限K(K/M)进行积累来抑制较“尖锐”的杂波,从而获得较好的雷达目标检测性能。
| [1] | Finn H M, Johnson R S. Adaptive Detection Mode with Threshold Control as a Function of Spatial Sampled Clutter Level Estimates[J]. RCA Review, 1968, 29(3):414-464 |
| [2] | Hansen V G. Constant False Alarm Rate Processing in Search Radars[C]. The IEEE International Radar Conference, London, 1973 |
| [3] | Rohling H. Radar CFAR Thresholding in Clutter and Multiple Target Situations[J]. IEEE Trans Aerospace Electron Syst, 1983, 19(4):608-621 |
| [4] | Gui Renzhou. Detecting Target Located in Nonstationary Background Based on Two Dimensions Constant False Alarm Rate[J]. Geomatics and Information Science of Wuhan University, 2012, 37(3):354-357(桂任舟. 利用二维恒虚警进行非均匀噪声[J]. 武汉大学学报·信息科学版, 2012, 37(3):354-357) |
| [5] | He Chu, Zhang Yu, Liao Ziqian, et al. Compressive Sensing Based on CFAR Target Detection Algorithm for SAR Image[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7):878-882 (何楚, 张宇, 廖紫纤, 等. 基于压缩感知的SAR图像CFAR目标检测算法[J]. 武汉大学学报·信息科学版, 2014, 39(7):878-882) |
| [6] | Pourmottaghi A, Taban M R, Gazor S A. CFAR Detector in a Nonhomogenous Weibull Clutter[J]. IEEE Trans Aerospace Electron Syst, 2012, 48(2): 1 747-1 758 |
| [7] | Kronauge M, Rohling H. Fast Two-Dimensional CFAR Procedure[J]. IEEE Trans Aerospace Electron Syst, 2013, 49(3): 1 817-1 823 |
| [8] | Nitzberg R. Clutter Map CFAR analysis[J]. IEEE Trans Aerospace Electron Syst, 1986, 22(4):419-421 |
| [9] | Lin Yan, Peng Yingning, Wang Xiutan, et al. Implementation of a Dual Mode Biparametric Clutter-Map CFAR Detector[J]. Systems Engineering and Electronics, 2003, 25(2): 133-136 (林彦, 彭应宁, 王秀坛, 等. 一种双模式双参数杂波图恒虚警检测器的实现[J]. 系统工程与电子技术, 2003, 25(2): 133-136) |
| [10] | Meng Xiangwei. Performance Analysis of OS-CFAR with Binary Integration for Weibull Background[J]. IEEE Trans Aerospace Electron Sys, 2013, 49(2): 1 357-1 366 |
| [11] | Meng Xiangwei. Performance Analysis of Ordered Statistic Greatest of Constant False Alarm Rate With Binary Integration for M sweeps[J]. IET Radar, Sonar and Navigation, 2010, 4(1): 37-48 |
| [12] | He You, Guan Jian, Meng Xiangwei. Radar Target Detection and CFAR Processing[M]. Beijing: Tsinghua University Press, 2011(何友, 关键, 孟祥伟. 雷达目标检测与恒虚警处理(第二版)[M]. 北京:清华大学出版社, 2011) |
 2015, Vol. 40
2015, Vol. 40


