文章信息
- 孙伟伟, 刘春, 李巍岳
- SUN Weiwei, LIU Chun, LI Weiyue
- 联合改进拉普拉斯特征映射和k-近邻分类器的高光谱影像分类
- Hyperspectral Imagery Classification Using the Combination of Improved Laplacian Eigenmaps and Improved k-nearest Neighbor Classifier
- 武汉大学学报·信息科学版, 2015, 40(9): 1151-1156
- Geomatics and Information Science of Wuhan University, 2015, 40(9): 1151-1156
- http://dx.doi.org/10.13203/j.whugis20130654
-
文章历史
- 收稿日期:2013-11-07
2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉, 430079;
3. 同济大学测绘与地理信息学院, 上海, 200092;
4. 现代工程测量国家测绘地理信息局重点实验室, 上海, 200092;
5. 上海师范大学城市发展研究院, 上海, 200234;
6. 矿山空间信息技术国家测绘地理信息局重点实验室, 河南 焦作, 454000
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
3. College of Surveying and Geo-informatics, Tongji University, Shanghai 200092, China;
4. Key Laboratory of Advanced Engineering Survey of NASMG, Shanghai 200092, China;
5. Institute of City Development Research, Shanghai Normal University, Shanghai 200234, China;
6. Key Laboratory of Mining Spatial Information Technology of NASMG, Jiaozuo 454000, China
高光谱影像能够获得地物数十至数百个波段的光谱信息,其分类结果对后续的植被覆盖制图[1]和地质探测[2]等应用意义重大。但是,高光谱影像光谱波段众多且相关性强,存在严重的“维数灾难”现象[3],需要庞大的训练样本来保证较高分类精度,这对训练样本采集产生了巨大压力。因此,高光谱影像在用于土地覆盖分类应用时,可以将高光谱影像先进行降维以减少原始数据的波段数,然后选择分类器来实现分类。
由于二次反射、像元内部异质等因素影响,高光谱影像存在明显的非线性特征[4]。近年来,学者们开始引入非线性流形学习方法来降维高光谱影像然后实现分类。目前,存在许多非线性流形学习方法,如等距映射(isometric mapping,Isomap)[5]、局部线性嵌入[6]和拉普拉斯特征映射(Laplacian eigenmaps,LE)[7]等。利用流形学习方法降维高光谱影像的研究已取得一定成果[8, 9, 10, 11]。高光谱影像具有“图谱合一”特性,图像中任意像素的光谱向量具有空间特性。特别地,由于受到不同地形、不同光照及空间分辨率的影响,影像中同类地物的光谱特性随空间位置而变化。常规流形学习方法没有考虑影像的空间特征,这将降低降维结果的准确性。
流形学习降维后需要利用分类器来实现嵌入结果的分类,如采用k-近邻法(k-nearest neighbors,KNN)和支持向量机法(support vector machine,SVM)等。文献[12]利用KNN分类器研究Isomap降维用于高光谱影像的分类性能。文献[13]提出监督局部流形学习降维高光谱影像,并利用SVM分类器法来分类嵌入结果。高光谱影像流形学习降维后,各地物像素点对应的流形坐标向量具有空间位置特征,同类地物的流形坐标向量随着空间位置的不同产生变异。因此应考虑流形坐标向量的空间特征,更好满足高光谱影像的分类要求。
LE方法是流形学习局部方法的典型代表,其计算速度快,能够保持局部的邻域结构在降维前后保持不变;而分类器中KNN方法最常用,因其计算速度快、参数设置简单。因此,本文以LE方法和KNN分类器组合为例,提出自适应加权综合核距离度量来同时改进流形学习和分类器,得到改进LE (improved LE,ILE)降维和改进KNN(improved KNN,IKNN)分类器的组合策略,解决高光谱影像流形学习降维和低维流形坐标分类中忽略了影像空间特征的问题。
1 高光谱影像LE降维LE算法认为高维空间中距离很近的点投影到低维流形上也应距离很近[7]。流形结构采用邻域图的加权拉普拉斯核来逼近拉普拉斯-贝尔特拉米算子,并通过映射来保持局部邻域的一些特性。假设高光谱数据为二维矩阵X=[x1 … xi … xN]T∈RD,每一列向量xi对应高光谱影像中一个像素点,N和D分别为像素点总数和波段总数;假设LE流形坐标Y=[y1 … yN]T∈Rd,其中d为流形坐标的维数;假设每个像素点在高维空间与周围像素点构成k1-邻域,其中k1为邻域大小,LE降维可分为三个步骤:
1) 利用像素点i和j的欧氏距离构建邻域。如果j是i的最近的k1个点中的一个时,两者相邻存在有向边,且边长为两者间的欧氏距离;否则,两者距离为0。
2) 计算像素点i和j之间的权重系数,得到权重矩阵W。当像素点i和j离得很近的时候,LE用一个正的权wij来联系这两个样本点。如果i和j位于同一邻域,两像素点间的权重系数wij=exp(-‖xi-xj‖2/σ2,其中,σ2为径向基核函数的方差;否则,wij=0。
3) 基于图谱理论计算嵌入坐标Y。假设Φ表示对角元素φii=∑jwij的对角矩阵,yi通过极小化目标函数(1)而获得:
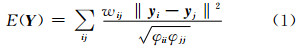
为了得到唯一流形坐标Y,对式(1)附加中心化和标准化的限制,函数(1)可变为函数(2):
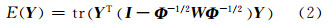
计算矩阵Δ=I-Φ-1/2WΦ-1/2的最小d+1个特征向量u1,…,ud+1,则第2~d+1个特征向量为高光谱影像LE降维的嵌入结果。
2 ILE降维和IKNN组合策略 2.1 自适应加权综合核距离度量高光谱影像中光谱特征的空间变异可通过中心像素与其空间邻域(空间窗口)内像素的关系来描述。因此,文献[14]提出采用加权综合核距离dist(i,j)来改善像素点间的相似性度量,计算公式为:
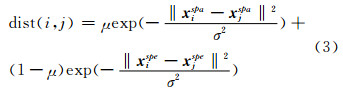
其中,μ是平衡因子且0<μ<1,调节光谱特征和空间特征的权重;xispe是像素i归一化的光谱向量;xspai是像素i的空间特征向量;‖·‖2是两向量间的欧氏距离平方;σ是径向基核函数的标准差。
加权综合核距离通常采用统一的空间邻域来计算像素点的空间特征向量,这容易产生一些问题。例如,像素点A和B都代表同一类地物“未耕犁的大豆地”,然而位于两类不同地物边界的像素B的空间邻域应小于位于同类地物围绕的中心像素A的空间邻域。否则,像素B的空间邻域过大则导致空间窗口包含不同类地物而影响空间特征向量的估算。本文提出自适应空间窗口来改善加权综合核距离,称为自适应加权综合核距离。
自适应空间窗口基于窗口内部像元的光谱特征差异性最小的原则,具体原理为:在以像素点i为中心的一组候选空间窗口中,内部元素间光谱向量平均变异最小的窗口即为i的所有候选窗口中的最优窗口。假设像素点i的空间窗口集合为B={bj},j=1,…,g,g为空间窗口集中候选窗口个数;假设窗口bj内光谱向量集Sj所含光谱向量个数为hj,自适应空间窗口的计算步骤如下:(1)对每一空间窗口bj,计算内部各元素的方差得到方差向量Jj=var(Sj),其中var为方差计算;(2)计算每个空间窗口的方差向量Jj的平均方差,得到方差向量R;(3)最小的二阶方差min(R)对应的窗口为最优空间窗口。空间窗口集中的最大窗口通过交叉验证设置,最小窗口设置为3×3。自适应窗口能够保证最优窗口内各像素点间的光谱特征差异最小,反映窗口内光照及地形等环境条件差异最小,能够更好地表达高光谱影像的空间特征。
2.2 高光谱影像的ILE降维高光谱影像的LE降维能够保持降维前后各像素点的k1-邻域结构基本不变。高光谱影像中,常规的欧氏距离度量并未考虑像素点对应的实际地物的光谱特性随影像中空间位置变化而产生的变异。此外,k1-邻域内像素点的权重系数也未考虑像素点的空间特征的影响。因此,本文提出了高光谱影像的ILE降维方法。首先,采用自适应加权综合核距离搜索并构建k1-邻域。其次,根据k1-邻域来确定两像素点间的权重wij。采用自适应加权综合核距离代替常规径向基核距离,改进权重wij的计算结果。如果xi和xj位于同一邻域时,改进后的权重计算为wij=dist(xi,xj);否则,wij=0。最后,通过计算矩阵Δ=I-Φ-1/2WΦ-1/2的最小d+1个特征向量u1,…,ud+1,得到2至d+1个特征向量为ILE降维的嵌入结果。
2.3 高光谱影像ILE流形坐标的IKNN分类KNN方法的主要思想为[15]:若一个像素点在d维嵌入空间中的k2个最相似的像素点中的大多数都属于某一个类别,则该像素点也属于这个类别。常规距离原都是量度d维空间内的各像素流形特征间的相似性,并未考虑低维流形图中流形坐标向量的空间特征。本文利用自适应加权综合核距离来改进KNN分类器。假设降维后流形坐标为Y=[y1 … yN]T∈Rd,Y=Ytr∪Yte,其中,训练样本为Ytr=[ytr11 … ytrpc … ytrmC]T,测试样本集为Yte=[yte1 … yteq … yten]T,C为实际地物的类别数,m和n分别为训练样本和测试样本中流形坐标向量的个数且N=m+n。IKNN的分类过程为:首先对每一个待测试向量yteq,利用自适应加权综合核距离计算得到每个待测试坐标向量yteq在C个已知类别的训练样本集中的k2-邻域Yq=[yq1 … yqt yqk2]T。其次,计算k2-邻域内ILE坐标向量对应的类别标签Lq=[lq1 … lqt … lqk2]。最后,投票选举k2-邻域内频率最大的类别为yteq的类别标签:
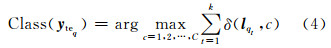
其中,δ为克罗内克函数。
2.4 ILE降维和IKNN组合策略的分类流程ILE降维和IKNN组合策略的高光谱影像分类流程见图 1。
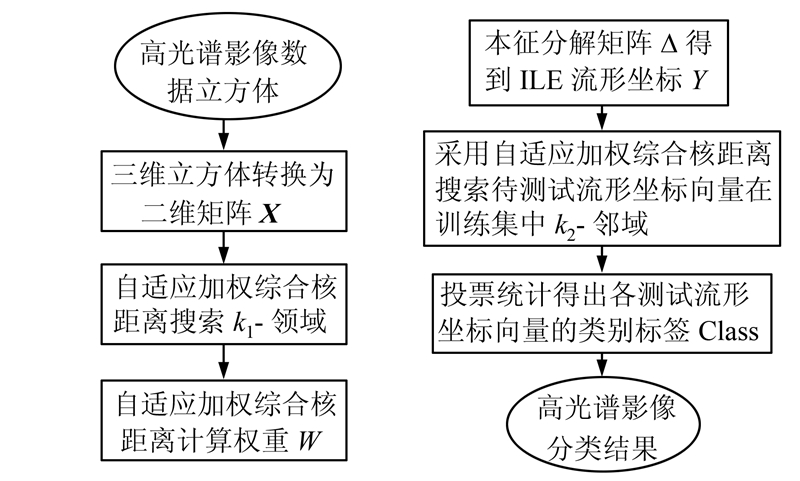
|
| 图 1 ILE和IKNN组合策略高光谱影像分类 Fig. 1 Hyperspectral Image Classification with Combination Scheme of ILE and IKNN |
1) 采用式(3)计算任意像素点i和j间的自适应加权综合核距离来构建k1-邻域。
2) 通过式(3)自适应加权综合核距离计算各像素点i和j间的权重。
3) 通过本征分解式(2)中矩阵Δ得到ILE流形坐标Y。
4) 采用式(3)计算每个待测试流形坐标向量在训练样本中的k2-邻域Yq。
5) 利用式(4)得到测试流形坐标向量的类别标签Class。
3 实验结果与分析 3.1 实验数据描述Indian数据由美国JPL成像光谱仪于1992-06-12采集得到,波段数为200,空间分辨率为20 m,光谱分辨率为10 nm,光谱区间为200 nm~2 400 nm。图 2为覆盖西拉法叶地区西部的一块区域,包含145像素×145像素,16类主要地物。PaviaU影像由ROSIS传感器采集得到,覆盖帕维亚大学区域,共有103个波段,光谱区间为430 nm~860 nm,光谱分辨率为2.5 nm,空间分辨率为1.3 m,如图 3所示。影像包含350像素×340像素,共9类地物(包括阴影)。

|
| 图 2 Indian数据 Fig. 2 Indian Datasets |

|
| 图 3 PaviaU数据 Fig. 3 PaviaU Datasets |
实验利用以上两组高光谱影像数据来验证ILE-IKNN组合策略的分类性能。实验采用总体分类精度(overall classification accuracy,OCA)和平均分类精度(average classification accuracy,ACA)来定量评价分类结果;同时,采用用户精度来评价得到的每一类地物的分类结果。
3.2.1 Indian数据LE和ILE降维方法中,邻域大小k1设置为15,嵌入维数大小d为65。图 4(a)列出了4种组合策略得到的Indian中各地物分类结果的用户精度。图 5列出了Indian数据中4种组合策略得到的分类图,图例中每个序号对应一类地物,第0类是未参与分类的其他地物。表 1给出了4种组合策略分类结果的平均和总体分类精度。ILE-IKNN得到的分类结果的总体和平均精度最高,分别为87.80%和84.30%。其大多数单一地物的分类精度也明显高于LE-KNN策略,尤其第1类(苜蓿)、第4类(玉米地)、第9类(燕麦)和第12类(耕作玉米地)的分类精度增幅最为明显。ILE-KNN的分类精度以及大多数单一地物的分类精度高于LE-KNN,总体精度和平均精度分别高22.9%和19.07%。LE-IKNN的总体和平均分类精度分别比LE-KNN高约18.75%和14.63%。ILE-KNN的分类精度稍优于LE-IKNN,LE-KNN的分类精度最低。
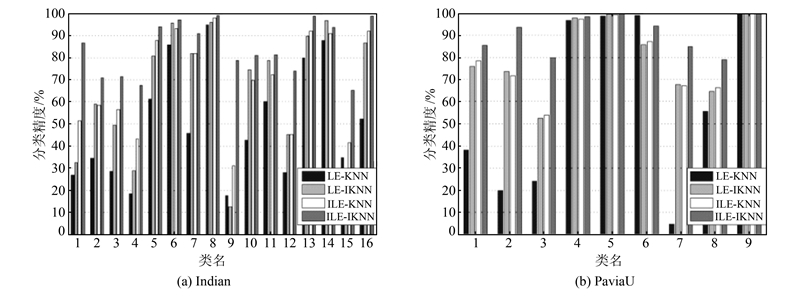
|
| 图 4 数据中4种组合策略的单一地物分类精度 Fig. 4 Classification Accuracy of Ground Objects from Four Combination Schemes |

|
| 图 5 Indian数据中4种组合策略的分类图 Fig. 5 Classification Maps from Four Combination Schemes on Indian Dataset |
| 数据集 | 分类精度 | 4种LE降维和KNN分类组合策略 | |||
| ILE-IKNN | ILE-KNN | LE-IKNN | LE-KNN | ||
| Indian数据 | OCA | 87.80±0.020 | 76.53±0.043 | 72.38±0.037 | 53.63±0.042 |
| ACA | 84.30±0.031 | 69.03±0.039 | 64.59±0.040 | 49.96±0.059 | |
| PaviaU数据 | OCA | 93.71±0.029 | 83.04±0.042 | 79.77±0.033 | 62.14±0.046 |
| ACA | 90.66±0.027 | 80.13±0.035 | 78.24±0.050 | 59.64±0.061 | |
LE和ILE降维过程中邻域大小k1设定为20,嵌入维数大小d为25。图 4(b)列出了PaviaU数据中4种组合策略得到的各地物分类结果的用户精度。表 1量化给出了PaviaU数据中4种组合策略得到的分类精度。图 6列出了4种组合策略得到的分类图,图例中每个序号对应一类地物。ILE-IKNN得到的分类精度最高,总体精度和平均精度超过LE-KNN分别约31.57%和31.02%。ILE-IKNN中单一地物的分类精度也明显高于LE-KNN,尤其第2类(牧场)、第3类(碎石)和第7类(沥青)的分类优势最为明显。ILE-KNN的总体和平均分类精度高于LE-KNN 20.9%和20.49%,而且大多数地物的分类精度也优于LE-KNN。LE-IKNN的分类精度高于LE-KNN,平均高约18%。LE-KNN的分类精度最低,仅60%左右,其中第2类(牧场)、第3类(碎石)和第7类(沥青)的识别精度最低,部分原因是地物本身较难和其他地物进行区分。此外,ILE-KNN的总体和平均分类精度稍高于LE-IKNN。

|
| 图 6 PaviaU数据中4种组合策略的分类图 Fig. 6 Classification Maps from Four Combination Schemes on PaviaU Dataset |
本文提出联合改进LE降维和改进KNN分类器的组合策略(ILE-IKNN)来提高常规LE降维和KNN分类的分类精度,通过Indian和PaviaU两个高光谱数据集,对比其他三种组合策略(LE-IKNN、ILE-KNN和LE-KNN)来验证ILE-IKNN组合策略的有效性。结果证明,ILE-IKNN能够大幅度提升LE-KNN策略的分类精度,而且大多数单一地物的分类精度都有显著提升。但是,还需对ILE-IKNN组合策略中相关参数配置作进一步分析,如平衡因子μ和IKNN分类器中邻域大小k2。同时,未来将定量分析不同环境因素对高光谱影像中不同位置的同类地物的光谱特性变异产生的影响,以更好完善本文提出的方法。
| [1] | Zhang C, Xie Z. Combining Object-Based Texture Measures with a Neural Network for Vegetation Mapping in the Everglades from Hyperspectral Imagery[J]. Remote Sensing of Environment, 2012, 124: 310-320 |
| [2] | Bishop C A, Liu J G, Mason P J.Hyperspectral Remote Sensing for Mineral Exploration in Pulang, Yunnan Province, China[J]. International Journal of Remote Sensing, 2011, 32:2 409-2 426 |
| [3] | Donoho D L. High-Dimensional Data Analysis: The Curses and Blessings of Dimensionality[C]. AMS Math Challenges Lecture, Los Angeles, 2000 |
| [4] | Bachmann C M, Ainsworth T L, Fusina R A. Exploiting Manifold Geometry in Hyperspectral Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43:441-454 |
| [5] | Tenenbaum J B, Silva V, Langford J C. A Global Geometric Framework for Nonlinear Dimensionality Reduction[J]. Science, 2000,290: 2 319-2 323 |
| [6] | Roweis S T, Saul L K. Nonlinear Dimensionality Reduction by Locally Linear Embedding[J]. Science, 2000, 290: 2 323-2 326 |
| [7] | Belkin M, Niyogi P. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation[J]. Neural Computation, 2003,15:1 373-1 396 |
| [8] | Qian S E, Chen G. A New Nonlinear Dimensionality Reduction Method with Application to Hyperspectral Image Analysis[C]. IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain,2007 |
| [9] | Crawford M M, Ma L, Kin W. Exploring Nonlinear Manifold Learning for Classification of Hyperspectral Data[J]. Optical Remote Sensing, 2011(3): 207-234 |
| [10] | Sun Weiwei, Liu Chun, Shi Beiqi, et al. Manifold Coordinate Repairing of Lost Points with PLS for Isomap Nonlinear Dimensionality Reduction of Hyperspectral Image[J]. Geomatics and Information Science of Wuhan University, 2012, 37(5):550-554(孙伟伟, 刘春, 施蓓琦, 等. 利用偏最小二乘方法修复高光谱影像等距映射降维中遗失点的坐标[J]. 武汉大学学报·信息科学版, 2012, 37(5): 550-554) |
| [11] | Li Aixia, Guan Zequn, Feng Tiantian. A Novel Method on Manifold for Multi-Image Matching[J]. Geomatics and Information Science of Wuhan University, 2012, 37(11):1 303-1 306(李爱霞, 关泽群, 冯甜甜. 一种利用流形学习进行多影像匹配的方法[J]. 武汉大学学报·信息科学版, 2012, 37(11): 1 303-1 306) |
| [12] | Chen Y, Crawford M, Ghosh J. Applying Nonlinear Manifold Learning to Hyperspectral Data for Land Cover Classification[C]. IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 2005 |
| [13] | Ma L, Crawford M M, Tian J. Local Manifold Learning-Based k-Nearest Neighbor for Hyperspectral Image Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010,48: 4 099-4 109 |
| [14] | Camps-Valls G, Gomez-Chova L, Munoz-Mari J, et al. Composite Kernels for Hyperspectral Image Classification[J]. IEEE Geoscience and Remote Sensing Letters, 2006(3):93-97 |
| [15] | Cover T, Hart P. Nearest Neighbor Pattern Classification[J]. IEEE Transactions on Information Theory, 1967, 13:21-27 |
 2015, Vol. 40
2015, Vol. 40



