文章信息
- 黄远程, 钟燕飞, 赵野鹤, 朱卫恒
- HUANG Yuancheng, ZHONG Yanfei, ZHAO Yehe, ZHU Weiheng
- 联合盲分解与稀疏表达的高光谱图像异常目标检测
- Joint Blind Unmixing and Sparse Representation for Anomaly Detection in Hyperspectral Image
- 武汉大学学报·信息科学版, 2015, 40(9): 1144-1150
- Geomatics and Information Science of Wuhan University, 2015, 40(9): 1144-1150
- http://dx.doi.org/10.13203/j.whugis20140575
-
文章历史
- 收稿日期:2014-07-28
2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉, 430079
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
异常目标是高光谱遥感信息提取的重要内容,它通常预示着不寻常事件的发生,从全局角度而言,它是影像中的小概率事件;从局部角度而言,它的光谱或空间分布机制异于背景样本[1]。本文针对高光谱影像中的异常目标进行检测,这是一种感兴趣目标先验信息缺失的检测问题。对此,文献[2]在背景为多元高斯分布的假设前提下提出了经典的RX算子,文献[3]提出了非线性空间下的核RX算子,文献[4]通过计算检验样本与不同聚类之间的距离进行异常提取,从一定程度减弱了对高斯分布假设的依赖。然而,由于实际地物的复杂性,背景的多元高斯分布假设往往很难满足。因此,一种不依赖于背景高斯分布假设的稳健异常检测方法是值得研究的。
本文利用近来广受关注的稀疏表达理论[5]进行高光谱图像异常目标检测。稀疏表达理论把测试样本表示为由训练样本构成的超完备结构性字典中基原子的稀疏线性组合,充分利用了训练样本的全体上下文信息,其稀疏回归系数包含的判别信息可用于分类和识别[6],并已成功应用于高光谱图像分类[7]、已知目标信息的目标探测[8]和稀疏混合像元分解[9]。但是,异常目标检测问题没有先验的目标和背景字典。鉴于稀疏表达的优势与异常探测的难点,本文以稀疏表达理论为基础,主要解决3个问题:① 在信息不充足的条件下,实现稀疏表达背景字典的非监督构造;② 依据异常目标所表现出的低概率性质,建立基于稀疏表达回归残差分析的异常检测理论;③ 将字典构造的全局性与地物的局部连续性结合,提高目标检测的精度。
1 研究方法 1.1 样本的稀疏表达假设影像中地物类的样本为A=A0,A1,…Ac,代表第i类的样本是Ai∈Rm×ni,ni是第i类的样本数目,A∈Rm×n,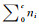 =n,m<<n;其中,A0是目标类子字典,Ai(i=1,…,c)是背景类子字典。则以训练样本A为字典对测试样本y∈Rm的表达是:
=n,m<<n;其中,A0是目标类子字典,Ai(i=1,…,c)是背景类子字典。则以训练样本A为字典对测试样本y∈Rm的表达是:

式中,x是利用A中所有原子对观测样本y联合线性编码的系数,这种联合表达起到特征互补的作用。同时依据邻近性,字典A中对测试样本相关的原子数相对少;从混合像元角度而言,构成混合像元的端元并不是影像中全部的端元类型,而是其中有限的端元的组合,因而系数x是稀疏的,对系数x的求解为:
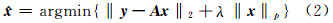
式中,等式右边第二项为正则稀疏约束项,其中L0和L1稀疏正则是最为常用的,在限制等容特性(RIP)条件下两类稀疏约束是等价的[5]。考虑到文献[10]提出的对偶增广拉格朗日(dual augmented Lagrangian methods,DALM)在大规模的稀疏表达求解中能获得较高的计算效率,故针对高光谱数据存在的大量计算,本文采用DALM方法进行L1凸优化求解系数。
在异常目标检测问题中有关于目标A0和背景的训练样本信息是未知的,因而直接稀疏表达感兴趣目标是有困难的。
1.2 基于盲分解的背景字典的建立由于异常目标相对于背景出现的概率低,而背景信息相对丰富,故可先建立背景字典,获得对背景的完整描述。从经典的线性混合分解模型可知,由端元构成的单形体能够包络整个影像空间[11, 12],即利用端元光谱能够有效表达所有的观测样本,因而如果能有效获得背景端元,就可以利用端元信息来描述背景。但不同于经典端元提取算法仅以单条端元光谱代表某地物,本文采用一束端元来表达某类地物,然后集合每类端元束构建背景字典,这样能表达地物的随机性特点,具体步骤如下。
1) 参数定义。定义三个参数:① 包含了异常地物类的影像的端元数p,若用户对此数未知则采用经验HFC算法[13]进行估计;② 每类端元在混合像元中的组分下限为low(k)(0
2) 盲分解。运用基于最小外接单形体体积原理的N-FINDR自动端元提取算法得到p条端元光谱,然后以此为基础采用包含“非负”与“和为1”约束的全限制性线性混合像元分解[14]算法对高光谱图像进行分解,完成盲分解过程得到组分图像F。
3)图像分类。对图像像元进行分类,每个像元的类别归属依据组分值最大的原则划分,即设观测像元y(i,j),(i,j)为像元坐标,Fk(i,j)表示像元y(i,j)的第k类地物组分值:

也就是像元归属于组分值最大对应的端元类。
4) 约束性背景端元束估计。在分类图像中,将占像元数比例小于a%的类归为可能的异常类,不参与构建背景字典,同时计算像元中这些类别的组分之和:
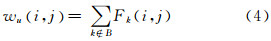
wu(i,j)关联着可能的异常特征;其他所占像元数比例大于或等于a%的类属于背景类,记为类集合B。对属于某一背景类的像元yk(i,j),若该像元中对应于该背景类的组分值不小于下限low(k),则将该像元加入到代表该类的端元束集Ak中,即:
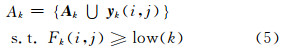
假设背景类的数目为c<p,那么,所有背景类别的端元束组成背景字典是Ab={A1,A2,…,Ac}。此时,low(k)的数值不宜小于0.5。进一步说明,在阈值low(k)约束下,所占面积较小的类别,其字典元素数会偏小,而部分面积较大的类别,其字典元素数会偏大,因此增加了额外的两个控制项,即子字典最小原子数和最大原子数。
1.3 基于重建误差的异常检测根据异常目标所表现出的低概率特性,背景字典不会包含其相关信息,因此,倘若以背景字典Ab重建原高光谱图像,那么包含异常目标的像元将出现大的重建误差。设仅在背景元素已知的情况下由DALM稀疏求解的系数估计是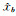 =
=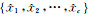 ,并设:
,并设:
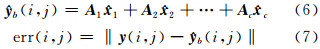
联系§1.2的wu(i,j),定义加权误差:

那么存在δ,使得如下假设成立:
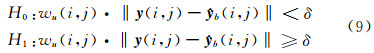
式中,H0表示非异常;H1表示异常。即若仅以背景字典表达,那些被认为是异常目标的像元将出现较大误差。
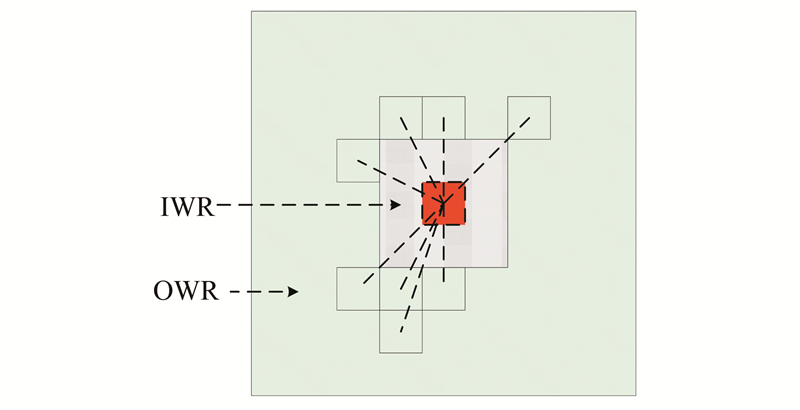
1.4 重建误差局部后处理异常像元不仅在由背景字典重建的误差图像中表现出离群性质,同时,其在局部空间必然与邻近像元呈现出非连续性特点,对此进行局部近邻分析处理。假设待检测像元为y(i,j),以该像元为中心定义双窗口[15](图 1),即内窗口(inner window region,IWR)与外窗口(outer window region,OWR),双窗口将像元的邻域自然地分为潜在目标区域的IWR,和潜在背景区域的OWR,IWR的尺寸不小于潜在目标的尺寸。局部后处理方法的思想为:在OWR内寻找与y(i,j)最邻近的K个像元 ,不失一般性,设
,不失一般性,设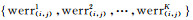 为这k个邻近像元的重建误差特征,werr(i,j)o为中心像元的重建误差特征,定义:
为这k个邻近像元的重建误差特征,werr(i,j)o为中心像元的重建误差特征,定义:
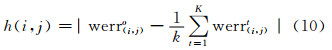
|
| 图 1 双窗口局部邻近像元关系 Fig. 1 Nearest Neighbor Analysis in Dual Window |
如果该值越小,表明中心像元与邻近像元越相似;相反,该值越大表明中心值越可能是异常,那么存在δ′,使得:
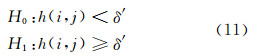
式中,H0表示不存在异常;H1表示存在异常。h(i,j)将字典构造的全局性与地物的局部连续性结合,有利于提高目标检测的精度。
2 异常检测实验本文采用模拟的异常目标与实际的感兴趣目标两种数据进行实验。首先采用盲分解方法建立背景字典,然后采用DALM进行稀疏求解,然后求得加权误差,最后进行局部邻近后处理。为便于描述,将式(7)、式(8)和式(10)对应的求解简称为DALM、加权DALM(weighted DALM,WDALM)和局部邻近分析WDALM(nearest neighbor analysis WDALM,NWDALM),并与经典的RX异常检测算法——全局RX(GRX)、局部RX(LRX)[16]及基于子空间模型扩展RX(subspace extension RX,SSRX[17])和基于聚类分析扩展RX(cluster extension RX,CluRX[4])的结果进行对比。其中,LRX算法计算也是采用双窗口分析的,为避免矩阵求逆的奇异问题,在它的协方差求逆计算过程中增加了正则项。所有算法计算得到的异常特征运用接收者操作特性(receiver operating characteristic,ROC)曲线评价性能,并用ROC曲线下面积(area under ROC curve,AUC)进行对比,较大的AUC代表了较好的性能。
2.1 模拟异常目标检测实验 2.1.1 数据描述取由AVIRIS传感器获得的位于美国内华达州LCVF区域一幅224个波段(去掉含水波段和噪声波段后为187个波段)、尺寸为160×120高光谱图植入1×1个像元。每一列都采用异常光谱与植入像元的光谱混合的方式植入异常信息,具体比例见表 1。表 1中两组比例混合,分别为1和2,第2组中异常光谱信号所占比例小,获取其异常估计更困难,这种设置有利于检验算法对亚像元异常目标的检测能力。植入异常后得到的影像见图 2(a)。为了检验算法在噪声环境下的稳定性,在植入异常后的影像加入高斯噪声,其信噪比SNR分别15 dB、25 dB和35 dB。
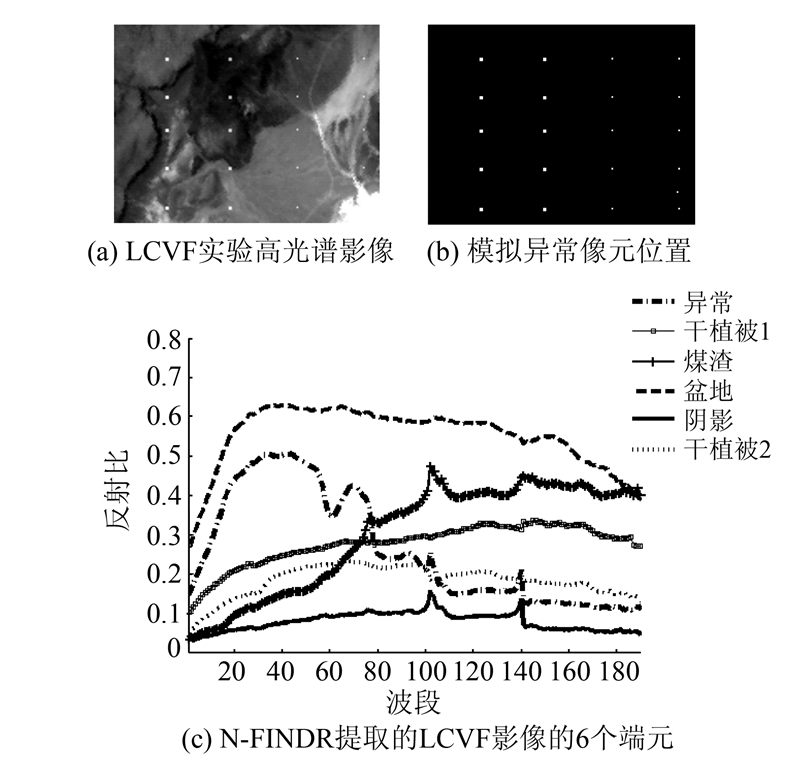
|
| 图 2 LCVF影像与模拟异常像元位置 Fig. 2 LCVF Image and the Position of Simulated Anomaly Target |
| 植入列 | 植入尺寸 | 测试组 | 异常信号混 合比重 | 背景像元信 号混合比重 |
| 第1列 |  | 1 2 | 0.8 0.6 | 0.2 0.4 |
| 第2列 |  | 1 2 | 0.6 0.4 | 0.4 0.6 |
| 第3列 |  | 1 2 | 0.4 0.2 | 0.6 0.8 |
| 第4列 |  | 1 2 | 0.4 0.2 | 0.6 0.8 |
对该图像采用N-FINDR提取了6个端元(见图 2)。定义a%=1%,low(k)=0.65,k=1,2,…,6,并设置子字典最小原子数为15,最大原子数为95,应用§1.2描述的算法进行分类后得到估计的背景字典Ab,其中包含了5类背景类,得到的字典大小分别为95、95、21、42、95,运用DALM计算得到对应的系数,从而根据上文描述的方法,对添加高斯噪声的影像进行了处理,分别得到了式(7)和式(8)对应的特征err和werr;双窗口的IWR依据表 1的目标尺寸定义为3×3,OWR定义为13×13(LRX算法的双窗口与此同),依据式(10)计算对应的特征h,并根据式(9)和式(11)参考图 2(b)进行ROC评价。
图 3(a)和图 3(b)为不同算法性能的对比,从结果来看,NWDALM算法在不同噪声条件下表现最稳健且AUC值最高,它同时考虑了全局和局部信息,结果优于运用全局信息的GRX、SSRX和CluRX结果和运用局部信息的LRX,稀疏重建DALM误差结果优于GRX算法。
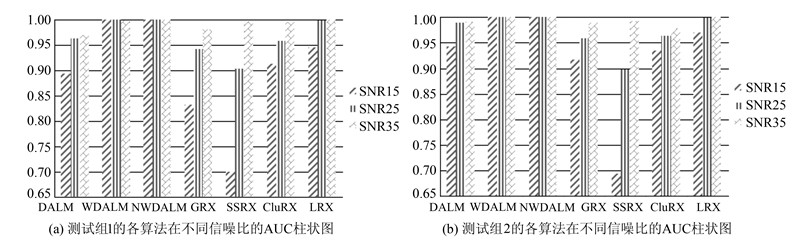
|
| 图 3 不同算法在不同信噪比条件下的AUC对比 Fig. 3 AUC Value for Different Algorithms Performance Under 3 Noisy Condition for LCVF AVIRIS Image |
利用光谱范围为650~1 100 nm、光谱分辨率为10 nm的液晶可调高光谱仪Nuance 获取如图 4(a)所示的以草地为背景的实验区域高光谱图像,光谱分辨率为10 nm,图中有两并行排列的对象是感兴趣目标。图 4(b)是波长位置为1 040 nm的高光谱图像,图像大小为100×100。对图像运用N-FINDR算法提取了5个端元,定义a%=1%,low(k)=0.65,k=1,2,…,5,同时为避免某一类的子字典规模过大,令子字典规模不得大于波段数,得到估计的背景字典Ab由4个背景类子字典构成,运用DALM计算得到对应的系数,从而根据上文描述的方法分别得到了特征err和werr;双窗口的IWR尺寸定义为7×7,OWR定义为13×13(LRX算法的双窗口与此同),计算对应的特征h。

|
| 图 4 Nuance高光谱成像草地背景下的异常目标检测 Fig. 4 Anomaly Detection in a Nuance Lawn Hyperspectral Image |
图 4(c)是验证结果的参考图像,白色为测试目标的样本区域。图 4(d)~4(e)分别是稀疏重建误差分析得到的两个异常特征WDALM和NWDALM的线性拉伸,图 4(f~i)是经典RX算法及其扩展得到异常特征的线性拉伸。根据图 4(c)计算不同算法的AUC值得到表 2,表 2为不同方法检测精度AUC值。从特征图和AUC值来看,稀疏重建误差及其扩展方法的结果优于全局RX算法及其扩展,即使本数据中的异常目标局部性质表现明显,但NWDALM和WDALM仍优于LRX,且在字典给定的条件下,它们的计算效率高于LRX。
| 方法 AUC值 | DALM | WDALM | NWDALM | GRX | SSRX | CluRX | LRX |
| 0.99 946 | 0.99 987 | 0.99 982 | 0.99 538 | 0.96 098 | 0.93 003 | 0.99 951 |
图 5(a)为由AVIRIS传感器获取的一机场局部的高光谱波长位置为2 161 nm的影像,以影像中的飞机为异常目标。图像尺寸为116×120,图像的光谱范围是369.85~2 506.81 nm,去掉因水吸收和低信噪比的波段后剩余189个波段。对图像定义端元数为8,a%=1.5%,low(k)=0.75,k=1,2,…,8,得到估计的背景字典Ab由5个背景类子字典构成。同以上实验,计算得到特征err和werr;双窗口的IWR尺寸定义为15×15,OWR定义为23×23(LRX算法的双窗口与此同),计算对应的特征h。

|
| 图 5 AVIRIS影像异常目标检测 Fig. 5 Anomaly Detection in an Airport AVIRIS Hyperspectral Image |
图 5(c)、5(d)分别是稀疏重建误差分析得到的两个异常特征WDALM和NWDALM的线性拉伸,图 5(e)、5(h)是经典RX算法及其扩展得到异常特征的线性拉伸。根据图 5(b)进行ROC评价不同算法,表 3为对应的AUC值。从AUC数值上看,WDALM的大于所有全局RX算法的值,NWDALM的结果好于WDALM和LRX算法;从结果图像来看,全局RX算法GRX和SSRX中感兴趣的目标特征与其他对象灰度对比不明显,尽管LRX取得较好结果,但相对于NWDALM的结果图,它对背景仍压制不足,而NWDALM结果中目标明显且光滑。
| 方法 AUC值 | DALM | WDALM | NWDALM | GRX | SSRX | CluRX | LRX |
| 0.946 9 | 0.994 3 | 0.996 1 | 0.958 4 | 0.949 8 | 0.950 5 | 0.995 8 |
本文利用异常目标的低概率特征和盲分解分析求得表达背景信息的冗余字典,以此为基础对每个像元进行稀疏回归,而回归误差表达了异常特征,并通过局部邻近分析增强结果。通过实验论证得到如下结论:(1)盲分解分析采用非监督的方式构建冗余字典描述背景是有效的;(2)背景字典重构和双窗口邻近分析综合了全局与局部两层异常判决信息,这大大增强了异常检测的可靠性;(3) NWDALM在不同的信噪比条件下的稳健表现表明本文方法是有效的。需要说明的是,仍有几点需要进一步加强,其一如果能通过流形嵌入的平滑约束对目标函数进行优化,将有益于利用图像空间和特征空间目标的连续特征;其二在地物类别覆盖面积差异较大的情况下,非监督构造的背景字典间易产生样本不平衡问题,这需要进一步的研究。
| [1] | Stein D W J, Beaven S G, Hoff L E, et al. Anomaly Detection from Hyperspectral Imagery[J]. IEEE Signal Processing Magazine, 2002, 19(1): 58-69 |
| [2] | Reed I S, Yu X. Adaptive Multiple-Band CFAR Detection of an Optical Pattern with Unknown Spectral Distrihution[J]. IEEE Trans Acou, Speech Signal Process, 1990, 38(10):1 760-1 770 |
| [3] | Kwon H, Nasrabadi N M. Kernel RX-algorithm: A Nonlinear Anomaly Detector for Hyperspectral Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 43(2),:388-397 |
| [4] | Duran O, Petrou M. A Time-Efficient Method for Anomaly Detection in Hyperspectral Images[J]. IEEE Transactions on Geoscience and Remote Sensing,2007,45(12): 3 894-3 904 |
| [5] | Bruckstein A M, Donoho D L, Elad M. From Sparse Solutions of Systems of Equations to Sparse Modeling of Signals and Images[J]. SIAM Review, 2009, 51(1): 34-81 |
| [6] | Wright J, Yang A Y, Ganesh A, et al. Robust Face Recognition via Sparse Representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227 |
| [7] | Chen Y, Nasrabadi N M, Tran T D. Hyperspectral Image Classification Using Dictionary-Based Sparse Representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10 PART 2): 3 973-3 985 |
| [8] | Chen Y, Nasrabadi N M, Tran T D. Sparse Representation for Target Detection in Hyperspectral Imagery[J]. IEEE Journal of Selected Topics in Signal Processing, 2011,5(3): 629-640 |
| [9] | Iordache M, Bioucas-Dias J M, Plaza A. Sparse Unmixing of Hyperspectral Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6 PART 1): 2 014-2 039 |
| [10] | Allen Y, Zhou Z, Ganesh A, et al. Fast l1-Minimization Algorithms for Robust Face Recognition[J]. IEEE Transactions on Image Processing, 2013,22(8): 3 234-3 246 |
| [11] | Chang C, Wu C, Tsai C. Random N-finder (N-FINDR) Endmember Extraction Algorithms for Hyperspectral Imagery[J]. IEEE Transactions on Image Processing, 2011, 20(3): 641-656 |
| [12] | Tang Xiaoyan,Gao Kun, Ni Guoqiang, et al. An Improved N-FINDR Endmember Extraction Algorithm Based on Manifold Learning and Spatial Information[J]. Spectroscopy and Spectral Analysis, 2013, 33(9): 2 519-2 524(唐晓燕,高昆,倪国强,等. 基于流形学习和空间信息的改进N-FINDR端元提取算法[J]. 光谱学与光谱分析,2013, 33(9): 2 519-2 524) |
| [13] | Luo B, Chanussot J, Doute S, et al. Empirical Automatic Estimation of the Number of Endmembers in Hyperspectral Images[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(1): 24-28 |
| [14] | Heinz D C, Chang C I. Fully Constrained Least Squares Linear Spectral Mixture Analysis Method for Material Quantification in Hyperspectral Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(3): 529-545 |
| [15] | Wang Ting, Du Bo, Zhang Liangpei.A Local Information-Base Kernel OSP Method for Target Detection[J]. Geomatics and Information Science of Wuhan University, 2013, 38(2):200-203(王挺,杜博,张良培. 顾及局域信息的核化正交子空间投影目标探测方法[J]. 武汉大学学报·信息科学版, 2013, 38(2):200-203) |
| [16] | Molero J M, Garzon E M, Garcia I, et al. Analysis and Optimizations of Global and Local Versions of the RX Algorithm for Anomaly Detection in Hyperspectral Data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013,6(2):801-814 |
| [17] | Ranney K I, Soumekh M. Hyperspectral Anomaly Detection Within the Signal Subspace[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(3): 312-316 |
 2015, Vol. 40
2015, Vol. 40


