2015, Vol. 40文章信息
- 余接情, 吴立新
- YU Jieqing, WU Lixin
- 球体坐标与SDOG-ESSG格网码的相互转换算法
- Transformation Algorithms Between Spheroid Coordinates System and SDOG-ESSG Grid Code
- 武汉大学学报·信息科学版, 2015, 40(8): 1116-1122
- Geomatics and Information Science of Wuhan University, 2015, 40(8): 1116-1122
- http://dx.doi.org/10.13203/j.whugis20140032
-
文章历史
- 收稿日期: 2014-01-09
2. 中国矿业大学物联网(感知矿山)研究中心, 江苏 徐州, 221008
2. IoT/Perception Mine Research Centre, China University of Mining and Technology, Xuzhou 221116, China
目前，球体空间格网已经成为地学研究中的重要工具和手段。地幔对流，地壳运动，地震海啸，大气对流(环流)等大尺度的三维地球系统问题常需借助球体空间格网对数据进行解译、分析、模拟及可视化[1, 2]。球体空间格网的研究主要集中在地球系统科学领域[3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]，也有少量出现在空间信息领域[14, 15, 16, 17]。前者重点在数值模拟，后者重点在数据组织，两者尚存在较大的鸿沟，需寻找一种较为通用的格网以连通两个领域的数据流，提高效率[18]。基于球体退化八叉树(spheroid degenerated octree grid,SDOG)的地球系统空间格网 (SDOG-based Earth System Spatial Grid,SDOG-ESSG)[1, 17, 19]可满足地球系统科学与空间信息领域的大部分要求，其本身亦是对地观测联盟(Group on Earth,GEO) 2012~2015年工作计划(www.earthobservations. org/docshow.php? id=129)中的一部分，有望作为地球系统科学领域与空间信息领域的连接桥梁，并成为一种重要的工具。
然而，格网只是一种空间框架，要在连接桥梁、数值模拟、数据组织、空间分析及量算等方面充分发挥作用，还需建立格网与现有空间参考的联系[20]。文献[20]给出了SDOG-ESSG与现有空间参考间相互转换的模式，如图 1所示。从图 1可以看出，球体坐标系与SDOG-ESSG格网码(简称SDOG-ESSG码)的相互转换方法是问题关键所在。为此，本文将围绕这一关键问题展开，提出两者相互间高效的转换算法，并在理论及实验层面上分别予以剖析与验证。
|
| 图 1 SDOG-ESSG与其他空间参考的相互转换 Fig. 1 Transformation Between SDOG-ESSG and Other Spatial References |
SDOG-ESSG是在经定位与定向的球体退化八叉树格网(SDOG)[16](图 2(a))的基础上沿径向二分细分或沿球面方向退化四叉树细分(图 2(b)、2(c))后的球体空间格网。退化八叉树的剖分次数称为主剖次，用p表示；径向或球面再细分的剖分次数称为副剖次，用f来表示。符号SDOG-ESSG(p,f)表示SDOG-ESSG经p次退化八叉树剖分后再经f次径向或球面再细分。特别地，沿径向再细分的格网称为SDOG-R-ESSG(图 2(b))，而沿球面再细分的格网称为SDOG-S-ESSG(图 2(c))，两者统称为SDOG-ESSG。
|
| 图 2 基于SDOG的地球系统空间格网 Fig. 2 SDOG-ESSG |
由于退化剖分的存在，SDOG-ESSG在径向上及纬向上呈层域及纬域分布的特点[19]。相邻两层域的格网的经距和纬距呈两倍关系，各层域所占据的径向空间以1/2的等比递减，其所拥有的球面层数呈2的指数递减。特殊地，最后两个层域的径向空间及球面层数相同。相邻两纬域间的格网的经距呈两倍关系，各纬域所占据的半纬空间(半球中0°~90°的纬向空间)以1/2的等比递减，其所拥有的纬带及经带总数呈2的指数递减。特殊地，最后两个纬域的半纬空间及纬带总数相同。文献[19]给出了任意层域b及纬域l的格网粒度(经距Δθ、纬距Δφ及径距Δr)的计算方法。式(1)和式(2)分别为SDOG-R-ESSG及SDOG-S-ESSG格网粒度的计算方法：
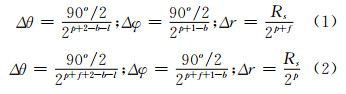
式中，Rs为SDOG-ESSG参考球体的半径;p和f分别为SDOG-ESSG的主剖次和副剖次。
2 相互转换的基本思路文献[21]通过对格网行列号的二进制位按序交错给出了Z曲线码(即Morton码)的生成算法。该算法具有较高的执行效率，时间复杂度为O(n)。在Morton码生成算法的基础上，文献[22]设计了SDOG退化Z曲线码的生成算法，即通过对格网的列-行-层序号按位交错来实现。
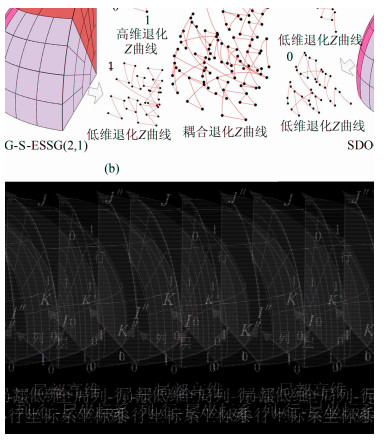
SDOG-ESSG采用耦合退化Z曲线对格网进行填充编码[17, 19]。耦合退化Z曲线是一种由多条退化Z曲线复合而成的填充曲线，其基本思想见图 3。SDOG-ESSG的剖分方法等价于先低维剖分(径向二分或退化四叉树剖分)，再对各部分分别进行高维剖分(退化八叉树剖分)；其中，低维剖分部分采用低维(1维或2维)退化Z曲线填充，而高维剖分部分采用高维(3维)退化Z曲线填充；按低维退化Z曲线的顺序依次连接各高维退化Z曲线所得到的完整曲线即为耦合退化Z曲线。耦合退化Z曲线的线性码是SDOG-ESSG码的主要组成部分。SDOG-ESSG码最终由BB、MC、OC、FSL、LD及HD 6部分依序组成。BB标识编码开始，始终为1；MC为格网类型码，0表示SDOG-R-ESSG，1表示SDOG-S-ESSG；OC为八分体码，计算方法见文献[22]；FSL为格网副剖次; LD及HD分别为低维退化Z曲线填充码及高维退化Z曲线填充码。因此，球体坐标与SDOG-ESSG码相互转换方法的关键在于主副剖次的计算及LD和HD的生成与反算。本文将球体坐标转为SDOG-ESSG码的过程称为正向转换，反之称为逆向转换。为了保证源数据精度的不损失，取最大粒度不大于源数据精度的格网为匹配格网。文献[19]给出了由点数据精度计算SDOG-ESSG格网粒度(即主剖次和副剖次)的方法。
|
| 图 3 SDOG-ESSG的耦合退化Z曲线填充 Fig. 3 The Curve Filling of SDOG-ESSG by Coupled Degenerated Z-curve |
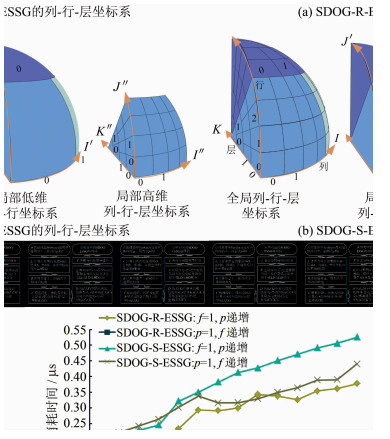
为实现LD和HD的生成与反算，需要为SDOG-ESSG建立一个层-列-行坐标系。沿经度、纬度及半径方向为所有格网建立的序号坐标系称为全局-列-行-层坐标系，分别用I、J、K来表示；为低维(或高维)剖分所得格网建立的序号坐标系称为局部低维(或高维)列-行-层坐标系，分别用I′(I″)、J′(J″)、K′(K″)来表示。 后者用于LD(或HD)的生成与反算，而前者用于球体坐标与后者的过渡。图 4显示了SDOG-ESSG的6种层-列-行坐标系。
|
| 图 4 SDOG-ESSG的6种层-列-行坐标系 Fig. 4 Six Column-row-layer Number Systems of SDOG-ESSG |
图 5显示了正向转换算法的基本流程。象限码计算方法见文献[22]。由层纬域的径向空间及半纬空间分布规律可推算出球体坐标计算层域及纬域的方法，结果见式(3)~(5)。其中，式(4)和式(5)分别为SDOG-R-ESSG及SDOG-S-ESSG的纬域计算公式。式(1)和式(2)给出了格网粒度的计算方法。在此基础上，可按式(6)计算格网的全局列-行-层坐标。由全局列-行-层坐标析出局部列-行-层坐标实质上是一个取整和求余的过程。式(7)给出了步骤D的计算方法。HD的生成可由K″、J″、I″依序进行二进制位交错而得。对于SDOG-R-ESSG，LD与K′相同；对于SDOG-S-ESSG，LD的生成需对J ′、I ′依序进行二进制位交错而得。在此基础上，步骤F将各部分码按各自位数依序进行组装，得到最终的SDOG-ESSG码。表 1列举了SDOG-ESSG码各部分占用的二进制位数[19]。
|
| 图 5 正向转换的算法过程 Fig. 5 The Procedure of Forward Transformation |
| BB | MC | OC | FSL | LD | HD | |
| SDOG-R-ESSG | 1 | 1 | 3 | 5 | f | 3 p |
| SDOG-S-ESSG | 1 | 1 | 3 | 5 | 2 f | 3 p |
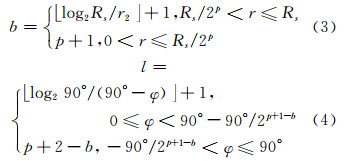
式中，
为向下取整运算；\为整除运算; % 为求余运算；对于SDOG-R-ESSG，S为∞，B为2f； 对于SDOG-S-ESSG，S为2f，B为∞；下同。
步骤 A~D涉及整除、求余、取整及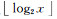 
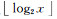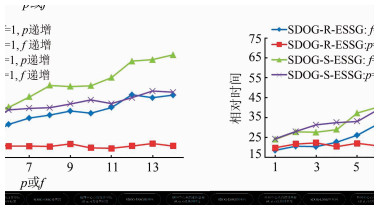
运算，最高复杂运算为 。由于式(3)~(5)中的 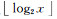的值域不会超过[0,p+f]，因而可采用文献[22]给出的方法进行加速，加速后的时间复杂度为O(n)，其中n<p+f。步骤E为p次局部高维列-行-层序的二进制位交错运算及f次局部低维层序或列-行序的二进制位交错运算，时间复杂度也为O(n)。因此，正向转换算法的时间复杂度为O(n)。 本文在PC环境下 (CPU：2.3 GHz双核，内存：2 GB，下同)，对该算法进行了实验测试。图 6给出了某一球体坐标点转为不同格网粒度的SDOG-ESSG码所消耗的时间。图 7显示了该算法与一次除法运算的时间之比。可以看出，正向转换算法的时间消耗基本随p或f增大而线性增大(或不变)，每秒大约能进行106~107次转换，1次转换相当于101~102次的除法运算。
|
| 图 6 正向转换的时间消耗 Fig. 6 Time Consuming of Forward Transformation |
|
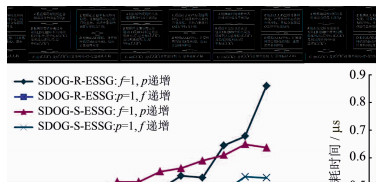
| 图 7 正向转换与1次除法运算的时间之比 Fig. 7 The Rate of Time Consuming Between Once Forward Transformation and Once Division Operation |
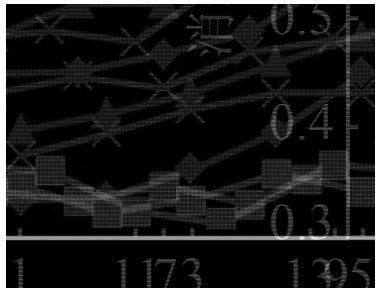
逆向转换是正向转换的逆过程，基本步骤如图 8所示。主剖次p可由HD二进制位数的1/3计算而得，其余重要信息(如FSL、LD、HD)均可从步骤A的编码析取过程中获取。在析取各部分码之前，需寻找第1位非零二进制位(即格网的标志位)的位置t。位置t的查找可采用二分法以提高效率，得出t后可按实际二进制位数(表 1)依次取出各部分码。在得到局部低维及高维列-行-层坐标后，可按式(8)方法计算全局列-行-层坐标。由各层纬域的球面层数及纬带数量关系可推出全局列-行-层序坐标计算层域及纬域的方法，见式(9)~(11)。其中，式(10)和式(11)分别为SDOG-R-ESSG及SDOG-S-ESSG的纬域计算公式。格网的粒度的计算方法可参见式(1)和式(2)。式(12)给出了归化坐标及反归化计算的方法。
|
| 图 8 逆向转换的算法过程 Fig. 8 Procedure of Backward Transformation |
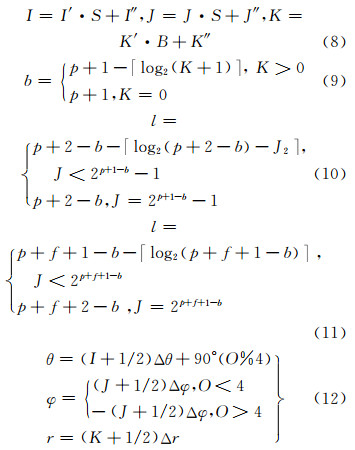
式中，
为向上取整运算。
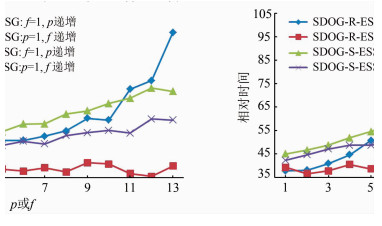
步骤A涉及二分查找运算，时间复杂度为O(log2n),其中，n为p和f的线性函数。步骤B涉及二进制分离操作，最高时间复杂度为O(n)；步骤D涉及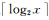 
运算，与上文类似，同样可优化为时间复杂度为O(n)的计算；步骤C和步骤E的最高复杂运算为求余运算，可忽略不计。因此，本转换算法的最高时间复杂度为O(n)。图 9显示了逆向转换的消耗时间；图 10显示了逆向转换与1次除法运算的时间之比。可以看出，与正向转换一致，逆向转换基本随p或f增大而线性增大(或不变)，每秒大约能进行106~107次转换，1次转换相当于101 ~ 102次的除法运算。
|
| 图 9 逆向转换的时间消耗 Fig. 9 Time Consuming of Backward Transformation |
|
| 图 10 逆向转换与1次除法运算的时间之比 Fig. 10 Rate of Time Consuming Between Once Backward Transformation and Once Division Operation |
SDOG-ESSG可满足地球系统科学与空间信息领域大部分要求，其本身也成为了对地观测联盟(Group On Earth,GEO) 2012~2015年度工作计划建设的一部分。 本文针对SDOG-ESSG与现有空间参考间相互转换的关键问题——球体坐标与SDOG-ESSG码的相互转换展开了研究。首先引进了6种列-层-序坐标，导出了层域、纬域及各列-层-序坐标的计算公式；在此基础上，利用Morton码的位交叉特性实现了球体坐标与SDOG-ESSG码的正向转换与逆向转换。之后，进一步对转换算法的时间效率进行了理论分析以及实验验证。最终结果表明，本文所提出的球体坐标与SDOG-ESSG码的正向和逆向转换算法非常高效；两转换算法的时间消耗基本与主剖次p和副剖次f呈线性关系，时间复杂度为O(n)； 在普通PC下，每秒能实现106~107次的转换运算，1次转换相当于101~102次的除法运算。
| [1] | Wu Lixin, Yu Jieqing. Earth System Spatial Grid and Its Application Modes [J]. Geography and Geo-Information Science, 2012, 28(1): 7-13 (吴立新,余接情,地球系统空间格网及其应用模式[J]. 地理与地理信息科学, 2012, 28(1): 7-13) |
| [2] | Cao Xuefeng. Research on Earth Sphere Shell Space Grid Theory and Algorithms[D]. Zhengzhou: Information Engineering University, 2012 (曹学峰. 地球圈层空间网格理论与算法研究[D]. 郑州:信息工程大学, 2012) |
| [3] | Zhu Jieshou, Cao Jiamin, Cai Xuelin, et al. Study for Three-dimensional Structure of Earth Interior and Geodynamics in China and Adjacent Land and Sea Regions[J]. Advance in Earth Science, 2003,18(4):497-503 (朱介寿,曹家敏,蔡学林,等.中国及邻近陆域海域地球内部三维结构及动力学研究[J]. 地球科学进展, 2003,18(4): 497-503) |
| [4] | Mooney W, Laske G, Masters G. CRUST 5.1: A Global Crustal Model at 5×5 Degrees[J]. Journal of Geophysical Research,1998, 103(B1): 727-747 |
| [5] | Zhao D. Global Tomographic Images of Mantle Plumes and Subducting Slabs: Insight into Deep Earth Dynamics[J]. Physics of The Earth and Planetary Interiors, 2004,146(1-2): 3-34 |
| [6] | Kageyama A. Dissection of a Sphere and Yin-Yang Grids[J]. Journal of the Earth Simulator, 2005,3: 20-28 |
| [7] | Baumgardner J R. Three-dimensional Treatment of Convective Flow in the Earth's Mantle[J]. Journal of Statistical Physics, 1985,39(5): 501-511 |
| [8] | Ballard S, Hipp J R, Young C J. Efficient and Accurate Calculation of Ray Theory Seismic Travel Time Through Variable Resolution 3D Earth Models[J].Seismological Research Letters, 2009,80(6): 989-999 |
| [9] | Harder H, Hansen U. A Finite-volume Solution Method for Thermal Convection and Dynamo Problems in Spherical Shells[J]. Geophysical Journal International, 2005,161(2): 522-532 |
| [10] | Stemmer K, Harder H, Hansen U. A New Method to Simulate Convection with Strongly Temperature and Pressure-dependent Viscosity in a Spherical Shell: Applications to the Earth's Mantle[J]. Physics of the Earth and Planetary Interiors, 2006,157(3-4): 223-249 |
| [11] | Tsuboi S, Komatitsch D, Chen J, et al. Computations of Global Seismic Wave Propagation in Three Dimensional Earth Model[M]. Berlin: Springer Berlin/Heidelberg, 2008 |
| [12] | Stadler G, Gurnis M, Burstedde C, et al.The Dynamics of Plate Tectonics and Mantle Flow: from Local to Global Scales[J]. Science, 2010,329(5 995):1 033-1 038 |
| [13] | Komatitsch D, Ritsema J, Tromp J. The Spectral-element Method, Beowulf Computing, and Global Seismology[J]. Science, 2002,298(5 599): 1 737-1 742 |
| [14] | Wang Jinxin, Lu Fengnian, Guo Tongde. Global 3D-Grids Based on Great Circle Arc QTM[J]. Geomatics and Information Science of Wuhan University, 2013,38(6):344-348 (王金鑫, 禄丰年, 郭同德. 球体大圆弧QTM八叉树剖分[J]. 武汉大学学报·信息科学版, 2013,38(6): 344-348) |
| [15] | Han Yu. Construction and Demonstration of Extend-diamond Ball Grid[D]. Nanjing: Nanjing Normal Univerisy, 2012 (韩宇. 扩展菱形球体网格构建与示范研究[D]. 南京:南京师范大学, 2012) |
| [16] | Wu Lixin, Yu Jieqing. Global 3D-Grid Based on Sphere Degenerated Octree and Its Distortion Features[J]. Geography and Geo-Information Science, 2009, 25(1): 1-4(吴立新, 余接情. 基于球体退化八叉树的全球三维网格与变形特征[J]. 地理与地理信息科学, 2009, 25(1): 1-4) |
| [17] | Yu Jieqing, Wu Lixin.Adaptable Spheroid Degenerated-Octree Grid and Its Coding Method[J]. Geography and Geo-Information Science, 2012, 28(1):14-18 (余接情,吴立新. 适应性球体退化八叉树格网及其编码[J]. 地理与地理信息科学, 2012,28(1): 14-18) |
| [18] | Yu J, Wu L, Guo Z, et al. SDOG-based Multi-scale 3D Modeling and Visualization on Global Lithosphere[J]. Sci China Earth Sci, 2012, 55(6): 1 012-1 020 |
| [19] | Yu Jieqing. Earth System Spatial Grid and Its Applications on Three-dimensional Modeling[D]. Beijing: Beijing Normal University, 2012 (余接情. 地球系统空间格网及其三维建模应用[D]. 北京:北京师范大学, 2012) |
| [20] | Yu J, Wu L, Jia J.ESSG-Based Global Spatial Reference Frame for Datasets Interrelation[C].ISPRS WebMGS 2013 & DMGIS 2013, Xuzhou, China, 2013 |
| [21] | Orenste J A. A Class of Data Structures for Associative Searching[C].The Fourth ACM SIGACT-SIGMOD Symposium on Principles of Database Systems, Portland, Oregon, 1985 |
| [22] | Yu Jieqing, Wu Lixin. On Coding and Decoding for Sphere Degenerated 2Octree Grid [J]. Geography and Geo-Information Science, 2009, 25(1):5-9 (余接情, 吴立新. 球体退化八又树网格编码与解码研究[J].地理与地理信息科学, 2009, 25(1): 5-9) |