文章信息
- 王磊, 赵学胜, 赵龙飞, 殷楠
- WANG Lei, ZHAO Xuesheng, ZHAO Longfei, YIN Nan
- 基于多层次QTM的球面Voronoi图生成算法
- Multi-level QTM Based Algorithm for Generating Spherical Voronoi Diagram
- 武汉大学学报·信息科学版, 2015, 40(8): 1111-1115
- Geomatics and Information Science of Wuhan University, 2015, 40(8): 1111-1115
- http://dx.doi.org/10.13203/j.whugis20140381
-
文章历史
- 收稿日期: 2014-05-13
Voronoi图(以下简称V图)作为一种重要的数据模型,已广泛应用于地图点群综合[1]、空间关系计算[2]、地图矢量化[3]等领域。近年来,随着数字地球的发展,球面Voronoi图也成为GIS领域的研究热点,并被应用于全球空间索引、球面插值、球面动态操作等领域[4]。与此同时,众多学者提出了球面V图的生成算法,按使用数据模型的不同,主要分为基于矢量的算法和基于栅格的算法。
大多数矢量算法[5, 6, 7, 8, 9]仅考虑球面点集V图的生成。Christopher等[10]将"点-线"模型[11]扩展到球面上,将复杂实体分解为点、线等简单实体来生成V图。这种方法虽然能够生成线、面等复杂实体的V图,但所用的数据结构和计算过程十分复杂,不利于全球海量数据的多层次表达[4]。童晓冲等[12]将球面偏置曲线用到球面V图生成中,该方法虽然能够生成球面不同集合之间的矢量V图,但在大数据量的处理方面有一定的局限性,同样不利于全球海量数据的处理[12]。
为了克服矢量算法的缺陷,一些学者提出了基于栅格(全球离散格网)的球面V图生成算法,如QTM (quaternary triangular mesh)算法[4, 13]和基于六边形格网的算法[14, 15]等,主要利用球面三角形和六边形扩张生成点集、线集和面集的V图。然而,随着格网层次的增大,格网数据量与V图生成时间都呈指数增长,致使在高层次时效率较低;且达到一定层次后,格网数据量过大,计算机内存溢出,算法无法执行。
针对上述问题,本文利用球面四元三角格网的层次性,提出了一种基于多层次QTM的球面V图生成算法。为减少算法中不必要的计算和数据存储,首先用全球低层次的单一分辨率QTM格网生成球面V图,然后对V图边界格网进行再次剖分,以得到下一层次的V图,重复进行,直至达到目标层次。最后,设计了相应的实验验证本文算法的正确性和可行性。
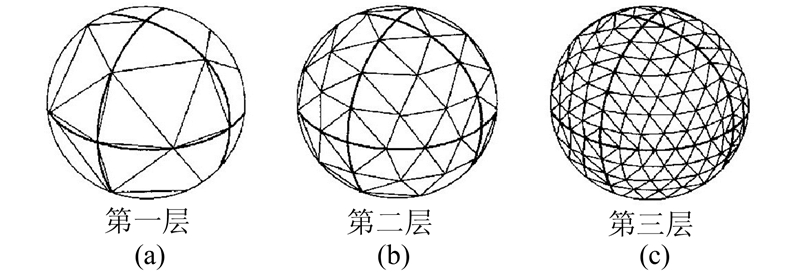
1 QTM层次结构QTM首先由Dutton提出[16],其层次剖分示意图如图 1所示。QTM具有良好的层次性和嵌套性,保证了格网形状和面积近似相等,具有典型的栅格模型特征[17]。因此,本文选取QTM作为球面V图生成的基础格网,并采用Goodchild提出的等三角形投影编码[18]作为QTM的编码方案。
|
| 图 1 QTM的层次剖分 Fig. 1 Hierarchical Subdivision of QTM |
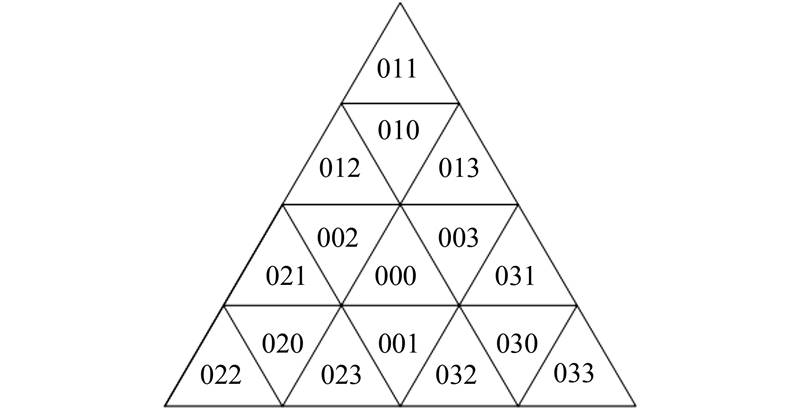
等三角形投影编码具有方向性:中间的三角形为"0",上或下三角形为"1 ",左三角形为" 2",右三角形为"3"。0号八分体第二层的编码方案如图 2所示。其中编码的第一位为八分体号。基于该方案的编码与经纬度转换方法及邻近搜索方案参见文献[13, 19]。
|
| 图 2 等三角形投影编码 Fig. 2 Equal-triangles Projection Encoding Method |
QTM的层次性是本文利用多层次QTM生成球面V图的基础。QTM下一层次的格网可通过对上一层格网直接剖分得到,相应的格网编码也可由上一层次的编码在末尾加上一位得到,如图 3所示。

|
| 图 3 QTM的层次性 Fig. 3 The Hierarchy of QTM |
给定一个区域Ω、一系列的实体si(i=1,2,3,…,n)和一个距离函数d,则实体si的Voronoi区域Vi可以通过式(1)定义:
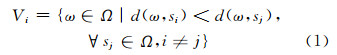
对于一个平面区域,距离d可以为欧氏距离,但对于球面,距离d应定义为大弧距离,如式(2):
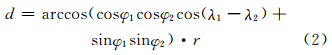
式中,(λ1,φ1)和(λ2,φ2)为球面上两点的经纬度;r为球的半径。 如果将式(1)中的距离函数d定义为式(2)所示的大弧距离,ω定义为QTM格网单元,Ω定义为整个球面,则式(1)所表述的即为基于QTM格网的球面V图。
2.2 球面Voronoi图生成算法与边界提取算法根据定义,生成球面V图与边界提取算法最关键步骤是为球面上每一个QTM格网确定所属的Voronoi区域。因此,可采用确定归属算法,依次计算每个格网到所有种子点的距离,并通过比较得到距离最短的种子点作为该格网的归属[20];也可以采用扩张算法,通过种子点(或线、面)的扩张得到该种子点(或线、面)的"势力范围",扩张算法详见文献[4, 13, 14, 15]。
利用上述算法,可以得到球面上每个格网所属的Voronoi区域。为获取各Voronoi区域的边界,本节提出了基于QTM的Voronoi边界提取算法,其基本原理为:
若一个格网自身和它的三个边邻近格网(左邻近、右邻近和顶邻近)属于两个或两个以上的Voronoi区域,则该格网位于Voronoi边界上;相反地,若格网自身和它的三邻近格网都属于同一个Voronoi区域,则该格网位于Voronoi区域的内部。
因此,依次计算每个格网的三个边邻近格网(具体算法参见文献[13]),并比较他们所属的Voronoi区域,即可判断该格网是否为边界格网。
3 多层次QTM的球面Voronoi图生成算法考虑到确定归属算法相对于扩张算法具有较好的精度[20],本文将在单一层次确定归属算法的基础上设计实现基于多层次QTM的球面V图生成算法。
图 4(a)、图 4(c)为分别利用第7层和第9层格网,以全球所有国家中心点作为种子点生成的球面V图;图 4(b)、图 4(d)分别为相应的局部放大视图。

|
| 图 4 利用不同层次的格网生成的球面V图 Fig. 4 Voronoi Diagrams of Different Levels |
从图 4中可以看出,利用不同层次的QTM生成的球面V图,Voronoi区域内部基本一致,不同之处仅在于,利用低层次格网生成的球面V图边界较粗,而利用高层次格网生成的球面V图边界较为精细。因此,在生成高层次的球面V图时,为减少格网数据量和计算量,可在Voronoi区域内部使用低层次的格网,而在Voronoi区域边界附近使用高层次的格网。即先用低层次格网生成球面V图,然后对Voronoi区域边界进行再次剖分,进而得到高层次的球面V图,算法具体原理及步骤如下。
1)利用层次较低的单一层次QTM格网生成初始层次的球面V图,提取Voronoi边界格网并存储边界格网的顶点坐标、自身及邻近格网的归属信息。
2)对边界格网进行再次剖分,得到下一层次的格网,并存储子格网的顶点坐标、中心点坐标、自身及邻近格网的归属信息。
3)确定子格网的归属。
若某一△T为边界三角形,且△T自身及其邻近格网分别属于Voronoi区域A、B、C、D(对应的种子点分别为a、b、c、d),则△T的子格网T1、T2、T3、T4所属的Voronoi区域必定为Voronoi区域A、B、C、D中的一个。因此,在确定子格网T1、T2、T3、T4的归属时,只需要计算子格网中心点到种子点a、b、c、d的距离,并通过比较得到最近的即可。
4)利用边界提取算法对边界格网的子格网进行边界提取。
5)重复步骤2)~4),直至达到指定层次。
4 实验与分析实现本文算法所用的编程语言为C++,球面V图显示所用的三维图形接口为Microsoft DirectX SDK (August 2009);硬件环境为Intel (R) Core (TM)2Quad,CPU Q8400@2.66 GHz,2.00 GB内存。在上述环境中,对本文算法进行了实现,并与单一层次的确定归属算法和扩张算法进行了对比。
4.1 实验结果为测试本文算法V图生成时间与QTM层次的关系,本文以第5层为初始层次,用100个种子点生成相应目标层次的V图,所用时间如图 5所示。图 5中的初始层次时间指计算初始层次V图所用的时间。从图 5中可以看出,该部分时间为恒定值且相对较少;过渡层次时间指由初始层次计算得到目标层次V图所用的时间,该部分时间与目标层次呈近似指数关系,算法的总时间也主要由这部分时间决定。

|
| 图 5 Voronoi图生成时间与目标层次的关系 Fig. 5 Relationship Between Generating Time and Level |
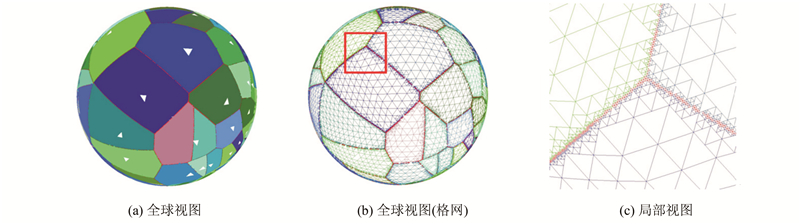
图 6为利用本文算法,以第5层为初始层次生成的第9层球面点集V图。从图 6中可以看出,本文算法生成的球面V图仅在Voronoi区域边界处使用了高分辨率的格网,而在Voronoi区域内部使用低分辨率的格网,从而减少不必要的计算和数据存储,以提高算法的效率。
|
| 图 6 基于多层次QTM的球面V图 Fig. 6 Voronoi Diagram Based on Multi-level QTM |
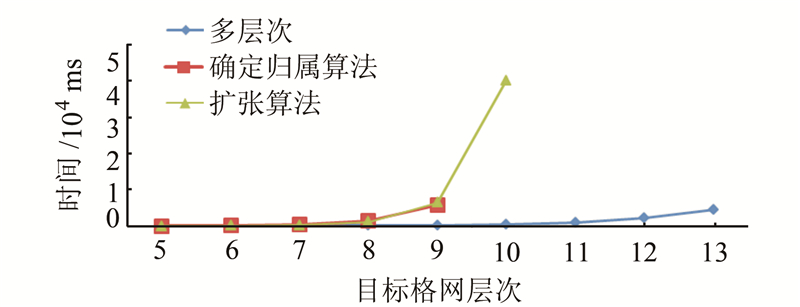
为进行效率对比,分别对本文算法、基于单一层次QTM的确定归属算法和扩张算法进行了测试,利用相同的种子点数,以第5层为初始层次生成各目标层次的球面V图,所用时间如表 1和图 7所示。
| 层次 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 扩张算法 | 12.5 | 45.6 | 201.4 | 1 152.9 | 6 434.8 | 40 094.0 | - | - | - |
| 确定归属算法 | 22.4 | 114.5 | 3 99.4 | 1 439.8 | 5 808.8 | - | - | - | - |
| 多层次算法 | 22.4 | 40.5 | 78.8 | 136.0 | 257.7 | 499.9 | 1 033.9 | 2 145.8 | 4 512.6 |
| 注:表中"-"表示达到相应层次时,由于计算机内存超限,算法在当前实验环境下无法执行。 | |||||||||
|
| 图 7 不同算法生成球面Voronoi图所用时间 Fig. 7 Generating Time of Different Algorithms |
从图 7中可以看出,虽然三种算法球面V图的生成时间都与目标格网层次呈近似指数关系,但相较单一层次的确定归属算法和扩张算法,本文算法大大降低了球面V图的生成时间。这是由于在多层次处理过程中,只有生成初始层次的V图时需要处理所有QTM格网,过渡层次只处理位于边界上的QTM格网,并且只需要计算并比较子格网到父格网及父格网的邻近格网的归属种子点的距离,而不需要计算到所有种子点的距离,这在很大程度上减小了计算量,从而减少了生成V图所用的时间。
此外,单一层次的确定归属算法和扩张算法,当格网层次增大时,格网数据量增大较快,在本文实验环境下分别能最多处理至第9层和第10层;而多层次算法由于需要处理的数据量相对较少,可以生成更高层次的球面V图,本文实验计算至第13层。
5 结语本文在分析基于单一层次QTM的球面V图生成算法的基础上,提出了一种基于多层次QTM的球面V图生成算法,并将该算法与单一层次的确定归属算法和扩张算法进行了对比,得出结论如下。
1)相对于单一层次的确定归属算法和扩张算法,本文算法的效率分别提高了22倍和25倍(第9层);
2)相对于单一层次的确定归属算法和扩张算法,本文算法能够生成更高层次的球面V图。
由于本文使用的是QTM格网的三(边)邻近搜索,在边界提取过程中会出现边界三角形提取不完全的情况,致使边界出现"间断"现象,在下一步研究中,应着手解决这一问题。
| [1] | Yan Haowen, Wang Bangsong. A MWVD-based Algorithm for Point Cluster Generation[J]. Geomatics and Information Science of Wuhan University, 2013, 38(9): 1 088-1 091(闫浩文, 王邦松. 地图点群综合的加权Voronoi算法[J]. 武汉大学学报·信息科学版, 2013, 38(9): 1 088-1 091) |
| [2] | Wang Zhonghui, Yan Haowen. Computation of Direction Relations Between Object Groups Based on Direction Voronoi Diagram Model[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 584-588(王中辉,闫浩文. 基于方向Voronoi图模型的群组目空间方向关系计算[J]. 武汉大学学报·信息科学版, 2013, 38(5): 584-588) |
| [3] | Hu Wei, Tao Weidong, Yuan Zhenyu, et al. A Method of Vectorization of Scanning Map Based on Voronoi Diagrams[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4): 470-474(胡玮, 陶伟东, 苑振宇, 等. 一种Voronoi图的扫描地图矢量化方法[J]. 武汉大学学报·信息科学版, 2013, 38(4): 470-474) |
| [4] | Chen J, Zhao X,Li Z. An Algorithm for the Generation of Voronoi Diagrams on the Sphere Based on QTM[J]. Photogrammetric Engineering & Remote Sensing, 2003, 69 (1):79-89 |
| [5] | Augenbaum J M, Peskin C S. On the Construction of the Voronoi Mesh on a Sphere[J]. Journal of Computational Physics, 1985, 59(2): 177-192 |
| [6] | Robert J, Renka R. Delaunay Triangulation and Voronoi Diagram on the Surface of a Sphere[J]. ACM Transactions on Mathematical Software, 1997, 23(3):416-434 |
| [7] | Ma Y, Chen Q. Fast Delaunay Triangulation and Voronoi Diagram Generation on the Sphere[C].The Second World Congress on Software Engineering, Wuhan, China, 2010 |
| [8] | Dinis J, Mamede M. Sweeping the Sphere[C]. 2010 International Symposium on Voronoi Diagrams in Science and Engineering, Quebec, Canada, 2010 |
| [9] | Hyeon-Suk N, Chung-Nim L, Otfried C. Voronoi Diagrams on the Sphere[J]. Computation Geometry: Theory and Applications, 2002, 23(2):183-194 |
| [10] | Christopher G, Mir A M. Towards the Global GIS[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2000, 55(3):150-163 |
| [11] | Yang W, Christopher G. Managing Spatial Objects with the VMO-Tree[C]. The 7th International Symposium on Spatial Data Handling, Netherlands, 1996 |
| [12] | Tong Xiaochong, Ben Jin, Zhang Yongsheng. The Generation Algorithm for Spherical Voronoi Diagram of Different Aggregation[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(1):83-89(童晓冲, 贲进, 张永生. 不同集合的球面矢量Voronoi图生成算法[J]. 测绘学报, 2006, 35(1): 83-89) |
| [13] | Zhao Xuesheng. Spherical Voronoi Data Model Based on QTM [M]. Beijing: Surveying and Mapping Press, 2004(赵学胜. 基于QTM的球面Voronoi数据模型[M]. 北京:测绘出版社, 2004) |
| [14] | Ben Jin, Tong Xiaochong, Zhang Heng, et al. A Spherical Voronoi Algorithm Based on Hexagonal Grid [J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2006, 23(5): 328-330(贲进, 童晓冲, 张衡, 等. 基于球面六边形格网的球面Voronoi图生成算法[J]. 测绘科学技术学报, 2006, 23(5): 328-330) |
| [15] | Tong Xiaochong, Ben Jin, Zhang Yongsheng. Expression of Spherical Entities and Generation of Voronoi Diagram Based on Truncated Icosahedron DGG [J]. Geomatics and Information Science of Wuhan University, 2006, 31(11):966-970(童晓冲, 贲进, 张永生. 基于二十面体剖分格网的球面实体表达与Voronoi图生成[J]. 武汉大学学报·信息科学版, 2006, 31(11): 966-970) |
| [16] | Dutton G. Modeling Locational Uncertainty via Hierarchical Tessellation[M]. London:Taylor & Francis, 1989 |
| [17] | Sun Wenbin, Zhao Xuesheng. A Hierarchical Seamless Model of Spatial Data Based on QTM [J]. Journal of China University of Mining & Technology, 2008, 37(5):675-679(孙文彬, 赵学胜. 基于QTM的空间数据无缝层次建模[J]. 中国矿业大学学报, 2008, 37(5):675-679) |
| [18] | Goodchild M F, Yang S, Dutton G.Spatial Data Representation and Basic Operations for a Triangular Hierarchical Data Structure [P]. US:National Center for Geographic Information and Analysis, 1991 |
| [19] | Sun Wenbin, Zhao Xuesheng. Algorithm of Neighbor Finding on Sphere Triangular Meshes with Quaternary Code [J]. Geomatics and Information Science of Wuhan University, 2007, 32(4): 350-352(孙文彬, 赵学胜. 球面Quaternary编码的球面三角格网邻近搜索算法[J]. 武汉大学学报·信息科学版, 2007, 32(4):350-352) |
| [20] | Wang Lei, Zhao Xuesheng, Cao Wenmin, et al. A GPU-Based Algorithm for the Generation of Spherical Voronoi Diagram in QTM Mode[C]. ISPRS WebMGS 2013 & DMGIS 2013,Xuzhou,China, 2013 |
 2015, Vol. 40
2015, Vol. 40


