文章信息
- 张珣, 钟耳顺, 张小虎, 王少华, 李绍俊
- ZHANG Xun, ZHONG Ershun, ZHANG Xiaohu, WANG Shaohua, LI Shaojun
- 一种尺度效应指数修正的格网数据示意地图制图算法
- A Modified Algorithm to Construct Gridded Area Cartograms by Scale Effect Index
- 武汉大学学报·信息科学版, 2015, 40(8): 1100-1104
- Geomatics and Information Science of Wuhan University, 2015, 40(8): 1100-1104
- http://dx.doi.org/10.13203/j.whugis20130370
-
文章历史
- 收稿日期: 2013-07-29
2. 中国科学院地理科学与资源研究所, 北京, 100101;
3. 南京农业大学国家信息农业工程技术中心江苏省信息农业高技术研究重点实验室, 江苏 南京, 210095
2. Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China;
3. National Engineering and Technology Center for Information Agriculture, Jiangsu Key Laboratory for Information Agriculture, Nanjing Agricultural University, Nanjing 210095, China
现代统计专题图的主要表达方式是从传统的纸质地图表达方式中延伸而来[1, 2, 3]的。为了解决经典统计专题地图表达与统计数据内涵不一致的问题,研究人员做了开拓性的研究,改变传统地图空间参考的数学法则,逐渐形成了一套新的针对研究对象属性特征的地图表现框架,即示意地图(cartogram)[4]。
规则格网化的统计数据可以有效弱化可塑面积单元对数据分析和表达的影响,使研究结果更易于理解[5]。因此,对行政区划单元的统计数据进行格网化处理是统计数据空间分析和表达的常用处理方法[6]。然而,已有的面域示意地图制图算法往往不适用于格网统计数据,主要表现为:1)小尺度的格网统计数据具有细节信息丰富、局部差异大的特点;2)已有的面域示意地图算法对数据的局部差异变化敏感,不适用局部差异较大的示意地图制图。针对该问题,本文提出了一种基于局部尺度效应指数修正的格网面域示意地图的表达算法,并将其应用在北京市人口统计数据上,以此完善地理信息系统中的格网统计地图表达手段。
1 面域示意地图与统计数据的地图表达 1.1 面域示意地图示意地图能够较好地表达人们对统计数据的认识,其基本目标是使地图呈现的多边形几何形状特征与实际反映的对象属性特征一致。其中常用的技术是使地图多边形面积与其属性一致,即面域示意地图(area cartogram),又称为面域拓扑地图[7]。现代地图制图研究人员基于GIS采用坐标转换等类投影的方法,实现了多种面域示意图的表达方法[8, 9, 10, 11, 12, 13, 14, 15, 16, 17]。这些地图表达方式被广泛地应用于全球尺度或国家尺度的人口、GDP等统计要素的可视化表达过程中,为研究人员、社会公众提供了认识世界的新视角[18, 19]。其中Gastner-Newman的diffusion based method算法由于保持了原始多边形的几何特征、连续性及其物理含义,并且与实际的地理空间过程相一致等特征,得到了广泛认可和应用[14]。
1.2 Gastner-Newman算法及其缺陷从数学表达来讲,面域示意地图的表达主要是寻求一个转换,将传统地图的坐标转换成另外一个坐标,从而满足面域示意地图的基本要求,即转换函数T: g →T( g ),其雅克比矩阵与属性密度ρ( g )成比例:

式中, 为平均属性密度。式(1)并不能唯一确定面域示意地图转换方式,需要额外的条件加以限制。Gastner和Newman设计提出了一种基于二维扩散模型的面域示意图表达方式,对原始密度不一致的多边形体系,采用扩散的方法,使得地图中处处密度一致。根据Fick第一定律,扩散通量为:
为平均属性密度。式(1)并不能唯一确定面域示意地图转换方式,需要额外的条件加以限制。Gastner和Newman设计提出了一种基于二维扩散模型的面域示意图表达方式,对原始密度不一致的多边形体系,采用扩散的方法,使得地图中处处密度一致。根据Fick第一定律,扩散通量为:

式中,v( g ,t)是速度扩散系数;ρ( g ,t)是密度。从扩散的物理学意义上来讲,扩散是沿着密度的梯度进行的,因此,有:

式(3)表明,扩散是从密度大的区域向密度小的区域进行,密度差别越大,扩散强度也就越大。同时,扩散过程的局部方程为:
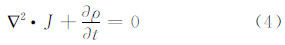
由式(2)~(4)可以得到扩散方程:

利用上述扩散方程制作示意地图的过程就是将原始的多边形属性密度 ρ作为求解偏微分方程(5)中的ρ( g ,t),而扩散速度v( g ,t)可以用属性密度ρ表示为式(6),则 g (t)可表示为式(7):
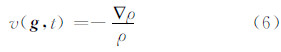
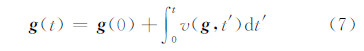
在式(7)中,当t→∞时,原始地图上每个点的最终状态即为面域示意图。其中偏微分方程(5)的初始条件是ρ为平均属性密度,边界条件为第二类边界条件。
diffusion based method算法的主要目标是多边形的属性均一。当该算法用于城市尺度的格网统计数据时,由于邻接多边形的属性密度差别很大,可能导致算法最终失败,主要表现在当制图范围内的多边形的最大密度和最小密度相差非常大时,需要多次迭代才能得到平均密度,甚至达不到密度均一的要求。现有的解决方法主要是限制迭代次数,而不管是否达到式(1)所指定的限制条件,如Scape Toad软件采用的就是这种方法。然而,这是针对一般多边形统计数据所做的折中方案。对于格网统计数据,本文根据其空间结构的多尺度特征,改进了diffusion based method算法,使其适用于小尺度格网统计数据的面域示意地图制图。
2 Gastner-Newman算法修正 2.1 格网统计数据尺度效应指数格网统计数据在数据形式上与其他格网数据有着相同的等级结构,在内涵上,格网统计数据是统计数据的格网化。统计部门的统计对象通常具有空间延续性和空间分布的不确定性,统计格网数据具有小尺度不确定、大尺度确定的特征。因此,在本研究中,将多尺度格网的尺度特征关系分为限制作用(restriction effect)和表征作用(representation effect)两种类型。如果大尺度数据的空间分布特征决定了小尺度空间分布的特征,则称大尺度数据对小尺度数据有限制作用;反之,则称小尺度数据对大尺度数据有表征作用。多尺度格网的尺度特征关系用尺度效应指 数S来表达:
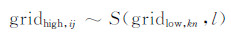
其中,gridlow,kn是gridlow,ij对应的格网,l是尺度因子关系。尺度效应指数S根据统计数据的类型不同可以有不同的表达。
1) 比率型(ratio)、间距型(interval)和周期型(cyclic)统计数据,其数据取值是连续的,不同尺度的主要差别反映在其大尺度综合的平均值与原始数据的差异上,因此 S可以表述为:

2) 命名型(nominal)和次序型(ordinal)统计数据,其大尺度的综合作用体现在小尺度数据内部结构的多样性上。借鉴信息论的二维熵理论,可以设计S为:

 。
2.2 基于尺度效应指数的修正算法
。
2.2 基于尺度效应指数的修正算法
表征和限制关系在反映格网数据大尺度数据分布与小尺度数据分布之间关系的同时,刻划了小尺度格网的内部属性密度的差异状况,可以用来甄别格网统计数据中不适用Gastner-Newman方法的异常格网区域。同时,多尺度格网数据的大尺度格网对小尺度格网有着表征作用,这就意味着大尺度中某个格网的属性数据可以替代小尺度格网相应子格网的属性数据,而不影响其对全局数据分布特征的影响。因此,可以利用这个特征改进Gastner-Newman算法的局部特性,在目标尺度下利用大尺度的数据克服属性密度差别过大而导致算法失败的影响。具体方法如下。
步骤1 :初始化 ρ( g ,0):获取目标尺度levx及levx-1上的属性密度分布格网ρ( g ,0,levx)及ρ( g ,0,levx-1),并将ρ( g ,0,levx)赋值给ρ( g ,0);
步骤2 : 检查ρ( g ,0)格网:计算levx和levx-1的局部尺度效应指数Sij,如果 Sij>thres,则认为ρ( g ,0,levx)在父格网ρij( g ,0,levx-1) (i,j)处产生了局部密度异常,需将ρij( g ,0)的格网尺度升级为levx-1,利用格网ρij( g ,0,levx-1)替代其levx上的子格网,并将ρij( g ,0,levx-1)赋值给ρij( g ,0);
步骤3 :检查ρ( g ,0)中所有尺度为levx-1的格网:获取levx-1格网在levx-2尺度上的父格网,并对levx-2进行类似Step 2中的检查,直到ρ( g ,0)中所有格网均满足阈值要求;
步骤4 :获取格网的节点扩散速度:以ρ( g ,0)为初始条件,第二类边界条件为边界条件求解偏微分方程 ,并计算格网节点扩散速度v(g,t)=-▽ρ/ρ;
,并计算格网节点扩散速度v(g,t)=-▽ρ/ρ;
步骤5 :获取格网节点的最终位置:根据v( g ,t),计算 ,从而确定目标格网每个节点的位置。
,从而确定目标格网每个节点的位置。
需要指出的是,这里对ρ( g ,0) 的尺度修正是局部的而非整体的,这是在保证尺度细节不变的基础上修正原来的算法,使其能满足Gastner-Newman方法对密度的要求。尺度效应指数修正的Gastner-Newman算法,为面域统计特征的社会经济数据可视化提供了一种技术方法,尤其适用于存在局部数据差异较大的人口密度数据的情况。
3 应用实例本文选取2010年全国第六次人口普查获得的北京市常住人口数据为统计数据源,通过对人口数据进行空间化处理,生成了北京市部分区县常住人口的100 m规则格网。但由于城市内部结构差别大,局部100 m格网人口密度差异较大,利用Gastner-Newman算法制作面域示意地图时会导致算法崩溃。
针对上述问题,本文利用基于尺度效应修正的格网数据示意地图算法,对100 m格网人口密度数据进行试验。利用格网统计数据尺度效应指数筛选人口密度异常格网,并根据格网数据的表征作用对异常格网用上级父格网属性值替代,直到100 m人口格网密度数据全部满足条件为止。调用Gastner-Newman算法,生成了北京市分区县100 m格网人口面域示意地图,如图 1所示。

|
| 图 1 北京市部分区县常住人口面域示意地图(2010) Fig. 1 Gridded Population Area Cartogram of Some Districts in Beijing(2010) |
从图 1可以看出,北京市部分区县的人口面域示意地图与100 m格网地图相比,具有较好的可视化效果,揭示了城市内部的人口分布差异特征,体现了城市内部的人口是由城市道路所划分的特点。城市道路特征与城市人口分布的空间关系十分明显。
4 结 语统计数据的地图可视化表达是对统计数据空间特征的还原,为探索和挖掘统计信息提供了良好的方法。为了克服空间参考和地图表达的逻辑不一致性,面域示意地图成为一种可靠的统计数据表达方案。本文采用尺度修正的方法,对局部的密度数据进行修正,使得Gastner-Newman的diffusion based method算法可应用在格网统计数据的可视化应用上。
| [1] | Wang Hailong, Chen Yufen. Research on Cartographic Visualization for Statistical Data[J].Science of Surveying and Mapping, 2009, 32(6):66-68(王海龙,陈毓芬. 统计数据地图可视化扩展研究[J]. 测绘科学,2009,32(6):66-68) |
| [2] | Liao Ke. Modern Cartography[M]. Beijing: Science Press, 2003(廖克. 现代地图学[M]. 北京: 科学出版社, 2003) |
| [3] | Ma Yaofeng. The Principle of Cartography[M]. Beijing: Science Press, 2004(马耀峰.地图学原理[M]. 北京: 科学出版社, 2004) |
| [4] | Dorling D. Area Cartograms: Their Use and Creation[M]. West Sussex: John Wiley & Sons, 2011 |
| [5] | Zhang Xiaohu, Zhong Ershun, Zhang Xun,et al. The Uncertainty of Polygon-based Statistical Data Spatial Analysis: Case of Census Data of Haidian District[J]. Journal of Geo-information Science, 2013, 15(03):369-379 (张小虎,钟耳顺,张珣,等. 多边形统计数据空间分析的不确定性研究——以北京市海淀区人口普查数据为例[J]. 地球信息科学学报,2013, 15(03):369-379) |
| [6] | Du Guoming. Methods and Practices of Spatialization for Statistical Population[M]. Beijing:China Agricultural Press, 2008(杜国明. 人口数据空间化方法与实践[M]. 北京:中国农业出版社,2008) |
| [7] | Ai Tinghua. Maps Adaptable to Represent Spatialcognition[J]. Journal of Remote Sensing, 2008,12(2):347-354(艾廷华. 适宜空间认知结果表达的地图形式[J]. 遥感学报,2008,12(2): 347-354) |
| [8] | Dougenik J A, Chrisman N R, Niemeyer D R. An Algorithm to Construct Continuous Area Cartograms[J]. The Professional Geographer, 1985, 37(1): 75-81 |
| [9] | Gusein-Zade S M, Tikunov V S. A New Technique for Constructing Continuous Cartograms[J]. Cartography and Geographic Information Science, 1993, 20(3):167-173 |
| [10] | House D H, Kocmoud C J. Continuous Cartogram Construction[C]. Visualization 98, NC, USA, 1998 |
| [11] | Tobler W R. Pseudo-cartograms[J]. Cartography and Geographic Information Science, 1986, 13(1): 43-50 |
| [12] | Keim D A, Panse C, Schneidewind J, et al. Visualizing Geographic Information: Visual Points vs Carto Draw[J]. Information Visualization, 2003, 2(1): 58-67 |
| [13] | Keim D A, Panse C, Schafer M, et al. Histoscale: An Efficient Approach for Computing Pseudo Cartograms[C]. The 14th IEEE Visualization 2003 (VIS'03), Washington, USA, 2003 |
| [14] | Gastner M T, Newman M E J. Diffusion-based Method for Producing Density-equalizing Maps[C]. The National Academy of Sciences of the United States of America, USA, 2004 |
| [15] | Heilmann R, Keim D A, Panse C, et al. Recmap: Rectangular Map Approximations in Information Visualization[C]. INFOVIS 2004, Austin, TX, 2004 |
| [16] | Keim D A, Panse C, North S C. Medial-axis-based Cartograms[J]. Computer Graphics and Applications, 2005, 25(3):60-68 |
| [17] | Kreveld M, Speckmann B. On Rectangular Cartograms[J]. Computational Geometry, 2007,37(3): 175-187 |
| [18] | Seemann J. The Atlas of the Real World: Mapping the Way We Live[J]. Cartographic Perspectives, 2012,67(4): 77-80 |
| [19] | Hennig B D. Rediscovering the World: Map Transformations of Human and Physical Space [M]. New York: Springer,2003 |
 2015, Vol. 40
2015, Vol. 40



