文章信息
- 李精忠, 李冬琳
- LI Jingzhong, LI Donglin
- 一种基于汇水区合并的DEM综合方法
- A DEM Generalization by Catchment Area Combination
- 武汉大学学报·信息科学版, 2015, 40(8): 1095-1099
- Geomatics and Information Science of Wuhan University, 2015, 40(8): 1095-1099
- http://dx.doi.org/10.13203/j.whugis20130558
-
文章历史
- 收稿日期: 2013-10-11
DEM综合即由较高分辨率的DEM数据派生出较低分辨率的DEM数据,是多尺度地形表达、分析与应用的关键技术[1],其综合过程需满足地形综合的基本约束,即删除次要地形结构特征、保留主体地形结构特征等。DEM综合是一种面向地理特征的、结构化的空间信息抽象过程,并非简单的数据压缩,传统的基于重采样的分辨率变更方法难以满足高质量DEM生产与应用的要求[2]。
现有的地形综合方法大体可归为三类:(1) 基于光滑滤波器的全局滤波法,全局滤波法通过消除原始数据中的高频部分而达到光滑效果,典型的有低通滤波法[3]和小波分析法[4]等。该类方法没有针对具体地貌形态进行舍弃或简化,仅适用于比例尺跨度较小的综合任务;当比例尺变化幅度较大时,综合结果往往偏离真实的地形结构,达不到“保留主要形态舍弃次要起伏”的综合效果。(2) 消除次要数据点的选择性滤波法,如层次法[5]、重要点法[6]、容忍度法[7]以及三维道格拉斯法[8]等。这些方法的基本思想都是根据邻域信息定义DEM点位的重要性,保留重要性高的,删除重要性低的,该类方法在简化过程中缺乏全局的地形结构特征控制,综合结果容易出现山峰削平、谷地抬升的现象,造成整体地貌骨架一定程度上的失真[9]。(3) 基于地形结构线的结构化综合方法,如文献[10]提出的成组等高线综合方法等,其基本思想是首先提取隐含在复杂等高线图形或规则格网DEM中的地形结构线;然后基于对地形结构线的取舍,完成对成组等高线的化简或规则格网DEM的填充,从而实现地形的综合与化简,这类方法考虑了地形的全局结构,合理使用了地形结 构线,在一定程度上避免了地貌形态的扭曲,但地形结构线所关联的等高线弯曲组、规则格网块往往难以自动确立,需要辅以人工识别。文献[2]提出了一种基于次要谷地特征识别与填充的结构化DEM综合方法,其思想是先识别次要谷地特征,然后对其覆盖区域进行填充。该方法有两个缺陷:(1) 填充区域只考虑次要谷地本身,缺乏对邻近谷地、山脊等高程特征的约束,填充结果在被删除次要谷地的边界处显得较为突兀; (2) 填充过程沿主谷底线(直线段)的法线方向线性填充,使得填充后的等高线沿填充方向平直延伸,与周边等高线不协调。
综合看来,传统的地形综合方法不同程度地关注了地形结构特征在综合过程中的控制作用,但缺乏可操作性的模型与算法将地形实体(如山脊、谷地等)与DEM数据网格点或等高线弯曲关联起来并进行一致化的综合化简。基于此,本文提出一种结构化的、基于汇水区合并的全自动DEM综合方法,该方法利用汇水区将基本地形特征与DEM网格进行关联,使用汇水网络进行全局的地形结构控制,基于水文分析从语义层次评价汇水区的地理重要性,以制图综合的基本原则确定汇水区的取舍,通过汇水区的合并实现DEM的综合。
1 原 理为便于后续论述,先给出汇水区的一般定义。汇水区域,又称集水区域、集水盆地、流域盆地,是指地表径流汇聚到同一出水口过程中所流经的地表区域,是一个相对封闭的地形区域单元。通常,一个完整的汇水区域由多个汇水子区域构成,汇水子区域是地表径流汇聚到某一条支流的地表区域,它的出水口是支流与主流或者支流与支流的汇聚点[11]。汇水区及其子区域剖分的结果反映了谷地系统中各子谷地的集水区域,汇水区域可以将规则分布的,彼此之间毫无联系的DEM网格点划分为一个个具有地理意义的多边形水文单元,即谷地汇水区。谷地汇水区是联系地形单元——谷地,与DEM网格点的纽带。按照结构化地形综合“舍弃次要谷地保留主要谷地”的思想,规则格网DEM综合的对象正是那些次要谷地,而谷地汇水区实现了谷地与DEM网格点的关联。
因此,本文对规则格网DEM综合的基本思路是:首先寻找出隐含在规则网格DEM数据中的谷地特征及其汇水区域,建立起谷地汇水区与DEM网格点之间的有机联系;然后对谷地分支的重要性进行评价,删除次要谷地并合并其汇水区到父亲或兄弟谷地;最后,基于合并的汇水区进行约束内插生成新的,删除次要谷地后的DEM。
基于上述思想,DEM综合的流程是:首先从规则网格DEM中提取汇水区域并进行结构化组织,然后进行谷地选取与汇水区域合并,最后基于合并后的汇水区域对DEM进行综合重构。
1.1 谷地汇水区域的提取与结构化组织本文采用文献[12]的方法提取汇水区域,采用文献[11]的方法提取谷底线网络,采用文献[13]的方法确定谷底线提取过程中的有效汇水量阈值。
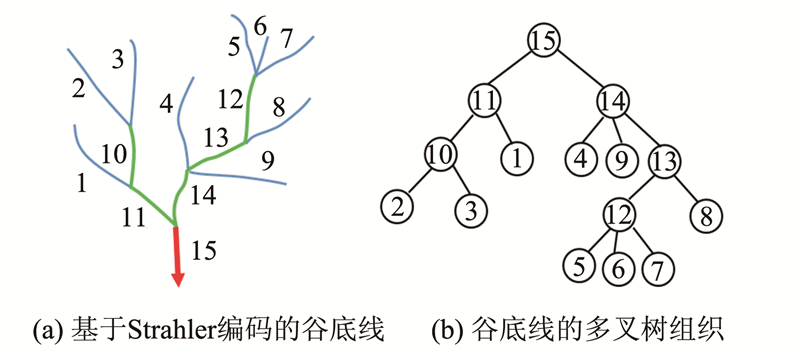
为便于后续对谷地分支的取舍,需要对谷底线网络中各谷地分支进行编码,经典的编码方法有Horton、Strahler、Shreve等[14, 15, 16]。这些方法以水文意义上的重要性作为谷地分支分级编码的依据。本文运用Strahler法则对谷底线进行分级编码。图 1(a)中,谷地分支1~9的Strahler编码为1,分支10~14的Strahler编码为2,分支15的Strahler编码为3。
|
| 图 1 谷底线编码及其多叉树组织 Fig. 1 Valley Line Encoding and Its Structural Organization by Multi-way Tree |
谷地选取是地形综合的重要组成部分,选取数量决定了综合的力度,选取方法决定了综合的质量。通常,选取数量问题可由经典的Tpfer法则确定[17]:
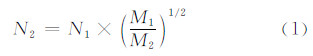
式中,M1、M2分别为资料图比例尺分母和综合图比例尺分母;N1、N2分别为综合前谷地个数和综合后谷地个数,待删除的谷地数目为N1-N2。具体的选取过程既要考虑谷地在流域结构中的地位,又要顾及它本身固有的属性(如长度、汇水面积等)。在此,将谷地删除的对象限定在平面多叉树叶节点层次上,即只删除Strahler级别为1的谷地分支,设其数目为N3。将谷底线树结构中各节点的值f定义为对应谷地汇水区域面积与谷底线长度的乘积,即

式中,ai为谷地的汇水区域面积;li为相应谷地线的长度;i为谷地分支编号。谷地删除操作时,从N3个一级谷地中找出f值最小的,设其编号为a,其父节点为c,分4种情况执行删除操作:(1) 如果a只有一个兄弟节点b,且b为叶子节点,则将b的长度以及a和b的汇水面积一起并入父节点c中,然后删除之;(2) 如果a只有一个兄弟节点b,且b不为叶子节点,则删除b并将b的子节点d、e作为其父节点c的子节点;(3) 如果a有两个及以上的兄弟节点b1、b2等,且所有兄弟节点皆为叶子节点,则删除a并将其汇水面积并入其汇水量最大的兄弟节点,其他节点保持不变;(4) 如果a有两个及以上的兄弟节点b1、b2等,且至少有一个兄弟节点不为叶子节点,则只删除a并将其汇水面积并入非叶子节点的兄弟节点中。然后从剩下N3-1(b为非叶子节点的情况)或者N3-2(b为叶子节点的情况)个候选集中找出f值最小的,按上述规则进行删除。重复此过程直到删除谷地个数达到N1-N2为止。如果所有N3个一级谷地遍历完还未达到待删除谷地的数目N1-N2,则按照删除后的平面结构树对剩下的谷底线重新进行Strahler编码,形成新的1级谷地,并在此基础上进行新一轮的删除,直到删除数目达到N1-N2 为止。
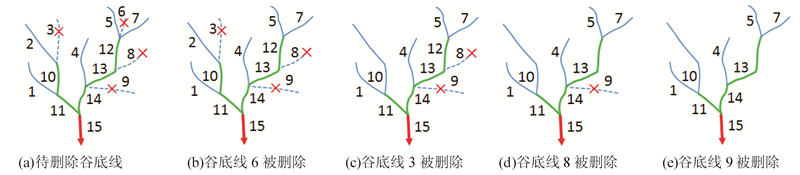
图 2、图 3为谷地删除及汇水区合并示意图。图 2(a)中打叉的节点3、6、8、9将被删除,依据节点f值的排序确定删除顺序为6、3、8、9。首先,删除节点6,满足删除规则(3),故节点6的汇水面积并入其叶子兄弟7中(如图 2(b)、3(a)所示);其次,删除节点3,满足删除规则(1),节点2、3、10合并为一个节点(如图 2(c)、3(b)所示),合并过程中节点2和3的汇水面积被并入其父节点10中,并且节点2的长度也被并入节点10中,节点10的Strahler级别由2降为1;再次,删除节点8,满足删除规则(2),节点8、12、13合并为一个节点(如图 2(d)、3(c)所示),合并过程中节点8和12的汇水面积被并入其父节点13中,节点12的长度被并入13中,并且12的孩子节点5和7提升为其父节点13的孩子节点,节点13的Strahler级别仍然为2;最后,删除节点9,满足删除规则(4)(如图 2(e)、3(d)所示),节点9的汇水面积并入其非叶子节点兄弟13中。删除合并后的平面结构树和谷底线网络如图 2(e)、3(e)所示。
|
| 图 2 谷地删除过程示意图 Fig. 2 Sketch of Valley Line Deletion |

|
| 图 3 谷地删除汇水区域合并示意图 Fig. 3 Sketch of Catchment Area Combination |
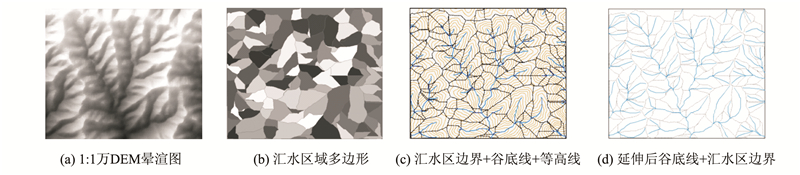
汇水区域多边形边界覆盖了三种主要的地形骨架信息,即山脊线、山顶点和鞍部点,谷底线则覆盖了通常所说的沟谷线。如图 4(c)所示,其中汇水区边界以虚线表示,等高线以细实线表示,谷底线以粗实线表示。由图 4可知,汇水区边界穿越了山脊、山顶和鞍部,谷底线则穿越了谷地。因此,合并后汇水区域多边形边界和删除次要谷地后的谷底线构成了DEM重构时两种重要的约束性元素,提取汇水区域多边形边界和谷底线所穿越的DEM网格点作为新的内插数据源,采用传统的DEM内插方法即可实现指定尺度下DEM的综合重构。
|
| 图 4 原始1∶1万DEM及其对应的汇水区域和谷底线 Fig. 4 Study Area 1∶10 000 DEM and Its Corresponding Catchment Area and Valley Line |
值得注意的是,流水模拟方法在提取谷底线时,地形高处的点因其汇水量较小而常被遗漏,存在谷底线不到源头的问题。如图 4(c)中,1级谷底线都较为短小,离谷地源头相去甚远,这对基于地形骨架线的DEM重构来说是极为不利的。因此,需要对传统的方法稍作改进以提取完备的谷底线。
首先基于D8[18]方向构建流向矩阵和汇水量矩阵,并按一定汇水量阈值提取谷底线,对于所有一级谷底线,按如下两个步骤追踪出其上游谷地源头点:(1) 基于流向矩阵找出所有流向当前谷底点的网格点为候选上游点;(2) 基于汇水量矩阵找出候选点中汇水量最大者为当前点的唯一上游点,若不止一个最大者,则取流向最接近的为上游点。递归此过程直到候选点个数为0为止,则谷底线延伸完毕,谷底线延伸后的效果如图 4(d)所示。
2 实验分析实验数据为国家测绘部门标准化生产的1∶1万规则网格DEM,如图 4(a)所示,数据分辨率为5 m,数据规模为410行×346列,实验区最高高程为1 503 m,最低高程为1 163 m,平均海拔1 340 m。该区域地势东西高、中部低,有典型的谷地发育。实验过程相关算法(如汇水区域提取、谷底线提取、汇水区域合并、谷底线选取、DEM重构等)基于VS2010集成开发环境,采用C#语言编程实现。
从DEM提取谷底线的有效汇水量阈值范围依据文献[13]的方法确定。经反复实验发现,采用汇水量阈值600提取的谷底线和汇水区与原始DEM及对应等高线贴合度较好,在此条件下共提取谷底线116条,汇水区多边形116个。图 4(b)为提取的汇水区域多边形效果图;4(c)为汇水区多边形边界(黑色虚线)、谷底线(粗实线)以及对应等高线的叠加效果图。可见,提取的汇水区完全覆盖地形中的谷地单元。
基于该数据采用本文方法综合生成了1∶2.5万和1∶5万两个比例尺的DEM数据,图 5、图 6分别为1∶2.5万以及1∶5万的综合过程及结果展示,其中图 5(a)、图 6(a)为综合后的DEM晕渲图。为了对比不同尺度综合结果DEM间的差异,1∶2.5万和1∶5万重构后的DEM都采用了与原始1∶1万DEM相同的分辨率(5 m);图 5(b)、图 6(b)为合并后的汇水区域多边形效果图;图 5(c)、图 6(c)为次要谷地删除后的谷底线网络,谷底线选取数量由式(1)确定;图 5(d)、图 6(d)为原始1∶1万等高线,图 5(e)、图 6(e)为采用本文方法综合DEM后派生出的1∶2.5万和1∶5万等高线,图 5(f)、图 6(f)为基于最邻近重采样方法综合DEM后派生出的1∶2.5万和1∶5万等高线,等高距皆为10 m。对比发现,使用重采样方法,无论谷地和山脊大小如何,均同等程度地削减正向、负向地貌,没有顾及地理特征的保持;而本文方法综合后,次要谷地的等高线弯曲呈现成组删除的效果,表示主要谷地源头的等高线弯曲保持较好,与专家手工综合的效果 接近。

|
| 图 5 综合派生后的1∶2.5万DEM及其对应的汇水区域、谷底线和等高线 Fig. 5 The Derived DEM(1∶25 000) and Its Related Catchment Area, Valley Line and Contour |

|
| 图 6 综合派生后的1∶5万DEM及其对应的汇水区域、谷底线和等高线 Fig. 6 Derived DEM(1∶50 000) and Its Related Catchment Area, Valley Line and Contour |
本文提出了一种汇水区合并的结构化DEM综合方法,使用汇水区作为联系谷地概念与DEM网格点的纽带,在谷底线网络的基础上从全局的角度控制谷地取舍,在谷地汇水区合并的基础上进行DEM重构与内插。实验结果表明,本文提出的DEM综合方法,在删除次要谷地特征的同时,较好地保持了主要谷地特征,DEM综合结果符合传统制图综合及空间认知一般规律。
| [1] | Li Zhilin, Zhu Qing. Digital Elevation Model[M]. Wuhan: Wuhan University Press, 2000 (李志林,朱庆. 数字高程模型[M]. 武汉:武汉大学出版社, 2000) |
| [2] | Li Jingzhong, Ai Tinghua, Wang Hong. The DEM Generalization Based on the Filling Valley Coverage[J]. Acta Geodaetica et Cartographica Sinic, 2009, 38(3): 272-275(李精忠, 艾廷华, 王洪.一种基于谷地填充的DEM综合方法[J].测绘学报, 2009, 38(3):272-275) |
| [3] | Burrough P, McDonnell R A. Principles of Geographical Information Systems[M]. Cambridge: Oxford University Press, 1998 |
| [4] | Yang Zuqiao, Guo Qingsheng, Niu Jiping, et al. A Study on Multi-scale DEM Representation and Topographic Feature Line Extraction[J]. Acta Geodaetica et Cartographica Sinic, 2005, 34(2):134-137(杨族桥, 郭庆胜, 牛继平, 等. DEM多尺度表达与地形结构线提取研究[J]. 测绘学报, 2005, 34(2):134-137) |
| [5] | Floriani D, Falcidieno B, Pienovi C. Delaunay Based Representation of Surface Defined over Arbitrarily Shaped Domains[J]. Computer Vision, Graphics and Image Processing, 1985, 32:127-140 |
| [6] | Chen Zitan, Gueyara J A. Systematic Selection of Very Important Points (VIP) from Digital Terrain Model for Constructing Triangular Irregular Networks[C]. Auto-Carto 8, Baltimore, USA, 1987 |
| [7] | Chang K. Introduction to Geographic Information Systems[M]. Boston: McGraw Hill Higher Education, 2004 |
| [8] | Fei Lifan, He Jin. A Three Douglas-peucher Algorithm and Its Application to Automated Generalization of DEMs[J]. International Journal of Geographical Information Science, 2009, 23(6): 703-718 |
| [9] | Dong Youfu, Tang Guoan. Research on Terrain Simplification Using Terrain Significance Information Index from Digital Elevation Model[J]. Geomatics and Information Science of Wuhan University, 2013, 38(3):353-357(董有福, 汤国安. 利用地形信息强度进行DEM地形简化研究[J]. 武汉大学学报·信息科学版, 2013, 38(3): 353-357) |
| [10] | Fei Lifan. Experiments of Group-generalization of Contour Lines on Topographic Maps[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1993, 18(sup):6-21 (费立凡.地形图等高线成组综合的试验[J].武汉测绘科技大学学报,1993,18(增刊):6-21) |
| [11] | Zhu Qing, Zhao Jie, Zhong Zheng, et al. The Extraction of Topographic Patterns Based on Regular Grid DEMs[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(1):77-82 (朱庆,赵杰,钟正,等. 基于规则格网DEM的地形特征提取算法[J]. 测绘学报, 2004, 33(1):77-82) |
| [12] | Zhu Qing,Tian Yixiang,Zhang Yeting. The Extraction of Catchment and Subcatchment from Regular Grid DEMs[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(2):129-133 (朱庆,田一翔,张叶廷. 从规则格网DEM自动提取汇水区域及其子区域的方法[J]. 测绘学报, 2005, 34(2):129-133) |
| [13] | Li Jingzhong, Ai Tinghua, Ke Shu. Effective Flow Accumulation Threshold of Extracting Valley-line from Grid-based Digital Elevation Model[J]. Geomatics and Information Science of Wuhan University, 2012,37(10):1 244-1 247(李精忠,艾廷华,柯舒,等.DEM提取谷地线的有效汇水量阈值范围[J].武汉大学学报.信息科学版,2012,37(10): 1 244-1 247) |
| [14] | Horton R E. Erosion Development of Streams and Drainage Basins: Hydrophysical Approach to Quantitative Morphology[J]. Bulletin of the Geological Society of America, 1945, 56(3):275-370 |
| [15] | Strahler A N. Dynamic Basis of Geomorphology[J]. Bulletin of the Geological Society of America, 1952, 63(7): 923-938 |
| [16] | Shreve R L.Statistical Law of Stream Numbers[J]. Journal of Geology, 1966:74(1): 17-37 |
| [17] | Töpfer R, Pillewizer W. The Principles of Selection: A Means of Cartographic Generalization[J]. The Cartographic Journal,1966, 3 (1):10-16 |
| [18] | O'Callaghan J F, Mark D M. The Extraction of Drainage Networks from Digital Elevation Data [J]. Computer Vision, Graphics and Image Processing,1984, 28(3):323-344 |
 2015, Vol. 40
2015, Vol. 40


