文章信息
- 樊东昊, 朱建军, 周璀
- FAN Donghao, ZHU Jianjun, ZHOU Cui
- 附有限制条件的间接平差的图像配准算法及其应用
- A Method of Image Registration Binding Adjustment of Indirect Observations with Constraints and Its Application
- 武汉大学学报·信息科学版, 2015, 40(8): 1075-1079
- Geomatics and Information Science of Wuhan University, 2015, 40(8): 1075-1079
- http://dx.doi.org/10.13203/j.whugis20130710
-
文章历史
- 收稿日期: 2013-11-26
提高图像分辨率有两种方式,一是提高成像系统的精度和稳定性;二是采取超分辨率重建技术对图像进行后期处理。第一种方式面临成像系统硬件制造的技术问题和高昂的经济代价,因此超分辨率图像重建技术成为当前提高图像分辨率的重要选择。超分辨率图像重建技术是指从序列低分辨率图像中获取高分辨率图像的过程。由于低分辨率图像是对同一场景在不同时间、不同角度或者不同成像系统获取的,因此低分辨率图像存在着不同信息,将这些不同信息进行互补,可以提高图像的分辨率。要利用这些互补信息,必须要在各个低分辨率图像间建立统一的空 间位置关系,即图像配准。图像配准方法可以分为频域配准方法和空域配准方法。Vandewalle频域配准算法[1]仅使用对噪声有很高容忍度的低频部分,可以实现亚像素级的角度配准精度,但由于平移参数的配准精度受到角度配准的影响,导致其整体配准精度较低。Keren空域配准算法[2]在小角度旋转时精度高于Vandewalle配准算法,但是在角度大于6°时其误差较大,且计算复杂度较高。
针对上述问题,本文利用Vandewalle方法和Keren方法各自的优点,根据测量平差中附有限制条件的间接平差原理,提出了一种图像配准改进算法。该改进算法解决了旋转角度过大时Keren配准精度低的问题,提高了图像配准的精度,最后采用POCS算法重建,取得了很好的重建效果。
1 图像配准方法图像配准对不同时间、不同视场或不同成像模式的两幅或多幅图像进行空间变换处理,使得各个图像在空间几何上能够匹配对应。一般的图像配准分为频率域Vandewall 配准算法Keren空间域配准算法[3, 4]。
1.1 Vandewalle配准算法Vandewalle配准算法是基于相位相关法的频率域配准方法。相位相关法源于傅里叶变化平移定理,即信号在空间域的平移对应于频域的相移。利用幅度谱的旋转不变性,将相位相关法扩展到旋转变换求解。假设 f1(x,y)和f2(x,y)代表同一场景的两张低分辨率图像,两者之间存在空间几何关系如式(1):
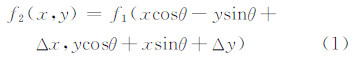
对式(1)两端取傅里叶变换得到式(2):

式中,F1,F2是f1和f2的傅里叶变换形式,由于幅度谱仅与旋转角度有关,定义M1和M2分别为f1(x,y)和f2(x,y)的幅度谱,则满足如下关系:
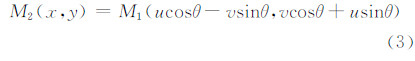
转换为极坐标:
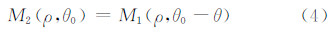
在Vandewalle配准方法中对幅度谱进行了如下积分:

分别求取h1(α)和h2(α),取两者相关度最大情况下的角度,即为图像间的旋转角度。将待配准图像按照计算得到的旋转角度进行旋转,求得待配准图像与参考图像间的相位差,平移参数可以通过相位差的斜率获得。
Vandewalle配准方法使用低分辨率图像的低频信息进行配准,对于含有混淆现象的低分辨率图像,鲁棒性较强,对噪声的敏感度小。Vandewalle算法对于角度配准的精度较高,由于平移配准的精度取决于角度配准的精度,在运动参数较小的情况下精度不如Keren算法高[5, 6]。
1.2 Keren配准算法Keren配准算法基于泰勒级数展开的空间域配准方法。 当式(1)中的θ较小时,对sinθ,cosθ用泰勒级数展开:
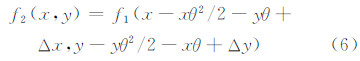
对f1进行二级泰勒展开:
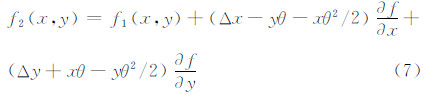
得到误差函数:
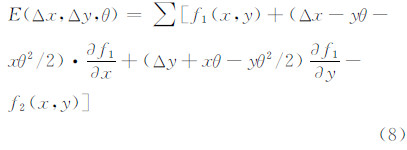
对E关于Δx,Δy,θ分别求偏导,并令偏导等于零:
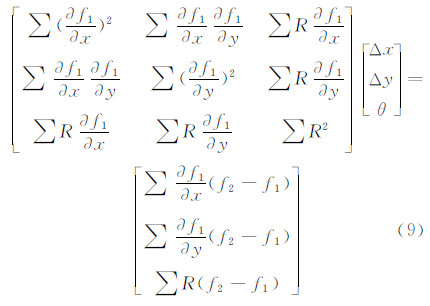
式中,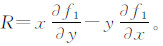
求解线性方程(9)得到平移量Δx、Δy和旋转角度θ。 为了达到亚像素级的精度,Keren算法采用了高斯金字塔算法,即由粗到精的策略来增加Keren配准的精确度。首先对参考图像和待配准图像进行若干次的下采样,获得若干组图像,原图像为金字塔的最顶层。从最底层开始进行配准,将配准得到的参数对上一层的图像进行几何改正后重新进行配准,重复此步骤直至到达最顶层[7, 8]。
1.3 结合附有限制条件的间接平差的配准算法由于Keren算法是基于小角度泰勒级数展开的,实验证明,一般对于6°以内的小角度旋转都能获得较高的配准精度,对于大角度旋转不同视角的遥感图像,Keren配准将带来较大的配准误差,影响图像后期处理。并且Keren配准的计算复杂度与平移大小有关,对于较大的平移,Keren算法的计算量将会大幅增加[9]。
Vandewalle算法在角度配准中有一定的优势,可以实现亚像素级的角度配准,但由于平移配准受到角度配准的较大影响,所以整体精度不如Keren算法高。为了解决上述问题,本文将这两种方法的优点进行集成,提出一种改进的图像配准方法。 即先利用Vandewall配准方法计算的旋转参数和平移参数,将达到亚像素级精度的旋转参数作为Keren算法参数的限制条件,并以平移参数作为初始值,代入Keren配准公式中,依据附有限制条件的间接平差原理,迭代求出平移参数的改正值, 算法的原理如下:
将Vandewalle配准算法得 到的平移参数Δx0,Δy0作为初始值,代入Keren配准算法中(式(7)),按测量平差中的误差方程,式(7)可表示为:
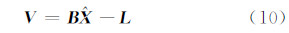
式中,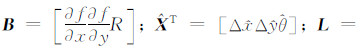
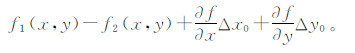 。
。
由于Vandewall配准算法得到的旋转参数θ精度高,因此,直接用所计算的旋转参数θ对Keren配准算法中的该参数进行约束,按测量平差中的附有限制条件的间接平差,平差模型可表示为:

式中,C = 0,0,1 ;Wx=θ。按附有限制条件的间接平差进行计算有
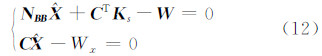
式中,K s是对应于限制条件方程的联系数向量,NBB = B T PB ; W = B T PL 。取权矩阵 P = 1 ,依据式(12)求得参数改正值。
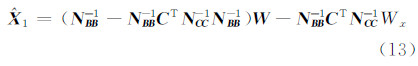
式中,NCC = CN-1BBC T,得到平差值:
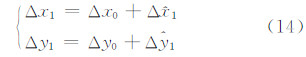
将平差值代入式(10)得到 V ,将平差值Δx1,Δy1替换Δx0,Δy0求解出新参数,重复此步骤直至 V 小于0.01。
将初始平移参数与参数改正值 相加得到最终的平移参数平差值,如式(14)所示,即图像平移的大小。
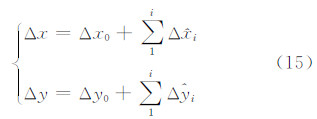
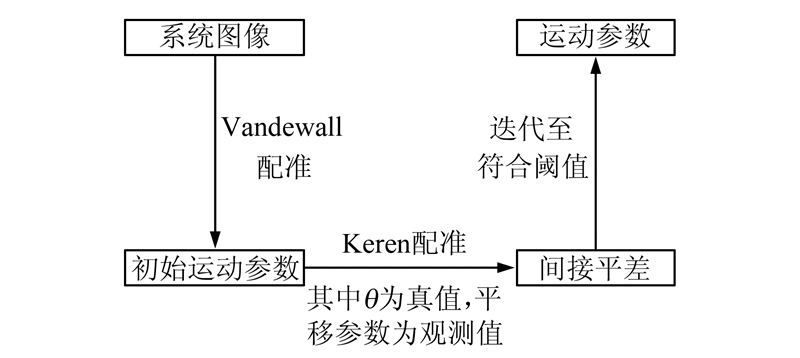
该算法流程如图 1所示。
|
| 图 1 本文算法流程图 Fig. 1 Flowchart of Algorithm |
上述表明,在计算平移参数前,采用亚像素级配准的Vandewalle算法得到的角度参数,避免了角度的泰勒级数展开所带来的误差,且无需使用金字塔算法,避免了计算量的突增。
2 仿真实验与结果分析仿真实验采用了一张512像素×512像素,灰度级为256的图像。根据超分辨率数学模型,对该图像旋转、平移、模糊和降采样及加高斯噪声,模拟产生了5张256像素×256像素的低分辨率图像。以第一张图像为参考图像,其他4张为待配准图像,分别使用Vandewalle算法、Keren算法、文献[10]算法和改进的算法进行配准。根据旋转角度和平移量大小,选用如下4种典型组合:大旋转-大平移;大旋转-小平移;小旋转-大平移;小旋转-小平移进行仿真实验。实验结果见表 1,计算时间见表 2,其中 Δx,Δy,θ为指定的运动参数,μx、μy、μθ为 各个配准运动参数的绝对误差。从表 1中可以看出,4种配准算法都达到了亚像素级的配准精度。Vandewalle算法在角度配准中能够获得较高的配准结果,但平移配准的精度较低,耗时在0.6 s左右。Keren金字塔算法在旋转角度为20°时,其角度配准精度降低,其整体配准精度与Vandewalle算法相比略有提高,耗时随着图像变换参数的增大而迅速增大。文献[10]算法能够获得相对于Keren和Vandewalle算法较高的配准精度,但其耗时较多。采用本文算法,在大角度旋转时的角度配准精度和整体精度都较Keren算法和Vandewalle算法有一定程度的提高;在小角度情况下,该算法也能取得较好的结果,同时耗时较少。
| Δx/像素 | Δy/像素 | θ | Vandewalle算法 | Keren算法 | 文献[10]算法 | 本文算法 | ||||||||
| μx | μy | μθ | μx | μy | μθ | μx | μy | μθ | μx | μy | μθ | |||
| 10.5 | 9.5 | 20° | 0.811 | 0.064 | 0.094 | 0.731 | 0.311 | 0.158 | 0.348 | 0.257 | 0.065 | 0.439 | 0.290 | 0.094 |
| 0.5 | -0.5 | 20° | 0.060 | -0.035 | 0.176 | 0.242 | -0.105 | 0.583 | 0.091 | 0.067 | 0.182 | 0.043 | 0.057 | 0.176 |
| 10.5 | 9.5 | 5° | 0.683 | 0.129 | 0.230 | 0.007 | 0.113 | 0.192 | 0.153 | 0.039 | 0.187 | 0.163 | 0.208 | 0.230 |
| 0.5 | -0.5 | 5° | 0.192 | 0.137 | 0.305 | 0.122 | -0.026 | 0.281 | 0.067 | 0.105 | 0.231 | 0.038 | 0.092 | 0.305 |
| /s | ||||
| 方案 | Vandewalle | Keren | 文献[10] | 本文 |
| 大旋转-大平移 | 0.642 | 1.818 | 2.316 | 1.021 |
| 大旋转-小平移 | 0.718 | 2.233 | 2.269 | 0.937 |
| 小旋转-大平移 | 0.674 | 0.919 | 1.694 | 0.961 |
| 小旋转-小平移 | 0.666 | 0.458 | 1.378 | 0.782 |
为验证该改进算法,采用凸集投影算法POCS方法进行超分辨率图像重建[11, 12],如图 2所示。可以看出,采用本文改进算法配准重建的高分辨率图像与Vandewalle算法、Keren算法配准重建获得的高分辨率图像相比,图像细节有提高。为了能够清楚看出图像细节变化,在整幅图像中选取红色框内的截图进行比较,如图 3所示。本文采用峰值信噪比(PSNR)来衡量图像重建质量,如表 3所示。

|
| 图 2 POCS重建图像 Fig. 2 Reconstructed Image by POCS |

|
| 图 3 重建图像的截图 Fig. 3 Screenshot of Reconstructed Image |
| Vandewalle | Keren算法 | 本文算法 |
| PSNR/db | 18.395 | 20.941 | 22.329 |
图像配准的精度对于超分辨率图像重建的效果有着重要的影响。利用本文算法得到的配准参数的精度高于Vandewalle算法和Keren算法,不仅避免了大角度旋转时,泰勒级数展开所带来的误差,而且减少了计算复杂度。将本文算法应用于超分辨率重建,得到的重建图像的PSNR比Vandewalle算法和Keren算法高出1 db。
| [1] | Vandewalle P, Süsstrunk S, Vetterli M. Supper Resolution Images Reconstructed from Aliased Images[C].SPIE/IS&T Visual Communication and Image Processing Conference, Lugano, Switzerland, 2003 |
| [2] | Keren D, Peleg S, Brada R.Image Sequence Enhancement Using Sub-pixel Displacements[C].Computer Vision and Pattern Recognition, Ann Arbor Mich, USA, 1988 |
| [3] | Fan Chong,Gong Jianya, Zhu Jianjun. POCS Super-resolution Sequence Image Reconstruction Based on Improvement Approach of Keren Registration Method[J]. Computer Engineering and Applications, 2006,36:28-31(范冲,龚健雅,朱建军.基于Keren改进配准算法的POCS超分辨率重建[J].计算机工程与应用, 2006,36:28-31) |
| [4] | Zhi Yuan, Ahrary A, Yan Peimin. Image Registration Based on Genetic Algorithm and Weighted Feature Correspondences[C]. The 13th IEEE International Symposium on Consumer Electronics, Kyoto, Japan, 2009 |
| [5] | Vandewalle P, Ecole P, Sbaiz L, et al. Super-resolution from Unregistered and Totally Aliased Signals Using Subspace Methods[J]. Signal Processing, 2007,55(7):3 687-3 703 |
| [6] | Lin Hui, Liang Liang, Du Peijun, et al. Image Registration Based on Fourier-Mellin Transform[J]. Geomatics and Information Science of Wuhan University, 2012, 37 (6):649-652(林卉,梁亮,杜培军,等.利用Fourier-Mellin变换的遥感图像自动配准[J].武汉大学学报·信息科学版, 2012,37 (6):649-652) |
| [7] | Ma Jun, Jing Weili, Fan Chong. Papoulis-gerchberg Super-resolution Reconstruction Based on Improvement Approach of Keren Registration Method[J]. Bulletin of Surveying and Mapping, 2007,12:14-17(马俊,景维立,范冲.一种基于改进Keren空域配准方法的Papoulis-Gerchberg超分辨重建[J].测绘通报, 2007,12:14-17) |
| [8] | Li Yanhu. Research on Sub-pixel Image Registration Methods with Noise[D]. Chengdu: Southwest Jiaotong University, 2005(李彦虎.亚像素噪声图像配准方法研究[D].成都:西南交通大学,2010) |
| [9] | Fan Chong, Gong Jianya,Zhu Jianjun, et al. An Improvement Approach Based on Keren Sub Pixel Registration Method[C].The 8th International Conference on Signal Processing, IEEE, Beijing,2006 |
| [10] | Li Xiangguo,Ma Xiaochuan. Image Registration Based on Phase-correlation and Keren Algorithm[J]. Microcomputer Applications,2009,30(11):19-13(李相国,马晓川.基于相位相关与Keren算法的图像配准[J].微计算机应用, 2009,30(11):19-23) |
| [11] | Fan Chong,Gong Jianya,Zhu Jianjun.POCS Super-resolution Sequence Image Reconstruction Based on Image Registration Excluded Aliased Frequency Domain[J]. ACTA GEODAETICA et CARTOGRAPHICA SinICA,2006,35(4):358-363(范冲,龚健雅,朱建军.一种基于去混叠影像配准方法的POCS超分辨序列图像重建[J].测绘学报,2006,35(4):358-363) |
| [12] | Tsai R Y, Huang T S. Multiframe Image Restoration and Registration[J]. Advances in Computer Vision and Image Processing, 1984,1:101-106 |
 2015, Vol. 40
2015, Vol. 40



