文章信息
- 赵磊, 陈尔学, 李增元, 冯琦, 李兰, 杨浩
- ZHAO Lei, CHEN Erxue, LI Zengyuan, FENG Qi, LI Lan, YANG Hao
- 基于均值漂移和谱图分割的极化SAR影像分割方法及其评价
- Segmentation of PolSAR Data Based on Mean-Shift and Spectral Graph Partitioning and Its Evaluation
- 武汉大学学报·信息科学版, 2015, 40(8): 1061-1068
- Geomatics and Information Science of Wuhan University, 2015, 40(8): 1061-1068
- http://dx.doi.org/10.13203/j.whugis20130681
-
文章历史
- 收稿日期: 2013-11-13
2. 国家林业局遥感与信息技术重点开放性实验室, 北京, 100091
2. Remote Sensing and Information Technology, State Forestry Administration Key Lab, Beijing 100091, China
极化SAR(PolSAR)是近些年较为前沿的SAR技术,可以通过发射和接收不同极化状态的电磁波探测地面目标,获取目标更为丰富的特征信息[1]。PolSAR影像的分割有助于进一步理解PolSAR影像,是PolSAR影像在分类、目标识别等应用中不可或缺的步骤[2, 3]。但PolSAR独特的数据特点制约了其分割算法的发展。因此,PolSAR影像分割方法一直是PolSAR研究中的焦点和难点。
近年来,许多新理论被应用于PolSAR影像的分割,如马尔科夫随机场、水平集、证据理论、分形理论等[4, 5]。其中,谱图分割由于全局优化和点对聚类的优势成为近年来研究的热点,但其运算时间和空间代价较高[6, 7]。Ersahin等[8]第一次将谱图分割的理论应用于PolSAR影像的分割,并率先实现了基于影像边缘信息的谱图分割方法,但不能充分利用PolSAR的极化信息提取边缘信息进行分割;Liubin等[1]基于Wishart统计分布和假设检验方法提取边缘信息,改进了Ersahin[8]的方法,但仍未能提出有效的方法解决运算代价较大的问题。在谱图分割算法的研究中,目前已经发展出一些方法来解决这个问题。一种是采用采样逼近技术,如文献[9]利用的Nyström采样方法,该方法被公认为谱聚类经典的加速算法,但算法实现较复杂,而且对于信噪比较低的图像效果不理想。另一种是对影像预分割处理,通过减少谱图分割中的节点数量降低运算代价。如文献[10]提出的基于分水岭-谱聚类的SAR影像分割方法,虽然是应用于单极化SAR的灰度影像,但其组合算法的策略仍可借鉴。
鉴于以上分析,本文提出一种基于均值漂移和谱图分割的PolSAR影像分割方法。均值漂移(Mean-Shift)在PolSAR影像分割领域已经有所应用[11, 12],具有快速收敛,抗噪性强等优点,缺点在于分割结果往往过于破碎。本文首先利用均值漂移进行预分割,让其过分割的缺点成为优点,为后续算法提供小的分割区域单元;再利用谱图分割点在聚类和全局优化上的优势完成影像分割;最后,为了验证新方法的性能,将其应用于PolSAR影像的分割,采用改进的精度评价指标评价了分割结果,并分析了不同参数设置对分割精度的影响。
1 理论与方法鉴于均值漂移和谱图分割各自的优缺点,本文提出了二者结合的PolSAR影像分割方法,技术流程如图 1所示。

|
| 图 1 基于均值漂移和谱图分割的PolSAR影像分割技术流程 Fig. 1 Flowchart of Segmentation Based on Mean-Shift and Spectral Graph Partitioning |
均值漂移是一种迭代算法。首先,在特征空间中算出当前特征点的偏移均值,移动该点到其偏移均值处。然后,以此为新的起始点,继续重复上述移动,直到收敛到概率密度函数的模态点为止。
本文将Pauli分解后的三个极化散射分量作为 x r的特征向量。使用式(1)的核函数估计x的分布:
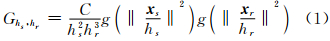
式中,hs和hr分别为空间位置向量和特征向量的核函数窗口值;C为归一化常数;g(·)为非负、非增且连续的函数,如高斯函数。利用均值漂移算法进 行PolSAR影像分割的详细步骤及参数设置原则可参考文献[11]。
1.2 谱图分割算法谱图分割(spectral graph partition,SGP)是建立在谱图理论基础上的一种聚类算法,基于该理论,可以将影像分割转化为图的划分问题[6]:将待分割影像映射为加权无向 图G={V,E}(V:顶点,E:边)。顶点对应影像的每个像元,带权重的边对应像元间的相似性。这样,将影像分割转化为图的最优划分问题。具体过程可以分为三步:(1) 选择合适的影像特征(边缘、灰度、纹理等),建立像元间的相似性度量矩阵,完成影像到图的映射;(2) 选择划分准则,将图划分为一定数量的子图;(3) 将图的划分结果映射到影像空间,完成分割。 因此,首先要提取PolSAR影像的边缘信息,获取分割线索。
1.2.1 边缘信息提取本文进行边缘提取的边缘检测器如图 2所示,共包含4个方向的边缘检测,检测窗口可根据影像实际情况指定(3×3,5×5,7×7,…)。

|
| 图 2 边缘提取的检测器 Fig. 2 Edge Map Calculation Detectors |
若以检测器中心为边缘,则两边区域应存在一定的差异性。这种差异性可基于Wishart统计分布构建假设检验衡量:

式中,Σ i、 Σ j分别为i、j区域的期望协方差矩阵。设Θi、Θj分别为i、j区域的样本协方差矩阵数据集。假设样本间相互独立,i、j区域间是否相似可以通过似然比检验确定。检验统计量[1]如下:
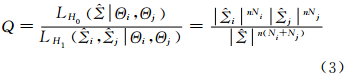
式中,L(·)为不同假设条件下的似然函数; 、 i、 j分别为  、
、 、
、 的最大似然估计量;Ni、Nj分别为i、j区域的样本数量;n为多视视数。如果Q的值较低,则原假设H0将被拒绝。基于这个检验统计量定义两个区域的差异性度量为:
的最大似然估计量;Ni、Nj分别为i、j区域的样本数量;n为多视视数。如果Q的值较低,则原假设H0将被拒绝。基于这个检验统计量定义两个区域的差异性度量为:

式中,Si、Sj分别代表i、j区域;i、j两个区域差异性越大,D(Si,Sj)也越大,边缘强度值也越大。采用式(4)计算每个像元上4个方向的D(Si,Sj),并保留Dmax和它的检测方向。在此基础上进行边缘优化,对于任意像元p,其边缘强度值为Dmax(p),边缘方向为θ*(p)。比较垂直于边缘方向两边像元的边缘强度值,如果Dmax(p)大于等于两边的值,则保留该值,否则,设置为零。
1.2.2 相似性度量矩阵构建边缘信息作为一种有效的影像分割线索,在PolSAR影像谱图分割算法中已经有所应用[1, 8]。但这些算法只适用于从像元出发的情况。本文将试图找到能够代表过分割区域空间位置的某一像元,来解决这一问题,计算方法如图 3所示。
|
| 图 3 过分割区域中心计算 Fig. 3 Positioning of the Center of a Over-segmentation Object |
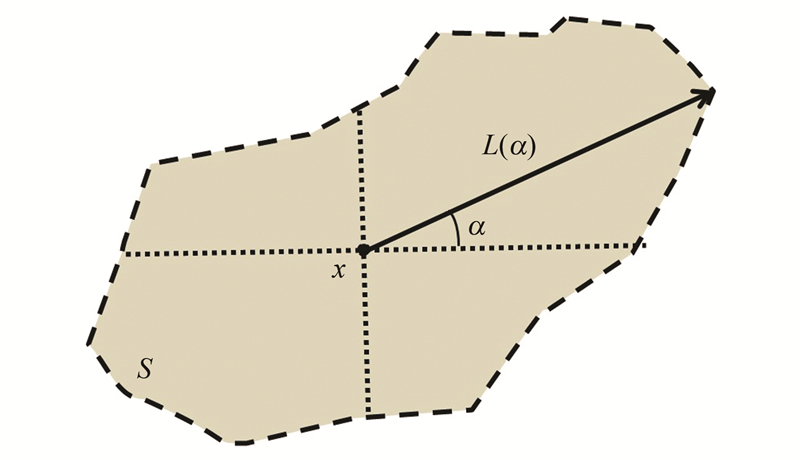
图 3中,灰色多边形为某过分割区域S,x为其内部像元,L(α)为方位角为α时像元x到该区域边界的距离,因此,像元x在过分割区域内的可扩展程度可表示为:
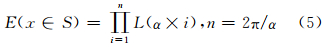
根据式(5),计算区域S内的所有像元的E值,max{E(x∈S)}所对应的像元即为能够代表区域S空间位置的像元。
然后即可利用影像的边缘信息来衡量区域间的相似性程度,如图 4所示。图 4(a)为影像的Pauli RGB显示,S1、S2、S3为3个过分割区域,以及其相应的空间代表性像元p1、p2、p3。两个区域间的相似性度量通过代表性像元间的连线上最大的边缘强度值来体现。如图 4(b)所示,p1和p3之间有明显的边缘存在,其相似性就会较低,即图 4(b)中顶点间边的权重W(p1,p3)较低;同理,W(p1,p2)则较高。因此,定义差异性度量:
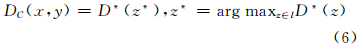

|
| 图 4 基于边缘信息的区域间相似性权重计算 Fig. 4 Illustration of Extracting the Dissimilarity Information from Edge Maps |
式中,D*(·)代表边缘强度值;l是连接像元x和y的直线;z*为该连线上具有最大边缘强度值的像元。通过高斯核函数映射即可完成权重的计算:
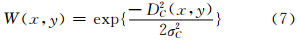
式中,σC为核函数映射的尺度参数。由式(7)便可完成相似性度量矩阵的构建。
1.2.3 归一化割准则谱图分割的划分准则种类繁多,常见的划分准则及其优缺点可参考文献[6]。本文选择应用较为广泛的归一化割准则完成影像分割。假设将一个图划分为两个子图A和B,原来连接A、B后来被删去的边的权重之和在图论中称为割(cut):
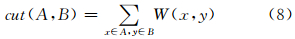
Shi和Malik[13]将式(8)除以表现顶点集大小的度量,完成割的归一化,即为归一化割准则:

式中,V=A∪B;assoc(A,V)代表A中的所有顶点与该图顶点间权重的和。这时,图的划分准则即最小化归一化割Ncut(A,B)。
1.3 分割评价方法鉴于PolSAR影像特殊的统计模型,分割评价中常用的区域间对比度、区域内部一致性等评价指标不再适用。本文将以在遥感影像分割研究中应用较多的正确分割的百分数作为指标,评价PolSAR影像分割结果。陈晓秋等[14]通过累计待评价分割图中的每个区域内与参考分割图重叠的最大面积计算正确分割的百分数。该方法计算出的精度与区域个数相关,分割区域数越多,精度越高。因此,只有当分割区域数相当的情况下,上述分割精度的比较才有意义。但这种比较的公平性难以保障,而且分割精度无法同时反映过分割和欠分割的程度。
本文对上述方法进行改进,计算正确分割的百分数。如图 5所示,虚线区域f为参考图分割区域,与其有重叠的待评价分割区域分别是 a、b、c、d这4个区域。灰色区域e是面积最大的重叠区,其面积为Se。改进方法考虑了区域e在区域d中的面积比例(Se/Sd)。 若该比例很小,则e应属于区域f的欠分割部分,相应像元属于错误分割,不应参与正确分割百分数的计算。因此,本文定义一个反映欠分割程度的参数,欠分割比例(under segmentation ratio,USR):
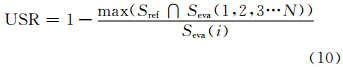

|
| 图 5 分割评价原理示意图 Fig. 5 Illustration Chart of Segmentation Evaluation Principle |
式中,Sref为某参考分割区域面积,Seva为待评价分割区域面积,N为重叠的Seva个数,Seva(i)为与Sref重叠最大的Seva。如图 5所示,USR=1-Se/Sd。依据 USR,即可通过限制欠分割程度计算正确分割的百分数。例如,设置USR=0.2时,只有重叠区域最大且欠分割比例不大于0.2的像元才会被计入正确分割的像元数。这样计算出的分割精度对于影像过分割和欠分割的程度均有所反映,可以更客观地评价分割方法的优劣。
2 实验与分析 2.1 实验数据本文实验采用的数据为2013年6月16日获取的Radarsat-2全极化数据(C-波段),升轨,模式为FQ18,入射角37.56°,方位向、距离向分辨率分别为4.96 m和4.73 m。覆盖区域为内蒙古海拉尔垦区上库力农场依根区域,截取部分农田区域作为实验区域,影像多视处理后大小为312像元×292像元,图 6为影像的Pauli RGB显示。

|
| 图 6 实验区Pauli RGB显示 Fig. 6 Experimental PolSAR Data in Pauli RGB |
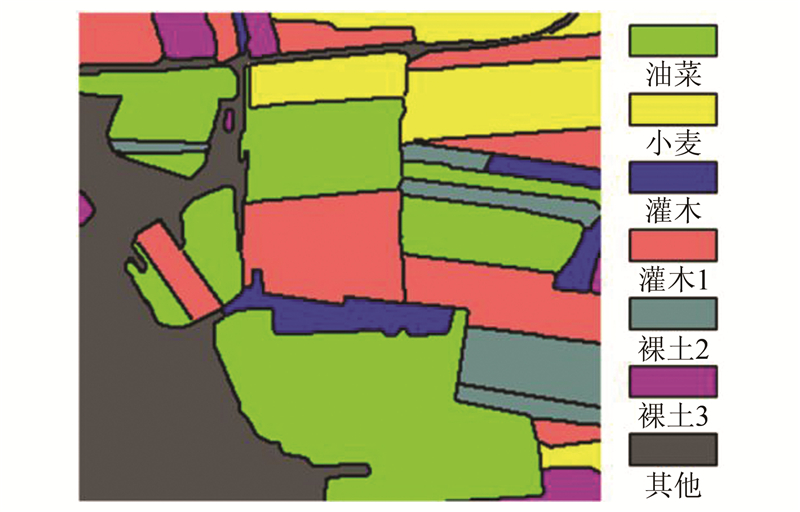
评价分割结果的参考图如图 7所示,通过专家知识和地面真实数据获得。主要步骤包括:(1)首先获取该地区同季节的光学影像,利用ArcGIS 9.3等软件勾绘出地块边界;(2)在Radarsat-2过 境当天,开展同步的土地覆盖类别调查,采用差分GPS设备根据现场实际情况修正勾绘边界,定位记录地块属性;(3)利用ArcGIS 9.3等软件将修正后的边界、地块属性等数据数字化,并进行适当后处理,例如将属于同一类但没有明显边界的地块合并,属于同一类但有明显边界的不予合并;(4)与Radarsat-2影像数据匹配,获得最终的参考分割图。该区域的土地覆盖类别主要包括油菜、小麦、灌木、裸露耕地和其他共5类。其中,裸露耕地因粗糙度、垄向、含水量等因素的影响表现为三种不同的极化反映,因此细分为三类。
|
| 图 7 分割评价参考图 Fig. 7 Reference for Segmentation Evaluation |
经过多视化、Lee滤波(3×3)等数据预处理步骤,首先提取影像的边缘信息,检测器窗口设置为7×7。图 8为边缘粗提取结果;图 9为边缘优化结果。图 10是不同参数设置下的均值漂移的分割结果,分割区域的块数分别为349、173及96。可以看出,单纯尺度的调整无法使均值漂移算法实现全局较优的分割,即便在最大尺度的情况下,图 10中的椭圆黑框区域范围仍处于过分割的状态,而矩形黑框内已经出现了欠分割的情况,由此可见,分割过于破碎是均值漂移难以克服的缺点。

|
| 图 8 边缘粗提取结果 Fig. 8 Raw Result of Edge Map |

|
| 图 9 边缘优化结果 Fig. 9 Optimized Result of Edge Map |

|
| 图 10 不同尺度的均值漂移分割结果 Fig. 10 Segmentation Results of Different Scales Based on Mean-Shift |
选择中等尺度的均值漂移(N=173)结果作为谱图分割的输入。代表性像元的空间位置如图 11中黄色的点所示(α=π/4),可以看到,这些点均处于区域相对中心的位置。

|
| 图 11 过分割区域中心 Fig. 11 Over-segmentation Regional Center |
在上述基础上,构建过分割区域间的相似性度量矩阵,并通过归一化割完成分割。这一步骤中,可以通过设置最终的分割区域个数控制影像分割的尺度。图 12是不同分割区域个数设置的分割结果,其分割细节的表现不同。当区域个数设置为42时,矩形黄色框内的两块裸土没有分割开,设置为48时则被分割开。其主要原因在于,两块裸土间边缘强度较弱,因此在区域个数设置较小时,它们将被合并为一个区域。

|
| 图 12 不同尺度的谱图分割结果 Fig. 12 Segmentation Results of Different Scales Based on SGP |
为了进一步验证本文方法的有效性,使用eCognition图像分割软件中的多尺度分割方法,对该实验区Pauli RGB影像进行了不同尺度的分割,参数设置及分割结果如图 13所示。随着分割尺度的增大,区域个数逐渐减少,过分割现象得到有效缓解(椭圆黑框区域),但是同时,欠分割现象也在逐渐加剧(方形黑框区域)。这也说明了eCognition软件的多尺度分割与均值漂移类似(图 10),在单一尺度设置上很难获得全局最优的分割结果。综合比较图 12及图 13的分割结果,相比之下,本文方法(图 12(b))的分割结果最为优良。不同大小的农田块基本都得到了较好的分割,成为独立的对象,区域一致性好,这为下一步的影像解译奠定了良好的基础。

|
| 图 13 eCognition多尺度分割结果(Sh:形状C:紧致度 Sc:尺度 N:区域个数) Fig. 13 Segmentation Results of Multi-resolution Segmentation Approach Based on eCognition |
算法的运算代价,实验影像为312行×292列,共91 104个像元,若采用传统的基于像元的谱图分割算法,则需通过C91 1042次运算建立91 104 ×91 104大小的相似性矩阵,而本文方法只需C1732次运算建立173×173大小的矩阵,运算空间及时间需求均降低约28万倍。由此可见,均值漂移预分割明显降低了谱图分割算法的运算代价,而谱图算法全局优化的策略也使最终的分割结果优于目前比较流行的算法。
2.3 定量评价与分析为了更客观地评价分割算法,选用定量的方法评价分割结果的优劣。首先,分别选取本文和eCognition多尺度方法较好的分割结果(图 12(b)和图 13(b))进行精度评价;然后,在其基础上,固定尺度外的参数不变,分析分割精度随分割区域个数的变化;最后,分析了均值漂移分割区域个数对分割精度的影响。
经计算,本文方法的分割精度为83.6%,eCognition方法为75.1%(USR=0.3)。图 14是不同方法正确分割像元的分布图。其中白色区域为正确分割的像元。可以看出,eCognition方法的分割精度很大程度上受到分割过于破碎的影响。

|
| 图 14 不同分割方法正确分割像元数分布 Fig. 14 Distribution of Correct Segments Pixels Based on Different Method |
分割精度随USR的变化趋势如图 15所示。分割精度随USR的增大而增大,但本文方法的分割精度始终大于eCognition方法的分割精度。USR=0时,即表明不允许任何欠分割现象,实际分割时几乎不可能出现,因此精度为0;USR=1时,表明对于欠分割不做任何控制,只要与参考图重叠面积最大,则计入正确分割的像元数。

|
| 图 15 分割精度随USR变化趋势 Fig. 15 Segmentation Accuracies According to Different SUR |
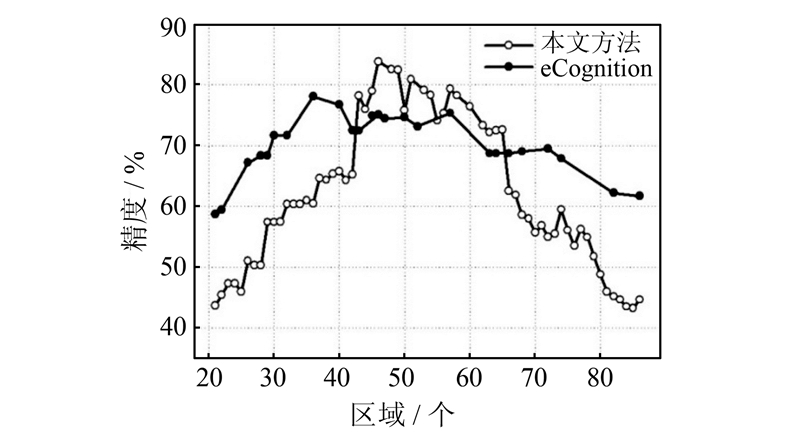
图 16是不同方法分割精度随分割区域个数的变化趋势(USR=0.3)。可以看出,峰值两侧的分割精度均呈下降趋势,这验证了本文改进的分割精度评价指标对过分割和欠分割现象均有反映,克服了以往文献[14]中评价指标的缺陷。分割精度的峰值高于eCognition方法,且在42~65范围内时,精度明显高于eCognition方法;而在曲线两端,eCognition方法的精度要高于本文方法,但这两侧都趋向于不理想的分割结果,精度也较低。
|
| 图 16 分割精度随分割结果区域个数变化趋势 Fig. 16 Segmentation Accuracies According to Different Region Number |
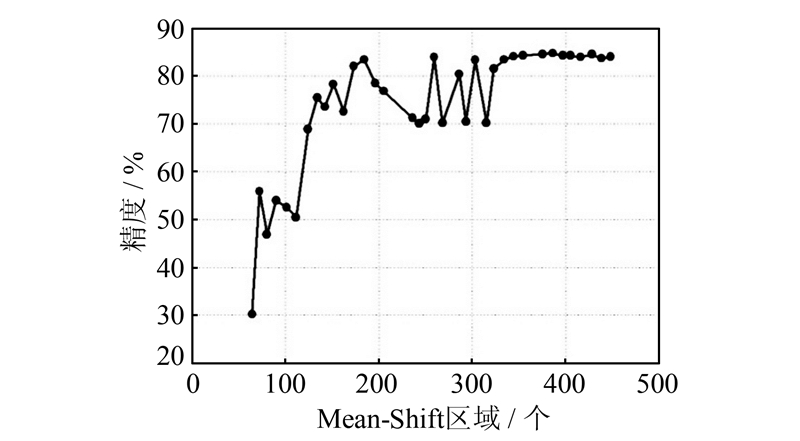
图 17是本文方法分割精度随均值漂移过分割区域个数的变化趋势(其他参数设置与图 12(b)相同)。可以看出,随着过分割区域个数的增加,分割精度整体呈增长趋势,虽然有一定的波动,但在区域个数达到一定数目时趋于稳定。这说明,在利用均值漂移进行过分割时,区域个数不宜过少,在区域个数达到一定数目时(大于320),本文方法会表现出较好的稳健性。
|
| 图 17 分割精度随均值漂移过分割区域个数变化趋势 Fig. 17 Segmentation Accuracies of SGP According to Different Over-segmentation Region Number Based on Mean-Shift |
在谱图分割框架下,本文提出了一种新的基于均值漂移和谱图分割的PolSAR影像分割方法。利用Radarsat-2全极化数据,验证了提出的方法,基于改进的精度评价方法和分割结果参考图,对于本文方法和eCognition的多尺度分割方法进行了定量的精度评价。相关实验表明:(1)本文提出的算法有效实现了PolSAR影像分割,组合算法能够有效降低谱图分割算法的运算代价,得到理想的分割结果;(2)本文分割算法的分割精度要优于eCognition软件的多尺度分割方法,分割结果更趋近于参考图的分割结果;(3)本文提出的改进的分割精度评价方法,可以有效地评价分割结果的优劣,对于过分割和欠分割都能有所反映,可以独立于分割结果的区域个数评价分割精度;(4)在均值漂移过分割区域个数达到一定数目时,本文提出的算法具有较好的稳健性。
本文提出的算法仍存在一定的不足,例如整个分割算法中最优参数选择,算法的适用性,以及是否可引入其他特征等方面,尚需进一步的研究。
| [1] | Liu B, Hu H, Wang H, et al. Superpixel-based Classification with an Adaptive Number of Classes for Polarimetric SAR Images[J]. IEEE Trans. Geosci. Remote Sens., 2013, 51(2): 907-924 |
| [2] | Zhang Jie. Segmentation of Polarimetric Synthetic Aperture Radar[D]. Qingdao:Shandong University of Science and Technology, 2012(张杰. 极化SAR影像的分割[D]. 青岛:山东科技大学, 2012) |
| [3] | Yu Jie, Liu Zhenyu, Yan Qin, et al. Semiautomatic Object-oriented Classification of SAR Images on Multiscale[J]. Geomatics and Information Science of Wuhan University, 2013, 38(3):253-257(余洁, 刘振宇, 燕琴,等. 多尺度下的半自动面向对象SAR影像分类[J]. 武汉大学学报·信息科学版, 2013,38(3):253-257) |
| [4] | Deng Shaoping, Li Pingxiang, Zhang Jixian, et al. Segmentation of Multi-polarized SAR Imagery Based on the Theory of Evidence[J]. Science of Surveying and Mapping, 2011, 36(6): 32-37(邓少平, 李平湘,张继贤,等. 一种基于证据理论的多极化SAR图像分割方法[J]. 测绘科学, 2011,36(6):32-37) |
| [5] | Yang Xin. Study on Segmentation and Classification Algorithm of Polarimetric SAR Images[D]. Chengdu:University of Electronic Science and Technology of China, 2008(杨新. 极化SAR图像的分割和分类算法研究[D]. 成都:电子科技大学, 2008) |
| [6] | You Li.Research on Image Segmentation Method Based on Spectral Clustering[D]. Changsha:National University of Defense Technology, 2011(由里. 基于谱聚类的图像分割方法研究[D]. 长沙:国防科学技术大学, 2011) |
| [7] | Yan Chengxin, Sang Nong, Zhang Tianxu. Survey on Graph Theory Based Image Segmentation Technique[J]. Computer Engineering and Applications, 2006, 5: 11-15(闫成新, 桑农, 张天序. 基于图论的图像分割研究进展[J]. 计算机工程与应用, 2006, 5:11-15) |
| [8] | Ersahin K, Cumming I G, Ward R K. Segmentation and Classification of Polarimetric SAR Data Using Spectral Graph Partitioning[J]. IEEE Trans. Geosci. Remote Sens., 2010, 48(1): 164-174 |
| [9] | Fowlkes C, Belongie S, Chung F, et al. Spectral Grouping Using the Nyström Method[J]. IEEE Trans. Pattern Anal Math Intell, 2004,36(2): 214-225 |
| [10] | Ma Xiuli, Jiao Licheng. SAR Image Segmentation Based on Watershed and Spectral Clustering[J]. Journal of Infrared and Millimeter Waves, 2008,27(6):452-457 (马秀丽, 焦李成. 基于分水岭-谱聚类的SAR图像分割[J].红外与毫米波学报,2008,27(6):452-457) |
| [11] | He W, Jaeger M,Reigber A, et al. Building Extraction from Polarimetricsar Data Using Mean Shift and Conditional Random Fields [C].The 7th European Conference on Synthetic Aperture Radar (EUSAR), Friedrichshafen, Germany,2008 |
| [12] | Zou Tongyuan, Yang Wen, Dai Dengxin, et al. An Unsupervised Classification Method of PolSAR Image[J]. Geomatics and Information Science of Wuhan University, 2009, 34(8): 90-95(邹同元, 杨文,代登信, 等. 一种新的极化SAR图像非监督分类算法研究[J].武汉大学学报·信息科学版, 2009, 34(8): 90-95) |
| [13] | Shi J, Malik J. Normalized Cuts and Image Segmentation[J]. IEEE Trans. Pattern Anal. Mach. Intell., 2000, 22(8): 888-905 |
| [14] | Chen Qiuxiao, Chen Shupeng, Zhou Chenghu. Segmentation Approach for Remote Sensing Images Based on Local Homogeneity Gradient and Its Evaluation[J]. Journal of Remote Sensing, 2006,10(3):357-366(陈秋晓, 陈述彭, 周成虎. 基于局域同质性梯度的遥感图像分割方法及其评价[J]. 遥感学报,2006,10(3):357-366) |
 2015, Vol. 40
2015, Vol. 40



