文章信息
- 段悦, 舒红, 胡泓达, 马国锐
- DUAN Yue, SHU Hong, HU Hongda, MA Guorui
- 全球MODIS气温数据的修正秩克里金插值分析
- Globle Temperature MODIS Data Interpolation with Fixed Rank Kriging
- 武汉大学学报·信息科学版, 2015, 40(8): 1036-1041
- Geomatics and Information Science of Wuhan University, 2015, 40(8): 1036-1041
- http://dx.doi.org/10.13203/j.whugis20140054
-
文章历史
- 收稿日期: 2014-01-16
2. 武汉大学苏州研究院, 江苏 苏州, 215123
2. Suzhou Institute of Wuhan University, Suzhou 215123, China
克里金插值法作为空间最佳线性无偏估计法(best linear unbiased prediction,BLUP)[1, 2],是基于空间属性在空间位置上的变异分布,利用半变异函数确定周围点对待插值点的影响权重以实现待插值点属性估计[3]。该方法综合考虑变量的空间结构性和内在随机性,相对于其他插值预测方法,能够从不完整且含有测量误差等噪声的空间数据中获取最优预测并获得预测均方根误差图[4]。因此,克里金插值法广泛应用于地质学、土壤学[5]、气象学[6]和遥感[7]等地球科学领域。
随着大数据时代的到来,各种空间数据剧增,需要对大量的空间数据进行了分析。研究者在提高插值效率方面做了许多工作[8]。如黄文[9]提出将低高阶结合的插值算法,但该算法仅限在小量级数据的插值应用,当需处理大数据时几乎无法实现。苗莎[10]通过并行和多核平台相结合的方法来提高插值速度,能够处理大量数据,但这对计算机性能要求较高,不利于普及推广。因此,在一般计算机能够达到的运行环境下,如需对数据进行最优无偏估计插值工作,首先需要解决优化克里金方程式中n×n的协方差矩阵求逆的问题。传统克里金法计算复杂度为O(n3),对具有大量数据的克里金方程直接求解,仅上千维的矩阵运算就可导致计算异常缓慢,插值效率极低。修正秩克里金(fixed rank kriging,FRK)算法是近年发展起来的一种新的最优空间估计方法[11, 12],能在降低克里金方法计算复杂度的同时保证克里金法自身优势。该方法中的协方差函数(Σ)具有高度灵活性,并且Σ-1可以通过对一个r×r(r<
目前,由于FRK方法用于气温方面的研究还较少,本文结合全球MODIS气温数据,利用FRK方法进行插值研究并与普通克里金做对比分析。
1 FRK方法 1.1 最优线性无偏空间预测模型{Y( s ): s ∈DS}代表区域化随机变量,Z( s )代表随机变量的观测值,ε( s )为测量误差。于是有:
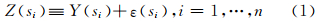
式中 ,ε(·)是一个空间白噪声过程,与Y(·)相互独立,且ε(·)~N(0,σε2vε(·));Y(·)可以拆分为两部分:
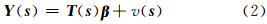
式中,T ( s ) β 是一个与位置相关的趋势项,T (·)≡(T1(·),…,TP(·))'代表已知的p维向量,β 为未知的系数向量;v( s )为一个随机过程,均值为0且0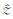 =a0+a1·lon+a2·lat+a3·lat2(lon表示经度,lat表示纬度)时,R2=0.8,拟合程度较好。因此本文中选择 T ( s )=(1,lon,lat,lat2)′,同时 β =(β1,β2,β3,β4)′,使用最小二乘方法拟合趋势项,然后对观测值去除趋势[12]。
=a0+a1·lon+a2·lat+a3·lat2(lon表示经度,lat表示纬度)时,R2=0.8,拟合程度较好。因此本文中选择 T ( s )=(1,lon,lat,lat2)′,同时 β =(β1,β2,β3,β4)′,使用最小二乘方法拟合趋势项,然后对观测值去除趋势[12]。
对于所有 s ∈DS,有:
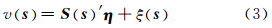
式中,S 为基函数; η 为随机影响向量,假设 η ~Nr(0,K );ξ(·)表示由降维引入的误差,ξ( s )~N(0,σξ2vξ( s )),ξ( s )相互独立且与η不相关,vξ(·)为已知函数。 Shi等[13]和Cressie 等[12]将 S (·)′ η 称为空间随机效应(spatial-random-effects,SRE)模型。由式(1)~(3)可知,
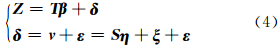
则有:

式中,Σ 代表协方差矩阵; D =σξ2 V ξ+σε2 V ε; V ξ≡diag(vξ(s1),…,vξ(sn)); V ε≡diag(vε(s1),…,vε(sn));函数vξ(·)和vε(·)都假设为已知(可以简单假设 V ξ= I n,V ε= I n)。 此处并没有对空间协方差函数做任何的稳定性或各项同性的假设[14]。式(5)的拆分结构是实现简化计算的关键。此处大规模空间协方差矩阵 Σ 为稀疏矩阵(不存在空间自相关处矩阵元素为0),空间降维转换为矩阵的降秩或者秩的修正。对协方差矩阵 Σ 的降秩在式(5)中体现为将对称正定的高阶协方差矩阵 Σ 分解为低阶矩阵 K和对角矩阵D ,其中高阶到低阶的过度由基函数S实现(基函数将在§1.2中介绍)。
由于我们的兴趣所在是真实值Y(·),而不是带有测量误差的Z(·)过程,所以对于每一个预测s0,s0∈D(无论s0是否为具有观测值的点)都希望能获得Y(s0),参照Cressie[15],给出以下克里金预测Y(s0)的公式:
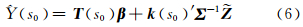
式(6)即为在SRE模型下的FRK预测公式。式(6)中,Σ 由式(5)给出,并且
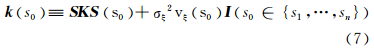
根据Sherman-Morrison-Woodbury[13]公式对 Σ = SKS ′+ D 求逆,有:
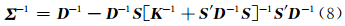
在式(8)中,对高阶(n×n)对称阵 Σ 进行求逆运算,只需要对低阶(r×r)的正定矩阵 K 和高阶(n×n)的对角阵 D 分别求逆,可在很大程度上简化运算,将计算的时间复杂度从O(n3)降为O(r3)。在对每一点进行预测的同时,都可以获取该点上的均方根误差:
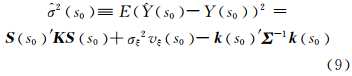
式中,k s0 的值由式(7)给出。
1.2 空间协方差函数空间协方差函数的建立是克里金方法的核心。传统的克里金方法是根据不同滞后距离上的协方差值选择合适的模型来拟合整个区域的协方差函数。而FRK方法在协方差函数的获取方法上有所不同,首先通过一组r维基函数(不要求正交)

来获取不同尺度上的空间相关性,这里 r是固定值。基函数 S 的选择主要从以下几个方面来考虑[16]:首先,基函数的个数r 必须远小于观测数据的个数n,以便对协方差矩阵进行降维,降低计算复杂度。其次,为了能够获取不同尺度上的空间变异性,最好在不同的分辨率上选择基函数。每一分辨率上都存在一组有着相同的平滑度和变程的基函数,且不同分辨率间变程不同。第三,同一尺度上的基函数分布应尽量覆盖整个感兴趣空间。
基函数的选择类型可以有很多种,例如双平方函数(bisquare functions)、小波函数(wawelets)、指示函数(indicator function)、经验正交函数(empirical orthogonal function)、调和函数(harmonic function)等。Cressie和Johannesson[15]建议同一分辨率尺度上的基函数半径等于该分辨率上任意两个基函数中心之间最短距离的1.5倍。
本文采用上述双平方函数作为获取中心点构造基函数的方法,有:

式中,j=1,…,n;vj(l)代表三个不同分辨率下选取的中心点,l=1,2,3,且各分辨率下分别有32、92、272个中心点。通过式(10)可计算得到每一已知点u与每一中心点之间的距离构成的基函数值,分布情况如图 1所示。

|
| 图 1 三个不同尺度上共396个基函数中心的分布情况< Fig. 1 The Locations of the Centers of the 396 Basis Functions of the Three Resolutions |
获取基函数 S 后,对任意的r×r正定矩阵 K ,令
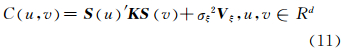
式中,K 和σξ2为需要计算的参数,并且易证C (u,v) 是一个正定的协方差函数[12]。
本文使用Katzfuss等[17]提出的期望最大化(expection-maximization ,EM)算法迭代计算 K 和σξ2的值。 K [0]和σξ2[0]作为迭代初始值:


式中,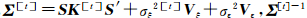 是( Σ [t])-1的简写。通过ArcGIS拟合变异函数得到块金值为零,则将σ2ε取为0。根据Sherman-Morrison-Woodbury公式,由式(8)知对 Σ [t]求逆只需要对r×r的矩阵和对角阵 D =σ2ξ V ξ+σ2ε V ε求逆:
是( Σ [t])-1的简写。通过ArcGIS拟合变异函数得到块金值为零,则将σ2ε取为0。根据Sherman-Morrison-Woodbury公式,由式(8)知对 Σ [t]求逆只需要对r×r的矩阵和对角阵 D =σ2ξ V ξ+σ2ε V ε求逆:
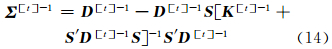
本实验设置的迭代初始值 K [0]=10·var( Z ) · I r,σξ2[0]=0.1·var (Z) ,令θ[t]=[K [t],σ2[t]ξ],ζ=10-6r2≈0.157,按照式(12)~式(14)进行迭代计算,当 θ [t+1]- θ [t]<ζ或者大于预设迭代次数时,迭代过程结束。将结果再次代入式(14)即可计算得到空间协方差函数。
2 实验结果与分析 2.1 实验环境及数据本实验使用的工作站处理器为Intel Core i3 540 3.07 GHz,内存为8 GB。
本文采用2007年5月1日MODIS遥感反演的250 hPa处温度廓线数据进行FRK插值,该数据的空间分辨率为1°×1°,全球共有64 800(180×360)个数据点(部分点位缺失数据)。选择该数据进行实验的主要原因是:(1)该数据点间的空间相关性相对较强;(2)全球范围的数据量较大,便于分析研究计算耗时与使用数据量的变化关系;(3)在该数据中,仅有9 587个空间点(总个数的14.8%)缺失数据,大量的已知数据可以用来检验方法预测的准确性。
图 2为10 000个观测数据点的全球分布图,这些点由所有未缺失数据的样本点中随机选取。

|
| 图 2 观测点数据 Fig. 2 Observation Data |
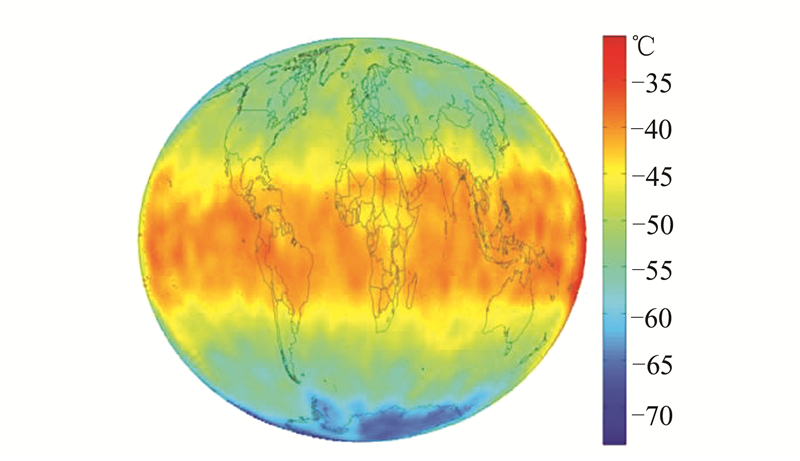
由图 2中的观测点数据对全球64 800个点进行预测,得到的预测结果见图 3。在图 3中,日均温度整体上由赤道向两端逐渐递减,南极气温较北极更低,并且没有出现部分地区突变的情况,过渡比较平滑,非常适用于整体把握上的分析工作。通过交叉验证法对FRK方法插值结果的精度进行评价,获得预测误差的均值、均方根和标准均方根预测误差这三个精度指标值,分别为9.11×10-6 ℃、0.091 7 ℃及1.000 3。当标准均方根预测误差为1时,相同位置的预测值与实际观测值完全吻合。而此处平均误差接近于0,标准均方根误差几近于1,同时均方根值也较小,可见FRK方法能提供较高精度的插值效果,并没有以牺牲精度为代价来换取计算速度的提高。
|
| 图 3 FRK预测值 Fig. 3 The FRK Predictions |
再将FRK和普通克里金(OK)方法在同样的实验数据下进行精度对比试验。考虑到计算机的承受能力,仅在有已知数据的范围(方便将预测值与真实值进行对比)内分别随机选取10 000个点作为观测点数据,20 000个点作为待插值点数据进行实验,对比结果如图 4。二者的插值结果大致相同。观察发现,通过OK方法获得的标准差较大;而在相同实验环境下FRK的标准差较小,精度较高,并且在有观测数据或非常接近观测数据处的标准差非常小,而距离观测点数据较远处标准差相对较大,呈红色。再对比二者的绝对误差图,明显可以看出,OK方法呈现浅蓝色甚至红黄色的区域要多于FRK(根据颜色条浅蓝-黄-红色区域绝对误差逐渐增大)。因此,FRK方法的插值精度相较于OK并没有降低。

|
| 图 4 FRK与OK插值结果对比 Fig. 4 Interpolation Results of FRK and OK |
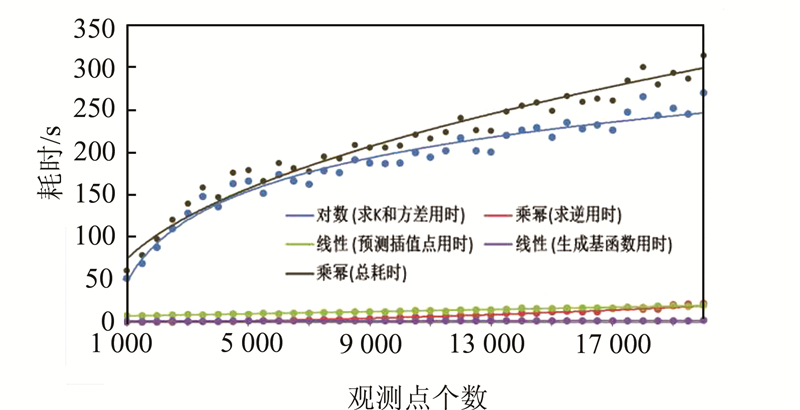
图 5为改变使用的观测点数量对64 800个待插点进行FRK预测时的各运算部分耗时变化情况。其中,基函数的生成以及预测点插值耗时与使用的观测点数量呈缓慢稳定增长的线性关系,求逆用时呈幂函数增长的趋势。但这三部分均为低耗时运算,占用时间不多。整个运算中最为耗时的部分为迭代计算 K 和σξ2 值的运算,且随观测点数量的增加呈现对数增长趋势。迭代的时间消耗主要与选取的初始值和迭代的次数有关,整个实验过程中使用的迭代初始值不变,但随着已知观测点及其数量的改变,迭代的次数会发生一定的变化。在迭代过程占主要运算时间的影响下,总耗时以幂函数形式增长,即随着样本点个数的增大,FRK预测耗时增长趋于平稳。
|
| 图 5 FRK预测耗时随观测点数量变化情况 Fig. 5 Time-consuming of FRK Predict with the Change of the Number of Observations |
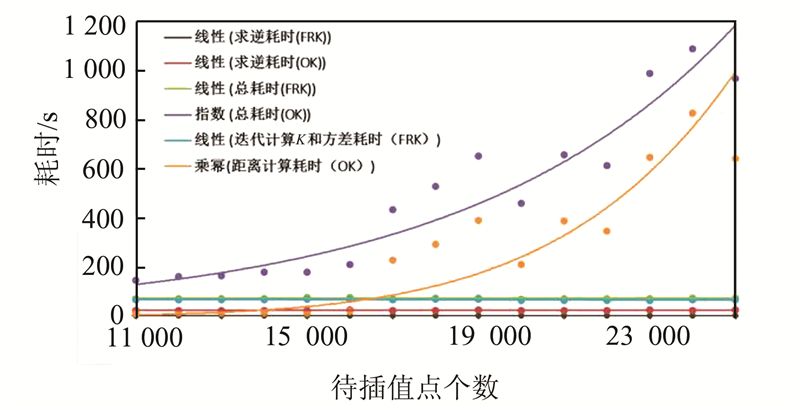
图 6为随机选取6 000个观测点,通过改变待插值点的数量分别对使用FRK和OK方法的求逆、主要耗时运算和整体耗时进行分析。由于仅选取固定数量的观测点,在求逆耗时上二者均基本稳定在2.085 s、23.430 s上;在整体上,FRK方法耗时程度也基本稳定在73 s左右,其中迭代计算 K 和σξ2 部分几乎占用绝大部分的运行时间(约为总耗时的91.4%)。而随着待插值点个数的增加,OK方法耗时呈指数增长,其中距离计算占用时间呈幂函数增长,几乎与总耗时增长保持一致的变化趋势。从主要耗时运算部分来看,FRK方法相对OK方法在算法上具有明显的优越性,即使求逆过程的时间稳定性不变,随着待插值点的增加,迭代计算 K 和σξ2 过程不受影响,但 OK方法中需要的距离计算随之增加(即每增加一个待插值点增加n次距离计算),成功达到了简化计算量,减少耗时的目的。
|
| 图 6 FRK与OK耗时随待插值点数量变化对比 Fig. 6 Time-consuming of FRK Compared with OK with the Change of the Number of Interpolations |
图 7为待插值点数量固定为20 000的情况下,通过改变观测值数量来对比FRK和OK两种方法的耗时程度。由图 7可知,当数据量较小时,OK方法比FRK方法的计算效率更高,耗时相对较少。随着已知观测值数量增加,FRK的求逆、迭代计算和整体耗时均呈幂函数增长,但增长非常平缓。与此同时,OK方法在求逆和整体运算耗时上呈指数趋势迅速增长,其距离计算耗时也以幂函数形式增加。通过对比观察可以发现,随着观测值数量的增加,OK方法的求逆耗时迅速增加,从最初使用3 000个观测点耗时3.404 s到使用9 000个观测点耗时101.244 s;而FRK方法在相同条件下仅从0.598 s增加到4.273 s。由此可知,随着数据量增大,FRK算法相较于OK方法在求逆的计算速度上显著提升。FRK中仅在计算基函数时需要求r×n次两点间距离,而在OK中需要r×n+n×N (N为待估值点数)次距离计算,这导致了OK中大量时间花费在距离的获取上,使用FRK能缩短整体计算时间。

|
| 图 7 FRK与OK耗时随已知观测值数量变化对比 Fig. 7 Time-consuming of FRK Compared with OK with the Change of the Number of Observations |
本文运用FRK方法对全球气温数据进行插值,实验结果显示,FRK方法能提供较高精度的插值效果,并且随数据量增大,耗时程度愈加趋于缓慢平稳增长;而同一环境下使用OK方法的耗时则随数据量增大而呈现指数增长趋势。由此可得到如下结论:(1)FRK能够在不同尺度上获取基函数,使得计算所得协方差矩阵复杂性控制具有一定伸缩性;(2)FRK中将n×n阶对称阵的求逆运算转换为r×r(r n)阶对称阵和n×n阶对角阵求逆的运算,使得计算量大幅减少,速度提高;(3)FRK方法能够在保证预测精度的同时,相较传统克里金方法显著降低计算复杂度,缩短插值时间,该方法在需对大数据进行高效的插值预测时使用能达到较好的效果;(4)FRK比OK更适合对全球性大数据插值计算,能较好地满足一些实时性分析强的应用需求。
n)阶对称阵和n×n阶对角阵求逆的运算,使得计算量大幅减少,速度提高;(3)FRK方法能够在保证预测精度的同时,相较传统克里金方法显著降低计算复杂度,缩短插值时间,该方法在需对大数据进行高效的插值预测时使用能达到较好的效果;(4)FRK比OK更适合对全球性大数据插值计算,能较好地满足一些实时性分析强的应用需求。
| [1] | Brooker P I, Li Xing. Kriging Method[J]. Nonferrous Mines, 1980, 4: 12-15(Brooker P I,李行.克里金法[J].有色矿山, 1980, 4: 12-15) |
| [2] | Davis J C, Sampson R J. Statistics and Data Analysis in Geology[M]. USA: Johu Wiley & Sons Inc, 2002 |
| [3] | Zhang Renduo. Spatial Variation Theory and Application[M]. Beijing:Science Press, 2005(张仁铎.空间变异理论及应用[M].北京:科学出版社, 2005) |
| [4] | Cressie N. The Origins of Kriging[J]. Mathematical Geology, 1990, 22(3): 239-252 |
| [5] | Odeh I O A, McBratney A B, Chittleborough D J. Further Results on Prediction of Soil Properties from Terrain Attributes: Heterotopic Cokriging and Regression-Kriging[J]. Geoderma, 1995, 67(3): 215-226 |
| [6] | Li Sha, Shu Hong, Xu Zhengquan. Interpolation of Temperature Based on Spatial-temporal Kriging[J]. Geomatics and Information Science of Wuhan University, 2012,37(2):237-241(李莎,舒红,徐正全. 利用时空Kriging进行气温插值研究[J]. 武汉大学学报·信息科学版,2012, 37(2):237-241) |
| [7] | Liu Yan, Ruan Huihua, Zhang Pu, et al. Kriging Interpolation of Snow Depth at the North of Tianshan Mountains Assisted by MODIS Data[J]. Geomatics and Information Science of Wuhan University, 2012,37(4):403-405(刘艳,阮惠华,张璞,等. 利用MODIS数据研究天山北麓Kriging雪深插值[J]. 武汉大学学报·信息科学版,2012, 37(4):403-405) |
| [8] | Zhuang Yating, Chen Xunzheng, Fan Shenglong, et al. Study on the Layout of Efficient Arable Land Quality Monitoring Samples Based on Kriging Interpolation Method-Case Study in Jian'ou County[J]. Subtropical Soil and Water Conservation, 2013, 25(2):17-22(庄雅婷,陈训争,范胜龙,等.基于Kriging插值的高效耕地质量监测点布设方式研究——以建瓯市为例[J].亚热带水土保持,2013,25(2):17-22) |
| [9] | Huang Wen. An Efficient Algorithm of Interpolation[J]. Journal of Shanxi University of Technology, 2002,18(1):30-32(黄文.一种高效的插值算法[J].陕西工学院学报,2002,18(1):30-32) |
| [10] | Miao Sha. The Research of Multi-core Parallel Algorithm for Interpolation[D]. Shenyang:Liaoning Normal University, 2011(苗莎.多核并行插值算法的研究[D].沈阳:辽宁师范大学, 2011) |
| [11] | Cressie N, Johannesson G. Spatial Prediction for Massive Datasets[C].The Australian Academy of Science Elizabeth and Frederick White Conference, Australia, 2006 |
| [12] | Cressie N, Johannesson G. Fixed Rank Kriging for Very Large Spatial Data Sets[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2008, 70(1): 209-226 |
| [13] | Shi T, Cressie N. Global Statistical Analysis of MISR Aerosol Data: A Massive Data Product from NASA's Terra Satellite[J]. Environmetrics, 2007, 18(7): 665-680 |
| [14] | Cressie N, Kang E L. High-resolution Digital Soil Mapping: Kriging for Very Large Datasets[M]. Netherlands: Springer, 2010: 49-63 |
| [15] | Cressie N. Statistics for Spatial Data[M]. US: John Wiley & Sons. Inc, 1993 |
| [16] | Woodbury M A. Inverting Modified Matrices[J]. Memorandum Report, 1950, 42: 106 |
| [17] | Katzfuss M, Cressie N. Tutorial on Fixed Rank Kriging (FRK) of CO2 Data[D]. Columbus: The Ohio State University, 2011 |
 2015, Vol. 40
2015, Vol. 40



