文章信息
- 李莹莹, 吴昊, 李旭, 贺杰, 鲍莉
- LI Yingying, WU Hao, LI Xu, HE Jie, BAO Li
- 一种异源主被动遥感图像立体成像技术
- Heterogeneous Stereo Imaging Technology Based on Active and Passive Remote Sensing Data
- 武汉大学学报·信息科学版, 2015, 40(8): 1029-1035
- Geomatics and Information Science of Wuhan University, 2015, 40(8): 1029-1035
- http://dx.doi.org/10.13203/j.whugis20140060
-
文章历史
- 收稿日期: 2014-01-07
随着高分辨率对地观测卫星和传感器平台上高精度导航、定位、姿态等测量技术的重大突破,多源遥感数据的立体成像技术已成为遥感领域的重要发展方向。然而,不同遥感器立体成像的潜力还远未被充分挖掘出来,大量研究仍集中在同源数据的联合处理上,如光学立体像对[1]、SAR 立体像对[2, 3, 4]等。如何最大限度地联合多种主被动遥感数据进行复合式立体成像,摈弃传统同源立体对数据源的苛刻限制,同时保证立体构像产品的精度,是亟待解决的关键问题。目前航天遥感主要有线阵CCD 和SAR 载荷两种类型,其成像机理完全不同,各有优缺点。CCD 分辨率较高,信噪比好,对比度强,但侧摆角度偏小,立体效果有限,受天气和昼夜影响明显;SAR 作为一种主动遥感手段,和CCD相机相比具有全天候、全天时的优势,其特有的侧视特点使得其对高度敏感,但容易产生几何畸变,利用CCD 下视投影可以对其进行辅助校正。
目前国内外遥感领域关于异源立体定位技术的相关研究非常少见,并且局限在基于少量数据的理论验证阶段[5, 6, 7, 8],与工程化应用有较大差距。本文提出一套“异源主被动遥感图像立体成像技术”的实现方案。
1 总体方案及算法模块异源立体成像方案由4个主体技术模块组成:构像参数精化模块、异源同名点自动匹配模块、立体联合解算模块及DEM生成显示模块。具体步骤是,首先分别建立SAR/光学图像的几何构像模型,利用控制点精化计算各自的模型参数;然后进行SAR和光学图像的粗配准、光学特征点的自动提取以及异源图像同名点的自动精匹配;联合SAR和光学构像模型建立立体定位方程组,逐一解算同名点对的地面三维位置;最后对所得到的地面点位置进行三角构网内插,生成规则DEM并完成符合人眼特性的三维影像显示。
1) CCD和SAR图像构像参数精化模块
基于异源图像进行联合立体成像的首要条件是构建图像像点和地面点的精确空间几何关系。光学图像目前基本采用推扫CCD方式,可视为行中心投影图像,建立多中心投影的共线方程模型;SAR图像是斜距构像,方位向运用多普勒频移进行合成处理,可以建立距离-多普勒模型。这两种模型符合光学和SAR严密成像机理,且需要解算的外方位参数较少,非常适合控制点稀少、外方位参数初值精度不高的情况。
为了实现地面点的准确定位,必须从源头上提高SAR和CCD几何模型参数的精度。但是目前星上下传的GPS和姿态精度只能达到百m量级,利用少量地面控制点精化求解模型参数是一种实用而可行的方法。又由于卫星飞行轨道较高,成像视场很小,各外方位元素之间存在很强相关性,极易导致解算法方程病态,必须采用一些特殊的求解算法。本文在CCD构像参数精化中采用线角元素分开迭代算法,在SAR构像参数精化中采用一种谱修正迭代算法。通过上述过程分别建立起各图像像点与地面点间的精确几何成像关系(xi,yi)-(XP,YP,ZP)。
2) 异源图像同名特征自动精匹配模块
光学和SAR图像之间的光谱特性差异显著,造成同一地面特征的像素灰度相关性很低,且SAR图像本身斑噪严重,常规的梯度算子很难反映其边缘轮廓信息[9, 10, 11]。
另外,在实际应用中,由于宽幅遥感影像的尺寸大,匹配计算耗时很大。
因此,本文采用从粗到精的多级匹配策略,首先利用仿射变换进行光学和SAR图像的粗配准,解决两幅图像之间的旋转角度和分辨率不一致的问题;基于Harris算子提取光学图像特征点,以其邻近区域子图像作为匹配模板,提取Sobel特征图像;在SAR粗匹配图像对应的局部搜索范围内用ROA边缘检测算法提取SAR特征图像;最后联合两幅特征图像块进行归一化互相关精匹配,确定出SAR图像的同名点。具体实现如图 1所示。通过以上过程建立各图像同名像点间的对应关系(x1,y1)-(x2,y2)-(xi,yi)。

|
| 图 1 CCD和SAR图像同名点半自动匹配 Fig. 1 Automatic Tie-point Matching of CCD and SAR |
3) 异源遥感联合立体成像模块
联合立体成像过程是指通过同名点匹配建立多幅CCD和SAR图像上同名像点之间的对应关系,利用精化后的几何构像模型分别建立各同名 点和其地面点的精确几何关系,最后汇总所有图像的构像方程建立立体联合定位方程组,解算地面三维位置。由于每幅图像可建立两个构像方程,若图像源数量多于两景,从数学上讲,就是利用4个以上方程求解(XP,YP,ZP)的过程,是可解的。具体过程见§2“立体联合定位原理”。
通过立体联合定位依次获得所有同名点对应的地面三维位置列表后,可以采用分块二次多项式等内插方法生成规则DEM格网,并通过三维到平面坐标转换、地形表面属性显示、侧面处理及消隐处理等功能实现DEM的三维显示。
2 立体联合定位原理本文以两幅CCD和SAR图像为例介绍立体联合定位模型构建解算的基本步骤:
(1)地面点P的CCD图像像点坐标p(x1,y1),建立共线方程模型如式(1)前两式;
(2)地面点P的SAR图像像点坐标p(x2,y2),建立距离多普勒模型如式(1)后两式;
(3)联合点P在所有图像源上的构像方程,以式(1)、式(2)建立其地面位置(XP,YP,ZP)未知的立体定位方程组:

式中,CCD构像参数 ai、bi、ci是像点(x,y)对应扫描线的姿态(φ,ω,κ)构成的方向余弦;外方位元素包括载荷位置 XCS,YCS,ZCS 、姿态及其速率等12个参数,通 过6个以上控制点精化获取。SAR构像参数r0为近地点斜距;λ为波长;Mx为斜距分辨率;fD为多普勒中心频率,可在成像处理中采用杂波锁定算法准确计算;外方位元素包括载荷位置 XSS,YSS,ZSS 、速度 VX,VY,VZ 和加速度等9个参数,通过4个以上控制点精化获取。
按照泰勒级数展开式(1)得到误差方程组:

式中,残差 V =( v1 v2 v3 v4 )T,系数阵

地面坐标改正项为 Δ =( dXP dYP dZP )T,常数项 L =( l1 l2 l3 l4 )T的具体计算为:
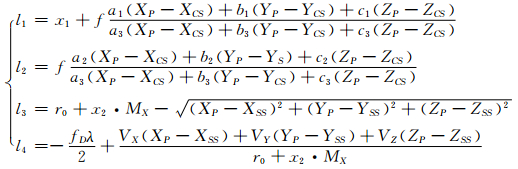
给定初值,对误差方程组(2)采用最小二乘法迭代求解位置改正数 Δ = C T C -1 C T L 。修正地面三维坐标,直到改正数小于某个阈值,迭代终止,得到地面坐标(XP,YP,ZP)。
由于同一个地面点分别在 CCD和SAR 图像上成像,二者本身成像机理完全不同,相关性较弱,构建立体方程组的互补性非常强;并且CCD和SAR 传感器不集成在同一个卫星平台上,即从不同高度、视角观测地面,得到的图像数据将更加立体、全面,具有优良的观测结构,使立体构像系统更加良态;此外,当CCD与SAR 观测光束不存在包含关系时,其地面点的最大交会角相对于同源立体将会增大。这些因素都为异源立体提供了良好的理论基础和应用优势。
3 高程误差传播规律分析异源立体构像复杂,影响因素众多,需要通过全链路误差传播规律理论分析,才能定量描述异源立体获取的三维精度和各可能影响因素的依赖关系。下面以两视立体为例对高程误差进行详细分析。立体方程组(1)为非线性解析式,无法直接进行位置解算和误差分析,必须对其进行简化。不失一般性,假设光学卫星高度为 H,且正下视观测点P,则可假设卫星位置为(0,0,H)。由于姿态均假设为0,所以a1=1,a2=0,a3=0,b1=0,b2=1,b3=0,c1=0,c2=0,c3=1。
如图 2所示,假定SAR和光学卫星在点P处的交会角为θ,得到SAR卫星位置为(0,Htgθ,H),斜距为H/cosθ,即r0+x2·MX=H/cosθ。在这种构型下,SAR卫星的速度主要为VX,VY=VZ=0。那么方程组(1)可以简化为:
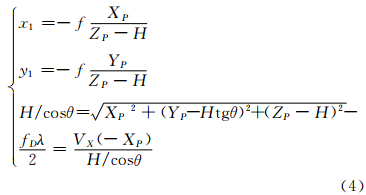

|
| 图 2 异源立体像对的简化几何关系 Fig. 2 Geometry of Heterogeneous Stereo Image Pair |
联合求解可以得到:
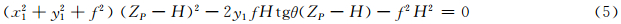

根据误差传播定律,得出高程误差为:
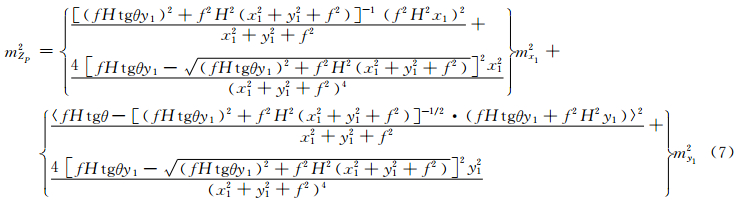
从上述公式可得到以下结论:
1) 复合立体高程精度主要由同名点坐标量测误差决定,而量测误差和图像分辨率、匹配精度密切相关。在分辨率一定的情况下,在坡度起伏较大区域,SAR图像叠掩现象严重,会引起同名点匹配误差增大,进而高程精度恶化。
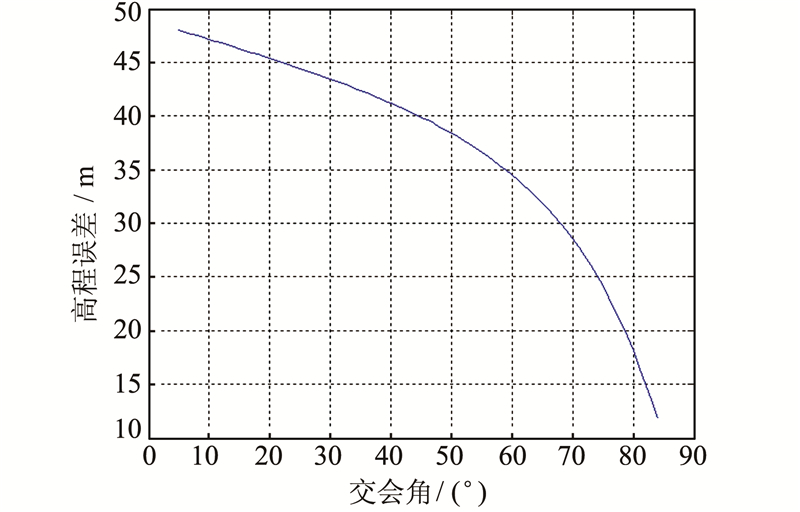
2) 交会角θ的大小会直接影响高程精度,交会角一般和基高比正相关。图 3显示了根据式(7)仿真得出的不同交会角输入条件下的高程精度变化情况,与传统摄影测量中立体交会角越大,则高程定位精度越好的变化趋势是一致的。
|
| 图 3 高程精度随图像交会角变化图 Fig. 3 Height Precision Variation with Image Contact Angle |
3) 前两项结论均是在卫星状态参数(高度H、交会角θ等)测量无误的理想前提下得出的,实际上,受控制点选取误差、成像模型局限等因素影响,得到的精化轨道参量与真实值存在一定偏差,这些也会直接导致高程误差的加大。
4 试验结果及分析采用Cosmo-Skymed 3 m分辨率的SAR图像和IKONOS 1 m分辨率的CCD图像进行了立体成像精度试验。取具有代表性的8组图像对,涵盖北京、台湾、日本、韩国等地区的平原、丘陵、山区三种地貌类型,高程跨度在0~2 000 m左右,以及同向(SAR降轨)和反向 (SAR升轨)两种相对拍摄位置(图 4)。图像上地势错落有致,包含有一定数量的道路、建筑、沟渠等特征地物,每组像对的重叠面积大小均不相同,立体交会角在14 °~63 °之间。

|
| 图 4 反向和同向像对的相对位置示意 Fig. 4 Relative Position of Inverse and Same Direction Pair |
CCD图像的线元素迭代终止阈值设置为前后两次迭代差值小于0.01,角元素阈值设置为小于1.0×10-8,迭代次数均可在10次以内终止。SAR图像的终止阈值设置为前后两次迭代差值小于0.1,迭代次数可保持在5次以内。
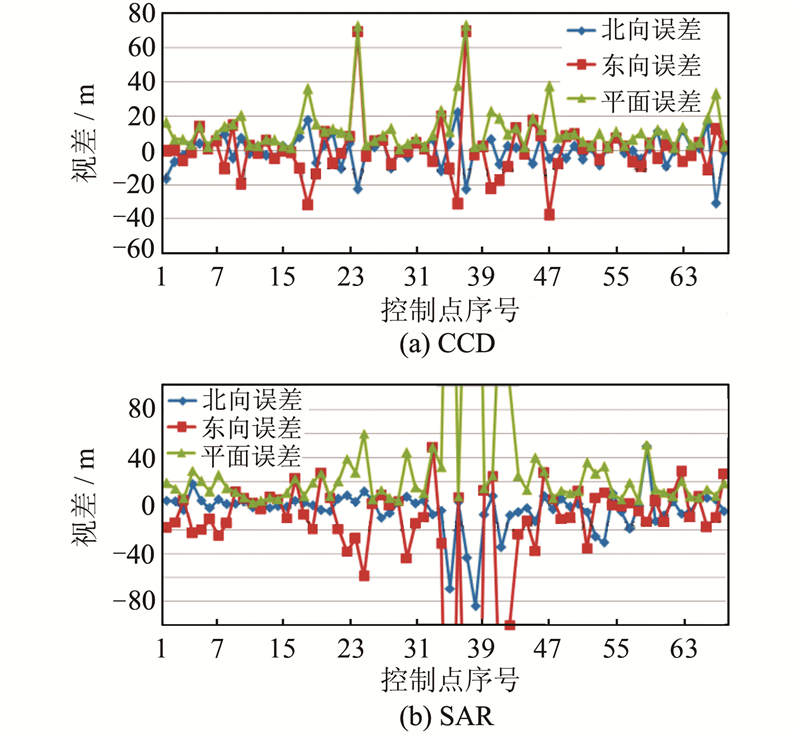
通过计算控制点残差来间接衡量精化获取的轨道参数精度。如图 5所示,CCD控制点残差基本保持在20 m内,表明CCD模型参数精度是比较高的。SAR控制点残差基本在40 m以内,地势起伏较大地区残差明显增加,部分异常点(图 5(b))予以剔除。分析较大残差出现的主要原因,一方面由于卫星成像机理复杂,模型拟合精度有限,而SAR为侧视成像,受地形变化影响较大,引起个别残差出现较大波动;另一方面由于控制点是人工选取,特别是SAR图像地物判读比较困难,不可避免地带有一定的偶然误差。
|
| 图 5 CCD和SAR轨道参数精化后的控制点残差 Fig. 5 Residual Error of Ground Control Points on CCD and SAR Images After Parameter Refinement |
本文实验环境为Intel Xeon W3520,主频2.67 GHz。CCD特征模板设置为128像素×128像素,SAR图像候选区域设置为192像素×192像素,单点平均匹配时间为1 s左右。获取的特征点数随区域大小和特征地物密集程度不同,1 m分辨率200 km2范围图像特征点数通常在几千个左右。反复实验发现,ROA滑动窗大小设置为9像素×9像素时边缘提取的效果最好。图 6给出了对同地区CCD和SAR图像用Sobel和ROA算子进行边缘提取的结果。可以看出,ROA算子提取的边界清楚、细致,且与CCD边缘图像轮廓非常相似。

|
| 图 6 提取CCD边缘 Fig. 6 Sobel and ROA Edge Extraction of CCD and SAR |
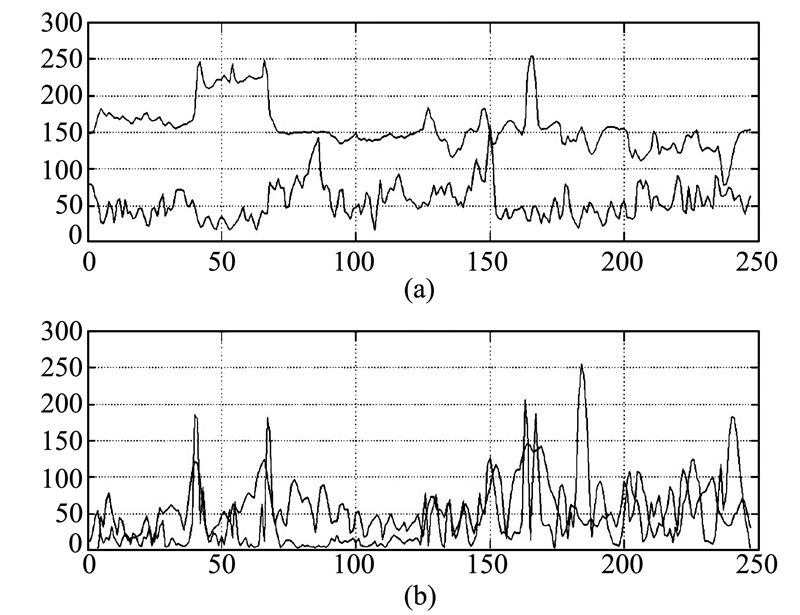
从一维上对比观察原始图像和其边缘特征图像的某一行(图 7),可以看出,在原始灰度图像上,除了在150附近的两个峰值有重合迹象外,其他部分都是混乱的。而经过边缘提取后,相同行的边缘图趋势基本一致。
|
| 图 7 SAR和CCD图像一维灰度对比和梯度对比 Fig. 7 One-Dimensional Gray and Grad Contrast Between SAR and CCD Images |
为了检验同名点提取的精度,拼合CCD和SAR图像相邻子块得到一幅新图像(图 8),进行定性的目视检验。图 8中深浅程度不同的方块分别是SAR和CCD图像子块。可以看出,各种地物(河流、道路、建筑和田块)在相邻图像块接缝处连接十分自然平滑,没有拼接错位,匹配精度较高。此外进行了匹配精度的定量检查,根据同名像素坐标计算坐标差,经过统计,匹配精度可达0.863 9个CCD像元。

|
| 图 8 分别提取SAR和CCD子块交错拼合的图像 Fig. 8 Mosaic Image Composed by SAR and CCD Slice |
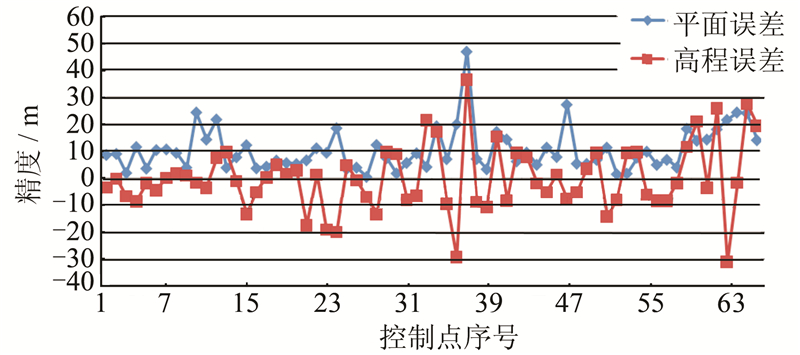
按照上述步骤,在8组像对中随机抽取若干同名点计算其三维位置,将其与参考地图中该点的真实位置作比较,同名点的选取涵盖了整景图像的高程区间。图 9显示了这些同名点的平面和高程误差,精度基本保持在25 m以内。虽然某些SAR图像由于地形起伏较大引起控制点残差恶化(图 5),但是在图 9中这些像对的同名点误差并未偏差太大,原因是在立体联合解算过程中,CCD图像的垂直下视投影构像在一定程度上校正了SAR图像的侧视畸变。
|
| 图 9 检查点的立体定位精度统计结果 Fig. 9 Stereo Positioning RMS of Check Points |
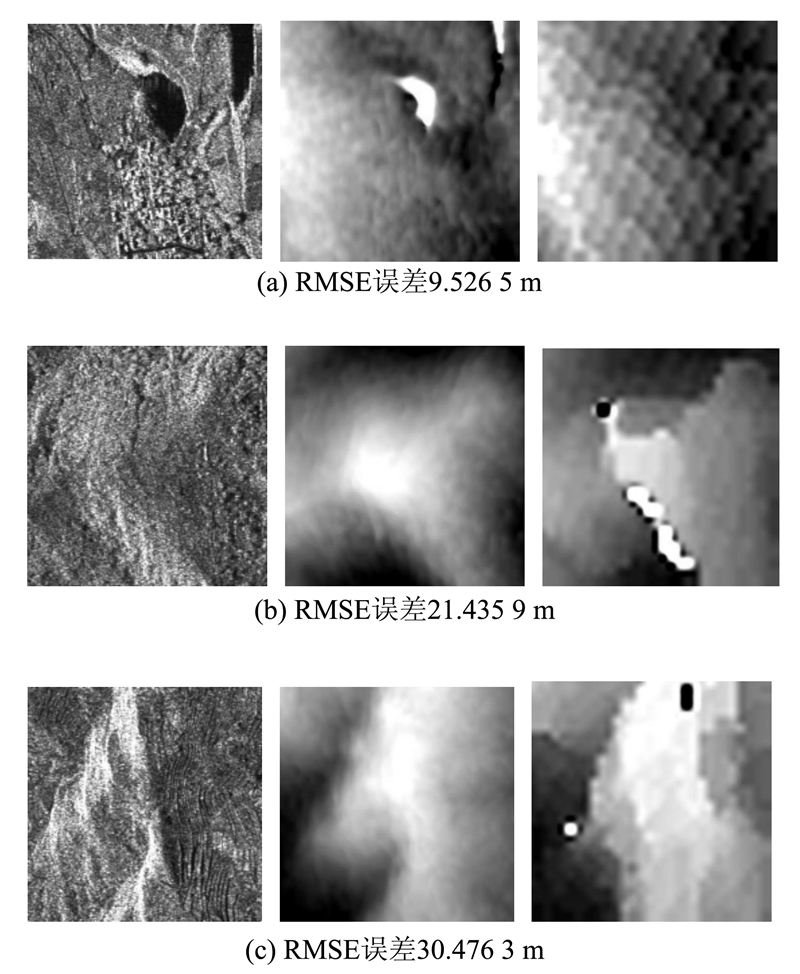
我们随机选取不同地形地貌的三幅300像素×300像素小块图像,计算它们的DEM,将其与参考DEM灰度图比较以便直观显示其精度差异,如图 10所示。此处采用RMSE作为DEM精度评价模型:
|
| 图 10 SAR图像、参考DEM、计算DEM(从左到右)对比 Fig. 10 Contrast of SAR, Reference DEM and Result DEM(from Left to Right) |
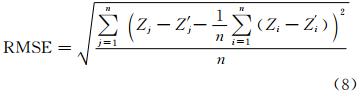
式中,Zi和Z′i分别为参考DEM高程值和本文解算高程值;n 为检查点的数量,减去系统误差后的随机误差才能真实地反映算法的效果。
从DEM灰度显示结果和精度计算结果看出,解算的精度随地形陡峭程度增加而降低,这与式(7)的理论推导完全一致。得出的DEM走向基本与实际DEM吻合,具体数据偏离不大,证明了本方案的可行性。图 10中成片的黑点和白点代表部分点解算不收敛,在DEM计算结果中表示为0或者很大的数,这根本上是由于异源图像匹配错误,让一对毫无关系的点构成立体定位方程组,导致无法得到正确的解造成的。
以覆盖日本、韩国的两组像对为例,基于自动解算出的同名点三维位置列表,完成重叠区域的DEM内插生成和三维显示。图 11代表了起伏程度不同的丘陵和山区地物类型,结果DEM走向与实际DEM基本吻合。解算中出现了部分点不收敛的情况,我们用周围的点对它进行插值以消除。与图 10中的平面显示相比而言,立体影像可以很清晰地显示出地形起伏情况,地面的粗糙情况和细节变化也更加直观。

|
| 图 11 山区立体成像显示 Fig. 11 Stereo Imaging Display of Mountain Area |
本文提出一套异源主被动遥感图像立体成像技术方案,完成从输入原始CCD和SAR数据到输出目标区域立体影像的全流程半自动化处理。在进行算法理论研究的同时,利用大量1 m CCD和3 m SAR卫星图像全面验证了立体成像方案的可行性和精度。试验结果证明,本方案对构像数据源要求宽松,任何有重叠区域、不限时相、不同类型图像均可作为输入,在满足一定交会角度的前提下,可以获得平面20 m以内,高程30 m以内的定位精度。此外在地形起伏较大区域或者异源图像分辨率差异巨大的条件下,同名点匹配精度下降尤其明显,会直接影响立体解算精度,这将是我们后续研究要着重考虑的问题。
| [1] | Zhang Yongjun. Orientation of Remote Sensing Image Pairs from Different Orbits[J]. Geomatics and Information Science of Wuhan University, 2003, 28(5): 521-524(张永军. 异轨遥感立体像对外方位元素的求解算法[J]. 武汉大学学报·信息科学版,2003, 28(5): 521-524) |
| [2] | Edwards E. Evaluation of Space Intersection Strategy for Use with Stereoscopic SAR Imagery over Developing Countries [M]. Austria:Salzburg, 2004 |
| [3] | Song S, Sohn G. An Efficient 3D Positioning Method from Satellite Synthetic Aperture Radar Images [M]. Berlin:Springer,2006 |
| [4] | Liu Jun. High Precision Stereo Positioning of IKONOS Satellite Images Based on RPC Model [J]. Bulletin of Surveying and Mapping,2004, 9: 1-4 (刘军. 基于RPC模型的IKONOS卫星影像高精度立体定位[J].测绘通报,2004, 9: 1-4) |
| [5] | Raggam J. Mathematical Aspects of Multi-sensor Stereo Mapping [C]. IGARSS, Greenbelt, Maryland, 1990 |
| [6] | Toutin T. Stereo-mapping with SPOT-P and ERS-1 SAR Images [J]. International Journal of Remote Sensing,2000, 21(8): 1 657-1 674 |
| [7] | Jordi I. On the Possibility of Automatic Multisensor Image Registration [J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(10): 2 104-2 120 |
| [8] | Xing Shuai. Combined Stereo Location Among Multi-sensor Remote Sensing Images[J]. Geomatics and Information Science of Wuhan University, 2009, 34(5): 522-526 (邢帅. 多源遥感影像"复合式"立体定位的研究[J].武汉大学学报·信息科学版,2009, 34(5): 522-526) |
| [9] | Peng Wen. Research on Some Key Techniques in Medical Image Registration Based on Features [D]. Hangzhou:Zhejiang University, 2007 (彭文. 基于特征的医学图像配准中若干关键技术的研究[D]. 杭州:浙江大学, 2007) |
| [10] | Wang Lei. Feature-based Automatic Registration for SAR and Optical Remote Sensing Images[J]. Journal of Harbin Institute of Technology,2005, 37(1): 22-25 (王磊. 基于特征的SAR图像与光学图像自动配准[J]. 哈尔滨工业大学学报, 2005, 37(1): 22-25) |
| [11] | Johnson H, Consistent G E. Landmark and Iintensity-based Image Registration [J]. IEEE Transactions on Medical Imaging, 2002, 21(5): 450-461 |
 2015, Vol. 40
2015, Vol. 40


