文章信息
- 张胜军, 李建成, 褚永海, 孔祥雪
- ZHANG Shengjun, LI Jiancheng, CHU Yonghai, KONG Xiangxue
- 基于Cryosat和Jason1GM数据的垂线偏差计算与分析
- Calculation and Analysis of the Deflection of Vertical Derived from Cryosat and Jason1 GM Data
- 武汉大学学报·信息科学版, 2015, 40(8): 1012-1017
- Geomatics and Information Science of Wuhan University, 2015, 40(8): 1012-1017
- http://dx.doi.org/10.13203/j.whugis20130796
-
文章历史
- 收稿日期: 2013-12-18
垂线偏差是地球科学计算中的重要数据,通常用南北向分量和东西向分量表示。在卫星测高反演海洋重力场的研究过程中,国内外学者提出由沿轨垂线偏差替代海表面高度作为“新”观测量的方法[1, 2, 3],可以显著削弱径向轨道误差等长波长误差项而无须进行交叉点平差。基于“新”观测量或原始测高数据信息可以确定垂线偏差的方向分量信息,但是存在两个问题:一是测高数据在海冰覆盖、近岸以及岛屿周边海域的数据精度低,相当数量的测高数据被编辑准则剔除,造成这些区域存在数据空白[4, 5];二是卫星轨道设计造成中低纬度海域测高数据分辨率低于高纬度[6],且测高数据确定的垂线偏差南北分量精度优于东西分量[7, 8]。
波形重跟踪可以提升受干扰的回波波形测高精度,是改进近岸及海冰覆盖海域重力场反演精度的有效方法[9, 10, 11, 12]。Cryosat卫星拥有低分辨率模式(low resolution model,LRM)、合成孔径雷达(Synthetic Aperture Radar,SAR)和SIN三种工作模式,在地理环境较复杂的区域通过工作模式切换可以保证数据分辨率和精度。因此,联合波形重跟踪技术和新型测高数据,是填补近岸、岛屿以及海冰覆盖海域数据空白的有效手段。重复周期分别为406.5 d和369 d的Jason1大地测量任务数据和Cryosat数据为中低纬度海域提供了更好的数据覆盖率,有望解决不同纬度分辨率不精的问题,进一步改进海洋重力场的反演精度[13]。Jason1卫星和Cryosat卫星轨道倾角分别为66°和92°,前者更加接近确定垂线偏差的理想设计[7],后者近极轨的设计刚好与前者互补。垂线偏差与海洋重力场反演精度密切相关,Cryosat和Jason1大地测量任务数据为对比分析不同轨道倾角测高数据计算垂线偏差提供了前提条件。
综合上述考虑,本文使用Jason1大地测量任务波形数据和Cryosat数据,基于沿轨重采样提升数据密度,顾及海面时变信号以及海面稳态动力地形的影响,计算并对比分析了低、中、高纬度示例区域内的垂线偏差东西向和南北向分量。
1 数据选取与处理本文联合使用轨道倾角分别为66°和92°的Jason1和Cryosat数据,前者采用大地测量任务阶段的数据,分别选定菲律宾群岛及周边海域(区域1)、渤海及黄海部分海域(区域2)、鄂霍次克海东北部海域(区域3)作为低、中、高纬度示例区域,对比研究不同纬度区域内确定的垂线偏差南北向和东西向分量。
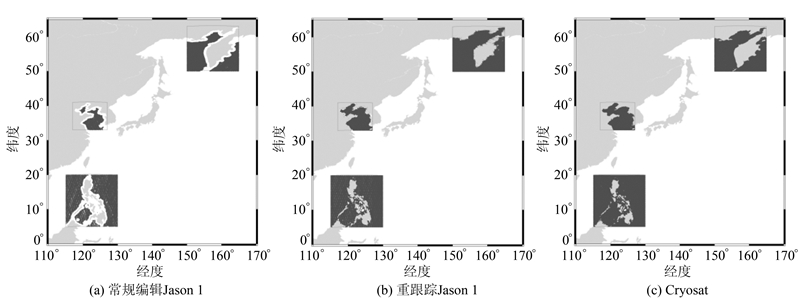
选定的示例海域中,区域1内岛屿众多且地理环境复杂,Cryosat在该区域内全部为LRM测量模式;区域2三面被陆地包围且多为浅水区,该区域内Cryosat数据的SAR测量模式约占三分之二;区域3内测高数据受海冰影响大,SAR测量模式约占三分之一,其余为LRM测量模式。研究区域内,如果采用常规的数据编辑准则,在近岸及岛屿周边海域,大量Jason1大地测量任务数据被剔除(图1(a)),通过波形重跟踪处理,可以对大部分剔除数据进行恢复。
|
| 图 1 研究区域数据分布 Fig. 1 Data Distribution in Research Area |
本文选择顾及多个上升沿的改进阈值法[14]重跟踪处理Jason1波形。相比常规编辑准则剔除的情况,示例区域内波形重跟踪处理后的数据记录数显著提升,详见表1。顾及沿轨数据分辨率和数据精度,统一将重跟踪处理后的Jason1和Cryosat 20 Hz数据沿轨重采样为5 Hz。
| 区域1 (5°N~20°N, 115°E~130°E) | 区域2(33°N~41°N, 117°E~127°E) | 区域3(50°N~63°N, 150°E~165°E) | ||
| Jason1 | 数据类型 | SGDR | SGDR | SGDR |
| 周期范围 | 500~529 | 500~529 | 500~529 | |
| 时间范围 | 2012.5~2013.6 | 2012.5~2013.6 | 2012.5~2013.6 | |
| 示例交叉点 | (12.003°N,125.795°E) | (35.332°N,125.379°E) | (60.416°N, 159.283°E) | |
| 示例交角 | 41.457° | 62.729° | 140.13° | |
| 常规编辑后记录数 | 269 165 | 43 870 | 200 005 | |
| 重跟踪后记录数 | 398 631 | 87 395 | 340 847 | |
| CLS10模型剔除点 | 13 247 | 7 086 | 18 210 | |
| 高斯平滑剔除点数 | 9 902 | 1 208 | 13 262 | |
| 可靠数据记录数 | 375 482 | 79 101 | 309 375 | |
| Cryosat | 数据类型 | GDR | GDR | GDR |
| 周期范围 | 4~6 | 4~6 | 4~6 | |
| 时间范围 | 2012.2~|2013.6 | 2012.2~2013.6 | 2012.2~2013.6 | |
| 示例交叉点 | (12.239°N,118.406°E) | (35.831°N,124.258°E) | (60.426°N,158.178°E) | |
| 示例交角 | 12.058° | 13.964° | 24.168° | |
| LRM模式比例/% | 100.0 | 35.44 | 67.83 | |
| SAR模式比例/% | 0.0 | 64.56 | 32.17 | |
| CLS10 模型剔除点 | 4 672 | 2 902 | 13 034 | |
| 高斯平滑剔除点数 | 12 672 | 2 805 | 10 979 | |
| 可靠数据记录数 | 512 086 | 119 191 | 377 080 |
重跟踪处理恢复出一定数量包含粗差的Jason1数据,采用三种沿轨数据质量控制方法:一是三倍中误差准则沿轨剔除;二是选取CLS10平均海平面模型插值出沿轨离散点平均海面高,并剔除不符值大于3 m的数据点;三是基于邻近数据点由高斯函数计算沿轨离散点处的海面高预测值,剔除不符值大于0.5 m的数据点。经过数据质量控制后,研究区域内波形重跟踪恢复的数据量约为常规编辑准则筛选数据量的39%、80%和54%,数据质量控制剔除数据量详见表1。
表1还统计了示例弧段之间的夹角。可以看出,相同纬度带内的Jason1弧段轨道夹角明显大于Cryosat,表明在沿轨飞行过程中Jason1卫星可以感应到更多的垂线偏差东西向分量信息,而Cryosat数据对于南北分量的垂线偏差更加敏感。因此,Cryosat和Jason1大地测量任务数据具有一定的互补性,有望作为现有测高数据的有力补充,提高海洋重力场模型反演的精度水平。
1.2 海面地形效应削弱在计算垂线偏差之前,沿轨海面高数据需要考虑海面地形的影响,获取沿轨大地水准面高。海面地形分为时不变和时变两部分考虑,其中前者对应的海面稳态地形采用DOT2008A模型计算。
为了削弱时变海面地形的影响,采用时间范围相对应的Jason2数据(Cycle131~183)计算海表面高度异常值,选取5 d和150 km作为时间和空间相关尺度,通过距离加权计算出Jason1沿轨离散点处的海表面高度异常值进行改正。需要注意的是,Jason1和Jason2数据采用相同的参考椭球,而Cryosat数据采用不同的参考椭球,需要考虑参考椭球改正[15]。
为了评价顾及海面地形时变效应的抑制效果,表2统计了改正前后研究区域内的交叉点不符值统计信息。其中Jason1和Cryosat交叉点不符值均方根大都明显减小,表明采用时空对应的Jason2数据可以有效削弱时变海面地形部分。区域3由于常年有海冰覆盖,该处理的作用效果不明显。
| /m | |||||||||
| 区域1-交叉点 | 区域2-交叉点 | 区域3-交叉点 | |||||||
| 个数 | 改正前 | 改正后 | 个数 | 改正前 | 改正后 | 个数 | 改正前 | 改正后 | |
| Jason1 | 22 120 | 0.221 | 0.196 | 6 470 | 0.192 | 0.165 | 47 964 | 0.259 | 0.252 |
| Cryosat | 19 019 | 0.177 | 0.145 | 4 309 | 0.253 | 0.232 | 19 425 | 0.296 | 0.292 |
垂线偏差计算有多种方法,Sandwell提出联合升降弧段沿轨数据点的位置、时间和大地水准面高信息,求解交叉点处的垂线偏差方向分量[7]。该方法计算垂线偏差理论严密,在交叉点处计算的垂线偏差精度较高,但受限于交叉点分布密度。
本文采用Sandwell方法分别确定三个示例区域内交叉点处的垂线偏差分量,与EGM2008模型的检核如表3所示。由检核结果可以看出,测高数据直接计算的垂线偏差南北向分量优于东西向分量,且Cryosat数据确定的垂线偏差方向分量精度差异更大;Jason1确定的垂线偏差东西分量精度优于Cryosat,表明较低的轨道倾角有助于改进垂线偏差东西分量精度。三个研究区域内Jason1确定的交叉点个数分别为22 120、6 470和47 964,而Cryosat交叉点个数分别为19 019、4 305和19 425,难以满足确定高分辨率网格化垂线偏差的密度要求。
| /角秒 | |||||||||
| /arc sec | |||||||||
| 区域 | 方向 | Jason1 | Cryosat | ||||||
| MIN | MAX | MEAN | RMS | MIN | MAX | MEAN | RMS | ||
| 1 | 北 | -24.494 | 54.616 | 0.109 | 1.953 | -20.928 | 25.841 | 0.091 | 1.894 |
| 东 | -57.461 | 48.076 | -0.182 | 3.297 | -93.856 | 98.839 | -0.177 | 6.021 | |
| 2 | 北 | -12.549 | 10.142 | 0.046 | 1.102 | -14.013 | 9.006 | -0.120 | 1.469 |
| 东 | -13.494 | 21.792 | -0.267 | 1.919 | -37.006 | 35.994 | 0.117 | 7.867 | |
| 3 | 北 | -28.900 | 26.541 | 0.013 | 1.942 | -21.936 | 55.178 | -0.083 | 1.818 |
| 东 | -32.753 | 34.195 | -0.060 | 2.083 | -41.517 | 41.659 | 0.117 | 7.905 | |
为了确定高分辨率的网格化垂线偏差,Olgiati方法基于沿轨数据点解算,可以满足密度要求[16]。但该方法需要顾及交叉点沿轨插值的误差。Hwang提出加权最小二乘法,将垂线偏差分量计算和网格化两步合并,联合满足搜索范围的离散点沿轨垂线偏差和方位角信息,直接确定网格点处垂线偏差的南北和东西方向分量,既满足了数据点密度要求,又简化了求解过程[17]。
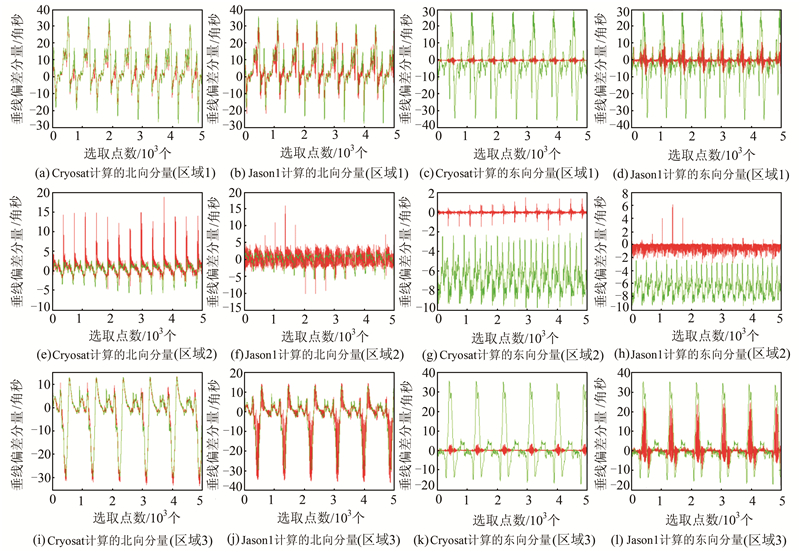
为了直观地对比不同轨道倾角测高数据反演垂线偏差分量的区别,本文不引入参考模型场,直接基于Jason1和Cryosat测高数据计算沿轨垂线偏差,根据加权最小二乘法列观测方程,通过最小范数逆的方法解决秩亏问题,计算三个示例区域内1′×1′的垂线偏差分量,选择EGM2008模型进行检核,见图2和表4。
|
| 图 2 测高数据直接反演垂线偏差(红)与EGM2008模型(绿)的检核 Fig. 2 Comparison Between EGM2008(Green) and Deflection of the Vertical Derived Directly from Altimetry(Red) |
| /角秒 | |||||||||
| /arc sec | |||||||||
| 区域 | 方向 | Jason1 | Cryosat | ||||||
| MIN | MAX | MEAN | RMS | MIN | MAX | MEAN | RMS | ||
| 1 | 北 | -41.289 | 52.558 | 0.462 | 3.024 | -39.125 | 28.945 | 0.144 | 2.408 |
| 东 | -50.842 | 76.463 | -3.693 | 8.784 | -51.119 | 76.953 | -3.784 | 9.075 | |
| 2 | 北 | -64.020 | 39.133 | 0.232 | 1.675 | -21.084 | 31.547 | -0.132 | 1.679 |
| 东 | -31.019 | 35.112 | -6.334 | 1.839 | -13.504 | 0.501 | -6.886 | 1.892 | |
| 3 | 北 | -39.289 | 41.112 | -0.422 | 4.377 | -39.165 | 97.278 | -0.103 | 1.964 |
| 东 | -44.653 | 62.983 | 1.570 | 8.572 | -41.827 | 62.900 | 2.064 | 9.607 | |
从图2和表4可以看出,基于测高数据直接确定的垂线偏差南北向分量显著优于东西向分量,这是由于加权最小二乘法基于沿轨垂线偏差及方位角计算垂线偏差,测高数据的沿轨方位角往往很小,因而反演与沿轨方位角正弦相关的东西分量比较不敏感。而Jason1数据计算的垂线偏差东西向分量显著优于Cryosat数据,较低轨道倾角的测高数据沿轨方位角和地面轨迹夹角较大,可以反映更多的垂线偏差东西向分量信息。区域2内的垂线偏差分量计算结果较差,直接基于测高数据计算的结果与EGM2008模型之间存在系统性偏差,且反演信息变化规律性不明显;分析模型结果发现该区域垂线偏差分量变化较平缓,测高数据感应到的垂线偏差东西分量信息特别微弱。
2.3 基于移去-恢复过程的加权最小二乘法测高数据包含的低阶重力场信息精度低于重力场模型,引入一定阶次的重力场模型作为参考场,基于移去-恢复过程可以有效提升计算精度。本文采用250阶的GOCO03S模型作为参考场,基于沿轨加权最小二乘法和最小范数逆方法解算示例区域内的残余垂线偏差分量,恢复参考模型值,得到1′×1′的垂线偏差分量并与EGM2008模型值进行检核,详见表5。
| /角秒 | |||||||||
| /arc sec | |||||||||
| 区域 | 方向 | Jason1 | Cryosat | GOCO03S | |||||
| MEAN | RMS | MEAN | RMS | MEAN | RMS | ||||
| 1 | 北 | 0.124 | 2.707 | 0.098 | 2.269 | -0.006 | 4.034 | ||
| 东 | 0.065 | 5.337 | 0.137 | 5.548 | -0.012 | 5.880 | |||
| 2 | 北 | 0.080 | 1.710 | -0.133 | 1.660 | -0.013 | 1.753 | ||
| 东 | -0.081 | 1.616 | -0.002 | 1.442 | -0.004 | 1.911 | |||
| 3 | 北 | -0.000 2 | 2.361 | -0.094 | 1.839 | 0.002 | 3.463 | ||
| 东 | 0.029 | 3.527 | 0.046 | 3.664 | 0.008 | 3.887 | |||
由表5可以看出,基于测高数据和移去-恢复过程计算的垂线偏差两个方向的精度均优于参考重力场模型以及直接由测高数据反演的垂线偏差分量,移去-恢复过程还可有效消除区域2内直接由测高数据计算出现的系统偏移。因此,联合测高数据和重力场模型可以确定精度更优的垂线偏差方向分量。
3 结 语369 d重复周期的Cryosat数据以及大地测量任务的Jason1测高数据均具有较高的数据分辨率,通过波形重跟踪处理可以有效解决常规编辑准则在近岸及岛屿周边海域剔除Jason1数据过度的问题。基于时空对应的Jason2数据,有效削弱了Jason1和Cryosat测高数据的时变海面地形部分的影响。
对比使用Sandwell方法和加权最小二乘配置法,基于Jason1和Cryosat数据计算了研究海域内交叉点或网格点处的垂线偏差方向分量。通过与EGM2008模型检核表明,Jason1数据有助于改进垂线偏差东西向分量的确定,联合不同轨道倾角测高数据可以提升垂线偏差计算精度,而引入重力场模型作为参考场可以进一步改进垂线偏差解算。
| [1] | Haxby W F, Karner G D, Labrecque J L,et al. Digital Images of Combined Oceanic and Continental Data Sets and Their Use in Tectonic Studies[J]. EOS, Transactions,1983,64:995-1 004 |
| [2] | Sandwell D T, McAdoo D C. Marine Gravity of the Southern Ocean and Antarctic Margin from Geosat[J]. Journal of Geophysical Research, 1990,93(B9): 10 389 -10 396 |
| [3] | Li Jiancheng , Ning Jinsheng, Chen Junyong, et al. Determination of Gravity Anomalies over the South China Sea by Combination of TOPEX/Poseidon, ERS2 and Geosat Altimeter Data[J]. Acta Geodaetica et Cartographica Sinca, 2001, 30(3):197-202(李建成,宁津生,陈俊勇,等. 联合Topex/Poseidon,ERS-2和Geosat卫星测高资料确定中国近海重力异常[J]. 测绘学报, 2001, 30(3):197-202) |
| [4] | Sarrailh M, Balmino G, Doublet D. The Arctic and Antarctic Oceans Gravity Field from ERS1 Altimetric Data[C]. International Association of Geodesy Symposia, Tokyo, Japan, 1996 |
| [5] | Hwang C,Hsu H Y, Deng Xiaoli. Marine Gravity Anomaly from Satellite Altimetry: A Comparison of Methods Over Shallow Waters[C]. International Association of Geodesy Symposia, Matera, Italy, 2003 |
| [6] | McAdoo D C, Marks K M. Gravity Fields of the Southern Ocean from Geosat Data[J]. Journal of Geophysical Research, 1992,97(B3):3 247-3 260 |
| [7] | Sandwell D, Smith W H F. Marine Gravity Anomaly from Geosat and ERS-1 Satellite Altimetry[J]. Journal of Geophysical Research, 1997,102(B5):10 039-10 054 |
| [8] | Wang Hubiao, Wang Yong, Lu Yang. High Precision Vertical Deflection over China Marginal Sea and Global Sea Derived from Multi-satellite Altimeter[J]. Geomatics and Information Science of Wuhan University, 2007,32(9): 770-773(王虎彪,王勇,陆洋. 联合多种测高数据确定中国边缘海及全球海域的垂线偏差[J]. 武汉大学学报·信息科学版, 2007,32(9):770-773) |
| [9] | Bao Lifeng, Lu Yang, Wang Yong. Improved Retracking Algorithm for Oceanic Altimeter Waveforms[J]. Progress in Natural Science, 2009,19:195-203 |
| [10] | Yang Yuande, Hwang C, Hsu Hungjui, et al. A Subwaveform Threshold Retracker for ERS-1 Altimetry: A Case Study in the Antarctic Ocean[J]. Computer& Geosciences(2011), doi:10.1016/j.cageo.2011.08.017 |
| [11] | Sandwell D, Smith W H F. Retracking ERS-1 Altimeter Waveforms for Optimal Gravity Field Recovery[J]. Geophysical Journal International, 2005,163(1):79-89 |
| [12] | Hwang C, Guo Jinyun, Deng Xiaoli, et al. Coastal Gravity Anomalies from Retracked Geosat GM Altimetry: Improvement, Limitation and the Role of Airborne Gravity Data[J]. Journal of Geodesy, 2006,80(4):204-216 |
| [13] | Garcia E S, Sandwell D T, Smith W H F. Retracking CryoSat-2, Envisat and Jason-1 Radar Altimetry Waveforms for Improved Gravity Field Recovery[J]. Geophys.J. Int.(2014), doi:10.1093/gji/ggt469 |
| [14] | Yang Yuande, E Dongchen, Hwang Cheinwag, et al. Chinese Coastal Gravity Anomalies from Waveform Retracked Geosat/GM Altimetry[J]. Geomatics and Information Science of Wuhan University, 2008,33(12): 1 288-1 291(杨元德,鄂栋臣,黄金维,等. Geosat/GM波形重跟踪反演中国沿海区域重力异常[J]. 武汉大学学报·信息科学版, 2008,33(12):1 288-1 291) |
| [15] | Jin Taoyong, Li Jiancheng, Xing Lelin, et al. Reseach on Datum Unification of Multi-satellite Altimetric Data[J].Journal of Geodesy and Geodynamics, 2008, 28(3):92-95 (金涛勇,李建成,邢乐林,等. 多源卫星测高数据基准的统一研究[J]. 大地测量与地球动力学, 2008, 28(3):92-95) |
| [16] | Olgiati A, Balmino G, Sarrailh M,et al. Gravity Anomalies from Satellite Altimetry: Comparison Between Computation via Geoid Heights and Via Deflections of the Vertical[J]. Bulletin Géodésique,1995,69(4): 252- 260 |
| [17] | Hwang C , Hsu H Y, Jang R J. Global Mean Sea Surface and Marine Gravity Anomaly from Multi-satellite Altimetry: Applications of Deflection-geoid and Inverse Vening Meinesz Formulae[J]. Journal of Geodesy,2002, 76(8):407-418 |
 2015, Vol. 40
2015, Vol. 40


