文章信息
- 周旭华, 王晓慧, 赵罡, 彭海龙, 吴斌
- ZHOU Xuhua, WANG Xiaohui, ZHAO Gang, PENG Hailong, WU Bin
- HY2A卫星的GPS/DORIS/SLR数据精密定轨
- The Precise Orbit Determination for HY2A Satellite Using GPS,DORIS and SLR Data
- 武汉大学学报·信息科学版, 2015, 40(8): 1000-1005
- Geomatics and Information Science of Wuhan University, 2015, 40(8): 1000-1005
- http://dx.doi.org/10.13203/j.whugis20130730
-
文章历史
- 收稿日期: 2013-12-03
2. 国家卫星海洋应用中心, 北京, 100081
2. National Ocean Satellite Application Center, Beijing 100081, China
海洋2A(HY2A)是我国自主研制的一颗海洋动力环境卫星,于2011年8月16日在太原卫星中心发射成功,2012年3月2日正式交付国家海洋局使用。它的发射和应用标志着我国已迈入了海洋环境监测行列。HY2A卫星以实时提供海面高、浪高、海流和海面温度等多种海洋信息为主要目标,提升我国在海洋科学研究,海洋环境监测和预报,全球气候变化等研究中的能力。HY2A卫星设计为太阳同步轨道,倾角99.34 °,寿命为3 a。任务前期采用重复周期为14 d的回归冻结轨道,后期采用重复周期为168 d的回归轨道(www.nsoas.gov.cn)。星载设备有雷达高度计、雷达散射计和微波辐射计以及国产双频GPS接收机,法国DORIS (Doppler Orbitography and Radio-positioning Integrated by Satellite)接收机,SLR(Satellite Laser Ranging)反射棱镜等。
精密轨道的跟踪和确定是HY2A卫星的关键技术,也是有效利用星载设备(如雷达高度计)开展海洋环境监测和研究的前提条件。为满足径向定轨精度优于10 cm的设计要求,HY2A卫星装载了GPS、DORIS和SLR等三种精密跟踪系统,主要由于精密定轨。星载GPS由于其成本低、重量轻、低功耗、全天候、高精度、连续观测等优点,被广泛地安装在精密对地观测的低轨卫星和飞行器上,目前已成为许多低轨卫星精密定轨的主要手段[1, 2, 3, 4, 5]。DORIS 是由法国空间研究中心(CNES)、法国空间测地研究院(CRGS)和国家地理研究院(IGN)联合研制的星基多普勒轨道确定和无线电定位组合系统,该系统主要用于卫星精密定轨和地面精确定位。DORIS具有高精度及全天候等优点,被应用于SPOT-2、TOPEX、Jason-1/2和HY2A等卫星的精密定轨中[6, 7, 8, 9, 10]。SLR单次测距精度己达cm级,逐渐成为卫星精密定轨的重要手段之一[11, 12, 13]。由于SLR观测受天气条件及地面测站分布不均匀等因素的影响,难以实现对空间飞行器的全球、实时跟踪,因此SLR一般作为定轨手段之一,或用于轨道精度检验。
为配合HY2A卫星的科学应用,该卫星的地面应用系统中专门设置了精密定轨分系统,主要负责和协调GPS、SLR、DORIS跟踪站的观测、数据收集、处理及精密轨道确定等工作。当前,HY2A精密定轨分系统中安装了国内4家单位(武汉大学、中科院测量与地球物理研究所、西安卫星测控中心和中科院上海天文台)的精密定轨软件。为实现卫星精密定轨结果的备份和相互检验,4家定轨软件使用的观测资料不完全相同,如上海天文台只用SLR资料进行精密定轨。由于HY2A卫星搭载了DORIS接收机,因此,法国空间研究中心(CNES)每天定时通过FTP向国家卫星海洋应用中心的服务器上传其定轨产品。
随着空间技术的迅速发展,高精度对地观测技术在经济、国防和科研中的地位越来越重要。由于单一数据的定轨模式难以满足高精度、快速、稳定等实际需求,为满足我国航天及相关领域对高精度卫星轨道的迫切需求,需要一种可同时处理多种空间跟踪观测数据的精密定轨软件。为充分发挥GPS、DORIS和SLR三大测量技术的各自优势,本文建立了一套具有对GPS、DORIS和SLR三种数据进行单独和联合(表示为GPS/DORIS/SLR)精密定轨软件,并基于不同数据的先验精度选择适当的权,应用于HY2A卫星的精密定轨中。本文选取HY2A卫星2013年2月的实测数据,以CNES的精密轨道作为参考标准,研究了GPS、DORIS及SLR三种观测手段的单独和联合定轨问题。
1 定轨数据及策略采用的定轨数据、模型及解算参数如下:
1) GPS、DORIS和SLR观测数据:时间跨度为2013-01-31~2013-02-28。GPS数据由国家卫星海洋应用中心提供,采样间隔为1 s。DORIS和SLR数据取自NASA网站。
2) 测站坐标:SLR,SLRF2005;DORIS,DOPOD2005。
3) 地球自转参数:EOP,IERS 08 C04;岁差/章动,IAU2000A。
4) 力学模型:重力场,EIGEN5C模型(150阶×150阶);固体潮摄动,IERS96规范[14];太阳光压摄动,Box-Wing模型[15];海潮摄动,CSR4.0模型[16];N体行星摄动,JPL DE/LE 200大行星历表;广义相对论摄动,IERS2003规范[17];经验RTN摄动;大气阻力摄动,DTM94模型[18]。
5) 对流层延迟改正:SLR,IERS2003;DORIS,Saastamonien+Neil。
6) 估算参数:GPS,每个卫星的每个模糊度弧段解算一个载波相位模糊度和每个历元解算一 接收机钟差;DORIS,每站每圈解算1个频偏参数和对流层折射校正因子;每24 h估算一组初始轨道位置和速度;每24 h估算一次大气阻力参数;经验力参数,每6 h估算一组T、N方向经验力参数(R方向不解);每12 h估算一个太阳光压参数。7) 基于观测数据先验精度,并考虑少量SLR站的测量精度较差的特点,设定的三种观测数据权重为:GPS相位,1 cm;DORIS,0.5 mm/s;SLR,5 cm。
8) CNES的精密轨道由国家卫星海洋应用中心提供。
9) GPS卫星轨道与钟差:采样间隔为15 min的GPS星历和采样间隔为30 s的GPS钟差,上海天文台提供[19]。实际计算中,利用10阶Chebyshev多项式插值GPS星历,利用3阶Lagrange插值GPS钟差。
2 定轨结果及精度分析采用HY2A卫星的GPS、DORIS和SLR观测资料,计算出2013-01-31~2013-02-28的卫星轨道,并通过内符合精度、轨道互比及SLR检验三种手段对定轨结果进行精度评估。
2.1 内符合精度数据残差体现了定轨观测资料的拟合程度,分析定轨观测残差能初步判断定轨参数的解算水平,是定轨精度的一个重要标志。表1给出了2013年1月31日利用GPS/DORIS/SLR资料联合定轨的观测残差统计。
| 数据类型 | 最大值 | 最小值 | 平均值 | 标准差 |
| DORIS/距离变化率/(cm\5s-1) | 0.40 | -0.34 | -0.63×10-6 | 0.048 |
| GPS/相位/cm | 2.09 | -2.08 | 0.15×10-3 | 0.73 |
| SLR/距离/cm | 4.12 | -2.37 | 0.83×10-3 | 2.86 |
从表1中可以看出,三种数据的观测拟合残差符合要求,定轨结果基本可靠。但由于内符精度体现的是观测数据的拟合程度,不能定量地评估卫星轨道的真实精度,因此还不能作为评估定轨结果的绝对手段,必须和其他轨道精度评定方法结合,确保轨道误差分析的可信度。
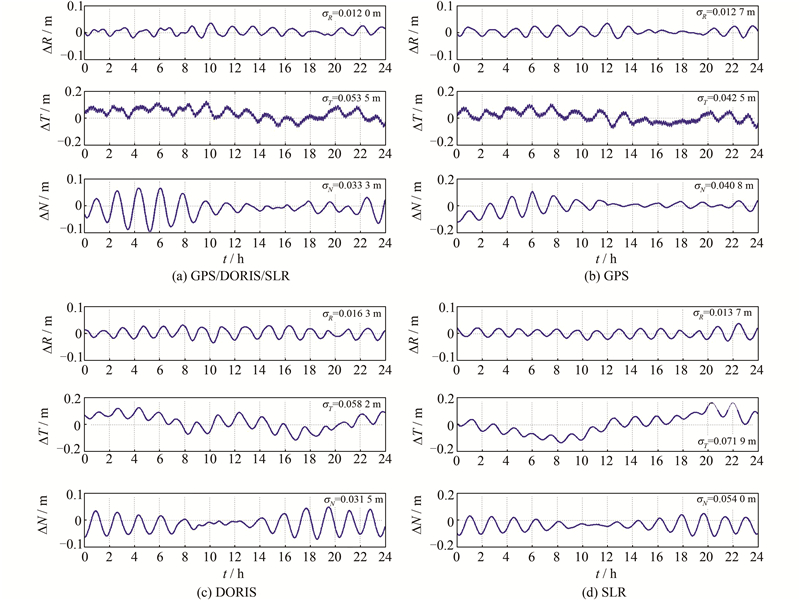
2.2 轨道互比检验根据法国CNES向国家卫星海洋应用中心提供的轨道检测报告,其利用GPS和DORIS数据确定的轨道,两者差异小于5 mm,SLR检验DORIS轨道的径向精度约为2 cm。为此,我们将CNES的轨道作为参考标准来分析定轨精度。图1以2013年1月31日数据为例,并用CNES结果作为标准轨道,定量估计GPS、SLR、DORIS和GPS/DORIS/SLR 4种不同方案的定轨精度。其中R、T、N分别表示径向、切向和法向。由于SLR单天数据少,在用SLR数据单独定轨时,弧长设定为3 d。GPS、DORIS数据的定轨弧长设定为1 d。
|
| 图 1 采用不同资料确定的轨道与CNES结果的比较 Fig. 1 Comparison of CNES Orbits and the Derived Orbits from Different Data |
图1表明,如果把CNES给出的轨道作为标准轨道,那么本文确定2013年1月31日的GPS/DORIS/SLR、GPS、DORIS及SLR 4种不同数据确定的轨道在R方向上的定轨精度分别为 1.20 cm、1.27 cm、1.63 cm和1.37 cm;T方向上的定轨精度分别为5.35 cm、4.25 cm、5.82 cm和7.19 cm;N方向上的定轨精度分别为3.33 cm、4.08 cm、3.15 cm和5.40 cm。三维精度分别为6.4 cm、6.1 cm、6.8 cm、9.1 cm。4种方式计算的卫星轨道径向结果之间差异不大,但从三维位置角度,SLR的定轨结果与CNES结果差别最大。单独采用GPS数据定轨和采用GPS/DORIS/SLR数据联合定轨的差异很小。由于SLR定轨精度取决于观测站对卫星观测弧长、观测站的几何构形等因素,不同时段的SLR定轨结果可能存在较大差异(表2)。特别是对我国一些没有参加国际联测的卫星,如果只依靠中国区域的SLR网,其SLR的定轨结果可能较差。
限于篇幅,其他时段的GPS、SLR、DORIS和GPS/DORIS/SLR定轨结果与图1类似,表2中列出了2013年2月1日~7日的GPS/DORIS/SLR、GPS、DORIS及SLR 4种方案确定的轨道与CNES轨道的差异。
| /cm | ||||||||
| 数据类型 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | |
| GPS/DORIS/SLR | R | 1.11 | 1.36 | 1.30 | 1.19 | 1.22 | 1.27 | 1.26 |
| T | 4.63 | 3.92 | 5.63 | 5.36 | 4.48 | 5.10 | 4.38 | |
| N | 3.26 | 3.7 | 5.17 | 4.92 | 3.64 | 3.73 | 2.83 | |
| 3D | 5.77 | 5.74 | 7.77 | 7.37 | 5.90 | 6.52 | 5.37 | |
| GPS | R | 1.24 | 1.52 | 1.48 | 1.41 | 1.32 | 1.32 | 1.14 |
| T | 3.56 | 3.87 | 5.08 | 4.59 | 5.13 | 5.71 | 4.04 | |
| N | 3.62 | 4.48 | 5.52 | 5.41 | 3.62 | 3.78 | 3.31 | |
| 3D | 5.22 | 6.11 | 7.64 | 7.13 | 6.42 | 6.97 | 5.35 | |
| DORIS | R | 2.04 | 1.42 | 1.74 | 1.44 | 1.71 | 1.86 | 1.51 |
| T | 5.63 | 5.49 | 4.90 | 6.01 | 4.79 | 9.06 | 5.62 | |
| N | 4.49 | 5.01 | 6.57 | 6.93 | 4.66 | 5.80 | 6.52 | |
| 3D | 7.49 | 7.57 | 8.39 | 9.29 | 6.90 | 10.93 | 8.74 | |
| SLR | R | 1.72 | 2.10 | 2.00 | 1.99 | 1.84 | 1.86 | 1.72 |
| T | 5.91 | 7.17 | 9.52 | 5.19 | 11.85 | 8.01 | 8.72 | |
| N | 5.33 | 5.93 | 6.98 | 8.44 | 4.31 | 3.14 | 2.75 | |
| 3D | 8.15 | 9.54 | 11.97 | 10.10 | 12.74 | 8.81 | 9.30 | |
从表2可以看出,联合GPS、DORIS和SLR数据得到的轨道,与CNES精密轨道径向差的平均值为1.26 cm,三维位置差的平均值为6.34 cm,与单独用GPS数据的定轨平均值(径向1.34 cm,三维6.40 cm)非常接近,略好于用DORIS单独数据定轨(径向1.68 cm,三维8.50 cm)。用SLR数据也可以确定出平均值为1.89 cm的径向精度,但由于SLR对径向位置较敏感,对沿迹方向不敏感,所以不同时间段的SLR观测数据量可能差异很大,特别是在观测数据较少时,用SLR数据计算的轨道,其三个方向差异可能较大(如2月5日)。
对精密定轨而言,GPS、SLR和DORIS都可以实现,但卫星的空间环境复杂,在轨设备能否始终保持稳定是一个难题。HY2A卫星装载星载GPS接收机、DORIS系统及SLR反射棱镜,就是为了使三种定轨设备能互为备份和验证,确保卫星科学任务顺利完成。以2013年2月8日数据为例,研究三种数据联合定轨的必要性。具体方法是:(1)直接用GPS数据计算出1 d轨道;(2)假定 GPS只有0~18时的数据,也用这18 h的GPS数据定出1 d轨道;(3)用只有18 h的GPS数据与SLR及DORIS全天数据联合定轨。图2给出了上述三种情况定轨结果与CNES的径向差。

|
| 图 2 定轨结果与CNES的径向差 Fig. 2 Difference Between the Derived Orbits with CNES at Radial Direction |
从图2可以看出,用24 h的GPS数据对HY2A卫星进行精密定轨,其径向与CNES差异为1.24 cm;当GPS数据缩短到18 h时,实际上是前18 h在用GPS数据定轨,后6 h为轨道预报,显然预报结果不如定轨结果;如果利用缺失的GPS数据联合DORIS和SLR数据进行精密定轨,与CNES结果的径向差异为1.36 cm。由于图2的结论具有普遍性,因此可知,多源数据联合定轨能保持计算的轨道精度相对稳定,对科学研究和工程应用都具有重要意义。
2.3 轨道的SLR检验对于星载GPS、DORIS或联合定轨,评估其轨道精度的一个重要手段就是利用高精度的激光测距数据,其依据是SLR单次测距精度优于1 cm。检验结果是SLR直接测得的站星距与定轨结果计算得到的站星距之差。
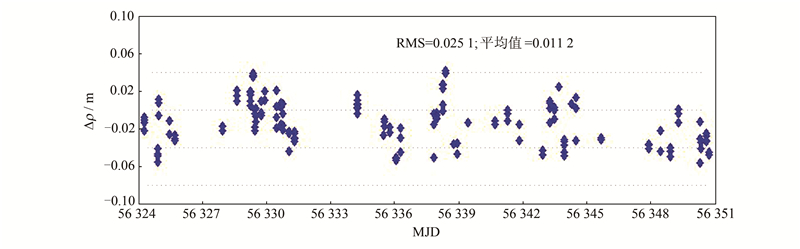
HY2A属于海洋测高卫星,其轨道径向精度是制约雷达高度计数据应用的重要因素。SLR的测量量为测站与卫星的距离,星地距与径向并不重合,只有当卫星接近天顶的情况下,两者才较为接近。为了从轨道误差中分离出径向误差用于SLR检验,本文选择了高度角大于60°的SLR数据。为强调SLR检验的独立性,图3给出了2013年2月由GPS/DORIS两种资料联合定轨结果的SLR检验。
|
| 图 3 SLR检测GPS/DORIS的轨道残差图 Fig. 3 SLR Residuals for GPS/DORIS Orbits |
可以看出,用SLR检验的2013年2月GPS/DORIS两种资料联合定轨结果,在测距方向的残差RMS为2.51 cm,平均值为-1.12 cm。由于HY2A每天的全球SLR观测站和观测量是变化的[13],因此通过站星计算的高度角大于60°的SLR观测数据并不多,可能有些天没有SLR数据参与轨道的检测。评定轨道位置精度角度时,通常使用所有的SLR观测数据,但低高度角往往会导致一些改正项的计算误差较大。假定选择的截止高度角为20°,则此时计算的星地距方向的残差为3.52 cm,比前面选择60°高度角的结果稍大。由于SLR检验卫星轨道时涉及到多项改正,修正后的测距准确值应优于2 cm,检验的站星距结果是可信的。
3 结 语本文基于2013年2月HY2A卫星的实测数据,研究了GPS、DORIS和SLR三种数据的单独和联合定轨精度,结果如下。
1) 由于HY2A卫星加入了国际SLR联测,保证了SLR观测量的相对稳定,也为SLR的高精度定轨提供了数据保证。与CNES的轨道相比,SLR确定的轨道径向与CNES结果差异小于5 cm。HY2A卫星的SLR全球联测及定轨精度对我国后续卫星的精密定轨有借鉴意义。
2) 利用GPS精密星历及钟差,基于非差动力学方法,对HY2A卫星进行精密定轨,结果发现,GPS确定的HY2A卫星轨道与CNES结果在径向上的平均差异约为1.3 cm,三维位置约为6.2 cm。
3) 利用单一的DORIS数据对HY2A卫星进行精度定轨,其结果与CNES轨道的径向差异约为1.6 cm,三维差异好于10 cm,比用单一星载GPS数据的定轨结果稍差。由于本文不是直接用DORIS的RINEX3.0格式数据定轨,而是用距离变化率数据计算,在数据格式转换过程中,可能带来定轨的精度损失,此种情况需要进一步研究。
4) 用GPS、DORIS和SLR三种数据联合定轨,尽管其结果与用GPS单一数据定轨差异很小,在提高定轨精度上效果不明显,但联合定轨能降低定轨过程中参数解算的相关性,有利于保持计算轨道精度的相对稳定,特别是当GPS或DORIS数据出现中断或缺失时,意义明显。
5) SLR 单次测距精度好于1 cm,是检验卫星轨道的重要手段。由于海洋HY2A卫星对轨道径向精度要求较高,因此本文选取了高度角大于60 °的SLR 数据用于轨道检验。对2013年2月SHAO定轨的结果进行检测,发现在测距方向残差的RMS为2.5 cm,满足HY2A卫星 cm级的定轨要求。
| [1] | Kang Z,Tapley B,Bettadpur S, et al. Precise Orbit Determination for GRACE Mission Using only GPS Data[J]. J Geod,2006,80:322-331 |
| [2] | Peng Dongju,Wu Bin. LEO Satellite Using Single-difference and Indifference Method[J]. Chinese Science Bulletin, 2007, 52(6): 715-719 (彭冬菊,吴斌.非差和单差LEO星载GPS精密定轨探讨[J].科学通报,2007,52(6):715-719) |
| [3] | Zhao Q L, Liu J N,Ge M R, et al. Precise Orbits Determination of GPS and CHAMP Satellite with PANDA Software [J]. Joural of Geodesy and Geodynamics, 2005,25(2) :113-116 |
| [4] | Tapley B D, Ries J C, Davis G W,et al. Precise Orbit Determination for TOPEX/Poseidon [J]. Journal of Geophysical Research,1994, 99(C12): 24 383- 24 404 |
| [5] | Guo Qing, Zhao Qile,Li Min, et al. Centimeter Level Orbit Determination for HY2A Using GPS Data [J]. Geomatics and Information Science of Wuhan University,2013,38(1):52-55(郭晴,赵齐乐,李敏,等.利用星载GPS观测数据确定海洋2A卫星cm级精密轨道[J].武汉大学学报·信息科学版,2013,38(1):52-55) |
| [6] | Auriol A,Tourain C.DORIS System:The New Age[J]. Advances in Space Research, 2010,46: 1 484- 1 496 |
| [7] | Willis P, Ries J C. Defining a DORIS Core Network for Jason-1 Precise Orbit Determination Based on ITRF2000:Methods and Realization[J]. Journal of Geodesy, 2005,79:370-378 |
| [8] | Zhao Chunmei, Ou Jikun, Sheng Chuanzhen, et al. JASON-2 Orbit Determination Based on DORIS Data[J]. Progress in Geophysics, 2013, 28(1): 49-57 (赵春梅,欧吉坤,盛传贞,等.基于DORIS数据的JASON-2卫星精密定轨分析[J].地球物理学进展,2013,28(1): 49-57) |
| [9] | Zhu Jun,Wang Jiasong,Chen Jianrong, et al. Centimeter Precise Orbit Determination for HY-2 Via DORIS[J]. Joural of Astronautics, 2013, 34(2): 163-169 (朱俊,王家松,陈建荣,等.HY-2卫星DORIS厘米级精密定轨[J].宇航学报,2013,34(2): 163-169) |
| [10] | Li Peijia, Cao Jianfeng,Hu Xiaogong ,et al.High Accuracy Orbit Determination with DORIS System[J].Journal of Spacecraft TT&C Technology, 2010,29(3):58-64(李培佳,曹建峰,胡小工,等.利用DORIS测轨系统实现高精度定轨[J].飞行器测控学报,2010,29(3):58-64) |
| [11] | Sun Mingguo, Liu Chengzhi, Fan Cunbo, et al. Analysis on the Accuracy of Celestial Positioning Based on the SLR Precise Orbit[J]. Acta Astronomica Sinica, 2012,53(2):153-160(孙明国,刘承志,范存波,等.基于SLR精密轨道的天文定位精度分析[J].天文学报,2012,53(2):153-160) |
| [12] | Qin Xianping, Yang Yuanxi, Jiao Wenhai,et al. Combined Determination of Satellite Orbit Using SLR and Pseudorange Data[J]. Geomatics and Information Science of Wuhan University, 2003,28(6):745-748(秦显平,杨元喜,焦文海,等.利用SLR与伪距资料综合定轨[J].武汉大学学报·信息科学版, 2003,28(6):745-748) |
| [13] | Zhao Gang, Zhou Xuhua, Wu Bin. Precise Orbit Determination for HY-2 Satellite Using SLR Data[J]. Chinese Science Bulletin, 2012, 57 (36): 3 475-3 483(赵罡,周旭华,吴斌. 海洋二号卫星SLR精密定轨[J].科学通报,2012,57 (36): 3 475-3 483) |
| [14] | McCarthy D D. Effect of Solid Earth Tides[Z]. IERS Technical Note, 1996, 21: 40-46 |
| [15] | Rim H J. TOPEX Orbit Determination Using GPS Tracking System[D]. Austin: University of Texas at Austin, 1992 |
| [16] | Eanes R, Schuler A. An Improved Global Ocean Tide Model from TOPEX/POSEIDON Altimetry : CSR4.0[C]. EGS 24th General Assembly, Hague, Netherlands, 1999 |
| [17] | McCarthy D D, Petit G. Equations of Motion for an Artificial Earth Satellite[Z]. IERS Technical Note, 2003, 32:106-107. |
| [18] | Berger C, Biancale R, Ill M, et al. Improvement of the Empirical Thermospheric Model DTM: DTM94 -A Comparative Review of Various Temporal Variations and Prospects in Space Geodesy Applications[J]. J Geod, 1998,72: 161-178 |
| [19] | Chen J P,Zhang Y Z, Zhou H, et al. GNSS Clock Corrections Densification at SHAO: from 5 min to 30 s[J]. Sci Sin Phys Mech Astron, 2013 ,56(2):1-10 |
 2015, Vol. 40
2015, Vol. 40


