文章信息
- 张黎明, 闫浩文, 齐建勋, 张永忠
- ZHANG Liming, YAN Haowen, QI Jianxun, ZHANG Yongzhong
- 基于DFT的可控误差矢量空间数据盲水印算法
- A Blind Watermarking Algorithm for Copyright Protection of Vector Geospatial Data Under Controllable Errors Based on DFT
- 武汉大学学报·信息科学版, 2015, 40(7): 990-994
- Geomatics and Information Science of Wuhan University, 2015, 40(7): 990-994
- http://dx.doi.org/10.13203/j.whugis20130686
-
文章历史
- 收稿日期:2013-11-15
2. 甘肃省地理国情监测工程实验室, 甘肃 兰州, 730070;
3. 兰州市勘察测绘研究院, 甘肃 兰州, 730000
2. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China;
3. Lanzhou City Survey Mapping Institute, Lanzhou 750050, China
地理信息系统(GIS)与计算机网络技术的飞速发展,一方面为各种数字化地图产品的存取、拷贝和传播提供了极大的方便;但另一方面,使得盗版变得极其容易[1]。因此,如何进行空间数据的版权保护,引起了地学界的高度重视。目前,常用数字水印技术来保护数字地图版权[2]。
数字水印具有两个重要特征:不可见性与鲁棒性[1]。不可见性要求水印嵌入空间数据后引起的误差要尽可能小,由此导致的空间位置误差不易为用户感知;鲁棒性是指带水印的空间数据在几何变换、数据编辑、数据格式转换等操作中水印信息能够保持完整。一般来说,变换域算法比空间域算法鲁棒性高,这也是目前水印算法研究的主要方向[3]。
本文将提出一个基于离散傅里叶变换(discrete Fourier transform,DFT)的盲水印算法。
1 DFT变换域水印算法的原理矢量空间数据在使用中通常会进行几何变换,而DFT对几何图形平移、旋转、缩放等具有不变性特点,所以基于DFT的水印算法在抗几何攻击上具有天然的优势[9]。文献[4, 5, 6, 7, 8, 9, 10, 11, 12, 13]都是基于DFT的数字水印算法,这类算法的原理是:选择图形的坐标点 vk,得到顶点序列{vk}(vk=(xk,yk))。根据表达式(1),将xk和yk组合起来表示成一个复数序列{ak}:

式中,N为图形顶点数目。
对{ak}做DFT变换,根据式(2)得到离散傅里叶系数{Al}:
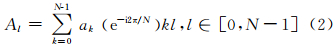
{Al}包含了幅度系数{|Al|}和相位系数{∠Al}。 通过使用不同的水印嵌入方法,水印可以嵌入到DFT变换后的幅度系数上,也可以嵌入到相位系数中。但是,水印直接嵌入变换后的系数中,会对原始数据产生较大影响,特别是相位系数的较小改变可能导致原始数据的较大改变。
文献[9]通过加法法则把水印信息嵌入DFT变换后的相位系数,对提取出的水印信息与原始水印信息进行对比,根据自相关检测系数判定是否含有水印信息。实验选择嵌入强度P=0.02~0.03,嵌入水印后,最大误差达到两个单位的坐标点有1 883个。
文献[10]通过量化方法把水印信息嵌入变换后的幅度系数中。实验选取的量化步长是50、100、200。量化步长为50时,最大误差达到两个单位,随着量化步长的增大,最大误差甚至超过了3个单位。这是因为该算法将水印直接嵌入DFT变换后的幅度系数中,对原始数据产生了较大影响,引起了较大的误差。此外,DFT变换后,幅度系数与原始数据的数值大小有关,幅度系数越小,直接量化嵌入幅度系数引起的坐标误差越大。
本文利用DFT变换的自身特点,设计了一种可控误差的矢量空间数据盲水印算法。该算法既能保证变换域水印的鲁棒性,又使得水印嵌入引起原始数据的误差较小,且实现盲检测。
2 水印嵌入与提取算法在DFT水印算法中,水印信息既可嵌入变换后的幅度系数,也可以嵌入变换后的相位系数。DFT变换后,幅度系数具有平移和旋转不变性,相位系数具有平移和缩放不变性。因此,在幅度系数中嵌入水印,可以抵抗几何变换中的平移和旋转操作对水印的影响;在相位系数中嵌入水印,可以抵抗几何变换中的平移和缩放操作对水印的影响。为了能在几何变换操作中保证水印不受影响,本算法将水印独立嵌入幅度系数和相位系数中,可以同时从幅度系数和相位系数中提取水印。
由于DFT本身就是一种浮点运算,不管是浮点型的矢量空间数据还是整数型的矢量空间数据,通过DFT变换后,幅度系数和相位系数都会以浮点数表示。DFT变换中,浮点数采用Double类型的数据,Double类型的数据有效位数为15~16位。为了满足不同矢量空间数据水印嵌入的需要,水印信息应合理嵌入到变换后系数的有效数据位部分。权衡水印的鲁棒性和数据的精度要求,一般选择Double类型的数据小数位的8~10位嵌入水印。
为了实现盲水印,本算法采用区间量化方法嵌入水印。具体实现步骤是,对变换后的系数,放大10n倍。根据DFT变换系数的大小并顾及数据的精度要求,自适应计算出n的大小,从而控制了水印嵌入引起的误差范围。水印信息通过调整系数的量化区间,嵌入到放大后的幅度系数和相位系数中。由于系数是以浮点数存储,系数的放大只是改变了指数值的大小,对底数(有效数据)不会有影响,因此不会产生截断误差。同样,系数缩小后也不会产生误差。
由于傅里叶变换是一种全局变换,局部很小的修改就可以引起全部傅里叶系数的变化,导致水印算法对于局部修改没有鲁棒性[14]。为了克服小范围的修改不至于引起全部傅里叶系数的变化,本算法把二维矢量地图基本图形对象作为一个独立的嵌入单位,个别图形对象的删除、修改操作不会影响其他图形对象中嵌入的水印信息。
为了能完整地提取水印,矢量地理空间数据的坐标点数应不少于水印的比特数。当坐标点数较多时,水印可能被多次嵌入;提取水印时,采用投票原则,以使提取到的水印更加可靠。
2.1 水印嵌入算法水印的生成与嵌入具体过程如下:
1) 水印的生成:读取原始二值水印图像,应用Logistic混沌变换[15]来置乱水印图像;然后变换置乱后的水印图像为一维序列 {wi=0,1|i=0,1,…,M-1},M为水印长度。
2) 读取矢量地理空间数据,以几何对象(线对象或面对象)为单位进行水印信息的嵌入。读取几何对象的所有顶点坐标,根据式(1)产生复数序列{ak}。
3) 对{ak}进行DFT变换,由式(2)得到变换后的DFT系数{al}。该序列包括幅度系数{|Al|}和相位系数{∠Al}。
4)对{|Al|}和{∠Al}分别放大10n倍。
幅度系数放大的倍数需要考虑幅度的数量级。假定量化值R=20。如果直接嵌入幅度系数,水印嵌入引起的最大误差为R/2;而通过放大系数10n后,嵌入水印引起的误差就是原来的1/10n。n的计算方法如下:假如要求水印嵌入到幅度系数的第9~10有效数据位,可以通过n=9-lg(|Al|)来计算n的大小。而相位系数一般介于-π~π,n取7~11为宜。幅度系数和相位系数放大的倍数n不一定相同。
根据量化嵌入法则,将放大后的幅度系数{|Al|}和相位系数{∠Al}嵌入水印数据。通过式(3)计算得出嵌入水印后的系数A′ l:
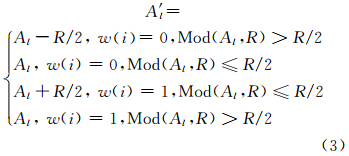
其中,R为量化值。
根据嵌入的水印是“0”还是“1”,将量化区间调整到所在区间或保持不变。如嵌入水印为“0”,原来量化值大于R/2,则需调整量化区间到[0,R/ 2 ,具体计算方法为系数值减去R/2。
6) 将嵌入水印后的傅里叶系数再缩小到原来的大小。
7) 对{ A′ l 进行离散傅里叶逆变换,得到嵌入水印后的复数序列{a′ k}。
根据{a′ k}修改顶点坐标,得到嵌入水印后的矢量数据。
2.2 水印提取算法水印提取是水印嵌入的逆过程。具体如下:
1) 读取待测数据,根据式(1)产生复数序列{a′ k}。
2) 对{a′ k}进行DFT变换,得到离散傅里叶系数{ A′ l 。
3) 对{ A′ l 幅度系数和相位系数分别放大10n倍。
采用嵌入水印时的量化值R,计算出系数所在的量化区间,各自提取出幅度系数水印和相位系数水印。
对提取到的两个一维水印序列,进行升维处理并反置乱,得到最终水印图像。
由于每一个水印位{wi}可能被多次嵌入,因此采用投票原则来确定水印信息。计算方法是:定义一个与水印序列等长的整数序列{B(i)=0,i=0,1,…,M-1},M为水印长度。单个水印位b′ i 通过式(4)量化提取计算:
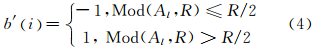
相同水印位提取过程中,使用公式B(i)=B(i)+ b′(i)来统计出水印信息值-1和1的多数,如“1”为多数,则B(i)>0;然后根据式(5)来重构出二值水印图像:
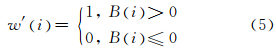
为了检验算法在不同矢量空间数据下的普适性,本文用一幅1∶5 000境界线地图和一幅1∶400万的全国地形图进行试验。数据格式为ArcGIS的shp格式。前者要素层数据量约为349 KB,共有20 292个坐标点;后者要素层数据量约为1.33 MB,共有80 965个坐标点。实验中,水印嵌入到点坐标数值有效位的9~10位。对两组数据嵌入水印后的误差进行了统计,并从嵌入水印后数据的可用性、不可见性、鲁棒性及误差控制等几个方面进行了分析。实验中用的水印是64像素×64像素的二值水印图像,如图 1所示。

|
| 图 1 原始水印 Fig. 1 Original Watermark |
本文采用绝对误差和最大误差来统计评价数据精度,结果如表 1所示。
| R | 4 | 20 | 50 | 100 |
| 1:5000 |  |  |  | 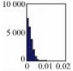 |
| 最大误差 | 0.000 336 | 0.001 8 | 0.004 6 | 0.010 2 |
| 1:400万 |  |  | 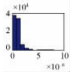 | 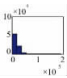 |
| 最大误差 | 1.0×10-6 | 4.0×10-6 | 8.0×10-6 | 1.9×10-6 |
从表 1可以看出,嵌入水印所引起的坐标数据绝对误差均很小。随着量化值R的增加,误差逐步增加,最大误差也逐渐增加。因此,从绝对误差的分布及最大误差数值可以看出,该算法对数据精度影响较小。
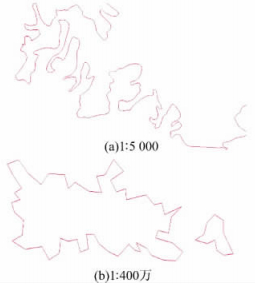
3.2 不可见性试验中,取量化步长R分别为4、20、50、100,在1∶5 000和1∶400万两组不同比例尺数据下,嵌入水印前后局部放大效果如图 2所示。虽然嵌 入水印前后图形分别用不同颜色表示,但是,从 图 2可以看出,嵌入水印前后图形几乎完全重合。此外,从数据绝对误差分析可以看出,嵌入水印后,最大误差远远小于1个单位。用合理的系数放大后,水印会嵌入有效数据的中部。在这个范围内,量化步长对水印的可见性几乎没有影响。
|
| 图 2 嵌入水印前后比较 Fig. 2 Comparison of Original Data and Watermarked Data |
量化值R取20。通过对1∶5 000含水印数据在无攻击、数据格式转换、平移、缩放、删除图形对象等情形下进行仿真实验,均能够很好地提取水印图像(表 2)。对1∶400万数据也进行同样的攻击试验,效果良好。在数据格式转换时,将嵌入水印的数据转换为MapInfo格式数据,再逆转为原格式数据,同样能够很好地提取水印信息。
试验中,在50%的图形对象中仍然能够提取水印。这是因为在水印嵌入时,以图形对象为单位分别独立、多次嵌入,因此,删除部分图形对象后,从剩余图形对象中仍然能够提取到水印。
如果对图形对象内部随机删点后,则几乎无法提取到水印。这是由于DFT变换的局部性,使得增加、删除点后,傅里叶变换系数会发生很大的变化,水印遭到破坏。
此外,R取4、10、20、50、100、200,作了如表 2同样的试验,效果同样较好。当R<4或R>200时,在无攻击的情形下,提取到的水印效果不好;如果R太小,量化提取区间不明显;R较大,系数修改较大,提取时水印效果较差。
3.4 误差控制以1∶5 000数据为例,取R=20,相位系数放大倍数为1010保持不变情况下,分别以不同的放大倍数(表 3)进行试验。从表 3可以看出,在合理的放大倍数下,均可以很好地提取到水印信息,并且能够控制最大误差。
| 放大系数 | 103 | 106 | 109 |
| 提取水印 |  |  |  |
| 最大误差 | 0.007 9 | 7.000 0 | 7.000 0 |
本文针对DFT变换的特点,提出了基于DFT的可控误差矢量空间数据盲水印算法。算法简单,易于实现,可适用于不同比例尺矢量数据水印嵌入。但是由于不同比例尺数据所允许的误差不同,所以在确保数据精度的同时,为了提高水印的鲁棒性,尽可能将水印嵌入到较高的有效数据位部分。通过仿真试验,可以看出算法具有很好的可用性、不可见性,同时对几何变换具有很好的鲁棒性,是矢量空间数据版权保护的一种实用方法,该方法已应用于大比例尺空间数据水印系统中,使用效果良好。
| [1] | Yan Haowen, Li Jun, Wen Hong. A Key Points-Based Blind Watermarking Approach for Vector Geo-Spatial Data[J]. Computers, Environment and Urban Systems, 2011, 35(6):485-492 |
| [2] | Niu Xiamu, Shao Chengyong, Wang Xiaotong. A Survey of Digital Vector Map Watermarking[J]. International Journal of Innovative Computing, Information and Control,2006,2(6):1 301-1 316 |
| [3] | Kang H I I, Kim K I I, Choi J U K. A Vector Watermarking Using the Generalized Square Mask[C]. Information Technology:Coding and Computing, Proceedings of International Conference on IEEE, San Jose, California, USA,2001 |
| [4] | Lee S H, Kwon K R. Vector Watermarking Scheme for GIS Vector Map Management[J]. Multimedia Tools and Applications,2013,doi:10.1007/s11042-011-0894-y |
| [5] | Solachidis V, Nikolaidis N, Pitas I. Fourier Descriptors Watermarking of Vector Graphics Images[C].Proceedings of 2000 International Conference on IEEE (Image Processing), Vancouver B C, Canada, 2000 |
| [6] | Solachidis V, Pitas I. Watermarking Polygonal Lines Using Fourier Descriptors[J]. Computer Graphics and Applications, IEEE, 2004, 24(3):44-51 |
| [7] | Giannoula A, Nikolaidis N, Pitas I. Watermarking of Sets of Polygonal Lines Using Fusion Techniques[C].Multimedia and Expo, ICME'02, Lausanne, Switzerland,2002 |
| [8] | Kitamura I, Kanai S, Kishinami T. Copyright Protection of Vector Map Using Digital Watermarking Method Based on Discrete Fourier Transform[C]. Geoscience and Remote Sensing Symposium, IGARSS'01, Sydney,2001 |
| [9] | Wang Qisheng,Zhu Changqing,Xu Dehe.Watermarking Algorithm for Vector Geo-spatial Data Based on DFT Phase[J]. Geomatics and Information Science of Wuhan University,2011,36(5):523-526(王奇胜,朱长青,许德合.利用DFT相位的矢量地理空间数据水印方法[J].武汉大学学报·信息科学版,2011,36(5):523-526) |
| [10] | Xu Dehe,Zhu Changqing, Wang Qisheng.Blind Watermarking Model of Vector Spatial Data Based on DFT of QIM[J]. Geomatics and Information Science of Wuhan University, 2010,35(9):1 100-1 103(许德合,朱长青,王奇胜.利用QIM的DFT矢量空间数据盲水印模型[J].武汉大学学报·信息科学版,2010,35(9):1 100-1 103) |
| [11] | WANG Qisheng. Research on Digital Watermarking for Vector Geo-spatial Data Based on DFT[D]. Zhengzhou:Information Engineering University, 2008 (王奇胜.基于DFT的矢量地理空间数据数字水印技术研究[D].郑州:信息工程大学,2008) |
| [12] | Xu Dehe. Research on the Model of the Digital Watermarking for Vector Geo-spatial Data Based on DFT[D]. Zhengzhou:Information Engineering University,2008 (许德合.基于DFT的矢量地理空间数据数字水印模型研究[D]. 郑州:信息工程大学,2008) |
| [13] | Zhao Lin. Research on Adaptive Vector Map Watermarking Algorithm Based on DFT[D]. Harbin:Harbin Engineering University,2009 (赵林. 基于DFT自适应矢量地图水印算法的研究[D]. 哈尔滨:哈尔滨工程大学,2009) |
| [14] | Min Lianquan. A Survey of Watermarking Techniques for Vector Map Data[J]. Journal of Geomatics Science and Technology, 2009(2):96-102(闵连权. 矢量地图数据的水印技术综述[J]. 测绘科学技术学报, 2009(2):96-102) |
| [15] | Pareek N K, Patidar V, Sud K K. Image Encryption Using Chaotic Logistic Map[J]. Image and Vision Computing, 2006,24(9):926-934 |
 2015, Vol. 40
2015, Vol. 40









