文章信息
- 徐丰, 牛继强, 李卓凡
- XU Feng, NIU Jiqiang, LI Zhuofan
- 基于粗集的多粒度空间方向关系不确定性定量评价模型
- Quantitative Evaluation Model of the Uncertainty of Multi-granularity Space Direction Relations Based on Rough-Set
- 武汉大学学报·信息科学版, 2015, 40(7): 971-976
- Geomatics and Information Science of Wuhan University, 2015, 40(7): 971-976
- http://dx.doi.org/10.13203/j.whugis20130126
-
文章历史
- 收稿日期:2013-05-13
空间方向关系是GIS的重要理论问题,在地理信息系统的空间数据建模、空间查询、空间分析、空间推理、制图综合、地图解译等过程中起着十分重要的作用。目前较为典型的空间方向关系描述模型主要有锥形模型、最小外切矩形模型、Freksa-Zimmerman模型、2D-String模型、空间方向关系矩阵模型、方向Voronoi图模型[1, 2, 3, 4, 5]等,近年来也出现了运用模糊集、粗糙集和概率论等进行方向关系的近似描述的研究[6, 7, 8, 9, 10]。客观世界中,除了确定性地理目标,还存在许多的不确定性地理目标[11]。于是,不确定性地理目标间方向关系的建模得到了广泛关注,国内外学者已建立了若干不确定方向关系的表示方法[12, 13, 14, 15, 16],成为空间数据不确定性的重要研究内容。总体来说,空间方向关系的不确定性主要来源于以下两个方面:① 地理目标自身的不确定性或其空间位置数据的不确定性;② 方向关系模型及方向系统划分的粒度。前者的研究较多,也取得了比较多的研究成果[17, 18],而对后者的研究相对较少,且主要是对不确定方向关系的定性描述。
由于不确定性地理目标与确定性地理目标引起方向关系不确定性的原因不同,本文将粗集理论用于不确定方向关系的统一表达,重点对确定性地理目标位置不确定性及方向系统划分粒度引起的不确定方向关系进行研究并构建基于知识(方向系统划分粒度)含量的近似精度与粗糙度作为度量空间方向关系不确定性的标量。用于确定性地理目标位置不确定性及方向系统划分粒度引起的方向关系不确定性的定量评价,为空间推理与空间查询等应用的可靠性提供依据。
1 空间方向关系的粗集表达在确定性地理空间中,参考目标、源目标和参照系统是描述空间方向关系的三要素。锥形模型在表示简单的空间对象间的空间方向关系时有其独有的优势,因此,在GIS中得到了广泛的应用,目前仍是空间方向关系的主要描述模型[8]。粗集在揭示和表达多层次或多粒度的空间知识方面具有较大的优势,不仅可以定性描述不确定性问题,而且还可以用于定量评价不确定性程度。本文基于锥形模型建立空间方向关系的粗集表达。
1.1 空间方向关系描述锥形模型从空间参考点出发将其周围的区域划分成若干具有方向性的子区域,并根据源目标与这些子区域相交的情况来确定源目标与其空间参考目标(点)之间的方向关系,常用的方向划分粒度为4方向、8方向、16方向,甚至粒度划分更细,如图 1。如果源目标落在某一方向的锥形区域内,则认为源目标在参考目标的该主方向上。

|
| 图 1 空间方向关系锥形模型 Fig. 1 Cone-shaped Models of Spatial Direction Relations |
在该模型中,方向参考系统的中心是一个点,当参考目标为点时,该点就是方向参考系统的中心;当参考目标为线或面时,方向参考系统的中心较难确定,本文以线或面的质心为方向参考系统的中心。因为锥形模型中参考点的位置是最难确定的,对锥形模型参考点位置不确定的缺陷,现有研究大多通过对锥形模型的改进来弥补,故本文不考虑参考点的位置不确定性问题。
1.2 源目标的粗集表达在GIS中,将确定性地理目标分为点目标、线目标、面目标。已有确定性地理目标位置不确定性的粗集表达中,目标边界的不确定性[19]即为粗集的边界[17]。将源目标的粗集表达进一步用于定义不确定方向关系,应首先确定源目标在锥形模型中方向分布范围的边界。
1.2.1 点目标的粗集表达当源目标PO为点时,若其点位误差为ε,则PO的粗集表达(图 2(a))为:


|
| 图 2 锥形模型中点、面目标位置不确定性的粗集表达 Fig. 2 Rough-set Representation of Positional Uncertainty on Point Object and Area Object in Cone-shaped Model |
式中,·表示目标形态膨胀算子,PO 、PO 和 Bn(PO)分别表示源目标粗集表达的下近似、上近似和边界。
1.2.2 线目标的粗集表达当源目标PO为线时(由节点P1、P2、…、Pn及其连线构成),首先寻找折线在锥形模型中方向分布的边界点,边界点为以参考点为视点的线目标的可视部分的外边界点[2]。边界点的寻找过程为:以参考目标(点)为坐标原点,任一从坐标原点发出的与线目标不相交的射线方向为极轴建立极坐标系,线目标PO上节点Pi(i=1,2,…,n)的极坐标为Pi(αi,ρi),计算αmax=max(α1,α2,…,αn),αmin=min(α1,α2,…,αn),在线目标PO上节点中查找其极角与αmax相等的节点PS和与αmin相等的节点PE,若PS和PE不止一个,分别取其中极径最小的节点为PS和PE,然后在线目标上截取以PS和PE为端点的折线段即为PO′。只有PS和PE两点的位置不确定性会引起线目标方向关系的不确定性。例如图 3>(a)P2和P5两点的位置不确定性会引起线目标方向关系的不确定性,是定义线方向分布范围的边界点。

|
| 图 3 锥形模型中折线方向及其粗集表达 Fig. 3 Direction Relations of Polygonal Line and Its Rough-set Representation in Cone-shaped Model |
文献[15]中地理目标的粗集表达是从地理目标位置不确定性的角度去描述的,它所定义的线目标的下近似改变了线目标沿某一方向延展的特性,不适用于进一步定义方向关系的粗集表达。因此,若线目标PO误差带的宽度为2ε,则线PO的粗集表达(图 3(b))为:
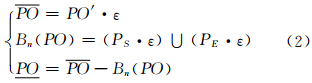
式(2)对于线段同样适用。式(2)定义的线目标的粗集表达对于进一步推导其不确定方向关系有意义,但不能用于描述线目标的位置不确定性。
1.2.3 面目标的粗集表达当源目标PO为面时,若其面位误差环的宽度为2ε,则面PO的粗集表达(图 2(b))为:
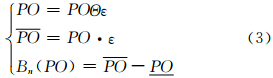
式中,Θ表示目标形态侵蚀算子。
1.3 空间方向关系的粗集表达锥形模型所分解的平面空间即为粗集中的论域空间,具体方向的划分方法即为粗集论域集合上的划分函数,锥形模型所划分的各主方向即为粗集知识(库)。因此,方向关系锥形模型的粗集描述如定义1。
定义1 假设论域空间 U为以O为圆心的圆形区域(360°),R是U上的一族基于方向划分的等价关系,令K=(U,R)为方向关系知识库,U/R={O1,O2,…,On},On (n=4,8,16,…)为基于锥形模型以O为参考点对U划分的n个方向区域,当n=4时,U/R={N,E,S,W},方向关系知识库中每个元素对应的圆心角为90°;当n=8时,U/R={N,NE,E,SE,S,SW,W,NW},方向关系知识库中每个元素对应的角度为45°等。
据此可以定义源目标PO隶属于锥形模型基于参考点O所划分的n(n为方向分辨率,n=4,8,16,…)个方向区域Oi(1≤i≤n)的隶属函数为:
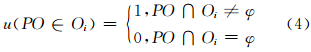
式中,u为隶属函数。
参考目标O和源目标PO间的方向关系为:
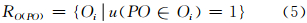
定义2 源目标PO相对于参考目标(点)O的方向关系RO(PO)的下粗近似集为 R O(PO),上粗近似集为RO(PO),RO(PO)=RO(PO) ={Oi|u(PO ∈Oi)=1},RO(PO)=RO(PO) ={Oi u(PO ∈Oi)=1 },RO(PO)的边界集合BN(RO(PO))= O(PO)-RO(PO)。
具体计算中,先确定方向分辨率n,再结合定义2利用式(4)、式(5)确定空间目标不确定方向关系的粗集表达结果。
2 空间方向关系不确定性度量粗集不确定性的来源主要有系统不确定性和概念不确定性[20]。在空间方向关系的粗集表达中,空间数据位置不确定性引起的方向关系粗集表达的不确定性属于系统不确定性;方向系统划分粒度引起的空间方向关系的不确定性属于概念不确定性。定性描述概念不确定性是GIS中的一种重要方式,但在实际应用中计算机处理存在一定的问题。本文采用概念不确定性的定量描述,在实际应用中可以再根据具体需要转换成定性描述。本文提出基于粗集的多粒度空间方向关系不确定性定量指标主要包括:① 近似精度与粗糙度,用于度量空间数据位置不确定性引起的方向关系粗集表达的不确定性;② 知识含量,用于度量锥形模型粗集表达的方向分类能力;③ 基于知识含量的近似精度与粗糙度,用于确定性地理目标位置不确定性及方向系统划分粒度引起的方向关系不确定性的定量评价。
2.1 近似精度与粗糙度定义3 称
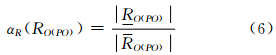
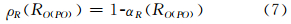
分别为空间对象PO相对于参考点O的方向关系集合RO(PO)的近似精度和粗糙度。
其中,αR(RO(PO))为近似精度,ρR(RO(PO))为粗糙度,丨RO(PO) 丨表示方向关系上粗近似集 O(PO)中元素的个数,丨RO(PO) 丨表示方向关系下粗近似集RO(PO)中元素的个数。
αR(RO(PO))和ρR(RO(PO))可以用来度量空间数据位置不确定性引起的方向关系粗集表达的不确定性。αR(RO(PO))和ρR(RO(PO))都是一个区间[0, 1]上的实数,αR(RO(PO))越大,集合RO(PO)的确定度就越大;ρR(RO(PO))越大,集合RO(PO)的不确定度就越大。
2.2 知识含量的度量方向关系的粗集表达中,方向系统划分的粒度即为粗集中知识的粒度。知识R含量的测度用于度量锥形模型粗集表达的方向分类能力。本文中的知识均指方向系统划分产生的主方向。
定义4 对于基于锥形模型的方向关系知识库K=(U,R),U/R={O1,O2,…,On},称
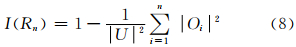
为知识R含量的测度。其中,I(Rn)为知识R含量的测度。
根据式(8)方向系统划分粒度n与知识R含量的测度I(Rn)的对应关系见表 1。
| n | 4 | 8 | 16 | 32 | 64 | … | 360 |
| |Oi| | 90 | 45 | 22.5 | 11.25 | 5.625 | … | 1 |
| I(Rn) | 0.75 | 0.875 | 0.938 | 0.969 | 0.984 | … | 0.997 |
通过表 1可以看出,I(Rn)随方向系统划分粒度n的增大而增大,这与“n越大,方向划分越准确”是一致的。
2.3 基于知识含量的近似精度与粗糙度基于知识含量的近似精度和粗糙度是在近似精度和粗糙度中引入知识含量的测度因子I(Rn),克服了近似精度和粗糙度不能全面衡量粗集不确定性的缺点。
定义5 空间对象PO相对于参考点O的方向关系为RO(PO),称
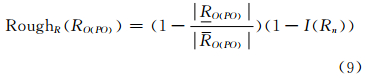

分别为RO(PO)关于U上的等价关系R的基于知识(方向系统划分粒度)R含量的粗糙度和近似精度。
其中,丨RO(PO) 丨表示方向关系上粗近似集 RO(PO)中元素的个数;O(PO) 表示方向关系下粗近似集 RO(PO)中元素的个数。
RoughR(RO(PO))和DR(RO(PO))都是一个区间[0, 1]上的实数,空间方向关系系统划分粒度越小,I(R)越大,DR(RO(PO))越大,RoughR(RO(PO))越小,集合RO(PO)的确定度就越大,不确定度就越小,反之亦然。RoughR(RO(PO))和DR(RO(PO))用于综合评价由于粗集边界(位置不确定性引起)和方向系统划分粒度引起的方向关系的不确定性。
3 实例与讨论根据本文提出基于粗集的多粒度空间方向关系不确定性定量评价模型,选择具有代表性的实验数据对其进行评价。实验数据见图 4,其中参考点位置为参考目标的质心,源目标为目标1(点目标)、目标2(线目标)、目标3(面目标)。实验中首先对图 4中目标1、目标2、目标3按其精度指标计算其粗集表达结果(表 2),然后计算方向关系的不确定性评价的指标:近似精度,粗糙度,基于知识含量的近似精度,基于知识含量的粗糙度(表 3),对源目标的不确定性进行评价。经分析得到如下结论。

|
| 图 4 实验数据 Fig. 4 The Experimental Data |
| 上近似 | 下近似 | 边界集合 | ||
源目 标1 | 方位角 … 16方向系统 8方向系统 4方向系统 | [253°,264°] … {W,WSW} {W} {W} | Φ … Φ Φ Φ | [253°,264°] … {W,WSW} {W} {W} |
| 源目 标2 | 方位角 … 16方向系统 8方向系统 4方向系统 | [305°,353°] … {NW,NNW,N} {NW,N} {W,N} | [312°,345°] … {NW,NNW} {NW,N} {W,N} | [305°,353°]∪ [312°,345°] … {N} Φ Φ |
| 源目 标3 | 方位角 … 16方向系统 8方向系统 4方向系统 | [47°,90°] … {NE,ENE,E} {NE,E} {E} | [64°,78°] … {ENE} {NE,E} {E} | [47°,78°]∪ [64°,90°] … {NE,E} Φ Φ |
1) 近似精度和粗糙度只能部分反映粗集的不确定性。随着方向系统划分粒度的增大,近似精度和粗糙度的变化规律不明显,与人类空间认知逻辑不一致(表 3),因此,近似精度和粗糙度只能部分反映粗集的不确定性。
| 近似 精度 | 粗糙 度 | 基于知识 含量的近 似精度 | 基于知识 含量的 粗糙度 | ||
| 源目 标1 | 方位角 … 64方向系统 32方向系统 16方向系统 8方向系统 4方向系统 | 0 … 0 0 0 0 0 | 1 … 1 1 1 1 1 | 0.997 … 0.984 0.969 0.938 0.875 0.75 | 0.003 … 0.016 0.031 0.062 0.125 0.25 |
| 源目 标2 | 方位角 … 64方向系统 32方向系统 16方向系统 8方向系统 4方向系统 | 0.688 … 0.7 0.8 0.667 1 1 | 0.312 … 0.3 0.2 0.333 0 0 | 0.999 … 0.995 0.994 0.98 1 1 | 0.001 … 0.005 0.006 0.02 0 0 |
| 源目 标3 | 方位角 … 64方向系统 32方向系统 16方向系统 8方向系统 4方向系统 | 0.326 … 0.444 0.4 0.333 1 1 | 0.674 … 0.556 0.6 0.667 0 0 | 0.998 … 0.991 0.981 0.96 1 1 | 0.002 … 0.009 0.019 0.04 0 0 |
2) 基于知识含量的近似精度和粗糙度是较为理想的指标。基于知识含量的近似精度随方向系统划分粒度的增大而减小,基于知识含量的粗糙度随方向系统划分粒度的增大而增大(表 3),说明基于知识含量的近似精度和粗糙度对方向系统划分粒度的变化是敏感的,是评价由于目标位置不确定性及方向系统划分粒度引起的方向关系不确定性的理想指标。
3) 部分源目标不符合变化规律。本实验中线目标和面目标不确定边界方向分布范围比4方向系统和8方向系统主方向范围小很多,使得线及面目标方向关系在4方向及8方向系统中的粗集表达的上近似和下近似相等,从而导致表 3中标有下划线的数字不符合变化规律。这一现象在实际应用中也是存在的。
4 结 论本文建立了锥形模型中方向关系的粗集表达模型,并定义了知识含量的测度用于度量锥形模型粗集表达的方向分类能力;构建了基于知识含量的近似精度和粗糙度,用于定量评价位置不确定性及方向系统划分粒度粗细引起的方向关系的不确定性。实验表明,本文提出的模型是定量评价多粒度空间方向关系不确定性的理想指标,可以避免采用误差传播理论研究不确定性的局限性。下一步的研究应在本模型中加入模型自身的不确定性,并考虑参考点位置不确定性的影响。
| [1] | Claramunt C, Theriault M. Fuzzy Semantics for Directionrelations Between Composite Regions[J]. Information Sciences, 2004,16(1):73-90 |
| [2] | Deng Min, Li Zhilin. A Statistical Model for Directional Relations Between Spatial Object[J]. Geoinformatica, 2008,12:193-217 |
| [3] | Yan Haowen, Chu Yandong, Li Zhilin, et al. A Quantitative Description Model for Direction Relations Based on Direction Groups[J]. Geoinformatica, 2006, 10:177-196 |
| [4] | Papadias D, Karacapilidis N, Arkoumanis D. Processing Fuzzy Spatial Queries:A Configuration Similarity Approach[J]. International Journal of Geographical Information Science, 1999, 13(2):93-118 |
| [5] | Du Shihong, Guo Luo. Modeling and Querying Approximate Direction Relations[J]. ISPRS Journal of Photogrammetry And Remote Sensing, 2010, 65(4):328-340 |
| [6] | Yan Haowen, Wang Zhonghui, Li J. An Approach to Computing Direction Relations Between Separated Object Groups[J]. Geoscientific Model Development, 2013(6):1 591-1 599 |
| [7] | Wang Miao, Hao Zhongxiao. Reasoning About the Inverse of Cardinal Direction Relation[J]. Information Technology Journal, 2010, 9(5):935-941 |
| [8] | Wang Zhonghui, Yan Haowen. An Improved Cone-Based Model for Describing Spatial Direction Relations[J]. Geomatics and Information Science of Wuhan University,2014,39(2):186-190(王中辉,闫浩文. 一种改进的锥形方向关系模型[J].武汉大学学报·信息科学版,2014,39(2):186-190) |
| [9] | Guo Jifa, Cui Weihong. Eight-Directions Fuzzy Asymmetric Division and Analysis of Its Uncertainty Conduced by Positioning Error of Reference Point[J]. Journal of Remote Sensing, 2010,14(5):879-885 |
| [10] | Chen Di, Zhu Xinyan, Zhou Chunhui, et al. A Fuzzy Description Method for Direction Relationship Based on Adaptive Sampling Granularity Model[J]. Acta Geodaetica et Cartographica Sinica,2013,42(3):359-366(陈迪,朱欣焰,周春辉,等. 基于自适应采样粒度模型的空间方向关系模糊描述方法[J].测绘学报,2013,42(3):359-366) |
| [11] | Guo Jifa, Cui Weihong, Liu Zhen, et al. Investigation of Uncertainty Integrative Description on Fuzzy Geographical Object[J]. Geomatics and Information Science of Wuhan University, 2010,35(1):46-50(郭继发,崔伟宏,刘臻,等. 模糊地理实体不确定性综合描述研究[J]. 武汉大学学报·信息科学版, 2010,35(1):46-50) |
| [12] | Li Deren. Some Thoughts on Spatial Data Uncertainty in GIS[J]. Journal of Zhengzhou Institute of Surveying and Mapping,2006,23(6):391-392 (李德仁.对空间数据不确定性研究的思考[J].测绘科学技术学报,2006,23(6):391-392) |
| [13] | Cicerone S, di Felice P. Cardinal Relations Between Regions with a Broad Boundary[C].The 8th ACM Symposium on Advances in Geographic Information Systems (GIS'00),New York, 2000 |
| [14] | Du Shihong, Wang Qiao, Wei Bin, et al. Spatial Orientational Relations Rough Reasoning[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4):334-338(杜世宏,王桥,魏斌,等. 空间方向关系粗糙推理[J].测绘学报,2003,32(4):334-338) |
| [15] | Xie Qi, Liu Dayou, Yu Qiangyuan, et al. Direction Relations Model Between Indeterminate Regions[J]. Journal of Jilin University of Science, 2006, 44(5):748-753 (谢琦,刘大有,虞强源,等.一种不确定区域间的方向关系模型[J].吉林大学学报(理学版),2006,44(5):748-753) |
| [16] | He Jianhua, Liu Yaolin, Yu Yan. Fuzzy Description Model for Uncertain Direction Relation[J]. Geomatics and Information Science of Wuhan University, 2008, 33(3):257-260) (何建华,刘耀林,俞艳. 不确定方向关系的模糊描述模型[J]. 武汉大学学报·信息科学版,2008,33(3):257-260) |
| [17] | Deng Min, Li Zhilin, Cheng Tao. Routh-Set Representation of GIS Data Uncertainties with Multiple Granularities[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(1):64-70 (邓敏,李志林,程涛.多粒度的GIS数据不确定性粗集表达[J].测绘学报,2006,35(1):64-70) |
| [18] | Cai Jianhong, Li Deren. Research on Cone-shaped Models of Cardinal Direction Relations Considering Positional Uncertainty of Multiple Spatial-scale Data[J]. Geomatics and Information Science of Wuhan University, 2007, 32(8):735-739(蔡剑红,李德仁. 多尺度下的不确定性空间方向锥形模型研究[J]. 武汉大学学报·信息科学版,2007,32(8):735-739) |
| [19] | Zhang Guoqin, Zhu Changqing, Li Guozhong. Measurement Indexes of Positional Uncertainty for Plane Line Segment Based on ε_m Model[J]. Geomatics and Information Science of Wuhan University, 2009,34(4):431-435(张国芹,朱长青,李国重. 基于ε_m模型的线元位置不确定性度量指标[J]. 武汉大学学报·信息科学版, 2009,34(4):431-435) |
| [20] | Liu Jiqin, Shi Kaiquan. An Uncertainty Measure for Rough Sets Based on Knowledge Capacity[J]. Computer Science, 2007, 34(7):171-173(刘纪芹,史开泉. 基于知识含量的粗糙集不确定性度量[J]. 计算机科学,2007,34(7):171-173) |
 2015, Vol. 40
2015, Vol. 40


