文章信息
- 张炳先, 王密, 潘俊
- ZHANG Bingxian, WANG Mi, PAN Jun
- 基于卡尔曼滤波的光学遥感影像高精度复原处理
- High Precision Image Restoration Based on Kalman Filter for Optical Remote Sensed Images
- 武汉大学学报·信息科学版, 2015, 40(7): 964-970
- Geomatics and Information Science of Wuhan University, 2015, 40(7): 964-970
- http://dx.doi.org/10.13203/j.whugis20130123
-
文章历史
- 收稿日期:2013-05-10
2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉, 430000
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
目前,国产光学卫星成像系统在平台稳定性控制、光学器件制造等方面与国外卫星存在一定差距,造成同等分辨率的国产光学卫星获取的影像清晰度较差,因此,有必要研究高质量的影像复原算法提高国产卫星影像质量。基于影像质量退化理论可知,如果成像系统的调制传递函数(MTF)能够精确测量得到,那么真实影像就可以被高质量恢复,研究高精度的MTF测量是提高影像复原质量的关键。近年来,卫星在轨运行时MTF的测量方法主要是采用刀刃法或脉冲法直接从成像数据中提取出来[1, 2],由于影像中刀刃靶标比脉冲靶标更易于被发现,且刀刃靶标对噪声的敏感度较低,在实际生产中,刀刃法使用更为频繁[3],然而,刀刃法仅仅解决了实验室测量数据,没有考虑大气和探元老化等因素而导致测量结果不准确的现象,却忽略了真实影像中噪声对刀刃靶标的影响[4],为了解决这一问题,国内外学者主要采用数学函数拟合的方式来消除噪声的干扰,例如,采用三次样条曲线拟合边缘扩展函数(ESF)[5];增加刃边的倾斜度来提高采样点个数[5];采取整平法将线扩展函数(LSF)两侧的波动直接置零[6]或取平均值。这类方法虽然在一定程度上抑制了干扰成分的影响,但由于只考虑了函数曲线的平滑度,并没有具体分析函数曲线抖动产生的具体原因,这样在抑制噪声影响的同时必然会剔除掉有用信息,引起MTF测量不准确,从而导致复原影像中噪声的增加。本文从质量改善的角度出发,在分析传统的MTF测量方法基础上,针对我国已经发射的高分辨率卫星影像数据的特点,以常用的刀刃法为研究对象,引入高斯步距拟合和卡尔曼(Kalman)滤波[7]的方法来提高MTF的测量精度,从而提高影像复原的质量。
1 基于卡尔曼滤波的MTF测量目前,MTF测量方法分为以下两类:① 实验室测量获取;② 遥感影像中计算得到。由于后者考虑了外在因素的影响,因此,其测量结果要优于实验室测量结果。但是根据Helder等人的研究结果发现[4],MTF对影像的信噪比比较敏感,卫星影像中的噪声成分会引起实际成像系统的线扩展函数两侧波动,这类波动会给MTF的测量输入错误的频率信息,因此,必须予以剔除。目前剔除采取的是LSF两侧置零或者取平均值的方式,这类方法并没有具体分析造成LSF波动的原因,直接采用数学拟合的方式将函数两侧整平,这可能会引入误差。本文以CBERS02B HR相机实测靶标数据以及人造零噪声靶标影像作为实验样本,求取LSF并对结果进行比对,如图 1所示,其中纵坐标表示相邻采样点灰度差,横坐标表示采样点个数计数值。

|
| 图 1 线扩展函数获取示意图 Fig. 1 Comparison of Acquired LSF Fromlab and Satellite Image |
通过对比可以发现,从实测靶标影像中得到的LSF两侧相较于从实验室靶标影像中获取的LSF两侧存在较大波动,但是同时可以发现,从实验室靶标影像中获取的LSF的两侧也并非完全平整。因此,采用传统的曲线两侧置平方法,会在去除噪声信息的同时去除部分纹理信息的影响导致LSF求解失真。由于LSF的物理函数模型是δ函数,因此,理论上的LSF可以通过高斯函数进行拟合[3],虽然拟合结果和真实值存在偏差,但是一维卡尔曼滤波可以通过理论值与实测含误差的值来获得真实的函数分布,借助这个特点,本文拟通过采取卡尔曼滤波来提高MTF测量的精度,具体的测量步骤如图 2所示。

|
| 图 2 基于卡尔曼滤波的MTF曲线测量方法流程图 Fig. 2 Diagram of MTF Measurement Based on Kalman Filter |
该方法中,线扩展函数高斯拟合的准确度是影响MTF精度的关键因素,因此,本文采用了高精度步距拟合来调整高斯拟合的结果,使高斯拟合的结果达到最优。
1.1 线扩展函数提取本文线扩展函数提取为实测线扩展函数提取,提取的基本步骤如下[2]。
1) 从成像数据中提取包含8°~20°倾斜角、刀刃状边缘的靶标影像。
2) 采用费米方程定位边缘点的位置,并采用最小二乘对提取出的边缘点进行处理获取亚像素级的边缘位置。
3) 以边缘位置为依据,对影像的行/列数据进行重采样,并将得到的结果合并,从而获取边缘扩展函数。
4) 对边缘扩展函数采取三次样条曲线进行拟合,对拟合结果求导获得线扩展函数。
1.2 线扩展函数高斯拟合高斯曲线的表达式为:
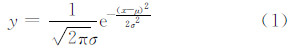
式中,μ为均值(即位置参数);σ为标准差。
由式(1)可知,高斯曲线拟合关键在于确定高斯分布的中心位置和高斯分布的离散度。对于受到噪声成分影响的近似高斯分布曲线,采用上述公式并运用迭代的方式进行拟合计算,计算量巨大且精度不高。为了简化计算复杂度,首先需要对高斯函数进行线性化处理,其处理公式为:
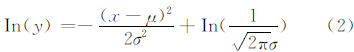
令In (y)=Y,x=X,则式(2)可以简化为:
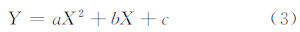
式(3)即为典型的二次方程,那么,对于高斯分布的拟合就变成了对二次曲线的拟合,其方程式为:
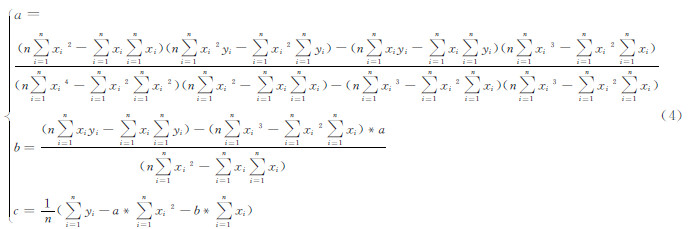
式中,n表示样本点的个数;xi和yi表示第i个样本点对应的x和y的坐标。由于解是二次曲线的拟合结果,因此,需要对其进行逆变换来获取所需的高斯曲线的拟合结果,其求解公式为:
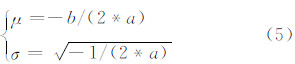
此处采用步距拟合的方式对高斯曲线拟合结果进行调整,寻找与实测曲线差异最小的结果,其拟合结果如图 3所示,其中纵坐标表示相邻采样点灰度的差值DN,横坐标表示采样点的个数计数值(像素)。
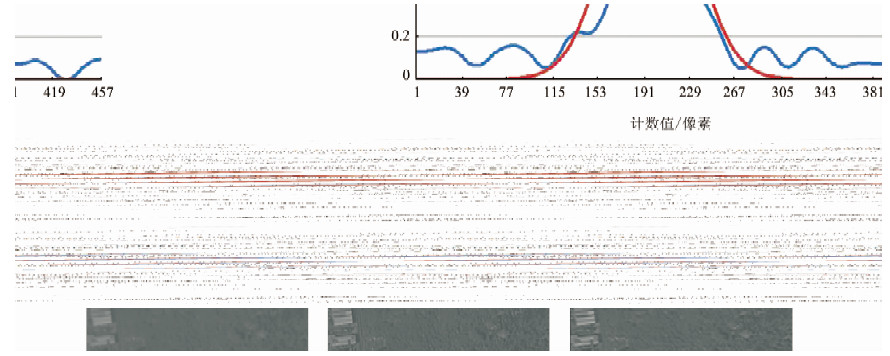
|
| 图 3 高精度高斯拟合线扩展函数 Fig. 3 Hight-precision Result of Gaussian Fitting to LSF |
卡尔曼滤波实质上属于最优化自回归数据处理算法[7],其基本原理是根据某一时刻得到的系统状态值和实际测量值来拟合出该时刻系统的真实估计,本文中,高精度高斯拟合结果即为状态分量,而实测的线扩展函数为实际测量值。卡尔曼滤波的核心是五个基本式(式(6)~式(8)和式(10)~式(11))。
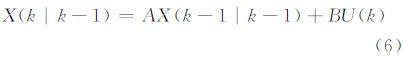
式中,X(k|k-1)是利用上一状态预测的结果;X(k-1|k-1)是上一状态的最优结果;U(k)是现在状态的控制量,如果没有,可以认定U(k)为0;A和B是预先的估算值,该值的大小决定了迭代收敛的次数以及收敛所需的时间。
在更新系统模型时,其对应的系统噪声方差也需要做同步更新,其更新公式为:
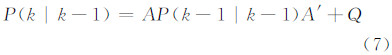
式中,P(k|k-1)是X(k|k-1)状态对应的噪声方差;P(k-1|k-1)是X(k-1|k-1)状态对应的噪声方差;对于一阶曲线LSF而言,A′是A导数;Q是系统过程中包含的噪声方差,为了简化处理,此处我们考虑的噪声为高斯白噪声,其系统过程中包含的噪声方差可以认为是0。
在获得现有状态的预测结果后,结合现在状态下的实测值Z(k)便可以得到当前状态的最优化估计值X(k|k):
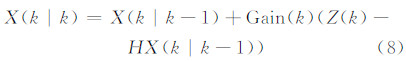
式中,Z(k)表示当前实测的LSF值;H为状态方程,结合LSF的优化模型,H表示为:
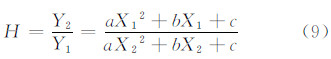
式中,Y表示的是高斯拟合的二次简化方程(式(3))。
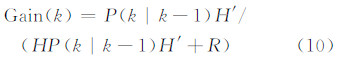
式中,直线方程H′为H的导数。在数学计算中,为了得到数据在函数收敛时的最优估计,需要令卡尔曼滤波不断的运行下去直至系统收敛,并不断更新状态k的噪声方差,使得噪声方差趋于最小,其方差更新公式为:
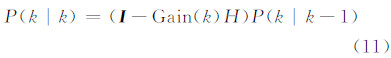
式中,I为单位矩阵。
可以发现,P的初始值选取会决定卡尔曼滤波的收敛速度。由于初始的样本数不够,所以刚开始获取的滤波结果并不准确,应该予以剔除,即线扩展函数初始的几个拟合样本点不能参与后续的MTF曲线生成,否则会引入较大误差。
1.4 MTF曲线和MTF矩阵生成在获得线扩展函数后,对线扩展函数做傅立叶变换,取傅立叶变换结果的模为各频率的值,并以第一个值为基准作归一化处理即得到MTF[5, 8, 9]。利用刀刃影像求得的MTF只是一维的MTF,而影像复原模型需要MTF矩阵,常规的处理方式是将水平MTF列向量乘以垂直MTF列向量,即
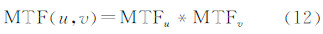
式中,MTFu为在水平方向频率u处的值;MTFv为在垂直方向频率v处的值;MTF(u,v)为二维频率坐标为(u,v)处的值。
这种方法求得的矩阵在45°方向的值与水平或垂直方向差别很大,因此,本文中采用文献[10]提出的矩阵构造方法,取水平与垂直方向0.5频率处值的平均值再衰减90%作为45°方向0.5频率处的值; 再根据水平与垂直方向向量之间的比例关系进行插值,得到二维矩阵。
采用传统的两侧置平方法[4, 6]和卡尔曼滤波方法获取的矩阵值的示意图(单象限区间的截取图)如图 4所示,高度坐标表示归一化后的频率值,平面坐标表示水平和垂直两个方向的采样点的个数计数值。
对比图 4(a)和4(b)发现,置平方式会改变靶标影像中各个频率成分之间的关系,导致求取后得出的矩阵波动较大,出现了略小于0的值。而采用卡尔曼滤波的方法获取的矩阵,其变化较为平缓,符合靶标影像的边缘连续变化的特征。

|
| 图 4 MTF矩阵获取示意图 Fig. 4 Comparison of Acquired MTF Curve by Traditional Method and Our Proposed Method |
基于MTF 的影像复原的数学通用模型可以表示为[11]:
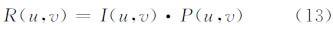
式中,R(u,v)为复原影像的频谱;I(u,v)为原始影像频谱;P(u,v)为选取的滤波器算子;·表示卷积运算。考虑到复原效果和复原速度,本文采用的滤波算子是维纳滤波算子,其具体形式为:
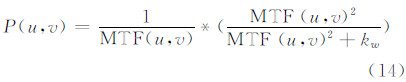
式中,kw是与影像信噪比有关的先验常数(本文取值0.02);MTF(u,v)为二 维MTF矩阵。
3 实验与分析资源一号02B卫星HR相机上天后,其成像系统在轨运行的MTF较实验室测量获取的MTF而言,有了明显下降,影响影像后续的目标判读等应用,为了验证本文算法的有效性,试验采用了中国资源卫星应用中心提供的资源1号02B HR成像数据,并将本文算法获取的MTF矩阵与传统的算法获取的MTF矩阵分别用于基于MTF补偿(MTFC)的复原算法中,并对复原结果进行了比较分析。图 5、图 6显示了本文的试验结果。
水域区域在可见光卫星影像中属于低亮度区域,探元在该区域的光电响应属于非线性响应,其响应函数通常不稳定[12],因此,这段区域的成像数据会含有大量的暗噪声,若对MTF中的频率成分测量不准确,便会导致复原后的影像中噪声成分被增强。如图 5(e)所示,采用传统的MTFC影像复原方法后,复原影像中的噪声被明显增强,而采用本文算法获得的复原影像中噪声成分没有被放大。
城区在可见光卫星影像中属于中等亮度区域,探元在该区域的光电响应属于线性响应,影像中边缘纹理复杂,若对MTF中的频率成分测量不准确,会导致复原后的影像中边缘信息被错误增强。如图 6(e)所示,采用传统方式复原的影像中车辆信息的边缘明显没有采用本文方式复原的影像中车辆信息的边缘丰富,采用传统方式复原的影像对后续应用尤其是地物判读会产生不利的影响。
为了进一步定量说明,本文引入了表征影像细节特征的边缘能量、纹理对比度、奈奎斯特频率值作为评价标准,比较截取影像局部放大图之间的差异,其中边缘能量、纹理对比度的计算公式如式(15)~式(16)所示,其具体结果参见表 1所示。
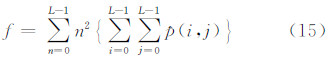
式中,f表示边缘能量;i和j为图像行列号,|i-j| =n,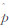 (i,j)为归一化的灰度共生矩阵元素。
(i,j)为归一化的灰度共生矩阵元素。
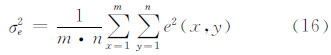
式中,σe2表示纹理对比度;m和n为图像行列号;e2(x,y)计算方法为:

式中,f(x,y)表示图像中以(x,y)为中心的3像素×3像素大小的灰度矩阵; E 1和 E 2的表达式为:

| 原始影像 | 传统方法 | 本文方法 | ||
| 水域区域 | 边缘能量 | 0.426 563 | 1.307 858 | 1.461 346 |
| 纹理对比度 | 6.577 691 | 20.077 54 | 20.815 83 | |
| 奈奎斯特频率 | 0.027 6 | 0.127 96 | 0.153 84 | |
| 城市区域 | 边缘能量 | 6.755 819 | 33.235 6 | 57.733 5 |
| 纹理对比度 | 221.638 8 | 520.111 3 | 540.069 | |
| 奈奎斯特频率 | 0.103 5 | 0.157 4 | 0.216 9 |
根据试验结果可以发现无论是采用传统的MTFC影像复原方法还是采用本文算法,复原后的影像其边缘能量、纹理对比度、奈奎斯特频率值较原有影像都有所提升。但是采用本文算法的影像,其复原后的纹理信息要明显多于采用传统MTFC影像复原算法复原的影像,这个结果和图 5、图 6中的视觉效果一致。分析造成该种现象的原因,主要是由于传统的MTFC影像复原算法对于点扩散函数的估算存在偏差,导致采用传统的影像复原算法对影像进行复原后,影像中无效信息被明显放大。综上所述,本文算法较传统的MTFC影像复原方法而言,具有一定的优势,能够更好的保留影像中的有用信息。

|
| 图 5 水域影像复原结果对比图 Fig. 5 Comparison of Restoration Results by Water Regional Image |

|
| 图 6 城市影像复原结果对比图 Fig. 6 Comparison of Restoration Results by City Regional Image |
本文在研究传统的MTFC影像复原算法的基础上,结合国产高分辨率卫星成像数据的特点,提出了一种基于卡尔曼滤波的高精度影像复原处理方法。该算法解决了传统的基于靶标影像的MTF测量方法中噪声干扰的问题。通过中国资源卫星应用中心提供的资源1号02B HR数据的实验验证了本文算法的有效性,处理后影像质量得到明显改善,特别是在水域等少纹理区域,本文算法能更好的抑制水域中的噪声;在城区,复原影像的细节信息得到明显改善,尤其是车辆的边缘处。
致谢:本文数据获取得到资源卫星应用中心相关部门的大力支持,同时资源卫星应用中心龙小祥、钟慧敏在数据验证方面提供了帮助和支持,在此表示衷心感谢!
| [1] | Helder D, Choi T, Rangaswamy M. In-flight Characterization of Spatial Quality Using Point Spread Functions[J]. International Society for Photogrammetry and Remote Sensing, 2004, 2:149-170 |
| [2] | Choi T. IKONOS Satellite On-orbit Modulation Transfer Function Measurement Using Edge and Pulse Method[D]. South Dakota State:South Dakota State University, 2002 |
| [3] | Qiu Xiaojun. The Study of MTF Image Restoration Method[D]. Nanjing:Nanjing University of Science and Technology, 2006 (邱晓君.基于MTF遥感影像恢复技术研究[D]. 南京:南京理工大学, 2006) |
| [4] | Helder D. On-orbit Modulation Transfer Function Measurements for IKONOS and QuickBird[D]. South Dakota State:South Dakota State University, 2006 |
| [5] | Dennis L. IKONOS Satellite in Orbit Modulation Transfer Function Measurement Using Edge and Pulse Method[D]. South Dakota State:South Dakota State University:2002 |
| [6] | Ge Ping, Wang Mi, Pan Jun, et al. A Study of Adaptive MTF Image Restoration of High Resolution TDI-CCD Image Data[J]. Remote Sensing for Land & Resources, 2010(4):23-28(葛平, 王密, 潘俊, 等.高分辨率TDI-CCD成像数据的自适应MTF影像复原处理研究[J].国土资源与遥感, 2010(4):23-28) |
| [7] | Jiang Peng, Ye Shirong, He Shujing, et al. Groud-based GPS Tomography of Wet Refractivity with Adaptive Kalman Filter[J]. Geomatic and Information Science of Wuhan University, 2013, 38(3):299-302 (江 鹏, 叶世榕, 何书镜, 等.自适应Kalman滤波用于GPS层析大气湿折射率[J].武汉大学学报·信息科学版, 2013, 38(3):299-302) |
| [8] | Yue Qingxing, Qiu Zhenge, Jia Yonghong, et al. Research on Image Simulation of Satellite Three-Line-Array TDI-CCD Camera[J]. Geomatic and Information Science of Wuhan University, 2010, 35(12):1 427-1431(岳庆兴, 邱振戈, 贾永红, 等. 三线阵TDI CCD相机在轨成像数学仿真方法[J]. 武汉大学学报·信息科学版, 2010, 35(12):1 427-1 431) |
| [9] | Forster B C, Best P. Estimation of SPOT P-mode Point Spread Function and Derivation of a Deconvolution Filter[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1994, 49(6):32-42 |
| [10] | Gu Xingfa, Li Xiaoying, Min Xiangjun, et al. On-orbit Measurement and Compensation of MTF for CBERS 02B CCD Images[J]. Science in China Ser E Information Science, 2005, 35(B12):26-40 (顾行发, 李小英, 闵祥军, 等.CBERS 02B卫星CCD相机MTF在轨测量及影像MTF补偿[J].中国科学, 2005, 35(B12):26-40) |
| [11] | Fonseca L M G, Prasad G S D, Mascarenhas N D A. Combined Interpolation Restoration of Land-sat Images Through FIR Filter Design Techniques[J]. International Journal of Remote Sensing, 1993, 14(13):2 547-2 561 |
| [12] | Pan Zhiqiang, Gu Xingfa, Liu Guodong, et al. Relative Radiometric Correction of CBEERS-01 CCD Data Based on Detector Histogram Matching[J]. Geomatic and Information Science of Wuhan University, 2005, 30(10):925-927(潘志强, 顾行发, 刘国栋, 等.基于探元直方图匹配的CBERS-01星CCD数据相对辐射校正方法[J].武汉大学学报·信息科学版, 2005, 30(10):925-927) |
 2015, Vol. 40
2015, Vol. 40


