文章信息
- 肖巍峰, 邓敏, 李朝奎
- XIAO Weifeng, DENG Min, LI Chaokui
- 三维点云多尺度等值线模型Morphing变换方法研究
- Multi-scale Contour Model Transformation of 3D Point Cloud Based on Morphing Technology
- 武汉大学学报·信息科学版, 2015, 40(7): 957-963
- Geomatics and Information Science of Wuhan University, 2015, 40(7): 957-963
- http://dx.doi.org/10.13203/j.whugis20140107
-
文章历史
- 收稿日期:2014-02-16
2. 湖南科技大学测绘工程系, 湖南 湘潭, 411201
2. Department of Surveying-Engineering, Hunan University of Science and Technology, Xiangtan 411201, China
Morphing技术又称为连续变形(continuous deformation)技术,起源于20世纪90年代,最初用于处理图像渐变,现已成为处理视图变形的一种重要方法。该技术可实现从源图像到目标图像的平滑渐变,是一种兼顾形状和颜色的图像内插方法,在动画制作、图像压缩及图像重构等领域有广泛应用[1, 2, 3, 4]。三维点云,即采用三维激光扫描技术获得的数据,精度非常高,地面激光扫描一般可达到mm级的采样间隔。利用高精度的三维点云数据来构建物体表面的多尺度等值线模型,使得用户可以获得目标物体不同详细程度的表面信息。对于离散的矢量数据集,其等值线生成方法一般可分为规则数据场的等值线生成和不规则数据场的等值线生成两类。规则数据场等值线的生成,一般采用的是MC(marching cubes)[5]、MT(marching tetrahedral)[6]和剖分立体法[7],主要应用于CT或核磁共振(MRI)等医学图像领域。利用激光扫描技术获得的三维点云数据是不规则的空间数据集,不能直接采用上述方法来生成等值线。不规则数据场等值线的生成,典型的方法是首先生成不规则数据场的Delaunay三角网,然后用等值线内插、追踪方法计算和连接等值点[8, 9]。诸多方法中比较有代表性的是利用地性线及拓扑关系直接求取等值线法[10]和利用已有的等值线内插新的等值线法[11],这两种方法都能满足一定条件下等值线的生成。然而,对于点云,并不能直接采用这类方法。因为这类方法首先需生成三维点云的表面模型,构建三维Delaunay三角网格,但该技术至今还有很多难点没有解决,基于最大-最小角判断的对角线交换规则不成立,基于外接圆规则判断Delaunay三角化也难以获得高质量网格;其次,利用这类方法生成的等值线,矢量数据集必须满足一定的条件才能实现,而点云数据并不满足。吴杭彬[12]等采用迭代凸包的方法来提取激光扫描数据的分层多细节等值线,但从简单细节到复杂细节的等值线提取,要经过多次迭代凸包,算法效率低,而且针对某一细节等值线,没有一个量化指标来衡量其细节表达程度。
针对当前三维点云等值线模型构建方法存在的缺陷,本文借鉴Morphing技术思想,提出了一种三维点云多尺度等值线模型Morphing变换方法。Morphing尺度变换模式的主要特点是采用两个不同尺度数据集对尺度变换进行两端控制,近年来广泛应用于地图制图领域[13],其中一个主要应用是采用Morphing技术生成多尺度地图数据。 根据数据对象的不同,Morphing变换可以分为基于矢量数据和栅格数据的Morphing变换。目前,基于矢量数据的Morphing变换主要集中于道路、河流等线状要素进行内插,以生成所需尺度线状要素形态[14]。而利用该技术生成三维点云等值线模型这种有点集筛选的尺度变换情况,研究相对较少。鉴于此,本文将基于Morphing技术来探讨三维点云等值线模型的变换方法。
1 基于Morphing的分层点云等值线多尺度变换 1.1 基本策略由于点云数据通常是以不规则的三维点集形式存在,而本文方法涉及的等值线生成是以层为基本单元,因此,首先分析三维点云的空间分布情况,按一定的间隔(或厚度)垂直于某一坐标轴方向分层,建立点云分层模型。然后分别处理每个点云层,处理流程如图 1所示。由分层点集生成的凸包多边形虽然细节表达简单,但其拓扑结构可以得到保证,形成的等值线折线不会交叉,可以将其视为该层点集表示的等值线折线的一个近似。显然,凸包顶点集是分层点集的一个子集,该层还有一些离散点没有被包括在该折线上,使得等值线折线细节表达过于简单。因此,需要将这些点归类到折线上,即确定每个点属于折线上的某条边。为了更精确地表达分层等值线 ,需要按照一定的准则对归类后的离散点进行选取处理,逐步增加到等值线上,直到当前的等值线包含该层所有的点。为此,引入变换程度参数t,根据t值输出相应的变换结果。值得注意的是,变换程度参数t (t∈[0, 1])是一个与等值线多分辨率表达有关的参数。当t=0时,变换结果即为最低细节等值线,也就是凸包多边形表达的等值线;当t=1时,变换结果即为最高细节等值线,即连接分层所有点集的等值线;而t从0变化到1的过程则对应着最低细节等值线变换到最高细节等值线的过程。最后,经过折线拟合得到光滑的等值线。
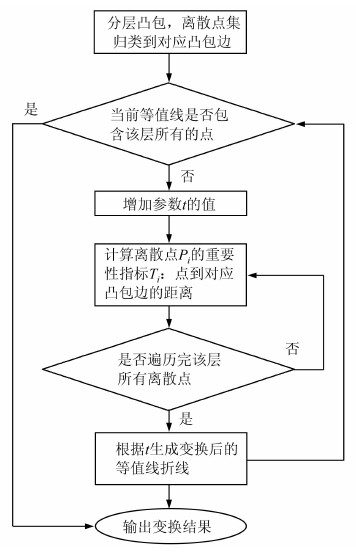
|
| 图 1 点云层数据处理流程 Fig. 1 Flowchart of Processing Data of Point Cloud Layer |
以某一层数据来说明该层等值线的Morphing变换过程,其他层数据处理过程类似。假设某层点集LayerPts={ P0,P1,…,Pt-1},t为点的个数。定义数组LayerPts,保存该层点集。
1) 采用Graham扫描法建立其凸包多边形作为表达该层最低细节的等值线,将其称为最小尺度等值线。定义数组SmallScalePts,记录按逆时针排列好的凸包顶点集。 将LayerPts中的凸包点集删除掉,剩下的就是该层的离散点集。
2) 将LayerPts中的点归类到对应的凸多边形的某条边上。如果离散点Pi投影到凸包边 上,其投影落在边的内部,并且Pi到
上,其投影落在边的内部,并且Pi到 边距离最近,称Pi属于
边距离最近,称Pi属于 边,将Pi到
边,将Pi到 的距离赋值给Pi的成员m_DistToEdge,将
的距离赋值给Pi的成员m_DistToEdge,将 的索引号赋值给Pi的成员m_edgeIndex。如图 2所示,
的索引号赋值给Pi的成员m_edgeIndex。如图 2所示, 、
、 、
、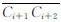 是当前凸多边形的边,Pj为尚未归类到当前凸多边形某条边上的一个离散点。Pj在这3条边上的垂直投影都分别落在对应边内部,但该点到
是当前凸多边形的边,Pj为尚未归类到当前凸多边形某条边上的一个离散点。Pj在这3条边上的垂直投影都分别落在对应边内部,但该点到 边距离最短,因此,Pj归类于
边距离最短,因此,Pj归类于 边。
边。

|
| 图 2 当前的等值线和待定点 Fig. 2 Current Contour and Undetermined Points |
3) 判断Pj在 边上的投影是否在
边上的投影是否在 边内部。求出Pj到
边内部。求出Pj到 边的投影,记为PVj,其平面坐标为(vxj,vyj),假设Ci、Ci+1的平面坐标分别为(xi,yi)和(xi+1,yi+1)。如果
Min(xi,xi+1) < vxj < Max(xi,xi+1)并且Min(yi,Ci+2yi+1) < vyj < Max(yi,yi+1),则Pj在
边的投影,记为PVj,其平面坐标为(vxj,vyj),假设Ci、Ci+1的平面坐标分别为(xi,yi)和(xi+1,yi+1)。如果
Min(xi,xi+1) < vxj < Max(xi,xi+1)并且Min(yi,Ci+2yi+1) < vyj < Max(yi,yi+1),则Pj在 边上的投影在
边上的投影在 边内部,其中Min、Max分别表示最小值、最大值函数。假定点Pj-2~Pj+2是该层的属于边
边内部,其中Min、Max分别表示最小值、最大值函数。假定点Pj-2~Pj+2是该层的属于边 的所有离散点,并且点到边
的所有离散点,并且点到边 的距离分别赋值给其成员变量m_DistToEdge,成员变量m_edgeIndex值就是
的距离分别赋值给其成员变量m_DistToEdge,成员变量m_edgeIndex值就是 的索引号。
的索引号。
本文通过离散点的选取将最小尺度等值线(即凸多边形) Morphing变换成最大尺度等值线(即包含该层所有点的多边形)。定义SmallScaleContour表示最小尺度等值线折线,LargeScaleContour表示最大尺度等值线折线。传统的Morphing变换需要初始端两个不同尺度的数据进行控制,而且关于线状要素间的Morphing变换技术相对比较成熟。本文采用一定的方法,将等值线(即多边形)之间的Morphing变换转换成线状要素间的Morphing变换,等值线的匹配转换成线状要素的匹配。为了方便起见,将凸包顶点称为断点,这样,SmallScaleContour被断点分割成多条线段,如断点 Ci、Ci+1将等值线分割成线段 。然而,刚 开始LargeScaleContour并不存在,而是以散点形式存在。如果最终形成LargeScaleContour,则断点将其分割成多条折线或线段,显然,这些折线或线段的端点是断点。SmallScaleContour中的线段匹配着LargeScaleContour中具有相同断点的折线或线段。为了便于描述,将包含点 Pj-2~Pj+2的折线
。然而,刚 开始LargeScaleContour并不存在,而是以散点形式存在。如果最终形成LargeScaleContour,则断点将其分割成多条折线或线段,显然,这些折线或线段的端点是断点。SmallScaleContour中的线段匹配着LargeScaleContour中具有相同断点的折线或线段。为了便于描述,将包含点 Pj-2~Pj+2的折线 记为
记为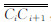 ,则线段
,则线段 匹配折线
匹配折线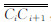 。等值线中其他线段与线段或线段与折线之间匹配关系的建立类似,这样等值线的匹配就转换成了线状要素的匹配。
。等值线中其他线段与线段或线段与折线之间匹配关系的建立类似,这样等值线的匹配就转换成了线状要素的匹配。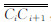 首先并不存在,而是要由
首先并不存在,而是要由 通过离散点Pj-2~Pj+2的选取Morphing变换而成。
通过离散点Pj-2~Pj+2的选取Morphing变换而成。 变换到
变换到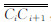 的过程其实就是简单线状要素变换到复杂线状要素的过程,是线状要素综合的逆过程。显然,离散点到对应凸包边距离的长短可以反映该点所在位置等值线的弯曲程度,距离越长,则弯曲越厉害。因此,以离散点到其对应凸包边距离作为离散点的重要性指标,距离越大,则越重要。输入t,可按如下步骤来选取离散点Pj-2~Pj+2。
的过程其实就是简单线状要素变换到复杂线状要素的过程,是线状要素综合的逆过程。显然,离散点到对应凸包边距离的长短可以反映该点所在位置等值线的弯曲程度,距离越长,则弯曲越厉害。因此,以离散点到其对应凸包边距离作为离散点的重要性指标,距离越大,则越重要。输入t,可按如下步骤来选取离散点Pj-2~Pj+2。
① 计算每个离散点的选取时机参数:为了得到Morphing变换效果,必须讨论变换程度参数 t与离散点选取时机的关系。假设需选取离散点Pj-2~Pj+2中,其到 的最小距离为MinDistance,最大距离为MaxDistance,则容易得到各离散点的选取时机参数Ti为:
的最小距离为MinDistance,最大距离为MaxDistance,则容易得到各离散点的选取时机参数Ti为:
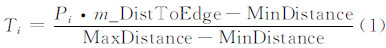
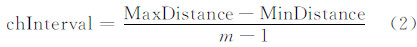
 的m_ chInterval。然后对MinDistance、MaxDistance修正如下:
的m_ chInterval。然后对MinDistance、MaxDistance修正如下:

 的m_MinDist、m_MaxDist。采用修正后的MinDistance、MaxDistance代入式(1),重新计算出各离散点的选取时机。值得注意的是,当m=1时,即属于某条边的离散点总数只有1个时,不妨定义t≥0.5时,该点被选取。
的m_MinDist、m_MaxDist。采用修正后的MinDistance、MaxDistance代入式(1),重新计算出各离散点的选取时机。值得注意的是,当m=1时,即属于某条边的离散点总数只有1个时,不妨定义t≥0.5时,该点被选取。
② 将被选取的点加入到当前等值线中,并局部更新等值线:不妨假设有Pj-1、Pj、Pj+2 3点需加入,其更新过程如图 3所示。可按如下方法进行:首先,断开 ,将Pj-1加入中间,连接Ci、Pj-1和Pj-1、Ci+1。然后,按上述分类方法判断点Pj属于边
,将Pj-1加入中间,连接Ci、Pj-1和Pj-1、Ci+1。然后,按上述分类方法判断点Pj属于边 还是
还是 ,本例中Pj属于
,本例中Pj属于 ,断开
,断开 ,Pj加入中间,连接Pj-1、Pj和Pj、Ci+1。最后,判断Pj+2属于
,Pj加入中间,连接Pj-1、Pj和Pj、Ci+1。最后,判断Pj+2属于 、
、 还是
还是 ,同样的方法断开某条边,将Pj+2加入,重新连接,完成局部等值线更新。将被选取的点从 数组LayerPts中删除。
,同样的方法断开某条边,将Pj+2加入,重新连接,完成局部等值线更新。将被选取的点从 数组LayerPts中删除。

|
| 图 3 局部等值线更新 Fig. 3 Updating Local Contour |
③ 遍历其他凸包边,重复步骤① 、步骤②,完成该层等值线的更新,得到参数t对应的变换后的等值线,并保存为CurrentContour。
增大t值,将数组LayerPts中的点根据m_edgeIndex值将其归类到对应的凸包边,节省了重复归类计算的时间。不妨还是以  为例,将LayerPts中m_edgeIndex值为
为例,将LayerPts中m_edgeIndex值为 索引号的点提取出来。由Ti≥1-t,根据式(1),可以计算出离散点到边
索引号的点提取出来。由Ti≥1-t,根据式(1),可以计算出离散点到边 的距离阈值,将离散点中距离值(m_ DistToEdge)大于距离阈值的点提取出来,按照步骤②加入到CurrentContour以Ci、Ci+1为断点的折线上,局部更新等值线。同时,将加入的点在LayerPts中删除掉。其他离散点按类似方法加入,完成该层等值线的更新,得到参数t对应的变换后的等值线,保存为CurrentContour。继续增大t值,如此循环迭代,直到数组LayerPts为空,得到包含该层所有点的等值线,记为LargeScaleContour,算法结束。
的距离阈值,将离散点中距离值(m_ DistToEdge)大于距离阈值的点提取出来,按照步骤②加入到CurrentContour以Ci、Ci+1为断点的折线上,局部更新等值线。同时,将加入的点在LayerPts中删除掉。其他离散点按类似方法加入,完成该层等值线的更新,得到参数t对应的变换后的等值线,保存为CurrentContour。继续增大t值,如此循环迭代,直到数组LayerPts为空,得到包含该层所有点的等值线,记为LargeScaleContour,算法结束。
§1.2得到的等值线是折线形状,必须经过折线拟合后才能得到平滑的等值线。折线拟合方法有很多种,比如样条拟合、三次多项式法、余弦函数差值等。本文将采用样条拟合方法。
2 实例验证基于Morphing的三维点云多尺度等值线模型构建法只需要经过一次凸包算法,生成一个最小尺度等值线模型,通过计算离散点的选取时机参数完成点的选取,就可以生成连续尺度变换的等值线模型。文献[12]的迭代凸包法从最低尺度等值线模型变换到最高尺度等值线模型,要经过多次凸包迭代,显然,本文方法具有明显的速度优势。为了验证本文方法的有效性和实用性,在CPU2.0 GHz、内存为1 G的PC机上,分别采用规则点云数据模型和散乱点云数据模型进行了实验,生成了5个尺度的等值线及等值线模型。
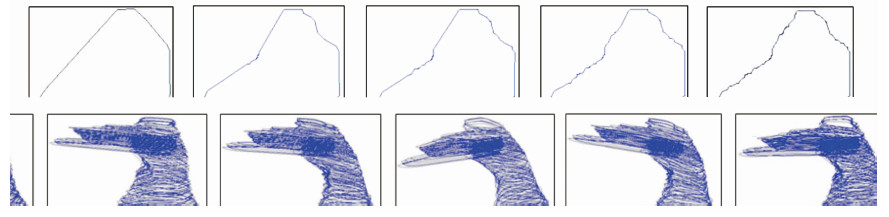
2.1 规则点云数据算例规则点云数据如图 4所示。图 4(a)是右心 室点云模型,包含点数为22 481,Z坐标范围是 0~53 mm,按Z坐标轴方向分层存储,每层间隔dz=0.5 mm,总计分为106层。图 4(b)为Z=20 mm的层,总计点数为277,其基于Morphing的多尺度等值线变换结果如图 5所示,其中t表示内插程度参数,n表示点数,s表示面积,单位是mm2。t=0.25时,占总点数之比为44.4%,相比较于精确面积,其面积变化之比为3%,可见,用较少的点能较准确地表达等值线的形状。从图 5可以明显地看出,t从1变化到0的过程中,等值线细节表达越来越丰富,而且能保障其拓扑结构,没有交叉。图 6是基于Morphing的右心室点云的多尺度等值线模型变换结果图。

|
| 图 4 右心室点云 Fig. 4 Point Cloud of the Right Ventricle |
|
| 图 5 Z=20 mm层等值线Morphing结果 Fig. 5 Contour Results Obtained by Morphing for Layer Z=20 mm |

|
| 图 6 右心室点云等值线模型Morphing结果 Fig. 6 Contour Model Results Obtained by Morphing for Right Ventricle Point Cloud |

|
| 图 7 佛像点云 Fig. 7 Point Cloud of the Buddhist Image |
|
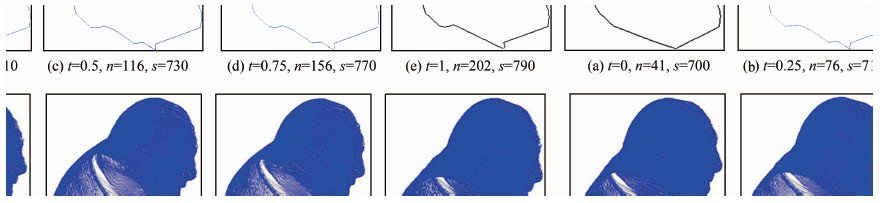
| 图 8 Z=0.200 5 m层等值线Morphing结果 Fig. 8 Contour Results Obtained by Morphing for Layer Z=0.200 5 m |

|
| 图 9 佛像点云等值线模型Morphing结果 Fig. 9 Contour Model Results Obtained by Morphing for Buddhist Image Point Cloud |
从图 6、图 9可以看出,在没有先验等值线知识和建立点云对象模型的条件下,借鉴Morphing思想采用计算离散点的选取时机参数的方法对点进行选取,能有效地连接分层点集,形成多尺度、连续变化的点云等值线模型。相比较于文献[12]的迭代凸包方法,本文方法具有明显的速度优势,两种方法生成最高尺度等值线模型(即t=1)的运行时间对比结果如表 1所示;同时,本文方法生成的中间尺度等值线多边形面积更接近于最高尺度等值线多边形面积,分别取右心室模型的Z=20 mm等值线和佛像点云模型的Z=0.200 5 m等值线进行对比试验,其对比结果如图 10所示,其中横坐标表示等值线所包含的顶点数目,纵坐标表示面积变化比。从图 10可以看出,本文方法的面积变化比更小,表示在生成中间尺度等值线的时候,本文方法对点的选取更合理。
| 方法 | 模型 | 点数 | 分层凸包时间/s | 散点归类及Morphing变换时间/s | 折线拟合时间/s | 总时间/s | 迭代凸包法总时间/s |
| 基于Morphing法 | 右心室 | 22 481 | 0.64 | 0.51 | 0.48 | 1.63 | 5.43 |
| 佛像 | 58 422 | 1.68 | 1.36 | 1.28 | 4.32 | 15.36 |

|
| 图 10 等值线面积变化比对比结果 Fig. 10 Comparison Result of the Ratio of Contour Area Change |
本文提出了一种三维点云多尺度等值线模型的Morphing变换方法,借鉴Morphing变换思想,在对点云数据分层的基础上,能有效地构建多尺度、连续变化的点云等值线模型。通过实验对比和例证,本文方法比文献[12]的迭代凸包法具有以下优势:① 没有迭代凸包运算过程,提高了算法效率;② 生成中间尺度等值线时,点的选取更加合理。
必须说明的是,本文方法对原始点云数据采样密度要求比较高,如果采样间隔过大(如cm级),那么在某一坐标轴方向按一定间隔分层后,每层的点云数目将比较少,不足以有效地表达该层等值线的形状。同时,分层坐标轴方向上每层只能有一条等值线,如果超过一条,需要首先将点云数据分割,然后在各分割区域单独构建等值线。因此,对本文所提算法的适应条件有待进一步的深入研究。
| [1] | Li Z L, Wong M. Animating Basic Operations for Digital Map Generalization with Morphing Techniques[J]. The International Archives of the Photogrammetry, Remote Sensing and Spatial I-nformation Science, 2008, 35(B2):637-642 |
| [2] | Li Jingzhong. An Object-Oriented Model for Map Data Multiple Representation over Scale Space[D]. Wuhan:Wuhan University, 2009(李精忠. 尺度空间地图多重表达的面向对象数据模型研究[D]. 武汉:武汉大学, 2009) |
| [3] | Ai Tinghua, Li Jingzhong. The Lifespan Model of GIS Data Representation over Scale Space[J].Geomatics and Information Science of Wuhan University, 2010, 35(7):757-762(艾廷华, 李精忠. 尺度空间中GIS数据表达的生命期模型[J]. 武汉大学学报·信息科学版, 2010, 35(7):757-762) |
| [4] | Li Xudong. Image Morphing Method for Facial Expression Image and Animation Synthesis[J].Geomatics and Information Science of Wuhan University, 2007, 32(9):796-799(李旭东. 用于人脸表情图像与动画合成的图像变形方法.[J]. 武汉大学学报·信息科学版, 2007, 32(9):796-799) |
| [5] | Lorensen W E, Cline H E. Marching Cubes:A High-Resolution 3D Surface Construction Algorithm[J]. Computer Graphics, 1987, 21(4):163-180 |
| [6] | Giertsen C. Volume Visualization of Sparse Irregular Meshes[J]. IEEE Computer Graphics & Application, 1992, 12(2):40-50 |
| [7] | Cline H E, Lorensen W E. Two Algorithms for Three Dimensional Reconstruction of Tomograms[J]. Medical Physics, 1988, 15(3):320-336 |
| [8] | Li Shanshan, Wu Xiaoping, Tian Yanfeng. Improvement on the Iterated Closest Contour Point Matching Algorithm Using Underwater Gravity Anomalies[J].Geomatics and Information Science of Wuhan University, 2011, 36(2):226-230(李珊珊, 吴晓平, 田颜锋.水下重力异常最近等值线迭代匹配算法的改进[J]. 武汉大学学报·信息科学版, 2011, 36(2):226-230) |
| [9] | Qi Shuhua, Gu Zhongyu, Brown D, et al. Inundation Extent Mapping for Poyang Lake with Digital Elevation Models[J].Geomatics and Information Science of Wuhan University, 2010, 35(7):857-862(齐述华, 顾中宇, Brown D, 等.基于数字高程模型的鄱阳湖淹水范围制图研究[J]. 武汉大学学报·信息科学版, 2010, 35(7):857-862) |
| [10] | Zhao Fulai, Hao Xiangyang. A Research on Contour Plotting Based on Bone Lines[J]. Acta Geodaetica et Cartographica Sinica, 1999(4):345-351(赵夫来, 郝向阳. 根据地性线绘制等高线的研究[J].测绘学报, 1999(4):345-351) |
| [11] | Gong Youliang, He Yuhua. A Practical Contour Interpolation Algorithm[J]. Journal of Instiute of Surveying and Mapping, 2002, 19(1):36-40(龚有亮, 何玉华. 一种实用的等高线内插算法[J].测绘学院学报, 2002, 19(1):36-40) |
| [12] | Wu Hangbin, Liu Chun. Point Cloud-Based Stratified Contour Extraction and its Multi-LoD Expression with Ground Laser Range Scanning[J]. Journal of TongJi University(Natural Science), 2009, 37(2):267-271(吴杭彬, 刘春. 激光扫描数据的等值线分层提取和多细节表达[J]. 同济大学学报(自然科学版), 2009, 37(2):267-271) |
| [13] | Peng Dongliang, Deng Min, Zhao Binbin, et al. Multi-scale Transformation of River Networks Based on Morphing Technology[J]. Journal of Remote Sensing, 2012, 16(5):961-968(彭东亮, 邓敏, 赵彬彬, 等. 河网多尺度Morphing的变换方法研究[J].遥感学报, 2012, 16(5):961-968) |
| [14] | N llenburg M, Merrick D, Wolff A, et al. Morphing Polylines:A Step Towards Continuous Generalization[J]. Computers, Environment and Urban Systems, 2008, 32:248-260 |
 2015, Vol. 40
2015, Vol. 40


