文章信息
- 薛树强, 杨元喜
- XUE Shuqiang, YANG Yuanxi
- 抗差高斯-雅克比组合平差法
- Robust Gauss-Jacobi Combinatorial Adjustment
- 武汉大学学报·信息科学版, 2015, 40(7): 932-937
- Geomatics and Information Science of Wuhan University, 2015, 40(7): 932-937
- http://dx.doi.org/10.13203/j.whugis20130247
-
文章历史
- 收稿日期:2013-06-17
2. 中国测绘科学研究院, 北京, 100830;
3. 地理信息工程国家重点实验室, 陕西 西安, 71005;
4. 西安测绘研究所, 陕西 西安, 710054
2. Chinese Academy of Surveying and Mapping, Beijing, 100830, China;
3. National Key Laboratory for Geo-information Engineering, Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
4. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
抗差估计为测量数据处理打开了一条广阔而深邃的研究天地,其成果已遍及大地测量、工程测量、航空摄影测量等学科[1]。最小二乘法最优性的前提是观测误差服从正态分布[2],文献[3]指出,当观测中的粗差率大于0.2%就有可能破坏最小二乘的平差效率。粗差为离群观测,具有偶然性和系统性双重特性。实际应用中粗差观测一般占数据总量的1~10%[3, 4]。
常用抗差估计方法有中位数法、最小p范数估计、抗差贝叶斯估计法和抗差最小二乘法、聚类分析法、拟准检定法等[5, 6, 7, 8, 9, 10, 11, 12]。一般而言,崩溃点越高的方法越稳健,在大样本情况下,中位数法的崩溃点可接近50%。优良稳健估计应与坐标系的选取无关,对于多维参数稳健估计而言,在每个坐标方向分别应用一维中位数法所得估计量不具有该性质[13]。多维中位数估计很大程度取决于对数据中位数的定义,文献[13]进行了较为全面的总结,并发展了基于最小方差-协方差矩阵体积的稳健估计法。自适应抗差最小二乘法和拟准检定法是我国大地测量学家丰富和发展的两种重要抗差估计方法[14, 15],如何利用当前小样本观测值快速获取可靠迭代初值或拟稳解,对抗差最小二乘法和拟准检定法均具有重要意义。一般而言,若该粗差观测值为杠杆观测,则该观测量的粗差很难被正确定位[16]。传统地,抗差估计需要首先获取稳健的参数初值(如中位数)[17],再利用该参数估值进行粗差探测和定位,上述过程循环往复、互相影响、互相制约。如何定位杠杆观测中的粗差是一个难点问题。
利用组合方法求解超定方程组最早见于高斯的日记。这种方法由雅克比独立公开发表[18],该方法建立了矛盾方程组的最小二乘解与方程组基础解的关系。对于线性平差模型,高斯-雅克比组合平差法等价于最小二乘平差[19, 20]。文献[21]将这种方法推广应用到测距定位方程平差,并推广至非线性一般问题。联合稳健估计中的M估计法,通过合理调整基础解的比重有望获取一簇稳健估计算子。
本文基于粗差的频率建立了粗差二项分布模型,探讨了超定方程组基础解粗差分群的性质;通过对基础解进行聚类分析,提取基础解的零粗差分群,进而提出了抗差高斯-雅克比组合平差法。
1 高斯-雅可比组合平差对于超定方程 Ax=L(L∈ n为观测向量,x∈
n为观测向量,x∈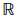 m为参数向量),其最小二乘解可表示为[19]:
m为参数向量),其最小二乘解可表示为[19]:
其中,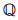 n,m={(i1,…,im)|1≤i1<…<im≤n,i∈
n,m={(i1,…,im)|1≤i1<…<im≤n,i∈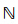 }为
}为 的m元递升指标集[23, 24],
的m元递升指标集[23, 24],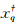 为超定方程组Ax=L的基础解:
为超定方程组Ax=L的基础解:
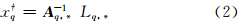
式中,Lq,*为观测向量L按递升指标集q索引所得子向量;Aq,*是由矩阵A的行向量按递升指标集q索引所得子矩阵。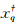 对
对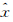 的权重为:
的权重为:
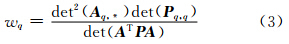
式中,P=diag(p1,p1,…,pn)为观测权阵。 由Binet-Cauchy定理易知[2]:

权因子wq与基础解的Werkmeister点位误差度量成反正。
2 污染分布与二项分布 2.1 观测污染分布在测量中,一般存在粗差出现的频率信息。设粗差概率为 q(定量分析时假定粗差概率q为0.05),服从正态分布φ(μ1,σ12),正常观测概率为1-q,服从正态分布φ(μ2,σ22),则观测污染分布为:
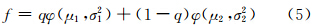
其期望为μ=qμ1+(1-q)μ2,方差为σ2=q [(μ1-μ)2+σ12]+(1-q)[(μ2-μ)2+σ22]。观测污染分布(5)可扩展为多个不同的概率分布,相关讨论可参考文献[25]。
2.2 粗差数目二项分布模型(5)是一种连续概率分布函数,用于刻划观测精度。对由n个观测量构成的样本空间,粗差数目z(0≤z≤n,z∈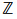 )为一随机变量,存在s个粗差的概率为:
)为一随机变量,存在s个粗差的概率为:
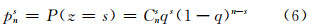
其中,Cns为在n个样本中选取s个样本的所有可能组合。显然,{pns}服从二项分布:
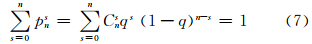
二项分布{pns}的数学期望为nq,其方差为nq(1-q),且当n→∞时,若q不趋近于0或1,{pns}趋近于正态分布。当n=20时,按概率出现大小,应逐次排查单粗差、双粗差、三粗差。
3 理论粗差分群及其概率当存在粗差时,粗差完全被基础解吸收,这使得基础解会明显偏离参数真值。
记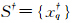 为基础解全集,
为基础解全集,
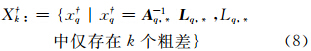
为基础解解集的粗差分群(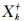 简称k粗差分群)。若n个观测中共存在s个粗差,则基础解全集可分解为:
简称k粗差分群)。若n个观测中共存在s个粗差,则基础解全集可分解为:

上述分解对应数字特征:
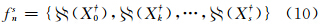
式中,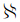 (
(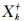 )表示k粗差分群
)表示k粗差分群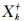 中基础解的数目。由k粗差分群的定义可知
中基础解的数目。由k粗差分群的定义可知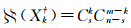 ,且
,且
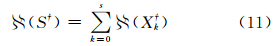
当参数维数m=3,观测数目小于等于5时,单粗差分群和零粗差分群不易分离;当6个观测量中存在1个粗差时,零粗差分群和单粗差分群数目相同,当存在2个粗差时,单粗差分群内基础解数目是零粗差分群的3倍。当零粗差分群中解的数目不占优势时,若不使用观测条件先验信息,则很难正确辨识零粗差分群。
类似地,也可以按非粗差观测对基础解解集进行分类,即粗差分群的数字特征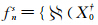 ,
,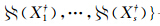 一一对应以下数字特征:
一一对应以下数字特征:
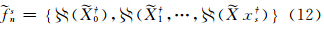
其中,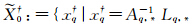 ,Lq,*中仅存在k个正常观测},且
,Lq,*中仅存在k个正常观测},且

由式(13)可得,给定的数字特征{n0,n1,…,ns}对应s个粗差和n-s个粗差两个事件,即
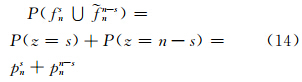
结合式(6),可得:
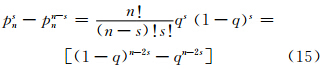
且仅当q<0.5,s≤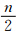 时存在
时存在

可见,任意数字特征{n0,n1,…,ns}对应存在s个粗差和n-s个粗差两个事件,若q<0.5,则粗差数z≤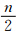 的概率更大,否则粗差数z≥
的概率更大,否则粗差数z≥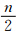 的概率更大。若q<0.5,应将元素数目大的分群作为零粗差分群,这符合粗差的离群性质;而q>0.5,应将元素数目小的分群作为零粗差分群,这显然不符合粗差的离群性质。
的概率更大。若q<0.5,应将元素数目大的分群作为零粗差分群,这符合粗差的离群性质;而q>0.5,应将元素数目小的分群作为零粗差分群,这显然不符合粗差的离群性质。
聚类分析是对集合元素的一种分类方法,元素与元素的相似程度由距离函数定义。本文以最短距离法为例介绍对基础解解集进行聚类分析的方法。分群Xi与Xj间的距离可定义为两个分群中基础解间最小距离,即
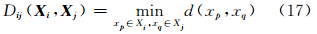
若将分群Xi与分群Xj合并为Xr,则任意分群Xk到Xr的距离可由式(17)导出:
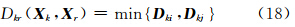
将每个基础解视为独立分群,计算基础解间的距离,并将距离矩阵记为D(0),搜索D(0)的非对角线最小元素,设为Dij,则将分群Xi和分群Xj合并为Xr,即Xr=Xi∪Xj。将D(0)中第i、j行及i、j列合并,所得到的矩阵记为D(1)。按式(18)计算合并分群Xr与其它分群的距离,由D(1)重复上述过程得D(2)。依次类推,直到所有的基础解并成一个分群为止。
由粗差二项分布模型计算特定粗差数出现的概率。根据相应粗差分群数字特征对基础解聚类分析结果进行分群处理,计算各分群方差,由准则式(20)所确定的分群视为基础解零粗差分群的估计,并记为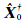 ,则可得到抗差高斯-雅可比组合平差公式:
,则可得到抗差高斯-雅可比组合平差公式:
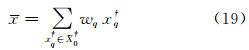
式中,零粗差分群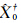 满足
满足
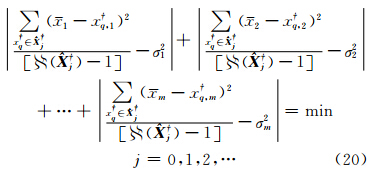
式中,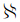 (
( )为第j个分群
)为第j个分群 中基础解的数目;
中基础解的数目;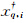 表示基础解
表示基础解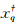 的第i个参数;σi2为第i个参数
的第i个参数;σi2为第i个参数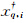 的先验方差。
的先验方差。
基于基础解聚类分析的高斯-雅可比抗差估计与坐标系选取无关,这符合优良稳健估计方法的特性[13]。零粗差分群的均值也是稳健的,但平差效率会低于式(19)。
5 算例分析算例采用Trimble 4700双频接收机实测观测数据(采样间隔15 s,共计162个观测历元),进行逐历元伪距单点定位。
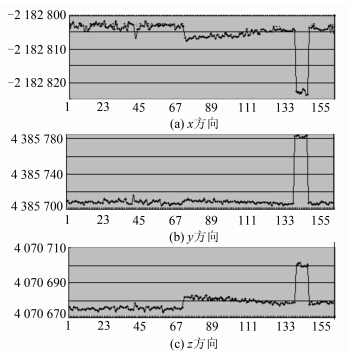
定位结果(图 1)表明,第139至146历元伪距单点定位结果发生了跳变。下面分别使用最小二乘法、抗差最小二乘法和抗差高斯-雅克比组合平差法探测第139个历元中的粗差。
|
| 图 1 逐历元定位 Fig. 1 Positioning Epoch by Epoch |
利用高斯-牛顿迭代法对第139个历元进行非线性最小二乘估计,可得最小二乘估计:
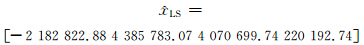
单位权方差的估值为:
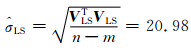
通过考察最小二乘残差很难发现存在粗差。
5.2 抗差最小二乘估计采用文献[17]给出的方法,在每个坐标方向分别应用一维中位数法,可探测出7号卫星(第3个观测量)伪距存在粗差,将其剔除后可得最小二乘估计为:

单位权方差的估值为:
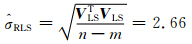
可见,抗差最小二乘通过定位和剔除粗差,提高了定位解的可靠性。
5.3 抗差高斯-雅克比组合法设粗差概率为q=0.05,根据式(6),8个观测量中存在1个粗差的概率为0.279 33。抗差高斯-雅克比平差的步骤如下。
1) 聚类分析。计算70个基础解的聚类谱。
2) 提取基础解零粗差分群。点位密度较大分群作为第一分群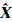 0,包含30个基础解,剩余40个基础解作为第二个分群
0,包含30个基础解,剩余40个基础解作为第二个分群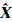 1(当有8个观测、4个待估参数、1个粗差时,存在两个分群,粗差分群理论数字特征为f81= 35,35,0,…0 )。
1(当有8个观测、4个待估参数、1个粗差时,存在两个分群,粗差分群理论数字特征为f81= 35,35,0,…0 )。
3) 抗差高斯-雅克比组合平差。计算分群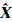 0和
0和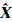 1中基础解在各个方向的离散概率密度函数的方差,可得分群
1中基础解在各个方向的离散概率密度函数的方差,可得分群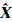 0最接近先验点位精度信息。将
0最接近先验点位精度信息。将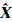 0作为零粗差分群,有:
0作为零粗差分群,有:
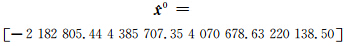
且
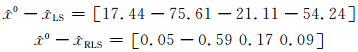
不难发现,抗差高斯-雅克比组合平差法是稳健、高效的。
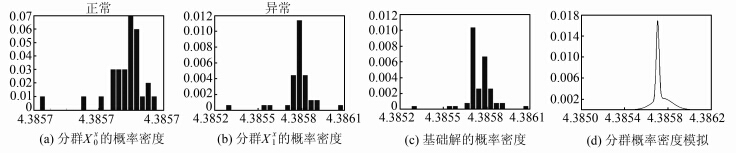
为进一步验证本文的结论,图 2给出了基础解在y坐标方向上的离散概率密度分布,其中,图 2(a)、2(b)为零粗差分群估计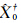 和单粗差分群估计
和单粗差分群估计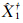 的 概率密度图,图 2(c)为所有基础解的概率密度图,图 2(d)则是由图 2(a)、2(b)概率密度拟合正态分布后按式(1)计算所得的混合连续概率密度。
的 概率密度图,图 2(c)为所有基础解的概率密度图,图 2(d)则是由图 2(a)、2(b)概率密度拟合正态分布后按式(1)计算所得的混合连续概率密度。
|
| 图 2 基础解及分群分布(y方向) Fig. 2 Probability Density of Clustering(y Coordinate) |
类似地,考察其他方向基础解的概率分布。粗差对x、z方向主要表现为混合后的概率分布出现方差膨胀现象,而在y方向既存在方差膨胀,又存在均值漂移现象,导致整体基础解出现两个峰值。这也是中位数估计在y方向与抗差最小二乘解存在 30 m偏差的重要原因。
6 结 语1) 粗差出现的概率信息可用于建立观测污染分布模型和粗差数目二项分布模型,可用于数据处理前的先验分布建模和后验分布模拟。
2) 通过对基础解解集进行聚类分群,提取零粗差分群,可实现抗差高斯-雅可比组合平差。
3) 理论上,抗差高斯-雅可比组合平差法的平差效率等价于抗差最小二乘平差法,实际平差效率则取决于零粗差分群的分离程度。
4) 抗差高斯-雅可比组合平差法的实质是在样本中提取与先验观测条件最为接近的子样本,无需稳健参数初值和迭代计算,在一定程度上解决了杠杆观测中的粗差定位问题。
5) 当观测自由度很大时,高斯雅克比组合的计算复杂性较高,此时可将超定方程组进行分组处理。
| [1] | Yang Yuanxi.Lecture Series About Robust Theory of Least Squares Estimation-Basic Concepts and Main Task[J].Bulletin of Surveying and Mapping, 1994(4):36-39(杨元喜.测量抗差最小二乘估计理论系列讲座(一)--抗差估计的概念及其任务[J].测绘通报,1994(4):36-39) |
| [2] | Zhou Jiangwen.Theory of Errors[M].Beijing:Surveying and Mapping Press,1981(周江文.误差理论[M].北京:测绘出版社,1981) |
| [3] | Huber P J.Robust Statistics,Wiley Series in Probability and Mathematical Statistics[M].New York:Wiley,1981 |
| [4] | Li Guochong,Xia Yunqing,Jiao Huiping.Distribution of Outliers and the Random Number Generation[J].Journal of Zhongzhou University,2010,27(5):111-113(李国重,夏云青,焦慧平.粗差分布及其随机数产生[J].中州大学学报,2010,27(5):111-113) |
| [5] | Zhou Jiangwen.Classical Theory of Error and Robust Estimatiion[J].Acta Geodaetica et Cartographica Sinica, 1989,18(2):115-120(周江文.经典误差理论与抗差估计[J].测绘学报,1989,18(2):115-120) |
| [6] | Zhou Jiangwen,Huang Youcai,Yang Yuanxi,et al.Robust Least Squares Method[M].Wuhan:Press of Huazhong University of Science and Technology,1997(周江文,黄幼才,杨元喜,等.抗差最小二乘法[J].武汉:华中理工大学出版社,1997) |
| [7] | Yang Yuanxi.Adaptively Robust Least Squares Estimation[J].Acta Geodaetica et Cartographica Sinica, 1996,25(3):206-211(杨元喜.自适应抗差最小二乘估计[J].测绘学报,1996,25(3):206-211) |
| [8] | Yang Yuanxi.Robust Bayesian Estimation[J].Bulletin Géodésique,1991,65(3):145-150 |
| [9] | Rousseeuw P J.Least Median of Squares Regression[J].Journal of the American Statistical Association,1984,79(14):871-880 |
| [10] | Rousseeuw P J,Driessen K V.A Fast Algorithm for the Minimum Covariance Determinant Estimator.Technometrics,1999,41(3):212-223 |
| [11] | Kaufman L,Rousseeuw P J.Finding Groups in Data:an Introduction to Cluster Analysis.Wiley Series in Probability and Mathematical Statistics Applied Probability and Statistics.1990,New York:Wiley.xiv,342 |
| [12] | Shi Fusheng.Gross Error Detection by Cluster Analysis[J].Journal of the Plainstitute of Surveying and Mapping,1989(2):66-71(时富生.用聚类分析法进行粗差定位[J].测绘学院学报,1989(2):66-71) |
| [13] | Rousseeuw P J,Leroy A M.Robust Regression and Outlier Detection.Wiley Series in Probability and Mathematical Statistics Applied Probability and Statistics,New York:Wiley,1987 |
| [14] | Ou Jikun.Quasi-Accurate Detection of Gross Errors (QUAD)[J].Acta Geodaetica et Cartographica Sinica,1999,28(1):15-19(欧吉坤.粗差的拟准检定法(QUAD法)[J].测绘学报,1999,28(1):15-19) |
| [15] | Ou Jikun.A New Method to Gross Errors Detectio-Quasi-Accurate Detection[J].Chinese Science Bulletin,1998,44(8):1 777-1 779(欧吉坤.一种检测粗差的新方法--拟准检定法[J].科学通报,1998,8(44):1 777-1 779) |
| [16] | Jiangwen Z,Yuanxi Y.On Residuals and Leverage Observations[C].In:Zhou Jiangwen,Yang Yuanxi,Ou Jikun,et al.Proceedings on Robust Estimation.Beijing:Surveying and Mapping Press,1992 |
| [17] | Yang Ling,Shen Yunzhong,Lou Lizhi.Equiva lent Weight Robust Estimation Method Based on Median Pa rameter Estimates[J].Acta Geodaetica et Cartographica Sinica,2011,40(1):28-32(杨玲,沈云中,楼立志.基于中位参数初值的等价权抗差估计方法[J].测绘学报,2011,40(1):28-32) |
| [18] | Awange J L.Springer Link (Online service),Algebraic geodesy and geoinformatics[J].Heidelberg:Springer,2010 |
| [19] | Ben-Tal A,Teboulle M.A Geometric Property of the Least Squares Solution of Linear Equations[J].Linear Algebra and its Applications, 1990,139:165-170 |
| [20] | Miao J,Ben-Israel A.The Geometry of Basic,Approximate,and Minimum-norm Solutions of Linear Equations[J].Linear Algebra and its Applications,1995,216:25-41 |
| [21] | Awange J L,Grafarend E W.Explicit Solution of the Overdetermined Three-dimensional Resection Problem[J].Journal of Geodesy,2003,76(11/12):605-616 |
| [22] | Jacobi C.Deformatione et Proprietatibus Determinantum[R].Crelle's Journal fur die reine und angewandte Mathematik,Bd.22,1841 |
| [23] | Ben-Israel A.A Volume Associated with m×n matrices[J].Linear Algebra and its Applications,1992,167:87-111 |
| [24] | Xue Shuqiang,Dang Yamin,Chen Wu.Matrix Volume Method of the Mean Square Deviation Computation of Least Square Solution[J].Geomatics and Information Science of Wuhan University,2009,34(9):1 106-1 109(薛树强,党亚民,陈武.最小二乘估值均方差计算的矩阵体积法[J].武汉大学学报·信息科学版,2009,34(9):1 106-1 109) |
| [25] | Ray S,Lindsay B G.The Topography of Multivariate Normal Mixtures[J].The Annals of Statistics,2005,33(5):2 042-2 065 |
 2015, Vol. 40
2015, Vol. 40



