文章信息
- 卢辰龙, 匡翠林, 易重海, 章浙涛
- LU Chenlong, Kuang Cuilin, YI Zhonghai, ZHANG Zhetao
- 奇异谱分析滤波法在消除GPS多路径中的应用
- Singular Spectrum Analysis Filter Method for Mitigation of GPS Multipath Error
- 武汉大学学报·信息科学版, 2015, 40(7): 924-931
- Geomatics and Information Science of Wuhan University, 2015, 40(7): 924-931
- http://dx.doi.org/10.13203/j.whugis20130570
-
文章历史
- 收稿日期:2013-09-19
2. 国土环境与灾害监测国家测绘地理信息局重点实验室, 江苏 徐州, 221006
2. NASG Key Laboratory of Land Environment and Disaster Monitoring, Xuzhou 221006, China
在GPS变形监测中,由于基线一般较短,可以通过差分技术消除或减弱电离层延迟、对流层延迟、卫星轨道误差、接收机和卫星钟差等与基线长度无关的误差项,但多路径效应在基线两端不具有相关性,无法通过差分消除,因此,多路径效应误差成为GPS短基线差分测量的主要误差来源[1]。目前,处理多路径效应误差的方法可以分为天线设计、接收机信号处理以及数据后处理等3类。在动态变形监测中,由于测站一般固定且周围环境基本保持不变,可以根据多路径效应周日重复性的特点,采用各种滤波方法[2, 3, 4, 5, 6]对其建模,从而削弱多路径效应的影响。
奇异谱分析(singular spectrum analysis,SSA)[7]是在Karhumen-Loeve分解理论的基础上发展起来的,是对一维的时间序列进行分析的主成分分析方法[8]。SSA从时间序列的动力重构出发,并与经验正交函数相联系,可以较好地从短噪声时间序列中提取信息。由于SSA不受正弦波假定的约束、无需先验信息、具有稳定识别和强化周期信号的优点,近年来已成功应用于大地测量领域[9, 10, 11]。但SSA过程中嵌入维数L和重构阶次P这两个参数的选择仍然没有一个较为明确的标准[12],大部分都是主观选择的。确定重构阶次P有不同的方法,如Figueiredo[13]与Ma[14]采用设定阈值确定重构阶次P,即选择前几个特征值,其贡献率之和要满足设定的阈值;Hu[15]通过奇异谱对数图的第一个拐点处(含拐点)的特征值个数来确定重构阶次P,但这两种方法都存在局限性,同时也未考虑嵌入维数L对去噪的影响。本文根据噪声与信号的Hurst指数有显著差异这一特性建立了一种基于SSA的滤波方法,同时给出了SSA的嵌入维数L与重构阶次P的确定标准;然后对不同噪声水平的模拟数据及实际GPS数据进行了实验分析,验证了SSA滤波的有效性。
1 SSA滤波法 1.1 SSA方法对于一维时间序列x=(x1,x2,x3,…,xN),其中N>2,且x是非零向量,即至少存在一个xi≠0,其SSA[16, 17]过程主要分为以下4个步骤。
1)计算轨迹矩阵X。
将给定的时间序列根据需要嵌入维数L,K=N-L+1,(1<L≤N/2),组建一个L×K阶的轨迹矩阵X:
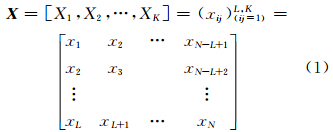
式中,Xi=(xi,xi+1,…,xi+L-1),轨迹矩阵X的(i,j)处的元素xij=xi+j-1即所有反对角线上的元素相等。
2)奇异值分解(singular value decomposition,SVD)
定义矩阵CX=XXT,XT为X的转置矩阵,求出CX的特征值λi与特征向量Ui,并将特征值按照降序进行排列,特征值依次为λ1,…,λL且λ1≥…≥λL≥0,对应的特征向量为U1,…,UL。设d=L*,L*=min{L,K},Vi=XTUi/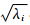 ,(i=1,…,d),Ui与Vi是轨迹矩阵的左右特征向量,因此,SVD分解的轨迹矩阵X可由初等矩阵合成:
,(i=1,…,d),Ui与Vi是轨迹矩阵的左右特征向量,因此,SVD分解的轨迹矩阵X可由初等矩阵合成:
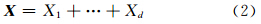
式中,初等矩阵为Xi=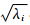 UiViT,rank(Xi)=1,
UiViT,rank(Xi)=1,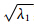 ≥…≥
≥…≥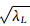 ≥0称为序列X的奇异谱,其最大特征值对应最大的特征向量,代表了信号的最大变化趋势,而较小特征值对应的特征向量代表了信号的噪声。
≥0称为序列X的奇异谱,其最大特征值对应最大的特征向量,代表了信号的最大变化趋势,而较小特征值对应的特征向量代表了信号的噪声。
3)分组
将初等矩阵Xi的下标{1,2,…,d}分成p个不相交的子集I1,I2,…,Ip,设I={i1,i2,…,im},那么合成矩阵XI=Xi1+Xi2+…+Xim,计算集合I=I1,…,Ip的每个合成矩阵,那么式(2)的分解式可写为:
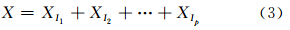
其中,选取集合I1,…,Ip的过程称为分组。
4)对角平均
将式(3)分组分解的每个矩阵XIj转换为长度为N的新序列,设Y是一个L×K的矩阵,其元素为yij,其中1≤i≤L1≤j≤K,K*=max{L,K},L*=min{L,K}且N=L+K-1,使用对角平均公式将矩阵Y转换为y1,…,yN的时间序列,其公式为:
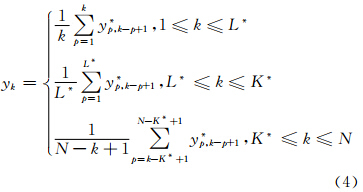
将式(4)用在合成的矩阵XIk中,生成一个重构的序列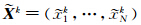 ,因此,初始的时间序列x1,…,xN分解为总和为p的重构序列:
,因此,初始的时间序列x1,…,xN分解为总和为p的重构序列:
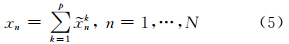
Hurst指数是Hurst在20世纪中叶提出的一种判别时间序列是否对时间有依赖的参数,经过几十年的研究,Hurst指数已在时间序列数据分析中得到了普遍的应用,但主要用于对经济数据和自然灾害数据的分析。Hurst指数可以描述高斯噪声分形特性,当H=0.5时,表示的是布朗运动(白噪声);当H<0.5时,是高斯变量过程;当H>0.5时,是长期记忆相关的过程,一般将H≤0.5的时间序列数据当作噪声[18]。目前,Hurst指数的估值方法主要有绝对值法、聚合方差法、R/S分析法、周期图法、Whittle法和小波分析法等[19]。小波分析法被认为具有较高精度,但算法较复杂,R/S法应用得最普遍,但其并未考虑趋势或周期的影响,且受数据长度的限制,使得结果的可靠性会受到一定程度的影响,而聚合方差法受数据长度及趋势或周期影响较小[20]。因此,本文选用的是聚合方差法。聚合方差法的基本原理如下[21]:
首先,对于给定的时间序列Xi,i=1,2,…,N,根据长度为m,将时间序列Xi,i=1,2,…,N分割成[N/m]=k个子区间,并计算每个子区间的平均值Xm(k),然后计算子区间平均值的方差Var(Xm),最后,采用最小二拟合双对数图上(m,Var(Xm))的斜率α,Hurst指数为H=(α/2)+1。
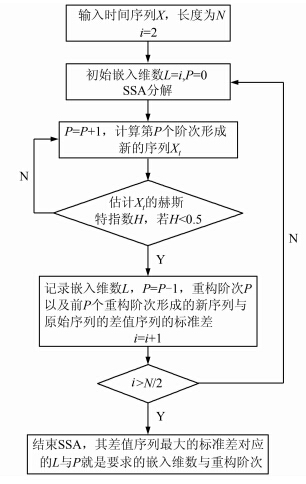
1.3 SSA滤波法对于SSA,若嵌入维数L太大,则会导致奇异值分解得到不同的部分产生混叠,L太小,无法使信号从弱到强渐进划分,从而使得部分信号无法获取,因此嵌入维数L的选择对于SSA是十分重要。但SSA的嵌入维数L基本上是主观选择的,并没有一个统一的标准,尤其是处理不同类型的数据时,其选择也是不同的。而重构阶次P表示这前P个分量是信号,若P太小,则表示后面部分信号被当作噪声剔除掉,P太大,则会使得部分噪声被当作信号而提取出来。本文提出的SSA滤波法的核心思想如下:①先进行内循环,利用信号与噪声的时间序列Hurst指数差异较大,在给定嵌入维数L的情况下,令重构阶次P=1,计算重构后的时间序列的Hurst指数H,若H>0.5,则令P=P+1,重复上述过程,直到第P个阶次得到重构时间序列的Hurst指数H≤0.5,此时其重构阶次P=P-1,并计算重构后时间序列与原始时间序列的差值序列的标准差;②进行外循环,对不同的嵌入维数L重复内循环的过程;③根据上述内循环与外循环,确定差值序列中最大的标准差,与其对应的嵌入维数L与重构阶次P就是要求的值。其具体步骤如图 1所示。
|
| 图 1 SSA滤波法流程图 Fig. 1 Schematic of the SSA Filter Method |
为了验证本文提出SSA滤波法的有效性与优越性,模拟了一组数据并分别加入了6组不同大小的噪声,模拟数据模型为:

式中,yt是由ut与et两部分构成,其中ut由1 200 s、700 s、和300 s的3种谐波信号构成,即ut=sin(2πt/1 200)+sin(2πt/700)+sin(2πt/300)et表示噪声,服从正态分布,6组噪声分别为N(0,0.52)、N(0,12)、N(0,1.52)、N(0,22)、N(0,2.52)与N(0,32),模拟数据的样本数为3 000,采样间隔为1 s。为了进一步验证该方法的稳健性,又与小波滤波与(empirical,mode decomposition,EMD)去噪法进行了比较,其中,采用的小波为信号处理常用的db8小波,分解层数定为2~8,采用软阈值处理,通过最大相关性来选取最佳分解层次,EMD滤波去噪标准参考文献[2]。同时又将本文提出的SSA滤波法与其他的SSA滤波方法进行比较,验证了本文算法的优越性。
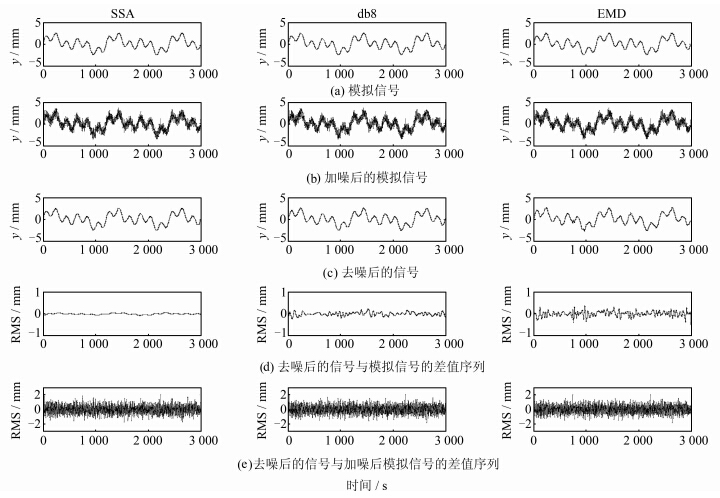
2.1 与小波与EMD方法的对比为确保能准确地评判本文提出方法的去噪效果,选用了文献[2]给出的3种常用的评价指标,分别为滤波后噪声部分的NRMS值、滤波后信号部分的SRMS值以及去噪后的信号与原始信号的相关系数R。图 2为随机噪声et服从N(0,0.52)时3种滤波方法的模拟实验结果。通过对比可以看出,图中SSA滤波法相对于db8小波与EMD去噪法的消噪后信号序列与模拟信号序列的差值序列整体比较平稳趋近于零,且这3种方法去噪后信号与加噪后模拟信号的差值序列整体相似,保持一致,说明SSA滤波法可以有效地提取信号,具有良好的去噪能力。
|
| 图 2 3种滤波方法的模拟实验结果 Fig. 2 Simulation Results of Three Kinds of Filtering Method |
表 1、表 2与表 3分别为6种噪声水平下SSA滤波法、db8小波与EMD去噪法的实验结果。从滤波后噪声部分的NRMS值可以看出,3种方法的NRMS值大小基本相当。随着加入噪声增大,采用3种方法分别滤波后信号部分的SRMS值也随着增大,但SSA滤波法相对较小,这说明SSA滤波法提取信号的性能要优于db8小波与EMD去噪法,且其提出得到的信号与真实的信号最为接近。另外,3种方法的相关系数随着噪声的增大而逐渐减小,但SSA滤波法的相关系数R值最小为0.98,而db8小波与EMD去噪法的相关系数R值分别为0.95与0.92。综合与小波与EMD方法的各项指标对比,验证了本文提出SSA滤波法的有效性。
| 噪声水平 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| NRMS/mm | 0.50 | 0.99 | 1.47 | 1.99 | 2.44 | 2.99 |
| SRMS/mm | 0.03 | 0.07 | 0.11 | 0.11 | 0.19 | 0.25 |
| R | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.98 |
| 噪声水平 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| NRMS/mm | 0.49 | 1.0 | 1.46 | 1.99 | 2.44 | 2.98 |
| SRMS/mm | 0.08 | 0.15 | 0.19 | 0.22 | 0.28 | 0.38 |
| R | 1.00 | 0.99 | 0.99 | 0.98 | 0.97 | 0.95 |
| 噪声水平 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| NRMS/mm | 0.49 | 1.0 | 1.46 | 1.99 | 2.44 | 2.97 |
| SRMS/mm | 0.12 | 0.24 | 0.22 | 0.32 | 0.39 | 0.49 |
| R | 1.00 | 0.98 | 0.98 | 0.97 | 0.95 | 0.92 |
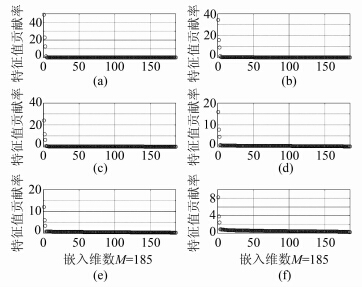
为了验证本文提出的SSA滤波法的优越性,将本文提出的方法与其他SSA滤波方法进行了比较。设定阈值法确定重构阶次P类似于主成分分析法,该方法只适用于信噪比较高的数据,对于实际数据未知信噪比时,影响较大,如图 3所示。
|
| 图 3 不同噪声背景下各个特征值的方差贡献率 Fig. 3 The Variance Contribution of Eigenvalues Under Different Noise Background |
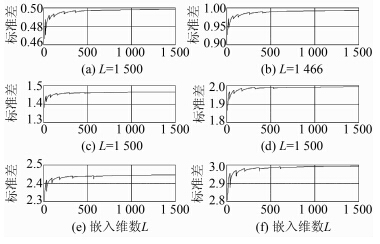
从图 3中各子图中可以看出在上述不同噪声背景下,前P个重构阶次特征值方差贡献之和并不一致,因此,在实际数据处理中,未知数据的先验信息时,该方法并不适用;而通过奇异谱对数图的第一个拐点确定重构阶次P的方法在模拟数据中有较好的去噪效果,但在多路径数据中并不适用,下文的多路径数据实验对该情形进行了详细分析。上述两种方法确定重构阶次P都存在着缺陷,且都未考虑不同的嵌入维数L对去噪的影响,而嵌入维数L又影响SSA滤波去噪的结果,如图 4所示。图 4中各子图分别是在上述6种噪声水平下,不同嵌入维数L重构后的时间序列与原始时间序列差值的标准差序列,其标题L值表示的是标准差最大值对应的嵌入维数,可以看出,嵌入维数L较小时,其标准差变化较大,随着L的增大,其标准差逐渐趋于稳定且越来越接近加入噪声的标准差,因此,在处理实际数据去噪时,应该考虑嵌入维数L的影响。综合上述对仿真数据的分析表明,本文提出的基于噪声与信号的Hurst指数有显著差异这一特性建立的SSA滤波法是一种有效的去噪方法。
|
| 图 4 不同嵌入维数L的标准差序列 Fig. 4 The Standard Deviation Series of Different Embedding Dimension L |
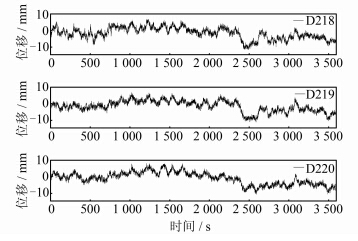
在某教学楼放置两台GPS接收机进行实验,观测环境有多处产生多路径信号的强反射面,采用Topcon双频接收机,天线类型为Topcon CR3扼流圈天线,流动站使用Septentrio接收机和普通测地型天线,采样间隔为1 s,从2006年年积日218日~220日连续3 d,每天观测时间为1h。由于基线非常短,接收机钟差和卫星钟差被消除,电离层、对流层误差被极大地削弱,其残差可以忽略不计。因此,实际GPS测量得到的位移序列中仅包含随机噪声和多路径误差。X方向的原始坐标时间序列对齐后,如图 5所示。
|
| 图 5 连续3天X方向的原始坐标序列 Fig. 5 Raw Coordinates of X Direction for the Three Consecutive |
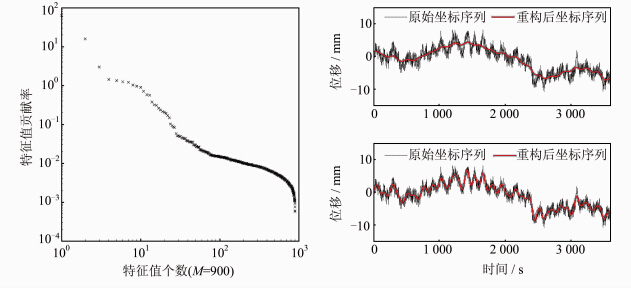
从图 5可以看出,位移序列表现出明显的周日重复性。当周围环境不变或者变化很小,多路 径效应误差可利用其周日重复性进行改正,即根据多路径重复性的特点,首先对三天的原始坐标时间序列进行滤波去噪,并提取精确的多路径误差模型,然后用第一天获得的多路径模型与后续两天提取的多路径模型相减,从而消除多路径效应,提高GPS坐标序列的定位精度。图 6(a)、6(b)与6(c)分别是GPS坐标时间序列的奇异谱对数图、根据拐点确定重构分量的重构坐标序列图以及本文算法的重构坐标序列图,从图中可以看出,其奇异谱图第一个明显的拐点确定了前4个特征值对应的分量作为重构分量,但重构后的多路径序列信号显然被过度剔除了,证明了奇异谱对数图确定重构阶次P的方法并不适用,而本文采用Hurst指数估计每个重构分量,可以准确的确定重构阶次P,验证了该算法的优越性。
|
| 图 6 特征值对数图及重构多路径坐标序列 Fig. 6 The Eigenvalue Logarithmic Diagrams and The Reconstruction of Multipath Coordinate Series |
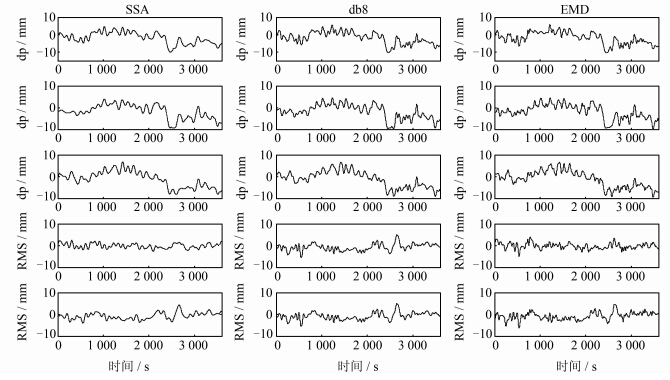
图 7是SSA、小波、EMD滤波消噪的结果,图中前3行的子图分别为3种滤波方法提取连续3 d的多路径模型序列,后两行子图为第2天和第3天与第1天的多路径模型差值序列。通过对比可以看出,SSA方法提取的多路径模型差值序列与db8小波结果相当,但其稳定度要优于小波方法,以上两种方法都要优于EMD去噪法。又分别将滤波前后坐标序列的RMS值、经多路径模型改正后坐标序列的RMS值以及坐标序列间的相关系数作为滤波质量以及多路径重复性的评价准则,对其进行比较分析,3种方法的比较分析结果分别列于表 4~表 6中。从表 4的结果可以看出,SSA方法滤波后的RMS值与其他两种方法的效果基本一致,但与滤波前的RMS值相差不大,说明随机噪声只占很小的一部分,多路径效应占主导地位。表 5的结果则表明前后两天的GPS多路径效应具有很强的重复性,SSA方法与db8小波提取具有重复性的GPS多路径效应的效果基本相当,但都比EMD去噪法效果要好。表 6的结果则进一步表明,SSA方法能够得到精确的多路径改正模型。
|
| 图 7 3种方法的滤波结果 Fig. 7 Result After De-Noising Using the Three Kinds of Method |
| 时间 | 滤波前 | SSA | EMD | db8 |
| D218 | 3.58 | 3.25 | 3.36 | 3.37 |
| D219 | 3.43 | 3.18 | 3.25 | 3.25 |
| D220 | 3.83 | 3.65 | 3.70 | 3.68 |
| 时间 | 滤波前 | SSA | EMD | db8 |
| D218~D219 | 0.86 | 0.94 | 0.92 | 0.94 |
| D219~D220 | 0.84 | 0.91 | 0.90 | 0.91 |
| D218~D220 | 0.81 | 0.91 | 0.89 | 0.90 |
| 时间 | 滤波前 | SSA | EMD | db8 |
| D219 | 3.43 | 1.10 | 1.32 | 1.16 |
| D220 | 3.83 | 1.54 | 1.71 | 1.64 |
SSA是一种对信号的识别和描述采用时域性的频域特征分析方法,基于此,本文提出了一种利用噪声与信号的Hurst指数具有显著差异的特性建立的SSA滤波法。将本文提出的SSA滤波法与其他学者提出的SSA滤波法以及小波滤波和EMD方法进行了对比,得出以下结论:① 通过模拟不同噪声水平的数据,验证了本文提出的SSA滤波有效性,并通过对比分析,得出了SSA滤波法的去噪效果与小波方法和EMD方法相当;② 嵌入维数L的选取影响SSA去噪的性能,在去噪时应当尽量选取较大的嵌入维数;③ 确定了嵌入维数L与重构阶次P的选择标准,避免了这两个参数选择的盲目性与主观性,验证了本文提出的确定重构阶次P的方法优于其他方法。④ 将该方法用于提取多路径误差重复模型,利用该模型对多路径进行改正,可有效地削减多路径效应的影响,提高GPS的定位精度。尽管本文提出的SSA滤波法可以确定出嵌入维数L与重构阶次P,但计算时间较长,如何提高其计算效率还需进一步研究。
| [1] | Dai Wujiao,Ding Xiaoli,Zhu Jianjun.Study on Multipath Effect in Structure Health Monitoring using GPS[J].Journal of Geodesy and Geodynamics,2008,28(1):65-71(戴吾蛟,丁晓利,朱建军.GPS动态变形测量中的多路径效应特征研究[J].大地测量与地球动力学,2008,28(1):65-71) |
| [2] | Dai Wujiao,Ding Xiaoli,Zhu Jianjun,et al.EMD Filter Method and Its Application in GPS Multipath[J].Acta Geodaetica et Cartographica Sinica,2006,35(4):321-327(戴吾蛟,丁晓利,朱建军,等.基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用[J].测绘学报,2006,35(4):321-327) |
| [3] | Zhang Haonan,Kuang Cuilin,Lu Chenlong,et al.A Multipath Correction Method Based on Wavelet Filtering and PCA[J].Journal of Geodesy and Geodynamics,2013,33(4):137-141(张昊楠,匡翠林,卢辰龙,等.基于小波滤波和PCA组合的多路径改正方法[J].大地测量与地球动力学,2013,33(4):137-141) |
| [4] | Luo Feixue,Dai Wujiao,Wu Xixiu.EMD Filtering Based on Cross-Validation and Its Application in GPS Multipath[J].Geomatics and Information Science of Wuhan University,2012,37(4):450-453(罗飞雪,戴吾蛟,伍锡锈.基于交叉证认的EMD滤波及其在GPS多路径效应中的应用[J].武汉大学学报·信息科学版,2012,37(4):450-453) |
| [5] | Zhong Ping,Ding Xiaoli,Zheng Dawei,et al.Separation of Structural Vibrations and GPS Multipath Signals Using Vondrak Filter[J].Journal of Central South University (Science and Technology),2006,37(6):1 189-1 195(钟萍,丁晓利,郑大伟,等.Vondrak滤波法用于结构振动与GPS多路径信号的分离[J].中南大学学报·自然科学版,2006,37(6):1 189-1 195) |
| [6] | Lu Chenlong,Kuang Cuilin,Zhang Haonan,et al.Multipath Correction Method by Combining EMD and PCA[J].Geotechnical Investigation&Surveying,2014(5):58-62(卢辰龙,匡翠林,张昊楠等.组合EMD和PCA的多路径改正方法[J].工程勘察,2014(5):58-62) |
| [7] | Vautard R,Yiou P,Ghil M.Singular-spectrum Analysis:A Toolkit for Short,Noisy Chaotic Signals[J].Physica D:Nonlinear Phenomena,1992,58(1):95-126 |
| [8] | Xu Kehong,Cheng Pengfei,Wen Hanjiang.Singular Spectrum Analysis and Wavelet Analysis on the Series of Sunspot[J].Science of Surveying and Mapping,2007,32(6):35-38(徐克红,程鹏飞,文汉江.太阳黑子数时间序列的奇异谱分析和小波分析[J].测绘科学,2007,32(6):35-38) |
| [9] | Chen Q,van Dam T,Sneeuw N,et al.Singular Spectrum Analysis for Modeling Seasonal Signals from GPS Time Series[J].Journal of Geodynamics,2013,72:25-35 |
| [10] | Rangelova E,Sideris M G,Kim J W.On the Capabilities of the Multi-channel Singular Spectrum Method for Extracting the Main Periodic and Non-periodic Variability from Weekly GRACE Data[J].Journal of Geodynamics,2012,54:64-78 |
| [11] | Wang Jiexian,Lian Lizhen,Shen Yunzhong.Application of Singular Spectrum Analysis to GPS Station Coordinate Monitoring Series[J].Journal of TongJi University (Natural Science),2013,(2):282-288(王解先,连丽珍,沈云中.奇异谱分析在GPS站坐标监测序列分析中的应用[J].同济大学学报·自然科学版,2013(2):282-288) |
| [12] | Golyandina N,Zhigljavsky A.Singular Spectrum Analysis for Time Series[M].N Y:Springer-Verlag,2013 |
| [13] | Figueiredo M B,de Almeida A,Ribeiro B.Wavelet Decomposition and Singular Spectrum Analysis for Electrical Signal Denoising[C].Systems,Man,and Cybernetics (SMC),International Conference on IEEE,Biopolis,Singapore,2011 |
| [14] | Ma J,Li Z T,Wang B B.Application of Singular Spectrum Analysis to the Noise Reduction of Intrusion Detection Alarms[J].Journal of Computers,2011,6(8):1 715-1 722 |
| [15] | Hu B,Li Q,Smith A.Noise Reduction of Hyperspectral Data Using Singular Spectral Analysis[J].International Journal of Remote Sensing,2009,30(9):2 277-2 296 |
| [16] | Alonso F J,Castillo J M D,Pintado P.Application of Singular Spectrum Analysis to the Smoothing Of Raw Kinematic Signals[J].Journal of biomechanics,2005,38(5):1 085-1 092 |
| [17] | Jiang Zhihong,Ding Yuguo.Generality and Applied Featrues for Singular Spectrum Analysis[J].Acta Meteorologica Sinica,1998,56(6):736-745(江志红,丁裕国.奇异谱分析的广义性及其应用特色[J].气象学报,1998,56(6):736-745) |
| [18] | Montillet J P,Tregoning P,McClusky S,et al.Extracting White Noise Statistics in GPS Coordinate Time Series[J].IEEE Geoscience and Remote Sensing Letters,2012,10(3):563-567 |
| [19] | Rea W,Oxley L,Reale M,et al.Estimators for Long Range Dependence:An Empirical Study[J].Electronic Journal of Statistics,2009,30:1-16 |
| [20] | Jiang Tianhan,Deng Liantang.Some Problems in Estimating a Hurst Exponent--A Case Study of Applications to Climatic Change[J].Scientia Geographica Sinica,2004,24(2):177-182(江田汉,邓莲堂.Hurst指数估计中存在的若干问题--以在气候变化研究中的应用为例[J].地理科学,2004,24(2):177-182) |
| [21] | Tomsett A C,Toumi R.Annual Persistence in Observed and Modelled UK Precipitation[J].Geophysical Research Letters,2001,28(20):3 891-3 894 |
 2015, Vol. 40
2015, Vol. 40



