文章信息
- 刘宁, 张永志, 熊永良
- LIU Ning, ZHANG Yongzhi, XIONG Yongliang
- GPS参考站对流层湿延迟近实时估计的三步滤波算法
- A Three-step Kalman Filter Algorithm for Near Real-time Estimating Tropospheric Wet Delay on GPS Reference Stations
- 武汉大学学报·信息科学版, 2015, 40(7): 918-923
- Geomatics and Information Science of Wuhan University, 2015, 40(7): 918-923
- http://dx.doi.org/10.13203/j.whugis20130600
-
文章历史
- 收稿日期:2013-10-24
2. 西南交通大学地球科学与环境工程学院, 四川 成都, 610031
2. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu 610031, China
对流层湿延迟是由大气中的水汽所引起的,由于水汽分布的不均匀性以及随时间变化的相关性,从而使现有的对流层湿延迟模型改正精度不高,成为影响长距离高精度GPS定位以及进行天气预报、天气变化研究的主要因素。近年来,随着区域CORS系统的建立和运行,且在该系统的数据处理中,存在参考站坐标精确已知及参考站网络冗余观测信息等特点,使得国内外学者对中长基线参考站间整周模糊度与对流层延迟的解算方法展开了相关研究。文献[1]提出了一种建立相对对流层参数吸收对流层双差残差影响的特定几何对流层降相关思想,并结合正则化法来解算长基线,以广州的CORS网数据为例得到了亚cm级的定位结果。Dai对GPS/GLONASS参考站网络中大气延迟误差的空间和时间的相关性进行了研究,并建立了相应的模型进行预测,以提高模糊度实时固定的效率[2];Zinas对利用中心网络参考站处理的方法来提高单历元模糊度解算进行了研究[3];Takasu提出采用扩展卡尔曼滤波的方法进行长基线中模糊度、电离层延迟及对流层参数的准确估计,并以多组基准站的数据对所提方法作了验证[4];沈雪峰基于星型结构对参考站网络RTK中的对流层延迟及模糊度的解算进行了研究[5];杨玲采用自适应滤波算法估计了GNSS基准站间的对流层延迟[6]。虽然这些算法在模糊度解算及对流层延迟估计方面都取得了较好的结果,但未对流层湿延迟的近实时估计作探讨分析,为此,本文在分析上述算法的基础之上,基于组合后的超快星历,提出了适合于GPS参考站对流层湿延迟近实时估计的三步Kalman滤波算法,并以实例验证了本文方法的正确性。
1 三步滤波法近实时估计湿延迟的解算策略 1.1 宽巷模糊度与伪距多路径分离 的Kalman滤波法一般情况下,GPS参考站间的距离可达几十km或上百km,在采用双差模式直接对双频L1、L2相位的模糊度进行分解时,由于无法消除或减弱大气延迟误差,使得原始频率整周模糊度的解算成功率降低,因此,需先对具有较长波长特性的宽巷模糊度进行解算后,再利用宽巷模糊度的固定解来确定原始频率的双差整周模糊度。对于参考站间双差宽巷模糊的计算,可采用双频伪距相位线性组合的方法进行求解,即M-W组合:
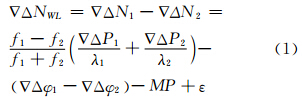
式中,∇ΔNWL、∇ΔN1、∇ΔN2为双差宽巷模糊度、L1及L2频率的双差模糊度,∇ΔP1、∇ΔP2为L1及L2频率的双差伪距观测值,∇Δφ1、∇Δφ2为L1及L2频率的双差载波相位观测值;MP为线性组合后的伪距多路径误差;ε为线性组合后的噪声误差。在利用式(1)的M-W组合求解宽巷模糊度时,需提供L1频率上的精码(P1码),但在实际的测量应用当中,GPS接收机通常无法获取P1码的观测量,若采用C/A码代替P1码,并继续以式(1)进行单历元宽巷模糊度求解时,由于C/A码受伪距多路径的影响较大,且其观测精度不高,从而使宽巷模糊度浮点解的精度往往较差,因此,必须对式(1)中线性组合后的伪距多路径误差与宽巷模糊度进行分离。由于伪距多路径误差不为常量,且与一定的时间间隔存在相关性,同时考虑相位无周跳时整周模糊度存在相等的特性,因此可建立以宽巷模糊度与伪距多路径误差为状态参数的状态方程[7, 8]:
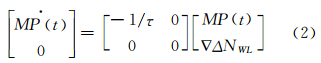
式中,M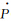 (t)为多路径误差的变化率,τ为相关时间。同时,以式(1)作为离散系统的观测方程,便可建立Kalman方程逐历元计算宽巷模糊度的浮点解及伪距多路径误差的估计值,在获得宽巷模糊度的浮点解及其相应的方差阵后,便可利用LAMBDA方法来快速确定宽巷整周模糊度。由于宽巷模糊度之间的相关性很弱,单个历元即可较好地实现宽巷模糊度的固定,所以,仅对宽巷模糊度的固定解进行OVT(over the time)检验[9],根据OVT检验序列,便可使宽巷模糊度正确的整数解得到确认。
(t)为多路径误差的变化率,τ为相关时间。同时,以式(1)作为离散系统的观测方程,便可建立Kalman方程逐历元计算宽巷模糊度的浮点解及伪距多路径误差的估计值,在获得宽巷模糊度的浮点解及其相应的方差阵后,便可利用LAMBDA方法来快速确定宽巷整周模糊度。由于宽巷模糊度之间的相关性很弱,单个历元即可较好地实现宽巷模糊度的固定,所以,仅对宽巷模糊度的固定解进行OVT(over the time)检验[9],根据OVT检验序列,便可使宽巷模糊度正确的整数解得到确认。
当宽巷模糊度∇ΔNWL得到固定后,为了消除电离层延迟对解算L1模糊度∇ΔN1产生的影响,须建立无电离层延迟组合的双差观测方程[10]:
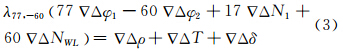
式中,∇Δρ为双差后的卫地距离;∇ΔT为双差后的对流层延迟;λ77,-60为无电离层组合后相位的波长;∇Δδ为无电离层组合后相位的观测噪声。通过分析式(3)可知,宽巷模糊度已被固定,且参考站的坐标精确已知,所以L1模糊度的解算精度主要受双差对流层延迟的影响,需对∇ΔN1与∇Δdtrop进行分离。
由于对流层中的干燥大气比较稳定,且符合理想气体状态方程,因此,本文采用精度可达mm级的UNB 3 m对流层延迟模型及GMF映射函数来直接求解∇ΔT中的干延迟部分。同时,对于中长距离的两参考站,由于两站的卫星高度角(e≥10°)相差较小,因此,与之相对应的湿映射函数是近似相等的。基于此条件,便可对∇ΔT中的湿延迟部分进行近似相等变换以减少待估参数,即利用天顶方向的相对湿延迟RZWD来表达:
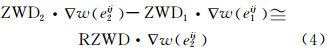
式中,w(e)为湿映射函数;e为卫星高度角;∇为单差算子。 同时,由水汽辐射计实际观测的湿延迟所得到的结果分析表明,天顶湿延迟符合随机游走模型[10],因此,结合式(3)、式(4)便可构建Kalman滤波方程估计以L1双差模糊度(n+1颗卫星)与天顶方向相对湿延迟为未知参数的状态向量 Xn=[∇ΔN11 … ∇ΔN1n RZWD]T,其相应的状态方程为:
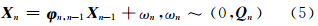
式中,φn,n-1为状态转移矩阵;Qn为状态噪声的方差阵。根据滤波方程逐历元估计出L1双差模糊度的浮点解及相应的方差阵后,同样基于LAMBDA方法来确定参考站间的L1整周模糊度。由于L1双差模糊度对应的波长较短,其模糊度之间的相关性很强,需对每个历元模糊度固定解的质量进行Ratio检验[11]:

式中,N、 、
、 ′分别为L1双差模糊度的浮点解、固定解的最优值及次优值;QNN为L1双差模糊度的方差阵;c为阀值,c=2。显然,Ratio值越大,求解的L1整周模糊度越可靠。同时,在通过Ratio值检验的基础上,附加OVT检验,从而降低误判的可能性,进一步提高L1整周模糊度正确值的可靠性。
′分别为L1双差模糊度的浮点解、固定解的最优值及次优值;QNN为L1双差模糊度的方差阵;c为阀值,c=2。显然,Ratio值越大,求解的L1整周模糊度越可靠。同时,在通过Ratio值检验的基础上,附加OVT检验,从而降低误判的可能性,进一步提高L1整周模糊度正确值的可靠性。
由于双差模糊度本身的整数特性,在未将模糊度正确固定之前,利用消电离层组合模型并通过Kalman滤波估计出的相对对流层湿延迟是不够准确的,因为与其一起分离出的L1模糊度为浮点值,且模糊度浮点值与整数值之间的差异会使相对对流层湿延迟的精度受到影响。因此,本文采用将正确固定的L1双差模糊度进行回代的方法,重新构建Kalman滤波器来估计相对对流层湿延迟参数:

式中,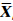 k,k-1为状态参数向量;
k,k-1为状态参数向量;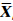 k=RZWD;Hk,k-1为状态转移矩阵,Hk,k-1=1;
k=RZWD;Hk,k-1为状态转移矩阵,Hk,k-1=1;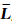 k为观测向量;Bk为系数矩阵,Bk=[∇w(e21)… ∇w(en2)]T;
k为观测向量;Bk为系数矩阵,Bk=[∇w(e21)… ∇w(en2)]T;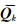 、
、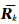 为状态噪声矩阵与观测噪声矩阵,其中,
为状态噪声矩阵与观测噪声矩阵,其中,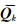 =qΔt。同时,在以式(7)进行求解的过程中,为了获取近实时相对对流层湿延迟,需采用实时的精密卫星星历数据。而IGS提供的超快星历所包含的预报星历(predicted half)可满足实时性的要求,并且该星历每6 h更新一次,对应的发布时间为UTC 03:00、09:00、15:00和21:00。值得注意的是,由于预报星历是通过外推预报得到的,且随着时间跨度的增大,预报星历的精度也随之降低。所以在单天数据解算中,就需选取相应时段的预报星历,并对这些时段的预报星历进行组合以保证卫星星历的实时性及较高的精度[11],再利用式(7)的滤波方程最终解算近实时相对对流层湿延迟。
=qΔt。同时,在以式(7)进行求解的过程中,为了获取近实时相对对流层湿延迟,需采用实时的精密卫星星历数据。而IGS提供的超快星历所包含的预报星历(predicted half)可满足实时性的要求,并且该星历每6 h更新一次,对应的发布时间为UTC 03:00、09:00、15:00和21:00。值得注意的是,由于预报星历是通过外推预报得到的,且随着时间跨度的增大,预报星历的精度也随之降低。所以在单天数据解算中,就需选取相应时段的预报星历,并对这些时段的预报星历进行组合以保证卫星星历的实时性及较高的精度[11],再利用式(7)的滤波方程最终解算近实时相对对流层湿延迟。
采用美国CORS网中P304、P305和P306站 2010-01-03的观测数据作为验证本文方法的实验数据,该数据的采样率为15 s,3个参考站均采用双频GPS接收机观测记录L1、L2载波相位及C/A、P2码,并构成如图 1所示的三角形网络,其中P304、P305和P306站的大地高分别为17.188 3 m、96.049 3 m、82.514 0 m。
|
| 图 1 三个参考站所组成的三角形网络 Fig. 1 Three Reference Stations Composing the Triangle Network |
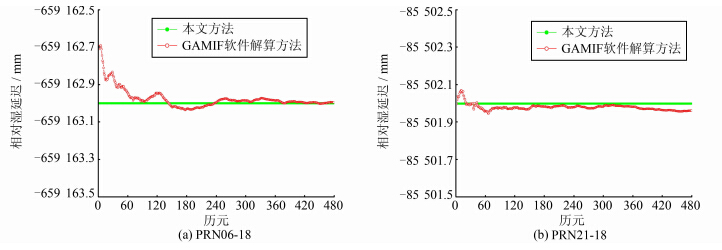
在利用本文方法进行求解的过程中,截止高度角设为10°,选取P305站作为中心参考站并以组合后的超快星历作为单天的星历文件来分别求解P305-P306、P305-P304参考间的近实时相对对流层湿延迟。同时,在中心参考站和星历相同的情况下,采用GAMIT软件中的TRACK模块所解算的相对对流层湿延迟结果作为验证本文方法的参考值。于是可得P305-P306、P305-P304相应的相对湿延迟比较结果如图 2所示。
|
| 图 2 本文方法与GAMIT解算的相对对流层湿延迟比较结果 Fig. 2 Comparison Results of Relative Troposphere Wet Delay Between Proposed Method and GAMIT |
由图 2可以看出,本文方法与GAMIT解算得到的相对对流层湿延迟总体趋势是一致的,且利用本文方法获取的P305-P306站间的相对湿延迟与GAMIT所获取的结果吻合程度较高,优于P305-P304站间的湿延迟结果。同时,计算本文方法与GAMIT两者解算结果的差值来说明本文方法求解相对对流层湿延迟的质量,两站相应的精度信息列于表 1。
| 站名 | 最大误差 | 最小误差 | 平均误差 | 中误差 |
| P305-P306 | 17.0 | -23.1 | -0.9 | 4.7 |
| P305-P304 | 32.5 | -9.2 | 10.4 | 12.4 |
从表 1可知,利用本文提出的方法来求解参考站间相对对流层湿延迟可获得较好的精度,验证了该方法的可行性和正确性。同时也发现,P305-P304站间的解算精度低于P305-P306,其主要原因在于P304站与中心参考站P305高程差异大于P306站,从而影响相对对流层湿延迟的解算,使其精度有所下降。
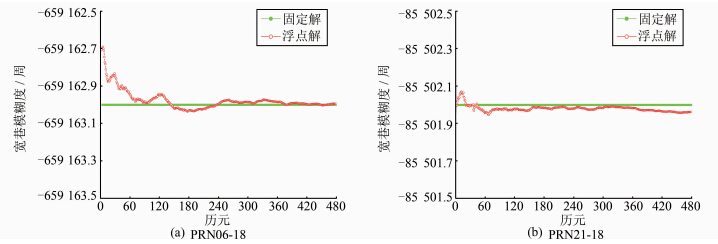
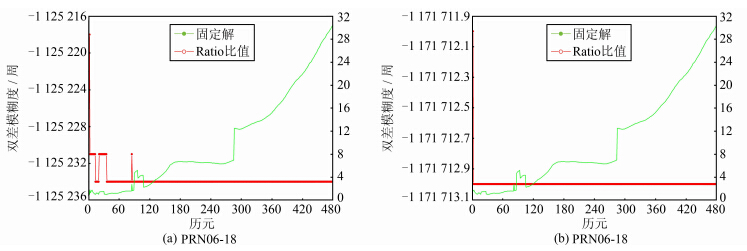
另一方面,为了便于对本文方法固定宽巷模糊度和L1模糊度的情况进行分析,以选取某时段中的两颗卫星PRN06及PRN21为例,与参考卫星PRN18分别构成卫星对PRN06-18、PRN21-18来进行说明,得到两组卫星对双差宽巷模糊度的固定解与浮点解如图 3所示,相应地,两组卫星对的L1双差模糊度的固定过程如图 4所示。
|
| 图 3 两组卫星对宽巷模糊度的固定解与浮点解 Fig. 3 Fixed Solution and Afloat Solution of Wide Integer Ambiguity for Two Sets of Satellite Pair |
|
| 图 4 两组卫星对L1模糊度的固定过程 Fig. 4 Fixed Procedure of L1 Integer Ambiguity for Two Sets of Satellite Pair |
从图 3可以看出,两组卫星对宽巷模糊度的浮点解与整数解的差值远小于±0.5周,单个历元便可固定宽巷模糊度,由此表明,本文所提出的方法在采用Kalman滤波来分离宽巷模糊度与伪距多路径误差时,可获得精度较高的宽巷模糊度浮点解并实现宽巷整周模糊度的快速固定。同时,从图 4可以看出,两卫星对L1模糊度序列在临近历元数为90时,L1双差模糊度都得到固定,对于后续所有历元,Ratio序列值增大,L1双差模糊度的固定解为一条直线序列,表明本文方法解算的L1模糊度固定解是可靠的,且在很大程度上降低了L1模糊度正确解误判的可能性。此外,在由3个参考站所组成的三角形网络中,应该满足3个参考站上相同的卫星对所对应的整周模糊度之和为零的闭合条件[13],因此,将上述两卫星对宽巷整周模糊度及L1整周模糊度的闭合结果列于表 2。
由表 2可知,3个参考站上两卫星对宽巷整周模糊度及L1整周模糊度各自的求和值都为零,满足闭合条件,进一步验证了本文方法在实现宽巷、L1模糊度分解及检验时的正确性。
| 卫星对 | 宽巷整周模糊度 | L1整周模糊度 | 求和 | |
| 宽巷 | L1 | |||
| PRN06-18 | -4 663 560,5 322 723,-659 163 | -4 203 050,5 328 284,-1 125 234 | 0 | 0 |
| PRN21-18 | -3 901 953,3 816 451,85 502 | -2 857 840,4 029 553,-1 171 713 | 0 | 0 |
基于组合后的超快星历,提出了一种参考站对流层湿延迟近实时估计的三步Kalman滤波算法,通过实例分析表明,利用本文提出的方法来求解两组参考站近实时对流层湿延迟可获得较好的精度,验证了该方法的可行性和正确性。同时也发现,对流层湿延迟的解算精度与基线的长度、高程差异的大小有关。此外,该方法在求解宽巷模糊度时,利用Kalman滤波来分离伪距多路径与宽巷模糊度参数,宽巷模糊度浮点解的精度较高,可在单个历元内实现宽巷模糊度的快速固定。并且对于由3个参考站所组成的三角形网络,实例中同一卫星对宽巷模糊度的固定解及L1模糊度的固定解都满足闭合条件。
| [1] | Li B,Feng Y,Shen Y,et al.Geometry-Specified Troposphere Decorrelation for Subcentimeter Real-Time Kinematic Solutions over Long Baselines[J].Journal of Geophysical Research:Solid Earth,2010,115,B11404 |
| [2] | Dai L,Wang J,Rizos C,et al.Predicting Atmospheric Biases for Real-Time Ambiguity Resolution in GPS/GLONASS Reference Station Networks[J].Journal of Geodesy,2003,76(11/12):617-628 |
| [3] | Zinas N,Parkins A,Ziebart M.Improved Network-Based Single-Epoch Ambiguity Resolution Using Centralized GNSS Network Processing[J].GPS Solutions,2013,17(1):17-27 |
| [4] | Takasu T,Yasuda A.Kalman-Filter-Based Integer Ambiguity Resolution Strategy for Long-Baseline RTK with Ionosphere and Troposphere Estimation[C].Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation,Portland,Oregon,2010 |
| [5] | Shen Xuefeng,Gao Chengfa,Pan Shuguo.Algorithm for Network RTK (VRS) Based on Star Structure[J].Acta Geodaetica et Cartographica Sinica,2012,41(1):33-40(沈雪峰,高成发,潘树国.基于星型结构的虚拟参考站网络实时动态测量关键算法研究[J].测绘学报,2012,41(1):33-40) |
| [6] | Yang Ling,Shen Yunzhong,Li Bofeng.Adaptive Filter for Computing Tropospheric Delay on GNSS Reference Stations[C].CPGPS 2010 Navigation and Location Services:Emerging Industry and International Exchanges,Shanghai,2010 |
| [7] | Yang Y,Hatch R R,Sharpe R T.GPS Multipath Mitigation in Measurement Domain and Its Applications for High Accuracy Navigation[C].Proceedings of the ION GNSS Long Beach,California,2004 |
| [8] | Fan Jianjun,Yong Shaowei,Wang Feixue.Study on Multipath Mitigationand Dual-Frequency Fast Ambiguity Estimation Basedon Kalman Filter[J].Journal of Electronics&Information Technology,2008,30(5):1 075-1 079(范建军,雍少为,王飞雪.基于卡尔曼滤波的多径误差消除及双频模糊度快速估计方研究[J].电子与信息学报,2008,30(5):1 075-1 079) |
| [9] | Meng Lingpo,Wu Jie.Research on Ambiguity Dynamic Resolution Using Dual Frequency Single-Epoch Data[J].Journal of National University of Defense Technology. 2010,32(1):34-39(孟领坡,吴杰.双频去相关单历元动态解算整周模糊度研究[J].国防科技大学学报,2010,32(1):34-39) |
| [10] | Li Zhenghang,Zhang Xiaohong.New Techniques and Precise Data Processing Methods of Satellite Navigation and Positioning[M].Wuhan:Wuhan University Press,2009(李征航,张小红.卫星导航定位新技术及高精度数据处理方法[M].武汉:武汉大学出版社,2009) |
| [11] | Xu Shaoguang,Xiong Yongliang,Liu Ning.et al.Real-time PWV Obtained by Ground GPS[J].Geomatics and Information Science of Wuhan University,2011,36(4):407-411(徐韶光,熊永良,刘宁,等.利用地基GPS获取实时可降水量[J].武汉大学学报·信息科学版),2011,36(4):407-411) |
| [12] | Deng Jian,Wang Qing,Pan Shuguo.Fast Integer Ambiguity Resolution Methodfor low Elevation Satellites in Network RTK Reference Stations[J].Chinese Journal of Scientific Instrument,2010,31(6):1 201-1 206(邓健,王庆,潘树国.网络RTK参考站间低仰角卫星模糊度快速解算方法[J].仪器仪表学报,2010,31(6):1 201-1 206) |
| [13] | Ke Fuyang,Wang Qing,Pan Shuguo.Research on long Baseline Ambiguity Resolution of Network RTK[J].Journal of Geodesy and Geodynamics,2012,32(5):72-77(柯福阳,王庆,潘树国.网络RTK长基线模糊度解算方法研究[J].大地测量与地球动力学,2012,32(5):72-77) |
 2015, Vol. 40
2015, Vol. 40



