文章信息
- 姚朝龙, 罗志才, 刘立龙, 周波阳
- YAO Chaolong, LUO Zhicai, LIU Lilong, ZHOU Boyang
- 顾及地形起伏的中国低纬度地区湿延迟与可降水量转换关系研究
- On the Relation Between the Wet Delay and the Water Precipitable Vapor in Consideration of Topographic Relief in the Low-latitude Region of China
- 武汉大学学报·信息科学版, 2015, 40(7): 907-912
- Geomatics and Information Science of Wuhan University, 2015, 40(7): 907-912
- http://dx.doi.org/10.13203/j.whugis20130409
-
文章历史
- 收稿日期:2013-08-13
2. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉, 430079;
3. 武汉大学地球空间信息技术协调创新中心, 湖北 武汉, 430079;
4. 桂林理工大学测绘地理信息学院, 广西 桂林, 541004;
5. 广西空间信息与测绘重点实验室, 广西 桂林, 541004;
6. 广东工业大学测绘工程系, 广东 广州, 510006
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China;
3. Collaboracive Innovation Center for Geospatial Technology, Wuhan University, Wuhan 430079, China;
4. College of Geodesy and Geomatics, Guilin University of Technology, Guilin 541004, China;
5. Guangxi Key Laboratory of Spatial Information and Geomatics, Guilin 541004, China;
6. Department of Surveying and Mapping, Guangdong University of Technology, Guangzhou 510006, China
在地基GPS反演大气可降水量(precipitable water vapor,PWV)过程中,首先从天顶对流层延迟(zenith troposphere delay,ZTD)中减去天顶干延迟 (zenith hydrostatic delay,ZHD),得到与大气水汽相关的天顶湿延迟(zenith wet delay,ZWD),ZWD再乘以转换系数K,从而获得天顶方向上的PWV。因此,ZWD与PWV的转换系数K是地基GPS气象学研究的关键参数。
在实际应用中,为了获得GPS PWV,一般可以取K为常数0.15[1]或通过Bevis模型[2]或建立局地加权平均温度模型[3]计算得到。在建立Tm模型方面,Bevis等[4]通过线性回归获得了可广泛用于中纬度地区的基于地面温度的Tm模型。姚宜斌等[5]提出了一种可以利用测站三维坐标和年积日直接进行计算的加权平均温度的新模型GWMT。李建国等[6]建立了适用于中国东部的Tm线性回归模型;于胜杰等[7]给出了与测站高度相关的误差改正后的Bevis模型;王晓英等[8, 9, 10]分析了Tm与地面温度、气压和水汽压的关系,建立了适合中国大陆地区的Tm-Ts经验公式,并在缺少历史探空数据的地区利用ECMWF再分析产品建立了局地Tm-Ts经验公式;文献[11]建立了与温度、气压和湿度相关的Tm模型,该模型适用于青藏高原地区。此外,为了避免气压、温度等气象数据的误差影响,于胜杰等[12]还研究了利用拟合得到的PWV与ZTD间的线性关系获得PWV的方法。
以上计算K值的方法大多是通过Tm模型求得,Emardson等[13]提出了直接利用测站纬度和年积日计算转换系数K的模型。之后,Emardson 等[14]根据不同的气候类型将欧洲划分为4个区域,并利用该方法建立了相应的区域K值模型。曲建光[15]选取了北京、武汉和拉萨3个站对比分析了通过Tm或利用测站纬度和年积日计算转换系数K的两种方法。
根据文献[5, 7]的研究结果,对于大范围区域,测站海拔也是影响K值的因素之一。因此,本文借鉴文献[13]提出的K值模型,利用中国低纬度地区(20.03°N~28.2°N)20个探空站2008~2011年的探空数据,在分析K值随纬度和海拔变化特征的基础上,建立与站点纬度、年积日和海拔相关的单站和区域转换系数K值模型,并与传统的通过Tm求解转系数K值的方法进行比较,分析区域模型在该地区的适用性。
1 转换系数K的计算方法GPS PWV可由式(1)计算:
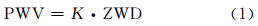
其中,

式中,Rv为水汽特定的气体常数;ρ为水的密度;k′2=22.1 K/hPa;k3=3.739·105 K2/hPa;Tm为加权平均温度。
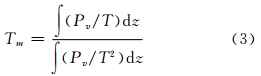
实际计算中,探空数据提供了从地面到不同高度层的温度Ti和水汽压Pw,i,因此,将式(3)离散化后可得:

式中,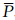 w,i和
w,i和 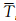 i分别为从高度为hi到高度为hi+1的平均水汽压和平均温度,
i分别为从高度为hi到高度为hi+1的平均水汽压和平均温度,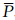 w,i=
w,i= (Pw,i+1+Pw,i);
(Pw,i+1+Pw,i);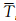 i=
i= (Ti+1+Ti)。 通过式(4)可以精确计算出加权平均温度。然而,在实际应用中不可能在每个GPS站同时获得探空观测数据。根据Bevis的研究[4],Tm可以通过地面温度(T)计算得到:
(Ti+1+Ti)。 通过式(4)可以精确计算出加权平均温度。然而,在实际应用中不可能在每个GPS站同时获得探空观测数据。根据Bevis的研究[4],Tm可以通过地面温度(T)计算得到:
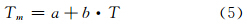
式中,系数a、b可利用最小二乘法计算得到。 Bevis通过线性回归获得了适用于中纬度地区的基于地面温度的 Tm模型:
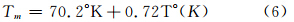
Emardson等提出了利用测站纬度和年积日计算转换系数K的模型[13]:
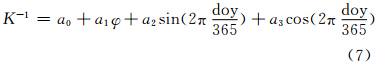
式中,φ为测站纬度;doy为年积日;a0、a1、a2、a3可通过最小二乘方法求得。
2 转换系数K的空间分布特征利用中国低纬度地区20个探空站2008~2011年的探空数据通过式(4)获得精确的转换系数K,分析K值在该地区随纬度和海拔的空间变化特征。
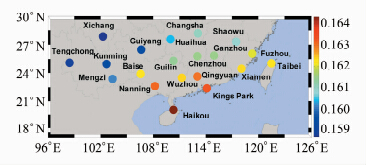
图 1给出了20个探空站2008~2011年平均K值的变化情况。从图中可以看出,总体上低纬度地区的K值高于高纬度地区,纬度最低的Haikou站(20.03°N)平均K值达到了0.164 4,纬度最高的Changsha站(28.2°N)平均K值为0.161 1;低海拔地区的K值高于高海拔地区,海拔最低的Taibei站(9.0 m)平均K值为0.162 3,海拔最高的Kunming站(海拔1 892 m)平均K值为0.159 5;纬度和海拔接近的情况下,沿海地区的K值大于内陆地区,例如沿海地区的Fuzhou站(26.08°N,海拔85 m)平均K值为0.162 0,而内陆地区的Ganzhou站(26.48°N,海拔125 m)的平均K值为0.161 5。由此可以看出,转换系数K受地理位置、地形起伏以及气候类型的综合影响。
|
| 图 1 各探空站2008~2011年平均K值 Fig. 1 Mean Value of K from 2008 to 2011 at Each Site |
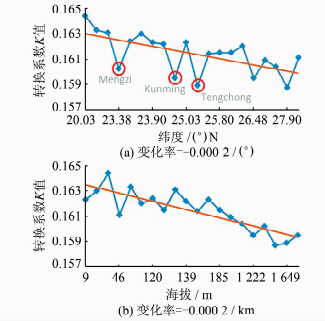
图 2更好地反映出平均K值随纬度和海拔的变化趋势,从图 2(a)可以看出,随着纬度的增加平均K值呈现出逐渐减小的整体趋势,变化率为-0.000 2/(°)。其中Mengzi、Kunming和Tengchong等3个站的K值突然减小,是因为这3个站的海拔出现了突然的增大,相对于纬度的变化,此时海拔变化的影响更大,而如果单独考虑这3个高海拔探空站,其平均K值的变化趋势仍然是随着纬度的增大而减小。图 2(b)中,平均K值随着海拔的增大而逐渐减小,并且这种趋势比图 2(a)的趋势更为明显,变化率为-0.002/km。
|
| 图 2 各探空站平均K值随纬度和海拔的变化趋势 Fig. 2 Mean K Value Varies with Latitude and Height at Each Site |
通过以上分析可知,转换系数K不仅受测站地理位置(纬度)的影响,而且还与地形起伏(海拔)有关。因此,本文在式(7)的基础上,加入了测站海拔的影响,其公式如下:
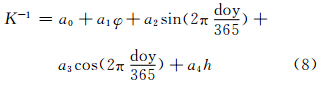
式中,h为测站海拔,单位为m;a4为其相应的系数,其余变量与式(7)相同。
3 区域K值模型及其精度分析通过15个探空站2008~2011年的探空数据利用式(7)分别建立各探空站的单站K值模型(称为“单站模型”)以及利用所有探空站数据建立相应的区域K值模型(称为“区域模型1”),同时利用式(8)建立了考虑地形起伏的区域K值模型(称为“区域模型2”)。此外,采用式(5)、式(6)计算了各站的K值,分别称为线性回归模型和Bevis模型,与区域模型1和区域模型2作对比分析。最后利用其余5个探空站2008~2012年的数据检验两种区域模型的外符合精度。
从表 1给出的区域模型1和区域模型2相应的参数可以看出,虽然系数a4的值很小,对于海拔低于500 m的测站,其对K值的影响仅为0.000 1,但在考虑测站海拔的影响后,系数a0和a1发生了较大的变化,而系数a2和a3几乎保持不变,说明测站海拔和测站纬度均是影响K值的因素,而且两者具有相关性。
| 模型 | a0 | a1 | a2 | a3 | a4 |
| 区域模型1 | 0.173 70 | -0.000 50 | -0.001 12 | -0.002 63 | - |
| 区域模型2 | 0.172 23 | -0.000 40 | -0.001 12 | -0.002 62 | -0.000 002 |
图 3为不同模型计算各站的K值相对于式(4)计算的K值(真值)的均方根误差(RMS)。从图中可以看出,通过线性回归模型计算的K值的精度最高,RMS小于0.001 7。由于Bevis模型是利用美国部分探空站通过线性回归得到的,该模型在中国低纬度地区的精度略低于局地线性回归模型,而且其精度随着纬度的减小而降低,从Huaihua站(27.56°N)RMS为0.0018到Haikou站(20.03°N)RMS达到了0.002 6。单站模型的精度与Bevis模型计算的K值精度相当,在纬度较低的地区单站模型具有较高的精度,而较高纬度的几个站点的精度略低,精度最低的Xichang站其RMS为0.002 5。由于区域模型的建立受到站点分布、地形起伏以及气候类型等多种因素的综合影响,因此,其精度相比于其他单站计算的K值的精度略低。而由于区域模型1未考虑地形起伏的影响,其精度略低于区域模型2的精度。区域模型1和区域模型2精度最低的站点均是Changsha站,RMS分别为0.003 1和0.002 8,这可能与该站探空数据的质量稍差有关。在不考虑ZWD误差的情况下,由式(1)可以得到转换系数K的误差与PWV误差的相关关系为: δPWV=ZWD·δK。由此,在中国低纬度最潮湿的沿海地区,ZWD一般在500 mm以内,此时线性回归模型、Bevis模型、单站模型、区域模型1和区域模型2误差引起的PWV最大估算误差分别为0.85 mm、1.30 mm、1.25 mm、1.55 mm和1.40 mm。

|
| 图 3 不同模型计算K值精度情况 Fig. 3 Precision of K Using Different Models |
通过以上分析可知,线性回归模型和Bevis模型计算K值精度较高,但需要已知地面温度,因此,无法用于缺少气象观测的区域。而单站模型无法应用到离测站较远的地区。两种区域模型适用于整个区域并且不需要任何气象数据。此外,当考虑地形起伏的影响时,区域模型2的精度得到了一定的改善。
为了分析区域模型的外符合精度,在沿海地区(Xiamen站)、内陆低海拔地区(Chenzhou站、 Baise站、Qingyuan站)和高海拔地区(Guiyang 站)共选取5个站用于检验两种区域模型的外符合精度。
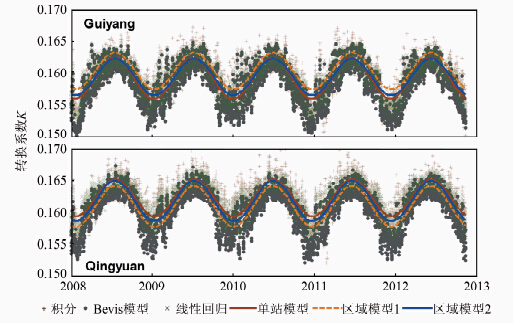
表 2可以看出,区域模型2在5个站的外符合精度均高于区域模型1的精度,特别是在Guiyang和Qingyuan两个站精度均有了较为明显的提高,RMS分别从0.002 3和0.002 1降到0.001 8,其余3个站的精度略有提高。整体上,两种区域模型的外符合精度与其内符合精度相当。图 4给出了不同方法得到的Guiyang站和Qingyuan站转换系数K值,从图中可以看出,Bevis模型、线性回归模型、单站模型和两种区域模型计算的K值与积分值均具有很好的一致性。区域模型1计算的K值与单站模型的K值存在较大偏差,在考虑地形起伏影响后,区域模型2获得的K值与单站模型的K值较为接近。总体上,区域模型2计算的K值处于单站模型和区域模型1计算的K值之间。此外,Bevis模型计算的K值随着纬度的降低(从Guiyang站26.48°N到Qingyuan站23.66°N)与积分值的偏差越来越大。
| 站点 | 区域模型1 | 区域模型2 | ||
| MAE | RMS | MAE | RMS | |
| Guiyang | 0.001 9 | 0.002 3 | 0.001 5 | 0.001 8 |
| Chenzhou | 0.001 9 | 0.002 3 | 0.001 8 | 0.002 3 |
| Xiamen | 0.001 5 | 0.001 9 | 0.001 4 | 0.001 8 |
| Baise | 0.001 7 | 0.002 2 | 0.001 7 | 0.002 1 |
| Qingyuan | 0.001 7 | 0.002 1 | 0.001 5 | 0.001 8 |
|
| 图 4 不同方法计算Guiyang站和Qingyuan站K值 Fig. 4 K Values Calculated by Different Methods at Guiyang Site and Qingyuan Site |
通过Tm计算转换系数K值,通常需要已知测站的气象参数,且单站模型的应用范围有限。本文利用中国低纬度地区探空站数据分析了该地区湿延迟与可降水量间的转换关系,发现转换系数K值分别随着纬度和海拔的增大而减小。在考虑地形起伏(测站海拔)影响的条件下,建立了适用于该地区的区域转换系数K值模型。该模型在区域内任何站点不需要已知测站气象参数,仅通过站点纬度、年积日和海拔即可获得高精度的转换系数K,其精度与单站模型或者通过Tm计算得到的K值精度相当,可用于该地区无气象数据条件下GPS反演PWV。
| [1] | Wang Yong,Liu Yanping,Liu Lintao,et al.Retrieval of the Change of Precipitable Water Vapor by GPS Technique[J].Geo-spatial Information Science,2007,10(4):265-268 |
| [2] | Cao Yunchang,Fang Zongyi,Xia Qing.Relationship Between GPS Precipitable Water Vapor and Precipitation[J]. Journal of Applied Meteorological Science,2005,16(1):54-59(曹云昌,方宗义,夏青.GPS遥感的大气可降水量与局地降水关系的初步分析[J].应用气象学报,2005,16(1):54-59) |
| [3] | Chen Yongqi,Liu Yanxiong,Wang Xiaoya,et al.GPS Real-Time Estimation of Precipitable Water Vapor:Hong Kong Experiences[J].Acta Geodaetica et Cartographica Sinica, 2007,36(1):9-12(陈永奇,刘焱雄,王晓亚,等.香港实时GPS水汽监测系统的若干关键技术[J].测绘学报,2007,36(1):9-12) |
| [4] | Bevis M,Businger S,Herring T A,et al.GPS Meteorology:Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J].J Geophys Res,1992,97(D14):15 787-15 801 |
| [5] | Yao Y B,Zhu S,Yue S Q.A Globally Applicable,Season-Specific Model for Estimating the Weighted Mean Temperature of the Atmosphere[J].J Geod,2012,86:1 125-1 135 |
| [6] | Li Jianguo,Mao Jietai,Li Chengcai.The Approach to Remote Sensing of Water Vapor Based on GPS and Linear Regression Tm in Eastern Region of China[J].Acta Meteorologica Sinica,1999,57(3):283-292(李建国,毛节泰,李成才.使用全球定位系统遥感水汽分布原理和中国东部地区加权"平均温度"的回归分析[J].气象学报,1999,57(3):283-292) |
| [7] | Yu Shengjie,Liu Lintao.Validation and Analysis of the Water-Vapor-Weighted Mean Temperature from Tm-Ts Relationship[J].Geomatics and Information Science of Wuhan University, 2009,34(6):741-744(于胜杰,柳林涛.水汽加权平均温度回归公式的验证与分析[J].武汉大学学报·信息科学版,2009,34(6):741-744) |
| [8] | Wang Xiaoying,Song Lianchun,Dai Ziqiang.Feature Analysis of Weighted Mean Temperature Tm in Hong Kong[J].Journal of Nanjing University of Information Science and Technology:Natural Science Edition,2011,3(1):47-52(王晓英,宋连春,戴仔强.香港地区加权平均温度特征分析[J].南京信息工程大学学报·自然科学版,2011,3(1):47-52) |
| [9] | Wang Xiaoying,Dai Ziqiang,Cao Yunchang,et al.Weighted Mean Temperature Tm Statistical Analysis in Ground-Based GPS in China[J].Geomatics and Information Science of Wuhan University,2011,36(4):412-416(王晓英,戴仔强,曹云昌,等.中国地区地基GPS加权平均温度Tm统计分析[J].武汉大学学报·信息科学版,2011,36(4):412-416) |
| [10] | Wang Xiaoying,Song Lianchun,Cao Yunchang.Analysis of Weighted Mean Temperature of China Based on Sounding and ECMWF Reanalysis Data[J].Acta Meteor Sinica, 2012,26(5):642-652 |
| [11] | Qin J,Yang K,Koike T,et al.Evaluation of AIRS Precipitable Water Vapor Against Ground-Based GPS Measurements over the Tibetan Plateau and Its Surroundings[J]. Journal of the Meteorological Society of Japan, 2012,90:87-98 |
| [12] | Yu Shengjie,Liu Lintao.Study on Preciptable Water Vapor Without Meteorological Data[J].Journal of Geodesy and Geodynamics,2008,28(5):34-38(于胜杰,柳林涛.无地面温压数据的可降水量研究[J].大地测量与地球动力学,2008,28(5):34-38) |
| [13] | Emardson T R,Elgered G,Johansson J M.Three Months of Continuous Monitoring of Atmospheric Water Vapor with a Network of Global Positioning System Receivers[J].J Geophys Res, 1998,103:1 807-1 820 |
| [14] | Emardson T R,Derks H J P.On the Relation Between the Wet Delay and the Integrated Precipitable Water Vapor in the European Atmosphere[J].Meteorol Appl,2000(7):61-68 |
| [15] | Qu Jianguang.Calculation and Analysis of Transformation Coefficient K Value of Calculating Integrated Water Vapor[J].Journal of Heilongjiang Institute of Technology,2002,16(3):35-37(曲建光.推算大气综合水汽转换系数K值的计算与分析[J].黑龙江工程学院学报,2002,16(3):35-37) |
 2015, Vol. 40
2015, Vol. 40



