文章信息
- 马洋, 欧吉坤, 袁运斌, 霍星亮, 丁文武
- MA Yang, OU Jikun, YUAN Yunbin, HUO Xingliang, DING Wenwu
- 导航卫星天线相位中心变化估计及对LEO精密定轨影响
- Estimation of GPS Antenna Phase Center Variation and Its Effect on Precise Orbit Determination of LEOs
- 武汉大学学报·信息科学版, 2015, 40(7): 894-900
- Geomatics and Information Science of Wuhan University, 2015, 40(7): 894-900
- http://dx.doi.org/10.13203/j.whugis20130626
-
文章历史
- 收稿日期:2013-10-30
2. 中国科学院大学, 北京, 100049
2. University of the Chinese Academy of Sciences, Beijing 100049, China
GNSS观测值测量的是导航卫星发射天线相位中心到接收机天线相位中心之间的距离。而实际数据处理中,描述导航卫星精密位置的参考点是卫星的质心。只有精确确定导航卫星天线相位中心到卫星质心之间的导航卫星天线相位中心改正信息,才能满足高精度定位和LEO精密定轨等领域的需求。
从2006年12月开始,绝对相位中心改正已取代相对相位中心改正[1, 2]。对于导航卫星端,由于卫星天线受各种复杂太空环境的影响,其特性会发生较大变化,在发射前测定的天线PCV结果无法满足高精度定轨定位的需求,于是德国地球科学研究中心 (Geoforschungszentrum,GFZ)和德国慕尼黑工业大学(Technische Universitt München,TUM)等IGS机构的很多专家基于地面数据对导航卫星PCV的在轨测定展开了研究[1, 2, 3],但是天底角只局限在0~14°的范围。这对分析较高轨道的LEO的星载GPS数据是不够的,比如JASON-2卫星数据对应的最大天底角达到17°,要进一步提升LEO精密定轨的精度,就需要对其做更细致的考虑。
轨道高度约300~1 300 km的高精度LEO平台为导航卫星天底角15°~17°部分的PCV标定提供了重要的数据来源。伯尔尼大学天文研究所(Astronomical Institute of the University of Bern,AIUB)和欧空局航天操作中心(European Space Operations Centre,ESOC)均利用LEO卫星的星载数据,采用直接法同时估计LEO和GPS卫星的PCV[4, 5]。IGS参考了这两个机构解算的结果,在igs08_1745.atx[6]中更新了GPS导航卫星的天底角15°~17°部分的PCV。
Haine等于2004年基于LEO数据的残差初步建立了导航卫星随天底角和方位角的天线变化图[7],本文借鉴了这个思路,采用JASON-2数据,建立了天底角0~17°的导航卫星发射天线的相位中心变化模型。
关于GLONASS卫星发射天线的PCV建模,AIUB和ESOC的专家基于地面观测数据展开了相关研究[8, 9]。随着我国北斗卫星系统的不断建设,2012年年底已经实现了亚太地区的覆盖,在不久的将来,将会有更多的低轨卫星搭载星载GNSS接收机实现精密定轨,所以需要开展此方面的研究,为北斗导航卫星天线相位中心变化在轨标定提供参考。
另外,国内很多学者探讨了GPS导航卫星天线相位中心模型对定位方面的影响[10, 11],但鲜有学者展开其对LEO精密定轨的影响研究。
鉴于此,本文以GPS系统为例,首先基于JASON-2卫星星载GPS精密定轨消电离层组合残差数据,探讨和建立了GPS导航卫星发射天线相位中心变化模型,然后通过与IGS的PCV比较和JASON-2精密定轨进行了验证,最后探讨了GPS的PCV对JASON-2精密定轨的影响。
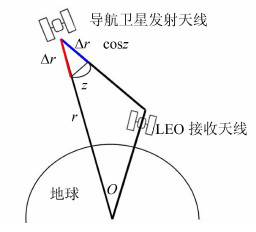
1 数学模型本文基于LEO平台的星载GPS数据标定导航卫星的PCV,图1为解算原理关系示意图[12]。
|
| 图 1 LEO标定导航卫星天线相位中心原理示意图 Fig. 1 Relationship Between Satellite and LEO Receiver Antenna Phase Center |
图1中,r为导航卫星到地心的距离;z为导航卫星天底角;Δr为导航卫星天线相位中心偏差。
对于某LEO卫星观测到的一颗导航卫星(为便于说明,本文理论推导及后面的估计策略均以一颗导航卫星为例),其观测值因为卫星发射天线相位中心偏差Δr及变化PCV引起的距离改正可表示为:
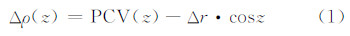
如果其他误差修正较为合理,倘若在精密定轨时不引入导航卫星天线相位中心变化值 PCV,其会在残差数据中体现出来。
考虑到LEO精密定轨中引入的IGS提供的天线相位中心偏差和精密卫星钟差等产品可能存在较小的误差,这些也会表现在定轨的残差中。LEO精密定轨的残差中包含以下几个部分:

式中,Re s(z)为精密定轨之后导航卫星对应的天底角为z时的残差;PCV(z)为相应导航卫星天线相位中心变化;δr为IGS公布的GPS导航卫星天线相位中心偏差残余误差;ΔρT为CODE公布的导航卫星的精密产品的综合误差等项;ε为残余的观测噪声。
式(2)改写成:
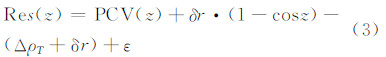
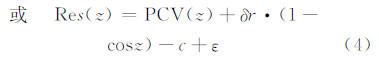
式中,c=(ΔρT+δr)。
由上式可以看出,δr·(1-cosz)为由于存在天线相位中心偏差误差项导致的一个与天底角有关的趋势项,而c是由于天线相位中心偏差误差、卫星钟差误差和模糊度参数等之间有着很强的相关性,难以完全分离而形成的一个组合常数项[12]。也就是说由于定轨解算中引入的产品中存在的多项误差,导致精密定轨的残差中不仅包含平滑的PCV,还存在一个常数项ci和一个与天底角有关的趋势项δr·(1-cosz)。
另一方面,我们考虑将导航卫星天线相位中心变化天底角拓展到17°。由图1可知,低轨卫星的观测值对应的导航卫星最大天底角比在地面上的要大[5, 12],这就为我们提供了可用的数据。以JASON-2为例,其卫星高度约为1 336 km,可观测的最大天底角达到约17°。
为了更好的了解LEO观测数据在导航卫星各天底角处的分布,特对JASON-2卫星共39 d(2012年1~13日,121日~133日,241~253日)的观测数据分布情况进行了统计,详见图2。

|
| 图 2 观测值随天底角分布图 Fig. 2 Distribution of Observations with Respect to the Satellite Nadir Angle |
由图2和表1可以看出,JASON-2大部分观测值分布在导航卫星高天底角部分,其中有约44%的数据分布在天底角大于14°的部分,因此需要将天线相位中心变化天底角拓展至17°。
| 天底角分布 | 观测值数量 | 百分比/% |
| 大于14° | 386 222 | 43.8 |
| 小于14° | 495 405 | 56.2 |
本文思路是利用LEO精密定轨中消电离层观测值的残差,建立与天底角有关的导航卫星天线相位中心变化模型。其具体过程如下。
1) 首先引入CODE精密轨道和钟差产品,固定IGS08.atx中GPS导航卫星发射天线天线相位中心偏差PCO和IGG(Institute of Geodesy and Geophysics)使用的LEO的PCO,另外还引入基于LEO精密定轨残差建模得到的LEO的PCV格网模型,这一部分本文不做讨论,可参考文献[7, 13],然后采用消电离层组合观测数据进行非差简化动力学精密定轨,最后从定轨残差中提取包含常数项和趋势项的PCVraw。
由于包含趋势项和常数项的导航卫星天线相位中心变化具有连续性,为了拟合更光滑,这里用一个以天底角为变量的一元四次函数来描述PCVraw:
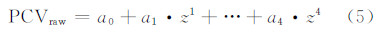
式中,a0,…,a4为一元四次多项式系数;z为天底角。
将LEO精密定轨后得到的某一导航卫星的所有观测残差Res作为观测数据,利用最小二乘残差平方和最小准则
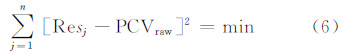
平差解算,即可得到系数的估值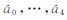 。然后利用式(7)插值得到 1°分辨率的PCVraw:
。然后利用式(7)插值得到 1°分辨率的PCVraw:
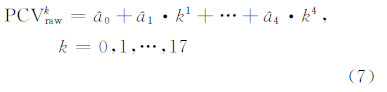
2) 从PCVraw中分离出常数项和趋势项,得到平滑的PCVnew。参考式(4),PCVraw可表达成:

考虑到目前IGS中的PCO和PCV的0~14°部分(基准为0~14°平滑,参见文献[2, 3])是基于地面数据解算得到,并且精密轨道和精密钟差也都是采用地面数据解算得到,天底角也都位于0~14°,为了很好地分离出残余的导航卫星PCO和钟差影响,本文也选取PCVs中0~14°部分平滑[12, 14],来分离得到常数项c和趋势项δr,进而得到天底角0~17°部分的PCVs。
此时,利用PCVrawk( k=0,1,…,14)作为观测数据,利用准则(9),进行最小二乘平差解算,即可得到δr和c的估值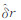 和
和 。
。

将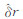 和
和 的估值代回式(8),可得到0 ~17°的PCVnew,即
的估值代回式(8),可得到0 ~17°的PCVnew,即
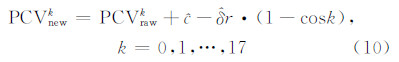
3) 迭代。由于本文的解算是基于精密定轨的残差进行分析处理,部分PCV在精密定轨中可能被其他参数所吸收,所以上述估计过程需要迭代。在迭代时引入新的导航卫星PCVnew(同类型卫星的PCV取平均),整个迭代过程停止迭代的标准是几类GPS卫星0~14°部分的PCV改正量标准差小于1 mm,本文的结果迭代两次。 其具体处理流程如图3所示。

|
| 图 3 导航卫星PCV解算流程图 Fig. 3 Flowchart of Resolutions of GPS PCV |
首先对JASON-2卫星简化动力学精密定轨中的三段共39 d(2012年1~13日,121~133日,241~253日)的残差数据进行了统计,每一段都包含一个JASON-2轨道重复周期。这段时间中,GPS导航卫星共有5类:IIF、IIR-B、IIA、IIR-M、IIR-A,其中,PRN24无数据,PRN27天线类型有更换,所以未做统计。图4是不同卫星的统计结果,由于同类卫星残差图很相似,这里每一类只给出一颗卫星的结果。

|
| 图 4 5类GPS卫星残差分布图 Fig. 4 Distribution of Residuals from Five Kinds of Satellites |
由图4可以看出,残差图中各类卫星的残差分布有明显的连续性和系统性,这就意味着可以利用数学模型去拟合这些残差;另外,还可以看出IIR-B和IIR-M系列天线的残差图十分相似,在后面的PCV解算中也发现这两类卫星的PCV差异很小,所以在最终PCV中将两类卫星合为一类。
由图5可以看出,进行第3次解算后,得到0~14°部分的PCV改正值标准差已低于1 mm(图5(b)),由此得到最终的PCV。
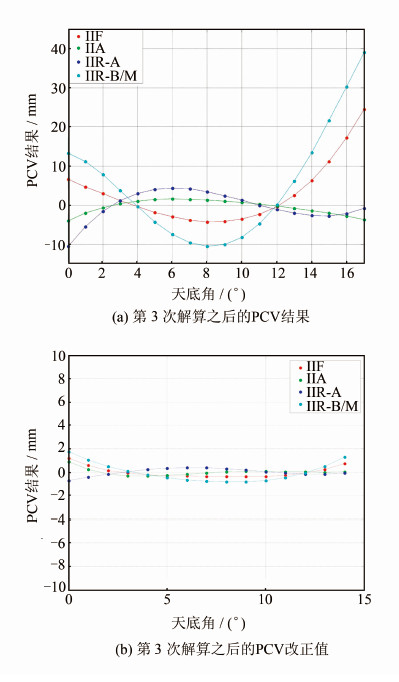
|
| 图 5 迭代解算过程中PCV演变图 Fig. 5 PCVs During the Iteration |
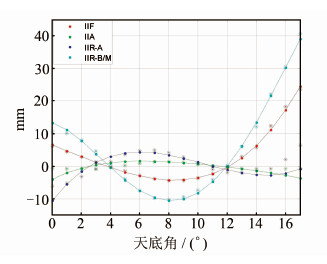
图6和表2显示的是本文估计所得天线相位中心变化值与IGS08.atx的比较,可以看出,在天底角0~17°范围内,只有天底角0°和17°部分由于处于模型边缘且0°附近数据较少,所以存在略大一点的偏差(IIR-A略差),其余部分与IGS结果基本吻合,差异在1~2 mm。
|
| 图 6最终PCV与IGS08的比较及差异图 (图中*为IGS值;·为本文结果) Fig. 6Comparison and Differences Between the Final IGG PCVs and PCVs from IGS08 |
| /mm | ||||
| 统计值区域及类型 | IIF卫星 | IIA卫星 | IIR-A卫星 | IIR-M卫星 |
| 均值(0~17°) | 0.0 | 0.6 | 1.2 | 0.3 |
| 标准差(0~17°) | 0.6 | 1.6 | 3.1 | 1.2 |
| 均值(1~14°) | 0.1 | 0.2 | 0.3 | 0.2 |
| 标准差(1~14°) | 0.4 | 0.6 | 1.1 | 0.7 |
为了进一步验证本文方法所得结果的有效性和分析导航卫星发射天线相位中心变化对LEO精密定轨的影响,选取了2012-01-16~2012-01-25共一个轨道重复周期的数据。设计了以下几种方案(各方案中除导航卫星PCV不同之外,其他定轨模型和策略完全一样),具体说明见表3。
| 方案 | 说明 |
| 方案1 | 0~17°全部为0 |
| 方案2 | 0~14°采用IGS结果, 15~17°采用14°值常数延伸 |
| 方案3 | 0~17°全部采用本文结果 |
| 方案4 | 0~14°IGS结果 ,15~17°本文结果 |
| 方案5 | 0~17°全部采用IGS最新结果 |
为了分析因PCV的不同导致的绝对定轨误 差,将五种方案的定轨结果与JPL精密轨道进行比较,结果见表4。
| (2012-01-16~2012-01-25)/cm | ||||
| 方案 | 径向 | 切向 | 法向 | 3D-RMS |
| 方案1 | 2.36 | 2.62 | 1.54 | 3.84 |
| 方案2 | 1.28 | 2.45 | 1.39 | 3.10 |
| 方案3 | 0.81 | 2.52 | 1.36 | 2.98 |
| 方案4 | 0.81 | 2.53 | 1.36 | 2.98 |
| 方案5 | 0.80 | 2.52 | 1.33 | 2.96 |
由表4可以看出,方案1的结果表明,导航卫星PCV对JASON-2定轨结果影响有mm~cm级,如果不进行改正,会带来约2cm的定轨误差,特别是在径向上。方案2的结果表明,天底角15°~17°部分采用14°的值常数延伸对LEO定轨也有着mm级的影响,主要在径向上;后3种方案的结果之间的差异却很小,初步表明本文方法确实有效且精度良好。为了进一步分析PCV对定轨的影响,将方案1~4的定轨结果与方案5的结果做差,探讨前4种PCV方案的定轨结果与使用IGS公布的0~17°GPS的PCV定轨结果的差异,另外,为了探讨本文所得0~14°部分对LEO定轨的影响,将方案3和4也做了比较,详见图7和表5。

|
| 图 7 各方案所得轨道之间的差异(2012-01-17) Fig. 7 Differences Between the Orbits from the Five Schemes(2012-01-17) |
| (2012-01-16~25)/cm | ||||||||||
| 径向 均值 | 切向 均值 | 法向 均值 | 径向 STD | 切向 STD | 法向 STD | 径向 RMS | 切向 RMS | 法向 RMS | 3D RMS | |
| 方案1~5 | -2.26 | 0.17 | 0.25 | 1.20 | 1.44 | 0.30 | 2.56 | 1.45 | 0.39 | 2.97 |
| 方案2~5 | -1.29 | 0.14 | 0.08 | 0.66 | 0.93 | 0.24 | 1.45 | 0.94 | 0.26 | 1.75 |
| 方案3~5 | -0.23 | -0.01 | 0.03 | 0.11 | 0.15 | 0.06 | 0.25 | 0.15 | 0.07 | 0.30 |
| 方案4~5 | -0.23 | -0.02 | 0.04 | 0.10 | 0.13 | 0.05 | 0.25 | 0.13 | 0.07 | 0.29 |
| 方案3~4 | 0.01 | 0.01 | 0.00 | 0.07 | 0.12 | 0.05 | 0.07 | 0.12 | 0.05 | 0.14 |
由图7和表5可以看出,方案1~5的结果反映出,导航卫星发射天线PCV对LEO定轨的影响主要集中在径向和切向上,径向上均值和标准差会有1 cm~2.5 cm左右的偏差,切向上标准差有1 cm~1.5 cm的差异;方案2~5的结果表明常数延伸PCV得到的定轨结果相对方案1有较大改善,但是依然存在约1.3 cm的偏差,这也表明15~17°部分的PCV对JASON-2精密定轨有着较大的影响;方案3~5和方案4~5的结果反映出,本文所得PCV与IGS的PCV在JASON-2精密定轨结果上差异较小,主要在径向上有约2 mm的均值偏差;方案3~4的结果表明本文所得0~14°部分的PCV对JASON-2精密定轨影响小于1 mm。
由此可见,要得到高精度LEO轨道,需要仔细考虑15°~17°部分的PCVs;而基于本文方法解算得到的GPS卫星PCV在天底角0~14°部分,与IGS08.atx中的PCV值相比,符合很好,精度达到1 mm,15°~17°部分也很好,只有IIR-A类卫星略差;基于本文PCV进行JASON-2精密定轨,可以达到3D-RMS约为3 cm,径向优于1 cm的精度,与采用IGS的PCV得到的轨道相比差异在2 mm~3 mm,主要体现在径向上。整体说明此方法确实可行且有效,精度良好。
4 结 语本文尝试了一种基于LEO实测星载GNSS残差建模的方法,利用JASON-2 3个轨道重复周期的数据,估计导航卫星天线相位中心变化,并将天底角成功拓展至17°。与IGS08_1745.atx的PCV差异在1 mm~3 mm。利用本文所得PCV和其他几种方案,探讨了导航卫星PCV对LEO精密定轨的影响,一个独立的轨道重复周期的结果表明PCVs对JASON-2精密定轨有着1 cm~2 cm的影响,定轨中需要认真考虑。基于本文所得PCV的定轨结果3D-RMS约为3 cm,径向精度优于1 cm,与采用IGS的PCV解算的轨道相比差异在2 mm~3 mm。本文方法不受对流层的影响,拓展了天底角范围,且在较短时间即可实现全球覆盖,所得PCV精度良好,可为其他卫星导航系统特别是我国北斗卫星天线相位中心的在轨标定提供有益参考。
| [1] | Gendt G. IGS Switch to Absolute Antenna Model and ITRF2005[R]. IGSMAIL-5438, IGS Central Bureau, Pasadena,2006 |
| [2] | Schmid R, Steigenberger P, Gendt G, et al. Generation of a Consistent Absolute Phase Center Correction Model for GPS Receiver and Satellite Antennas[J]. Journal of Geodesy, 2007,81(12):781-798,doi:10.1007/s00190- 007-0148-y |
| [3] | Ge M, Gendt G. Estimation and Validation of the IGS Absolute Antenna Phase Center Variations[C]. Proc 2004 IGSWorkshop and Symposium, Bern,2005 |
| [4] | Jggi A, Dilssner F,Schmid R,et al. Extension of the GPS Satellite Antenna Patterns to Nadir Angles Beyond 14°[C]. IGS Workshop 2012,Olsztyn, Poland,2012 |
| [5] | Jggi A, Dilssner F,Schimid R,et al.Extension of the GPS Satellite Antenna Patterns Beyond 14°[C]. European Geosciences Union General Assembly 2012, Vienna, Austria,2012 |
| [6] | Khachikyan R. IGS08_1745.atx:Update Including GPS Satellite Antenna PCV Extension[R]. IGSMAIL-6786, IGS Central Bureau, Pasadena,2013 |
| [7] | Haines B, Bar-Sever Y, Bertiger W, et al.One-Centimeter Orbit Determination for Jason-1:New GPS-Based Strategies[J]. Marine Geodesy, 2004,27(1/2):299-318,doi:10.1080/0149041049 0465300 |
| [8] | Dilssner F, Springer T, Flohrer C, Dow J. Estimation of Phase Center Corrections for GLONASS-M Satellite Antennas[J]. Journal of Geodesy, 2010,84 (8):467-480 |
| [9] | Dach R, Schmid R, Schmitz M, et al.Improved Antenna Phase Center Models for GLONASS[J]. GPS Solutions, 2011,15:49-65 |
| [10] | Zhang Xiaohong, Li Pan, Li Xingxing, et al.Influence of Antenna Phase Center Correction Model on Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2011, 36(12):1 470-1 473(张小红,李盼,李星星,等.天线相位中心改正模型对PPP参数估计的影响[J].武汉大学学报·信息科学版, 2011,36(12):1 470-1 473) |
| [11] | Zhu Zhiqin, Li Zhenghang, Liu Wanke. Impact on GPS Data Processing of Changing from Relative Phase Center Correction to Absolute Phase Center Corrections[J]. Geomatics and Information Science of Wuhan University, 2009, 34(11):1 301-1 304(朱智勤,李征航,刘万科.相位中心改正模式的转变对GPS数据处理的影响[J].武汉大学学报·信息科学版, 2009,34(11):1 301-1 304) |
| [12] | Schmid R, Rothacher M. Estimation of Elevation-Dependent Satellite Antenna Phase Center Variations of GPS Satellites[J]. Journal of Geodesy, 2003,77(7/8):440-446 |
| [13] | Guo Jing, Zhao Qile, Li Min, et al. Centimeter Level Orbit Determination for HY2A Using GPS Data[J]. Geomatics and Information Science of Wuhan University, 2013, 38(1):52-55(郭靖,赵齐乐,李敏,等.利用星载GPS观测数据确定海洋2A卫星cm级精密轨道[J]. 武汉大学学报·信息科学版, 2013,38(1):52-55) |
| [14] | Li Xiaobo, Wang Xiaoya, Ren Jinwei.Research on Calibration Methods of GNSS Antenna Phase Center Offsets and Variations[J]. Progress in Astronomy, 2012,30(4):501-517(李晓波,王小亚,任金卫.GNSS天线相位中心偏差与变化精确标定方法研究[J].天文学进展,2012,30(4):501-517) |
 2015, Vol. 40
2015, Vol. 40


