文章信息
- 李广春, 戴吾蛟, 杨国祥, 刘斌
- LI Guangchun, DAI Wujiao, YANG Guoxiang, LIU Bin
- 时空自回归模型在大坝变形分析中的应用
- Application of Space-Time Auto-Regressive Model in Dam Deformation Analysis
- 武汉大学学报·信息科学版, 2015, 40(7): 877-881
- Geomatics and Information Science of Wuhan University, 2015, 40(7): 877-881
- http://dx.doi.org/10.13203/j.whugis20130549
-
文章历史
- 收稿日期:2013-10-08
2. 湖南省精密工程测量与形变灾害监测重点实验室, 湖南 长沙, 41008;
3. 五凌电力有限公司, 湖南 长沙, 410004
2. Key Lab. of Precise Engineering Surveying & Deformation Disaster Monitoring of Hunan Province, Changsha 410083, China;
3. Wuling Power Corporation, Changsha 410004, China
变形分析是大坝安全监测的主要工作,它是通过对变形监测数据的整理和分析,发掘变形体的时空特性及变形规律,并建立相关模型对变形体的发展态势进行预测、预警和预报[1]。时间序列及系统分析理论具有预测复杂系统发展趋势的能力,用自回归模型可描述变形体的变形趋势并进行预报预测[2, 3]。在传统的大坝变形分析建模的过程中,通常对单个测点的位移监测序列进行建模,这意味着需要对所有的测点进行建模,造成大量模型冗余。而实际上,大坝变形监测数据之间不仅存在时间相关性,而且大坝作为一个整体结构,各监测点之间的位移是相互关联的,即存在空间相关性,因此,针对单测点的变形模型不利于大坝变形的整体分析。
时空自回归模型(space-time auto-regressive,STAR)是根据时空序列的时间相关性和空间相关性对序列进行分析的一种建模方法,是对随机变量内部的相关关系进行分析。考虑观测点之间相关联的信息,对空间多点的整体变形进行分析与预报,有可能实现变形分析的较大突破[4]。本文利用时空自回归模型对五强溪大坝一条引张线上的多个测点的水平位移序列数据进行建模,并与单点的时间自回归模型进行对比分析,探讨其在大坝整体变形分析中的实际应用效果。
1 时空自回归模型对于平稳的时空序列,其时空自回归滑动平均(STARMA)模型的一般形式为[5]:
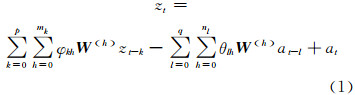
式中,at为随机误差,服从正态分布;p、q分别为时间自回归和滑动平均阶数;mk、nk分别为时间延迟k时的空间自回归和滑动平均阶数;W(h)为h阶空间延迟的权阵,表示空间上的h阶邻接,W(0)=E。权重矩阵一般在建立模型时给出。
本文主要讨论空间阶数不随时间阶p变化的时空自回归模型:
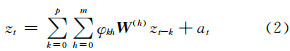
空间权重矩阵是反映空间相邻点之间的影响大小,对于分布较规则的区域,空间权重矩阵一般根据空间的邻近性确定,即与目标点相邻的点对应的元素为1,其他的对应元素为零。
由于每一个空间点的相邻点的个数不同,导致空间权阵的影响不一致,为确保每个点空间相邻点的总影响是一致的。对空间权阵进行标准化处理:

式中,ωij为标准化前空间权阵的第i行第j列的元素;ωi.为空间权阵的第i行的元素之和;Wij为标准化后的空间权阵元素。
时空序列建模的主要过程如下[6]。
1)模式识别。通过自相关系数和偏自相关系数的截尾性确定模型的类型。确定模型阶数常用的方法是残差平方和准则、白噪声检验准则、Akaike信息准则[7]和F-准则等。残差平方和准则通过高阶模型的残差平方和是否明显低于低阶模型为标准,没有明确的衡量标准,而且确定的模型阶数一般较高[7];白噪声检验准则,由于样本的局限,残差的统计量存在一定的不确定性[8];F-准则,当两个比较模型均不适用时F-准则不能给出判断;Akaike信息准则考虑了模型阶数的增加,可能使计算更加复杂,计算误差也会较大。其中,应用较广泛的Akaike信息准则有:
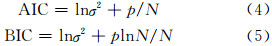
式中,σ2为残差的方差;p是模型的阶数;N为数据长度。理论已经证明,AIC确定的阶数并不是其真值的一致性估计;BIC更多地考虑了模型的阶数,也是模型阶数真值的一致性估计[8],本文选用BIC用以确定模型的阶数;
2)参数估计。时空自回归模型参数估计中常用的方法有最小二乘法和极大似然估计法。极大似然估计计算0阶时间延迟对应系数时,需求似然函数二阶导[9]计算较复杂。本文采用最小二乘估计。
3)模型检验[10]。检验所建立的模型是否适用,并对参数进行检验。通过构造模型的整体统计量:
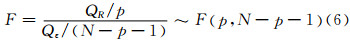
式中,N为样本长度;p为参数的个数。一般给定F-检验的显著水平ɑ为0.05,对模型进行总体的显著性检验。F-检验只能说明模型在总体上是显著的,但并不能够保证模型的每一个参数都是显著的,因此,还需要对每一个参数进行显著性检验。通过构建统计量:

式中,qi为参数φi的协因数;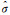 为方差。可以通过T-检验对每个参数的显著性进行检验,从而来确定最后的时空自回归模型;可以根据建立的模型对时空序列进行预测。
为方差。可以通过T-检验对每个参数的显著性进行检验,从而来确定最后的时空自回归模型;可以根据建立的模型对时空序列进行预测。
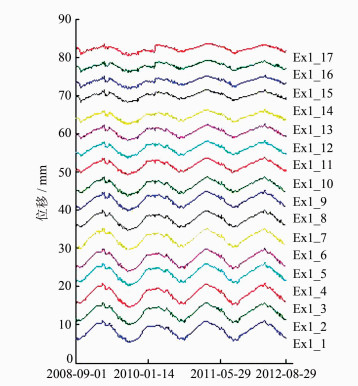
五强溪大坝位于湖南省沅陵县境内的沅水干流上,为混凝重力坝,最大坝高85.8 m,最大底宽68 m,正常蓄水位108 m时,总库容42.9亿 m3。大坝装有引张线、倒铅锤、静力水准、渗流监测、浮力监测、水位测量等自动监测系统。本文收集了2008-09-01~2012-08-28五强溪大坝坝顶引张线上17个测点的位移监测数据,数据采样率为1 d(实为1 d位移的均值)(图 1),为便于比较各测点的时间序列,将各点的数据逐次加同一常数5。
|
| 图 1 原始观测值 Fig. 1 Original Observations |
为了对模型的空间预测能力进行检验,建模时只选择坝顶引张线中的16个测点数据参与建模,其中第8号点不参与建模,用于模型空间预测精度的检验。具体建模过程如下。
(1)数据预处理。利用3倍中误差法对含有粗差的数据进行剔除,然后利用拉格朗日插值法插补缺失的数据。
(2)平稳化位移数据序列经过分析发现,所有测点位移序列都存在明显的年周期项,为平稳化数据序列,采用式(8)拟合年周期项:
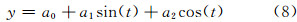
然后从数据序列中扣除年周期项。
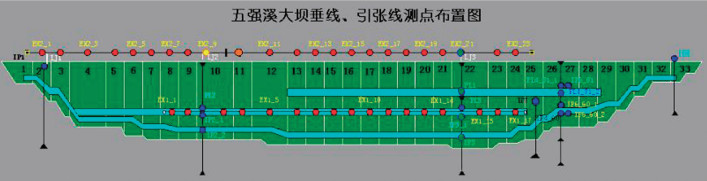
(3)确定空间权重矩阵。张线上相邻监测点的分布较为均匀(图 2),因此,直接利用空间上的邻接性建立空间权阵,在实验中,先建立前3阶的空间权阵。由于边点的存在,对空间权阵 W 进行标准化处理。
(4)模型识别。选取2008-09-01~2011-09-01经平稳化的数据序列,计算3阶空间延迟和6阶时间延迟的时空自相关系数(表 1)和偏相关系数(表 2)。由表 1中的自相关系数和表 2中的偏自相关系数,可知偏自相关系数存在截尾性,适合建立时空自相关模型。
|
| 图 2 引张线测点分布(EX1_1-EX1_17) Fig. 2 Distribution of Measuring Points |
| 时延k/空延h | 0 | 1 | 2 | 3 |
| 1 | 0.980 2 | 0.949 8 | 0.958 3 | 0.923 8 |
| 2 | 0.954 1 | 0.924 1 | 0.932 8 | 0.899 1 |
| 3 | 0.925 1 | 0.895 5 | 0.904 4 | 0.871 4 |
| 4 | 0.894 8 | 0.865 7 | 0.874 6 | 0.842 2 |
| 5 | 0.866 0 | 0.837 3 | 0.846 1 | 0.814 2 |
| 6 | 0.838 3 | 0.809 6 | 0.818 4 | 0.786 7 |
| 时延k/空延h | 0 | 1 | 2 | 3 |
| 1 | 0.980 2 | -0.784 8 | -0.395 9 | -0.135 9 |
| 2 | -0.170 5 | -0.349 2 | -0.118 6 | 0.077 5 |
| 3 | -0.063 3 | -0.140 2 | -0.034 1 | 0.084 3 |
| 4 | -0.032 2 | -0.010 4 | -0.019 6 | 0.036 3 |
| 5 | 0.037 1 | -0.025 8 | -0.042 6 | 0.018 2 |
| 6 | 0.001 3 | -0.092 2 | -0.036 6 | 0.016 4 |
表 3为计算的BIC值,可以看出,在空间延迟为2、时间延迟为2之后BIC的值趋于稳定,因此,可建立STAR(2,1)模型,具体如式(9)所示。
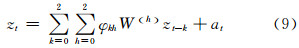
| 时延k/空延h | 0 | 1 | 2 | 3 |
| 1 | -5.380 1 | -6.403 2 | -6.777 6 | -6.815 5 |
| 2 | -5.418 0 | -6.547 7 | -6.903 2 | -6.916 6 |
| 3 | -5.421 2 | -6.578 8 | -6.925 9 | -6.931 4 |
| 4 | -5.420 9 | -6.577 9 | -6.924 1 | -6.927 7 |
| 5 | -5.424 5 | -6.582 6 | -6.928 1 | -6.930 6 |
| 6 | -5.423 8 | -6.592 9 | -6.936 2 | -6.936 9 |
| φ10 | φ21 | φ10 | φ11 | |
| 估计值 | 0.209 | 0.738 | 0.612 | -0.067 |
| T检验 | 29.047 | 102.050 | 85.865 | -8.224 |
| P值 | 0 | 0 | 0 | 0 |
| φ12 | φ20 | φ21 | φ22 | |
| 估计值 | -0.456 | 0.329 | -0.122 | -0.244 |
| T检验 | -45.304 | 46.259 | -17.034 | -26.934 |
| P值 | 0 | 0 | 0 | 0 |
5) 参数估计及模型检验。利用平稳化的数据序列,对模型(9)进行最小二乘估计,模型通过了F-检验后,对每个模型的参数进行T-检验,结果见表 4。由表 4可见所有参数的P值均为0,明显小于给定的显著性水平0.05,故所有参数均通过T检验。最终的时空自回归模型为:
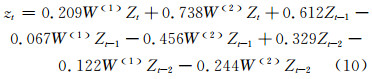
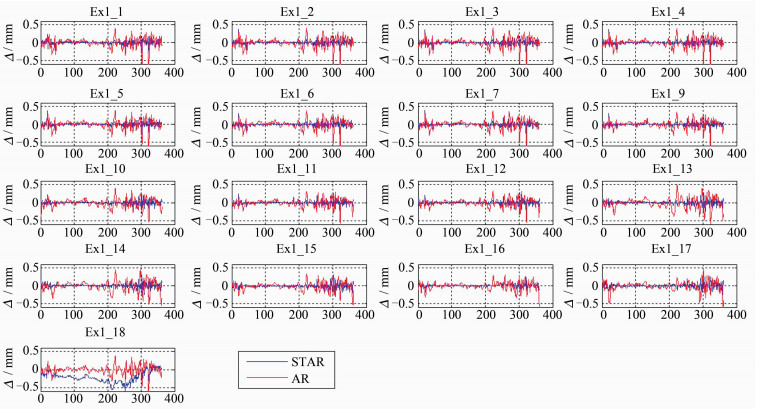
利用已建立的大坝时空自回归模型对引张线上每个测点进行拟合和预测,对2011-09-01~2012-08-28的362 d进行了预测。为了进行比较,对每一测点的位移数据序列建立了单点的自回归模型。选择拟合数据序列与观测数据序列的相关系数(拟合相关系数)、拟合残差数据序列的RMS值(拟合RMS)、预测数据序列与观测数据序列的相关系数(预测相关系数)、预测残差数据序列的RMS值(预测RMS)等4个指标对时空自回归模型和单点自回归模型进行对比分析,结果如表 5所示。图 3为用两种模型往后预测的残差序列对比图。
|
| 图 3 拟合点和检核点(Ex1_8)的预测残差图 Fig. 3 Fitting Point and Check Point (Ex1_8) Prediction Residual Plots |
| 拟合相 关数 | 拟合 RMS | 预测 相关数 | 预测 RMS | |
| STAR | 0.997 | 0.030 | 0.965 | 0.071 |
| AR | 0.987 | 0.066 | 0.915 | 0.131 |
| Ex1_8(STAR) | 0.856 | 0.256 |
从表 5和图 3的对比分析结果可以看出,时空模型在拟合和预测精度上略优于单点自回归模型。Ex1_8点未参与时空自回归模型的建立,其预测精度与其他点的精度相比略差,但还是能够对其进行预测,说明时空自回归模型可以预测坝体上未设立监测点位置的变形,即时空自回归模型不仅具有时间预测能力,而且还具有一定的空间预测能力,这一优势是单点自回归模型无法比拟的。
3 结语时空自回归模型在时间自回归的基础上考虑了同一变形体上不同监测点之间的空间相关性,可以更好地反映时空数据序列的数据结构特征。基于时空自回归模型的五强溪大坝水平方向的变形分析建模结果表明,时空自回归模型在拟合和预测精度方面都与单点模型大致相当,但时空自回归模型还具有空间预测能力,而且无论大坝监测点有多少,整个大坝只需建立一个模型。因此,时空自回归是一种有效的大坝整体变形建模方法,在变形分析中极具应用潜力。
| [1] | Huang Shengxiang, Yin Hui, Jiang Zheng. Deformation Monitoring Data Processin[M]. Wuhan: Wuhan University Press, 2010(黄声享,尹晖,蒋征.变形监测数据处理[M].武汉:武汉大学出版社,2010) |
| [2] | Shang Yuequan, Sun Hongyue, Zhao Fusheng. ARMA Model Analysis of Landslide Deformation[J].Chinese Journal of Geotechnical Engineering, 2000,22(5):628-629(尚岳全,孙红月,赵福生.滑坡变形动态的自回归模型分析[J].岩土工程学报,2000,22(5):628-629) |
| [3] | Chen Yongqi, Wu Zi’an, Wu Zhongru. Deformation Monitoring Analysis and Prediction[M]. Beijing:Surveying and Mapping Press,2003(陈永奇,吴子安,吴中如.变形监测分析与预报[M].北京:测绘出版社,2003) |
| [4] | Yin Hui. Review of the Method to Deformation Analysis and Prediction[J]. Northeast Surveying and Mapping, 2000,23(1):10-13(尹晖.变形分析与预报方法综述[J].东北测绘,2000,23(1):10-13) |
| [5] | Wang Jiaqiu, Deng Min, Cheng Tao, et al. Space-Time Series Data Analysis and Modeling[M]. Beijing: Beijing Scientific Press,2012(王佳璆,邓敏,程涛,等.时空序列数据分析和建模[M].北京:科学出版社,2012) |
| [6] | Wutsqa D U, Suhartono, Sutijio B. Generalized Space-Time Autoregressive Modeling[C]. ICMSA2010, Kuala Lumpur, 2010 |
| [7] | Wu Chao, Lu Chao, Han Yingduo,et al. Low-frequency Oscillation Mode Noise-Signal Recognition with Model Ordering[J].Automation of Electric Power Systems, 2009,33(21):1-5(吴超,陆超,韩英铎,等.计及模型定阶的低频震荡模式类噪声信号识别[J]. 电力系统自动化,2009,33(21):1-5) |
| [8] | Yang Shuzi, Wu Ya, Xuan Jianping. Time Series Analysis in Engineering Application (Second Edition)[M]. Wuhan: Huazhong University of Science & Technology Press, 2007(杨叔子,吴雅,轩建平.时间序列分析的工程应用(第二版)上册[M].武汉:华中科技大学出版社,2007) |
| [9] | Terzi S. Maximum Likelihood Estimation of a Generalized Star(P;L) Model[J]. Ital Static Soc,1995:377-393 |
| [10] | Liu Dajie, Tao Benzao. Practical Methods for Surveying Data Processing[M]. Beijing: Surveying and Mapping Press,2000(刘大杰,陶本藻.实用测量数据处理方法[M].北京:测绘出版社,2000) |
 2015, Vol. 40
2015, Vol. 40



