文章信息
- 汤俊, 姚宜斌, 张良
- TANG Jun, YAO Yibin, ZHANG Liang
- 一种适用于电离层层析成像的TV-MART算法
- A TV-MART Algorithm Applied to Computerized Ionospheric Tomography
- 武汉大学学报·信息科学版, 2015, 40(7): 870-876
- Geomatics and Information Science of Wuhan University, 2015, 40(7): 870-876
- http://dx.doi.org/10.13203/j.whugis20130049
-
文章历史
- 收稿日期:2013-04-15
2. 武汉大学测绘学院, 湖北 武汉, 430079;
3. 东华理工大学江西省数字国土重点实验室, 江西 南昌, 330013;
4. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉, 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. Jiangxi Province Key Laboratory for Digital Land, East China Institute of Technology, Nanchang 330013, China;
4. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China
电离层是日地空间环境的一个重要组成部分,对无线电通讯、卫星导航定位以及人类的空间活动有着重要影响。电离层层析成像(computerized ionospheric tomography,CIT)作为一种空间环境无线电遥测技术的出现,为探测其时空结构开辟了广阔的前景。
1986年,Austen等[1]首次提出利用CT(computerized tomography)技术测量电离层观测剖面内多条路径的总电子含量(total electron content,TEC),重构出剖面中电子密度分布图像。其后电离层层析技术得到了迅速发展,国际上诸多研究者开展了许多实验和理论研究[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]。在实际的电离层层析成像过程中,由于重构区域、卫星轨道以及地面台站之间特定的几何关系,使得采集的投影数据不完备,这是影响重构电离层电子密度分布图像质量的主要因素[4]。现有的电离层层析成像重构算法主要包括迭代算法[1, 2, 3, 4, 5]和非迭代算法[6, 7, 8]两类。迭代算法包括代数重构算法(algebraic reconstruction technique,ART)、乘法代数重构算法(MART)和同时迭代重构算法(simultaneous iteration reconstruction technique,SIRT)等;非迭代算法包括奇异值分解算法以及基于概率论和信息论的重构算法等。近年来,闻德保等[5, 17, 18]、Hobiger等[19]、Garcia等[20]以及Lee等[21]针对电离层层析成像过程中由于投影数据不完备而引起的不适定问题,分别提出了相应的解决方法,有效地克服了重构过程中不适定问题。
目前,应用最广泛的是乘法代数重构算法(multiplicative algebraic reconstruction technique,MART),该算法在投影数据不完备的情况下重构结果较好,然而,对电离层电子密度分布的噪声信息等统计信息考虑欠缺。本质上,电离层层析成像是个典型的病态反演问题,为了避免由噪声引起的不稳定性,本文将总变差(toal variation,TV)最小化算法引入重构过程中,由此提出了一种基于总变差最小化的乘法代数重构算法(TV-MART),并通过实验验证该算法的有效性和可靠性。
1 电离层层析成像模型总电子含量(TEC)是电离层电子密度沿卫星信号传播路径的线积分[2],一般表示为:
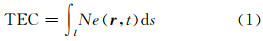
式中,Ne为电离层电子密度;l为卫星信号传播路径;r为t时刻经度、纬度和高度所组成的位置向量。
电离层电子密度与电离层TEC之间是非线性的。在实际反演过程中,为了反演方便,通常采用离散反演方法将待反演的电离层空间离散化。对于离散化的像素基层析反演模型,选取像素指标函数 bj作为基函数,如果射线穿过某像素,则bj为1,否则为0;并将电离层按经度、纬度以及高度方向离散化为三维的格网,其公式表达为:
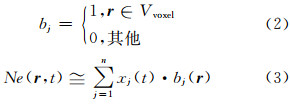
式中,n为离散化的格网数,即总的像素数;xj(j=1,…,n)为模型参数,即离散化后的电离层格网电子密度。那么对每条射线路径上的TEC测量值可以表示为:

式中,m为电离层TEC观测值总数;aij为投影矩阵元素,即第i条射线在第j个格网内的截距。考虑到测量中观测噪声和离散误差的影响,且假定在一定时间段内格网内电子密度是不变的,则每条射线传播路径上的电离层TEC测量数据可表示为:
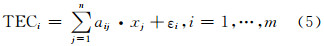
将式(5)用矩阵形式表示为:
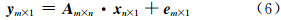
式中,y为电离层TEC观测值组成的m维列向量;A为投影矩阵(射线在对应像素内的截距构成的m个n维的行向量);x为未知参数组成的n维列向量;e为观测噪声和离散误差组成的m维列向量。
2TV-MART算法原理针对离散的电离层电子密度图像,考虑成像数学模型式(6),由于射线只过部分格点,致使 A 为一个大型稀疏矩阵,因此不能直接由 y求出x ,通常将式(6)的求解问题变为一个优化问题。由于直接利用优化方法求解可能会导致数值求解的不稳定,使求解的模型与真实的模型不符。通常对参数进行先验约束,考虑到总变差[22]具有抑制噪声同时能较好地保持图像边缘的优点,可将其作为先验约束引入到电离层层析成像重构建模中,即TV最小化的电离层层析成像模型为:
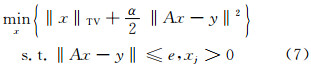
式中,

其中n1、n2和n3分别表示沿经度、纬度和高度方向上的格网数,且离散化的总格网数n=n1×n2×n3;α为正则化参数。
乘法代数重构算法是基于最大熵原理的优化算法[23],利用某一时间、射线不断修正电子密度图像,每一步迭代改进以乘法的形式进行,即有:
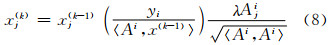
式中,xj(k)为经过k次迭代后第j个格网内的电子密度值;λ为每一步迭代的松弛因子,λ∈(0,1)。
另外,在重构过程中利用先验信息能够有效地改善电子密度图像质量,针对电离层层析成像问题,TV-MART算法的实现步骤如下。
1) 将国际电离层参考模型IRI2007的计算值设为电子密度图像的初值,即 x(0)←IRI2007,设定初始迭代次数为k=1;
2) 利用MART迭代法重构出一幅电子密度图像x(k);
3) 利用总变差约束得到新的电子密度图像:
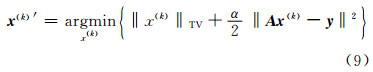
式中,α为正则化参数,通过广义交叉校检准则来确定,本文取α=0.1;
4) 将新的电子密度图像设为迭代初值,进行下一轮迭代,即x(k)←x(k)′,k+1←k。
重复步骤2)~步骤4),直至电子密度值与其前一次值之差充分小或满足迭代次数时,迭代停止。本文选取松弛因子λ=0.2。
3 实验及分析 3.1 模拟数据检验为验证TV-MART算法在电离层层析成像中的有效性,本文采用以下数值模拟的方法进行检验。
1) 实验中选取经度范围为0°E~20°E,纬度范围为45°N~55°N,高度范围为100 km~1 000 km的区域作为测试场景,格网间隔在经度和纬度方向上分别为1°和0.5°,在高度方向上为50 km。
2) 模拟计算中,根据卫星和地面台站位置计算射线在每个像素内的截距,以此来构造式(6)中的投影矩阵 A 。
3) 利用IRI2007电离层模型计算出2011-08-07:13:00UT每个像素内的电子密度,将其与投影矩阵 A 相乘,可得到每一传播路径上的TEC:

4) 由于实际观测中存在噪声误差和离散误差,在实际模拟时,加入一定量的随机误差,则式(10)可写为:
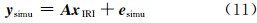
同时,定义平均绝对电子密度误差ρ和标准差σ作为电离层层析成像的精度评定标准:
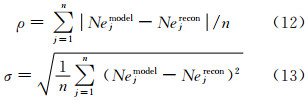
式中,n为待反演的电离层电子密度区域内总像素数;Nejmodel为模型给出的第j个格网的电离层电子密度;Nejrecon为反演的第j个格网的电离层电子密度。
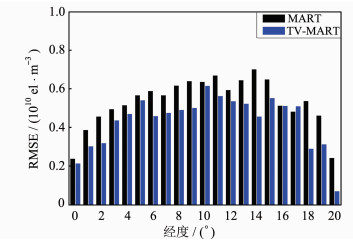
为检验TV-MART算法的重构效果,分别利用TV-MART算法和MART算法进行重构,并进行对比分析。图 1给出了同一时刻不同经度两种算法重构结果的误差比较,从图 1中可以看出,对于不同的经度面,利用TV-MART算法重构的标准差小于MART算法重构电离层电子密度的标准差,这说明该算法的计算精度优于单一的MART算法。表 1列出了两种算法反演结果的误差统计分析,进一步证实了该算法利用模拟的电离层TEC数据,能够以较高的精度重 构电离层电子密度,也从另一侧面反映了TV-MART算法在层析成像中的有效性。
|
| 图 1 不同经度两种算法重构结果误差对比图 Fig. 1 Comparison for Reconstruction RMSE Given by the Two Algorithms at the Different Longitudes |
| 误差 | TV-MART | MART |
| 平均绝对密度误差/(1010el·m-3) | 0.18 | 0.21 |
| 标准差/(1010el·m-3) | 0.45 | 0.54 |
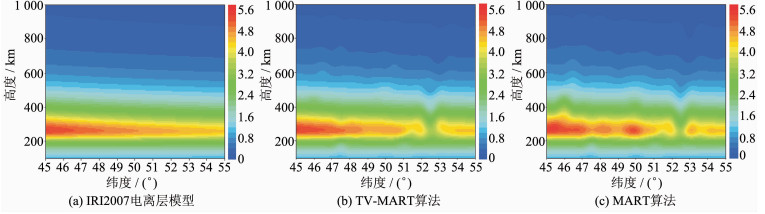
图 2给出了迭代收敛后东经15°子午面上电离层电子密度剖面图。图 2(a)为IRI2007模型给出的结果;图 2(b)为TV-MART算法重构的电子密度分布,其为迭代收敛后17轮迭代结果;图 2(c)为MART算法重构的电子密度分布,其为迭代收敛后24轮迭代结果。可以看出,两种算法重构的电子密度倾斜程度都得到较好的重现,但是,在纬度为52.5°的区域,两者重构的分布图都出现了凹槽现象,这是由于此区域射线扫描很少,从而导致其一定程度的畸变。然而,利用TV-MART重构的电子密度在峰值区更接近于IRI2007模型给出的值,并且在300 km以上,相对于MART算法,利用TV-MART算法重构得到的电子密度的轮廓线抖动更小,进而说明了该算法的重构结果比较稳定。
|
| 图 2 15°E子午面上电离层电子密度剖面图 Fig. 2 The Profiles of IED Given at 15°E |
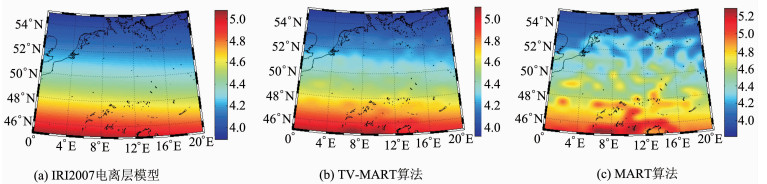
为了进一步检验该算法,展示高度面上的重构效果,图 3给出了迭代收敛后两种算法在300 km高度面上重构的电离层电子密度分布,图 3(a)为IRI2007电离层模型给出的电子密度剖面图;图 3(b)为TV-MART算法重构的电子密度分布;图 3(c)为MART算法重构的电子密度分布。从图 3中可以看出,相对于MART算法,TV-MART算法重构的结果更接近于IRI2007模型模拟的结果,从而进一步证实了该算法的优越性。
|
| 图 3 300 km高度面上电离层电子密度剖面图 Fig. 3 The Profiles of IEDGiven at the Height of 300 km |
以上结论是基于模拟的TEC数据得出的。然而,电离层空间变化极其复杂,Liu等[24, 25]论证了电离层空间变化密切依赖于太阳活动、季节变化和经纬度变化。为了进一步验证TV-MART算法的可靠性,选择2011-08-07:05:00UT、13:00UT和21:00UT等3个不同时刻进行验证。本文采用的观测数据来自欧洲地区IGS观测网络,选取重构区域内的台站观测信息进行重构,并利用两个垂直探测站Dourbes(4.60°E,50.10°N)和Pruhonice(14.60°E,50.00°N)的观测数据进行独立检核。测站分布如图 4所示。
|
| 图 4 欧洲IGS观测站和垂直探测站分布图 Fig. 4 Map of European IGS Observation Stations and Ionosondes |
在利用实测数据重构电离层电子密度之前,首先按照一定的分辨率将待重构的电离层空间离散成一组三维格网,在经度和纬度方向上分别为1°和0.5°,高度方向上为50 km。利用IRI2007模型初始化待重构区域内的每个像素,然后利用实测数据获得的信号传播路径上TEC值进行迭代计算,逐步修正格网内的电子密度,最终得到待重构区域内电子密度的精确结果。
图 5给出了利用实测数据两种算法在同一时刻13:00 UT不同经度重构结果的误差比较,可以看出,利用TV-MART算法反演电离层电子密度的标准差小于MART算法反演电离层电子密度的标准差,该算法的平均绝对密度误差和标准差分别为0.22×1010el/m3和0.84×1010el/m3,而MART算法的平均绝对密度误差和标准差分 别为0.33×1010el/m3和1.09×1010el/m3。根据上述分析结果可以看出,利用TV-MART算法重构电离层电子密度的精度优于MART算法。表 2列出了两种算法在在同一时刻13:00 UT不 同高度面内重构电子密度误差,可以看出,在高度面上TV-MART算法的重构精度优于MART算法,从而进一步证实了该算法的优越性。

|
| 图 5 不同经度两种算法重构结果误差对比图 Fig. 5 Comparison for Reconstruction RMSE Given by the Two Algorithms at the Different Longitudes |
| 高度/km | TV-MART | MART | ||
| 平均绝对密度误差/(109el·m-3) | 标准差/(1010el·m-3) | 平均绝对密度误差/(109el·m-3) | 标准差/(1010el·m-3) | |
| 100 | 1.75 | 0.56 | 2.50 | 0.70 |
| 200 | 4.96 | 1.42 | 6.91 | 1.70 |
| 300 | 7.11 | 1.79 | 10.09 | 2.29 |
| 400 | 3.38 | 0.84 | 5.36 | 1.20 |
| 500 | 1.64 | 0.40 | 2.79 | 0.57 |
| 600 | 0.96 | 0.22 | 1.51 | 0.30 |
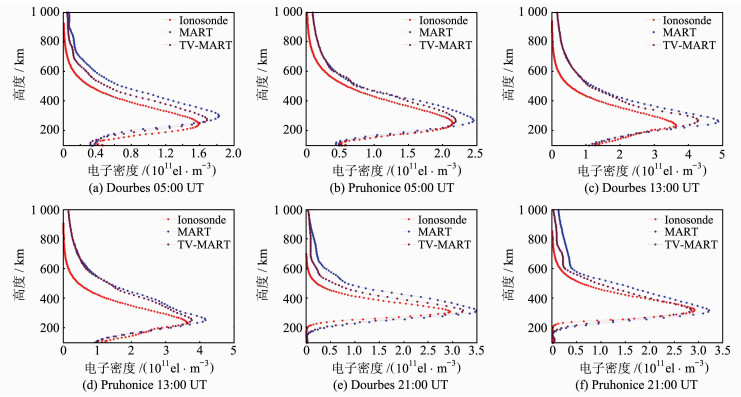
此外,本文利用垂直探测站的观测数据对该算法的电离层层析成像结果进行检核。图 6分别展示了3个不同时刻两个不同站的电离层测高仪所得剖面与两种算法重构结果的比较,图 6(a)、6(c)、6(e)为两种算法重构的电子密度剖面与Dourbes站所得剖面的比较,图 6(b)、6(d)、6(f)为两种算法重构的电子密度剖面与Pruhonice站所得剖面的比较。可以看出,重构获得的F2层电子密度峰值与测高仪观测结果整体上符合的比较好,且改进算法所得结果更加接近测高仪测量结果。然而,F2层的峰值高度与测高仪仍存在一定的差异。由于GPS观测噪声、电离层空间离散化误差及测站几何结构限制等因素,使得反演结果的垂直分辨率仍然需要改善。这说明在电离层层析成像过程中仅仅附加水平和垂直约束来改善电子密度空间结构是不够的,还需要利用其他手段来增加观测信息。
|
| 图 6 两种算法重构电离层电子密度剖面与电离层测高仪测量剖面的对比图 Fig. 6 Comparison of Reconstruction IED Profiles by Two Algorithms with IED Profiles Measured by Ionosondes |
本文针对现有的电离层层析成像模型存在的问题,提出了一种联合TV最小化和乘法代数重构算法的新算法。从数值模拟实验和实测数据两方面证实了该算法在电离层电子密度重构过程中的可行性以及其相对MART算法的优越性,并利用电离层测高仪测量数据进行检核,进一步证实了该算法的可靠性。同时,由于地基GPS对水平分辨率较高,垂直分辨率较低,仅利用算法改正是不够的,需要获取更多的数据信息进行层析成像。
致谢: 感谢IGS提供的观测数据,NASA提供的IRI2007电离层模型数据,SPIDR提供的测高仪数据。
| [1] | Austen J R, Franke S J, Liu C H. Ionospheric Imaging Using Computerized Tomography[J]. Radio Science, 1988, 23(3): 299-307 |
| [2] | Raymund T D, Austen J R, Franke S J, et al. Application of Computerized Tomography to the Investigation of Ionospheric Structures[J]. Radio Science, 1990, 25(5): 771-789 |
| [3] | Pryse S E, Kersley L, Mitchell C N, et al. A Comparison of Reconstruction Techniques Used in Ionospheric Tomography[J]. Radio Science, 1998, 33(6): 1 767-1 779 |
| [4] | Wu Xiongbin, Xu Jisheng, Ma Shuying. An Improved Reconstruction Algorithm for Computerized Ionospheric Tomography[J]. Chinese Journal of Geophysics, 43(1): 20-28(吴雄斌, 徐继生, 马淑英. 一种改进的电离层层析成像算法[J]. 地球物理学报, 2000, 43(1): 20-28) |
| [5] | Wen Debao, Liu Sanzhi. A New Ionospheric Tomographic Algorithm-Constrained Multiplicative Algebraic Reconstruction Technique (CMART)[J]. Journal of Earth System Science, 2010, 119(4): 489-496 |
| [6] | Fremouw E J, James A S. Application of Stochastic Inverse Theory to Ionospheric Tomography[J]. Radio Science, 1992, 27(5): 721-732 |
| [7] | Zhou Chucai, Fremouw E J, Sahr J D. Optimal Truncation Criterion for Application of Singular Value Decomposition to Ionospheric Tomography[J]. Radio Science, 1999, 34(1): 155-166 |
| [8] | Bhuyan K, Singh S B, Bhuyan P K. Tomographic Reconstruction of the Ionosphere Using Generalized Singular Value Decomposition[J]. Current Science, 2002, 76(7): 1 117-1 120 |
| [9] | Na H R, Lee H. Resolution Degradation Parameters of Ionospheric Tomography[J]. Radio Science, 1994, 29(1): 115-125 |
| [10] | Andreeva E S, Franke S J, Yeh K C. On Generation of an Assembly of Images in Ionospheric Tomography[J]. Radio Science, 2001, 36(2): 299-309 |
| [11] | Kunitsyn V E, Tereshchenko E D. Radio Tomography of the Ionosphere[J]. IEEE Antenas and Propagation Magazine, 1992, 34(5): 22-32 |
| [12] | Kunisyn V E, Andreeva E S, Razinkov O G. Phase and Phase-Difference Ionospheric Radio Tomography[J]. International Journal of Imaging Systems and Technology, 1994, 5(2): 128-140 |
| [13] | Tsai L C, Liu C H, Tsai W H, et al. Tomographic Imaging of the Ionosphere Using the GPS/MET and NNSS Data[J]. Journal of Atmospheric and Solar Terrestrial Physics, 2002, 64: 2 003-2 011 |
| [14] | Ma X F, Maruyama T, Ma G, Takeda T. Three-Dimensional Ionospheric Tomography Using Observation Data of GPS Ground Receivers and Ionosonde by Neural Network[J]. Journal of Geophysical Research, 2005, 110(A05308), doi: 10. 1029/2004JA010797 |
| [15] | Li Hui, Yuan Yunbin, Yan Wei, et al. A Constrained Ionospheric Tomography Algorithm with Smoothing Method[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4): 412-415(李慧, 袁运斌, 闫伟, 等. 附加平滑约束的电离层层析反演[J]. 武汉大学学报·信息科学版, 2013, 38(4): 412-415) |
| [16] | Wu Han, Yao Yibin, Chen Peng, et al. Investigation of GNSS-Based Ionospheric Tomographic Alforithms[J]. Geomatics and Information Science of Wuhan University, 2013, 38(12): 1 405-1 408(吴寒, 姚宜斌, 陈鹏, 等. GNSS电离层层析成像算法研究[J]. 武汉大学学报·信息科学版, 2013, 38(12): 1 405-1 408) |
| [17] | Wen Debao, Yuan Yunbin, Ou Jikun, et al. A Hybrid Reconstruction Algorithm for 3-D Ionospheric Tomography[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(6): 1 733-1 739 |
| [18] | Wen Debao, Wang Yong, Norman R. A New Two-Step Algorithm for Ionospheric Tomography Solution[J]. GPS Solution, 2012, 16(1): 89-94 |
| [19] | Hobiger T, Kondo T, Koyama Y. Constrained Simultaneous Algebraic Reconstruction Technique (C-SART)——A New and Simple Algorithm Applied to Ionospheric Tomography[J]. Earth Planets Space, 2008, 60(7): 727-735 |
| [20] | Garcia R, Crespon F. Radio Tomography of the Ionosphere: Analysis of an Underdetermined, Ill-Posed Inverse Problem, and Regional Application[J]. Radio Science, 2008, 43(RS2014), doi: 10. 1029/2007RS003714 |
| [21] | Lee J K, Kamalabadi F. GPS-based Radio Tomography with Edge-Preserving Regularization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(1): 312-324 |
| [22] | Vogel C R. Computational Methods for Inverse Problems[M]. Philadephia, PA :SIAM, 2002 |
| [23] | Kunitsyn V E, Tereshchenko E D. Ionospheric Tomography[M]. Berlin, Heidelberg: Springer-Verlag, 2003 |
| [24] | Liu Libo, Wan Weixing, Chen Yiding, et al. Solar Activity Effects of the Ionosphere: A Brief Review[J]. Chinese Science Bulletin, 2011, 56(12): 1 202-1 211 |
| [25] | Liu Libo, Wan Weixing, Chen Yiding, et al. Recent Progresses on Ionospheric Climatology Investigations[J]. Chinese Journal of Space Science, 2012, 32(5): 665-680 |
 2015, Vol. 40
2015, Vol. 40


