文章信息
- 徐振亮, 闫利, 马振玲, 李艳焕, 张毅
- XU Zhenliang, YAN Li, MA Zhenling, LI Yanhuan, ZHANG Yi
- 轴角描述的光束法平差新方法
- A Nevel Bundle Adjustment Method Based on the Axis/Angle Expression
- 武汉大学学报·信息科学版, 2015, 40(7): 865-869
- Geomatics and Information Science of Wuhan University, 2015, 40(7): 865-869
- http://dx.doi.org/10.13203/j.whugis20140176
-
文章历史
- 收稿日期:2014-03-10
2. 辽宁工程技术大学审计处, 辽宁 阜新, 123000
2. Audit Office, Liaoning Technical University, Fuxin 123009, China
光束法平差中,有效、可靠地描述坐标系间的旋转关系是解决快速而可靠解算的一个关键问题。在传统摄影测量中,欧拉角是最常用的影像姿态的描述方法[1, 2]。小面幅近景影像处理中,影像外方位元素数量往往是比较大的,并且定向参数之间存在很强的相关性,这些可能导致法方程严重病态,常规的欧拉角算法此时难以快速稳健解算。此外,欧拉角描述的影像姿态容易出现表达的奇异性和插值不连续等问题,且需进行大量而冗繁的三角函数计算,影响了解算效率和精度。因此,研究有效旋转矩阵描述方法至关重要。
Chasles已证明,刚体运动同样可以通过绕某轴旋转及沿该轴平移得到,也就是说旋转矩阵可以用一个旋转向量和旋转角来描述,这就是所谓的轴角(axis/angle)。 文献[3]指出,在描述目标姿态方面,轴角法相比欧拉角,具有较好的稳健性,需要较少的状态向量、简洁的建模能力及良好的插值效果;相比四元数,轴角法利用3个独立参数描述空间姿态,为一组最小姿态实现[4],即轴角方式描述姿态是无冗余的,因此,在机器人关节运动学中有着广泛应用[5, 6, 7],但一直没有引起摄影测量与遥感学界的关注。
本文首先回顾轴角法描述姿态及旋转的相关数学理论,然后推导出轴角法描述共线方程的线性化形式,建立基于轴角法的光束法平差方法,最后通过实测数据验证方法的正确性与有效性。
1 轴角描述的旋转矩阵 1.1 Rodrigues定理摄影测量中,像空间坐标(x,y,-f)与像空间辅助坐标(X,Y,Z)有如下关系:

式中,R为像空间坐标系至像空间辅助坐标系的旋转矩阵,描述了影像像空间坐标系在像空间辅助坐标系的姿态,R可以用一个旋转向量和一个旋转角(轴角)来刻画,如图 1所示。

|
| 图 1 轴角法姿态描述 Fig. 1 Description the Attitude Angle/Axis Method |
轴角描述的旋转矩阵R是旋转向量l=[l1 l2 l3]T对 应的反对称矩阵的指数函数[8, 9],即

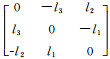 ;θ为旋转角,等于l的模(即θ=‖l‖),这就是Rodrigues定理。式(2)同样可以表达为:
;θ为旋转角,等于l的模(即θ=‖l‖),这就是Rodrigues定理。式(2)同样可以表达为:
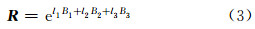
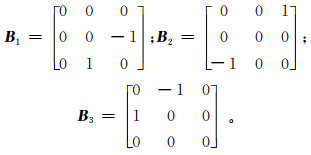
旋转矩阵与旋转向量是可以相互转换的,由旋转向量可以构建旋转矩阵,相反,由旋转矩阵同样可以得到旋转向量[9]:
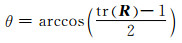
或

式中,tr(·)为矩阵的迹。
2 轴角描述的光束法平差模型 2.1 共线方程的矩阵形式表达摄影测量学中,将同名的物点与像点满足的函数关系描述为共线方程,经典的共线方程经常表达成解析形式,若不顾及检校参数及畸变差,共线方程可表示为:
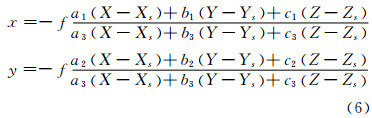
而在计算机视觉领域习惯将上述解析表达式用齐次坐标形式的矩阵形式表示,为了利于采用矩阵分析方法推导平差模型,仿照计算机视觉投影方程表达,再顾及两个学科领域对于旋转矩阵及平移向量定义差异性,共线方程的矩阵方程形式为:
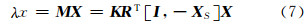
式中,x=[xT,1]T=[x y 1]T、X=(XT,1)T=[X Y Z 1]T分别为像点坐标及物方点坐标的齐次坐标形式;K为由主距构成的对角矩阵,K=diag(-f,-f,1)。
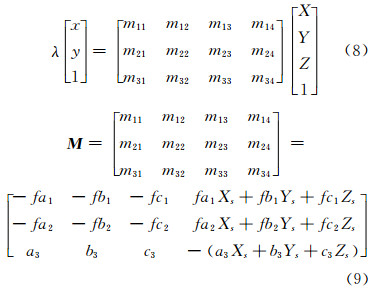
式(9)为投影矩阵的计算公式,结合式(7)~式(9),式(6)可表达为:

式中,[U,V,λ]T为物方点的像空间辅助坐标系坐标。
2.2 轴角描述的平差模型如果将前述中的旋转矩阵R由轴角形式 (Xs,Ys,Zs,l1,l2,l3)来描述,将式(6)线性化处理可得到轴角描述下的像点坐标误差方程式:

式中,a11~a26为共线条件函数对各参数的偏导数。
式(11)可用矩阵表达为:
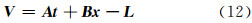
式中,
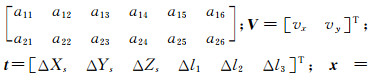
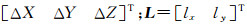 。
。
这里,采用复合函数求导方法(链式法则)推导投影函数对外方位元素的导数:

由(10)式,易得:
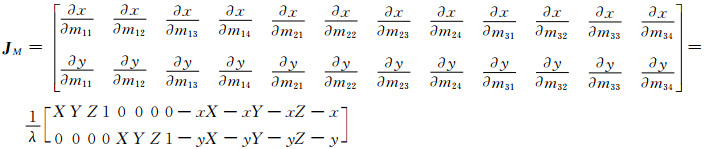
为求Je,对投影矩阵M=KRT[I,-XS]两边对外方位元素求导数
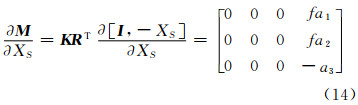
其他变量求导以此类推,
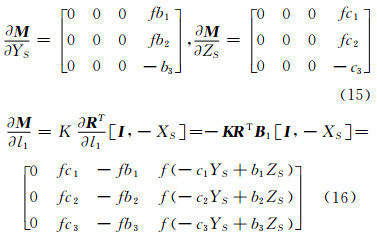
类似地,有:
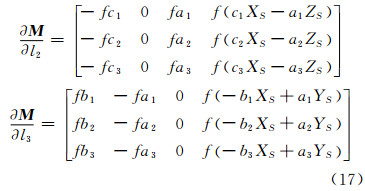
继而可以得到 ,最后可得Je。由式(10)同样易得:
,最后可得Je。由式(10)同样易得:
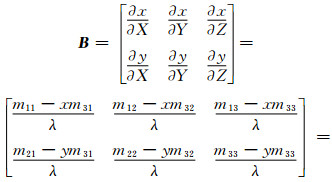
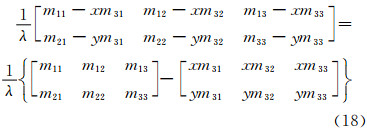
至此,推导出基于轴角描述的线性化共线方程严格模型。
利用轴角描述的平差模型进行迭代解算时,最终的参数估计向量可直接由式(19)给出:
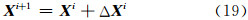
即参数向量姿态部分也可以线性叠加获得新的参数,这是由于R=e[l]×,根据
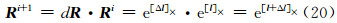
更新的姿态参数为前一次的姿态参数与其增量之和。
计算更新旋转矩阵时,如果旋转向量增量为较小量时,式(2)可由式(21)近似计算:
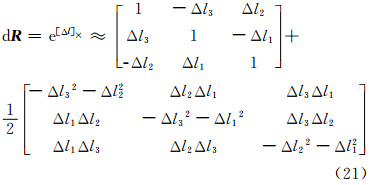
由式(14)、式(18)及式(20)可知轴角描述的光束法平差模型具有以下特点。
1) 经线性化后的共线方程系数皆为投影矩阵及观测值的线性表达式,并且不再具有三角函数关系,这对于迭代计算中提高解算效率有重要意义;
2) 迭代求解中,外方位元素中姿态向量部分可以和位置向量一样直接线性叠加,而在欧拉角描述的姿态模型中,需要将更新后的旋转矩阵分解后获得较精确的参数改正数,带来了大量运算。
3 轴角描述的平差实验与分析分别采用SBA[10]样例中的7张、9张近景影像和10张、50张车载序列影像数据作测试,如表 1所示。测试中使用作者编制的Matlab程序——轴角描述的数字近景影像光束法平差(DCBA3),分别从解算精度及效率两方面验证欧拉角(Eula)与轴角(axis/angle)描述姿态的方法的解算性能,由于没有控制点参与及像点中误差数值较小,精度比较不直观,因此,以像点残差平方和作为衡量两种方法平差精度的指标。
| 实验数据 | 影像景数 | 物方点数 | 像点数 | 最低重叠度 | 最高重叠度 | 初始残差平方和/mm2 |
| 数据1 | 7 | 465 | 1 916 | 3 | 7 | 1.52 755 |
| 数据2 | 9 | 559 | 2 422 | 3 | 9 | 1.12 711 |
| 数据3 | 10 | 1 875 | 7 857 | 3 | 10 | 1.47 603 |
| 数据4 | 50 | 7 418 | 28 214 | 3 | 12 | 1.22 827 |
从表 2一次(单步)解算实验结果来看,轴角法描述的区域网平差在解算效率上明显快于欧拉角描述法,原因在于轴角法没有进行反复三角函数运算,并且至始至终都是采用矩阵运算方式,而欧拉角采用包含三角函数在内的代数解析方法。一次解算后轴角法平差后残差略大与欧拉角法,说明其收敛步长较小。表 3为最终迭代结果。
| 实验数据 | 欧拉角 | 轴角 | ||
| 计算时间/s | 残差平方和/mm2 | 计算时间/s | 残差平方和/mm2 | |
| 数据1 | 0.637 141 | 0.329 592 | 0.355 499 | 0.371 475 |
| 数据2 | 0.623 066 | 0.333 334 | 0.332 608 | 0.353 176 |
| 数据3 | 4.425 745 | 0.219 215 | 1.737 607 | 0.365 051 |
| 数据4 | 57.397 156 | 0.748 176 | 10.479 714 | 0.943 557 |
| 实验数据 | 欧拉角 | 轴角 | ||||
| 计算时间/s | 迭代次数 | 残差平方和/mm2 | 计算时间/s | 迭代次数 | 残差平方和/mm2 | |
| 数据1 | 9.13 | 19 | 0.309 76 | 5.63 | 23 | 0.309 613 |
| 数据2 | 11.72 | 50 | 0.332 596 | 6.10 | 54 | 0.331 811 |
| 数据3 | 124.33 | 10 | 0.196 795 | 91.84 | 19 | 0.194 392 |
| 数据4 | 751.47 | 19 | 0.631 863 | 388.357 542 | 58 | 0.631 567 |
从最终平差结果中不难看出,虽然轴角法迭代次数偏多,但总体计算时间较少,约为欧拉角的一半,并且解算质量偏好,优势不明显(像点残差中误差相当)。在此仍需指出的是,在Matlab平台下求解规模较大的方程组时,处理能力有限,但不妨碍比较两种方法的有效性。
4 结 语1) 本文借鉴计算机视觉领域投影方程形式,构建了一种共线方程的矩阵表达形式,该形式能较方便地利用矩阵理论分析摄影测量问题。
2) 推导得到一种基于轴角描述的光束法平差新方法。通过选用轴角描述的旋转矩阵,使得平差模型较传统欧拉角法形式简洁,免去了繁冗的三角函数运算,姿态向量在迭代中也无需进行旋转矩阵相乘再分解运算,减少了运算量。
3) 实验表明,轴角法描述的光束法平差模型单步收敛步长较小,迭代次数较多,但由于采用线性运算,最终解算速度快于欧拉角描述的平差模型,平差精度与欧拉角法相当,证明方法是正确而可行的,为外方位元素众多的小面幅近景(如车载)影像处理提供了一种崭新的处理方法。
目前,轴角描述的光束法平差方法在近景摄影测量光束法快速平差实验中得到了初步验证,下一步,可将该方法在VC++平台下扩展至定向参数更多、更复杂的卫星摄影测量领域进行试验。
| [1] | Wang Zhizhuo. Photogrammetry Principle[M].Beijing: Surveying and Mapping Press, 1980(王之卓. 摄影测量原理[M]. 北京:测绘出版社,1980) |
| [2] | Yuan Xiuxiao. POS-supported Bundle Block Adjustment[J]. Act a Geodaetica et Cart Ographica Sinica, 2008, 37(3): 342-348(袁修孝. POS辅助光束法区域网平差[J].测绘学报, 2008,37(3):342-348) |
| [3] | Grassia F S. Practical Parameterization of Rotations Using the Exponential Map[J].Journal of Graphics Tools, 1998,3(3):29-48 |
| [4] | Goldstein H. Classical Mechanics[M]. MA: Addison-Wesley, 1980 |
| [5] | Diebel J. Representing Attitude: Euler Angles, Quaternions, and Rotation Vectors[D]. Stanford: Stanford University, 2006 |
| [6] | Jain A. Robot and Multibody Dynamics Analysis and Algorithms[M]. NY: Springer-Verlag, 2010 |
| [7] | Corke P. Robotics, Vision and Control[M]. Heidelberg: Springer-Verlag, 2012 |
| [8] | Ma Songde, Zhang Zhengyou. Computer Vision: Theory and Algolithras[M]. Beijing: Sceince Press, 1998(马颂德,张正友.计算机视觉——理论与算法[M].北京:科学出版社,1998) |
| [9] | Wikipedia. Rotation Matrix[OL]. http://en.wikipedia.org/wiki/Rotation matrix, 2013 |
| [10] | Lourakis A, Argyros A. SBA: A Software Package Forgeneric Sparse Bundle Adjustment[J].ACM Transactions on Mathematical Software, 2009, 36(1):1-30 |
| [11] | Hartley R, Zisserman A. Multiple View Geometry in Computer Vision[M]. Cambridge: Cambridge University Press, 2003 |
| [12] | Zhang Zuxun. Digital Photogrammetry and Computer Vision[J].Geomatics and Information Science of Wuhan University, 2004, 29(12):1 035-1 039(张祖勋.数字摄影测量与计算机视觉[J].武汉大学学报\5信息科学版,2004,29(12): 1 035-1 039) |
| [13] | Zhang Yongjun. Visual Inspection Theory and Method Based on Image Sequence[M]. Wuhan: Wuhan University Press, 2008( 张永军.基于序列图像的视觉检测理论与方法[M].武汉:武汉大学出版社, 2008) |
 2015, Vol. 40
2015, Vol. 40



