文章信息
- 张小红, 潘宇明, 左翔, 汪杰
- ZHANG Xiaohong, PAN Yuming, ZUO Xiang, WANG Jie
- 一种改进的抗差Kalman滤波方法在精密单点定位中的应用
- An Improved Robust Kalman Filtering and Its Application in PPP
- 武汉大学学报·信息科学版, 2015, 40(7): 858-864
- Geomatics and Information Science of Wuhan University, 2015, 40(7): 858-864
- http://dx.doi.org/10.13203/j.whugis20130577
-
文章历史
- 收稿日期:2013-10-16
2. 海军工程大学电气工程学院, 湖北 武汉, 430032
2. School of Electrical Engineering, Naval University of Engineering, Wuhan 430032, China
GPS载波相位观测值的精度比伪距观测值的精度高2~3个数量级,GPS高精度定位中必须使用载波相位观测值。在实际观测中,GPS载波相位观测值中不可避免地会存在周跳或粗差,若不进行必要的控制和处理,势必会影响定位结果的精度和可靠性[1, 2, 3]。针对精密单点定位(PPP)中的质量控制问题,目前,已经发展了多种行之有效的处理方法,如TurboEdit周跳探测方法[4]、选权迭代法[5]、多维粗差探测[6]等。从本质上来讲,这些处理方法都通过构造检验统计量来进行判定和探测。过于宽松的判断标准,会导致粗差或异常不能完全被探测并剔除;过于严格的判断标准,则可能导致部分历元的观测值过少,影响解的可靠性。因此,在实际处理中,为保持数据的连续性,减少不必要的重新初始化,充分利用观测值,一般考虑设置一个较为宽松的阈值,以确保绝大部分周跳或粗差能被正确定位。残余的小周跳或粗差,则可通过抗差估计的方法进行控制。
抗差Kalman滤波方法能有效地抑制观测异常,提高滤波的精度和可靠性,同时具有计算效率高,便于自动化处理等特点,是精密单点定位中常用的一种估计策略[7, 8, 9, 10]。其实质是通过构造等价 权对含粗差观测值进行控制,以消除或减弱异常误差对解的影响。对于观测值中的粗差而言,这种方法降低了异常观测值对于参数估计的贡献,能起到较好的改善作用。但是对于相位观测值中未能探测到的小周跳而言,由于没有判断出周跳,其模糊度初值仍使用上一个历元的估值,造成参数估值与其随机模型不适应。尤其是在可用卫星数少的情况下,会严重影响PPP定位解的精度和可靠性。
本文结合大量的数据处理经验,针对PPP定位中未被探测到的小周跳问题,提出了一种改进的抗差Kalman滤波方案,取得了不错的应用效果。
1 改进的抗差Kalman滤波方案Kalman滤波的状态方程和观测方程为:

式中,X k是系统在t(k)时刻的状态向量和观测量; Φ k,k-1为从t(k-1)时刻到t(k)时刻系统状态的一步转移矩阵; w k为系统噪声向量; L k是系统在t(k)时刻的观测量; H k为观测方程的系数阵; v k为观测噪声。
抗差Kalman滤波与标准Kalman滤波在递推形式上完全一致,两者的差异仅体现在观测模型中量测噪声的方差采用等价方差进行替换。目前,常用的等价权函数有丹麦法[11]、Huber法[1],IGG(Ⅰ~Ⅲ)系列方案[12, 13]等。本文采用IGGⅢ方案,其等价权可表示为[13]:
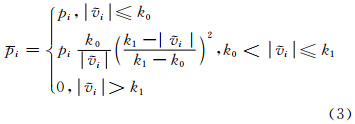
式中,pi为观测量li对应的权; 为标准化残差;k0、k1为常量,一般取k0=1.0~1.5,k1=2.0~3.0。 可以看出,该方案将观测值的权划分为保权区、降权区和拒绝区,通过适当扩大异常观测值的方差以降低异常观测对参数估值的影响。对于含粗差的观测值来说,这种做法是非常有效的。然而,当相位观测值中出现了未能探测到的小周跳时,其对验后观测值残差的影响与粗差类似。当使用传统的抗差估计方案时,只会对观测量进行降权处理,而没有顾及到模糊度参数的变化,导致模糊度参数估值与其方差信息不相容,造成接下来的几个历元继续出现相位观测值残差过大的假象。进而降低了后续历元中正常观测值的贡献,在可用卫星数较少的情况下,可能会严重影响PPP定位解的精度及可靠性。
为标准化残差;k0、k1为常量,一般取k0=1.0~1.5,k1=2.0~3.0。 可以看出,该方案将观测值的权划分为保权区、降权区和拒绝区,通过适当扩大异常观测值的方差以降低异常观测对参数估值的影响。对于含粗差的观测值来说,这种做法是非常有效的。然而,当相位观测值中出现了未能探测到的小周跳时,其对验后观测值残差的影响与粗差类似。当使用传统的抗差估计方案时,只会对观测量进行降权处理,而没有顾及到模糊度参数的变化,导致模糊度参数估值与其方差信息不相容,造成接下来的几个历元继续出现相位观测值残差过大的假象。进而降低了后续历元中正常观测值的贡献,在可用卫星数较少的情况下,可能会严重影响PPP定位解的精度及可靠性。
为此,笔者提出一种改进的抗差估计方案。该方案在原有等价权函数的基础上,对标准化残差大于k1的相位观测值,认为其发生了周跳并重置模糊度参数,而不再对观测值降权;对标准化残差大于k0而小于k1的相位观测值,除对相应的观测值降权外,同时适当扩大其模糊度参数对应的方差,具体放大倍数可根据经验设定(本文取放大两倍)。此外,避免因设计矩阵影响,部分(或单一)粗差被分配到其他正常观测值中,每次抗差迭代时仅对当前验后残差最大的观测量使用等价方差降低其对参数估计的贡献[14]。该方法考虑了模糊度参数和及其方差的一致性,能同时兼顾相位观测值中的粗差和未能探测到的周跳。由于粗差问题通过传统的抗差估计即可较好地控制其影响,故本文只针对载波相位中未被探测到的小周跳情形进行实验分析。
2 实验分析为了验证上述改进方案的有效性,笔者设计了如表 1所示的3种实验方案。方案1联合使用MW (Melbourne-Wübbena)组合和GF(geometry-free)组合进行周跳探测,但对粗差或小周跳现象不做任何处理。方案2、方案3在方案1的基础上分别使用传统的抗差估计和本文提出的改进的抗差估计,可对比分析两种抗差方法处理小周跳问题的效果。
| 方案 | GF | MW | 抗差估计 | 改进的抗差估计 |
| 方案1 | √ | √ | ||
| 方案2 | √ | √ | √ | |
| 方案3 | √ | √ | √ |
实验中所用的IGS观测数据采样间隔均为30 s,周跳探测的阈值[10]取TolMW=2周,TolGF=0.15 m。计算定位结果偏差采用IGS中心发布的测站周解结果作为参考真值。抗差估计仅对相位观测值残差进行检验,且等价权分段阈值取k0=1.0,k1=2.0。下文中如无特别说明,残差均指相位观测值残差。
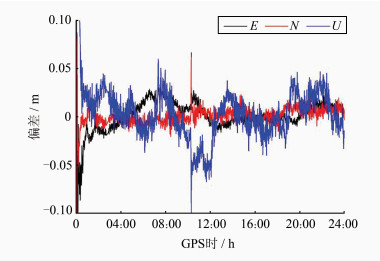
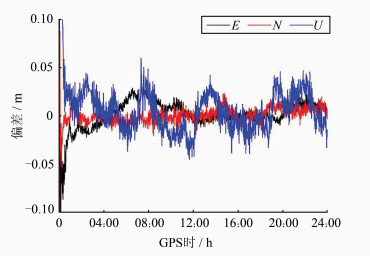
2.1 实测数据实验笔者在处理2011年年积日056天IGS跟踪站ALGO 30 s采样间隔的观测数据时发现,使用方案1进行处理时,从历元10:15:30开始,其定位结果偏差成发散变大趋势,尤其是U方向偏差变化非常明显,如图 1所示。随后检测到G04号卫星在历元10:19:00处发生周跳。这一时段内(10:15:30~10:19:00)GF和MW均没有探测到周跳,也没有可观测卫星更替现象。利用方案2进行处理,结果明显改善,如图 2所示。
|
| 图 1 ALGO站方案1定位结果偏差 Fig. 1 Position Bias of Scheme Ⅰ at ALGO Station |
|
| 图 2 ALGO站方案2定位结果偏差 Fig. 2 Position Bias of Scheme Ⅱ at ALGO Station |
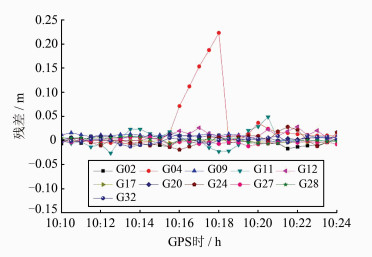
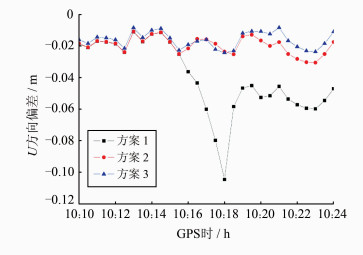
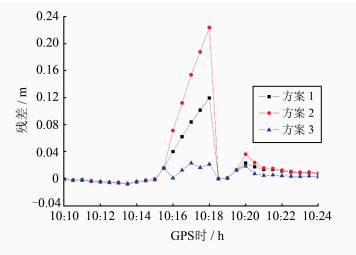
为了更直观地分析该问题,下面仅对10:10:00~10:24:00时段进行考察。通过事后分析相位观测值残差发现,从历元10:15:30开始,各可观测卫星的残差值均呈明显变大趋势,尤其是G04号卫星,如图 3所示。通过残差检验发现,在历元10:16:00时刻,除G04号卫星的标准化残差大于2外,其余卫星标准化残差均小于1。按照方案2的处理策略,认为G04号卫星的相位观测值存在粗差且进行0权处理,方案3则认为此处发生周跳并重置其模糊度。从图 5、图 6中可以看出,虽然方案2明显改善了定位结果,但是接下来的几个历元中出现了G04号卫星残差继续变大的假象,直到下一次发生周跳时才终止。而使用方案3进行处理,在改善定位结果的同时,有效地避免了方案2中出现的问题。

|
| 图 3 方案1中各卫星相位观测值残差 Fig. 3 Satellites’ Phase Residuals of Scheme Ⅰ |
|
| 图 4 方案2中各卫星相位观测值残差 Fig. 4 Satellites’ Phase Residuals of Scheme Ⅱ |
|
| 图 5 各方案U方向定位偏差 Fig. 5 Position Bias in U Direction of Three Schemes |
|
| 图 6 各方案G04号卫星相位观测值残差 Fig. 6 G04's Phase Residuals of Three Schemes |
这说明在历元10:16:00时刻G04卫星出现了未被探测的小周跳而非粗差,按传统抗差方法进行处理虽然能改善定位结果,但会导致后续历元的相位残差继续变大,从而降低正常观测值对参数估计的贡献。但由于实验中的可观测卫星数为9~11颗,只有一颗卫星出现这种情况,因而按方案2处理时该影响并不明显。
2.2 模拟数据实验为了进一步验证该现象的一般性,选取了同一天IGS测站AMC2的观测数据进行模拟周跳实验。选取的模拟周跳组合对于MW和GF探测方法均不敏感,如表 2所示。可以看出,表中的周跳组合均无法被探测到,而其对无电离层模糊度(LC_amb)的影响却非常大。如果不能标记为周跳,必将对定位结果产生显著影响。
| N1/周 | N2/周 | WL/周 | GF/m | LC_amb/m |
| 1 | 1 | 0 | -0.054 | 0.107 |
| 4 | 3 | 1 | 0.029 | 0.805 |
| 5 | 4 | 1 | -0.025 | 0.912 |
| 9 | 7 | 2 | 0.003 | 1.718 |
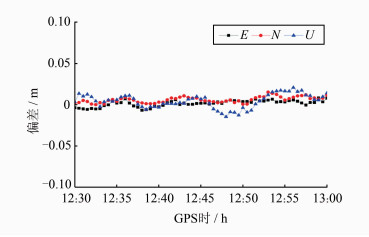
在12:30:00~13:00:00时段内,可用卫星数为7~10颗且均无周跳现象发生。在该时间段人为加入表 2中的周跳组合,然后进行PPP单向动态滤波处理。图 7给出了未加入模拟周跳前该时段的定位偏差,图 8给出了相应的相位观测值残差。在历元12:40:00处(可用卫星数为8颗)分别对各卫星加入表 2中的周跳组合,每次仅对一颗卫星人为加入周跳。限于篇幅,下面仅给出对G04卫星加入(4,3)周跳组合和对G10卫星加入(1,1)周跳组合的结果。
|
| 图 7 加入周跳前的定位偏差 Fig. 7 Position Bias Before Adding Cycle Slips |

|
| 图 8 加入周跳前各卫星的相位观测值残差 Fig. 8 Satellites’ Phase Residuals Before Adding Cycle Slips |
从图 9、图 10可以看出,人为加入GF和MW组合未能探测到的周跳之后,PPP定位结果以及卫星相位观测值残差均受到影响,且模拟周跳组合对无电离层模糊度的影响越大,定位结果越差,残差变化也越大。使用传统抗差后,可显著改善定位结果,但会造成后续历元的相位残差持续超限,从而降低正常观测值对参数估计的贡献。与§2.1中的情况类似,由于可用卫星数较多,该现象对定位结果的影响并不明显。而使用改进后的抗差策略,不但改善定位结果,同时也避免了传统抗差中出现的问题。这验证了§2.1中的相关结论的正确性。

|
| 图 9 G04卫星加入周跳后各方案U方向定位偏差与相位观测值残差 Fig. 9 Position Bias in U Direction and Phase Residuals of Three Schemes After Adding Cycle Slips in G04 |
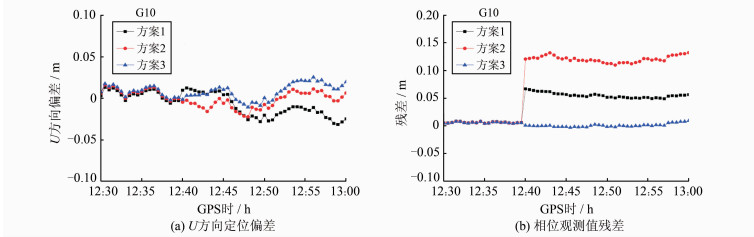
|
| 图 10 G10卫星加入周跳后各方案U方向定位偏差与相位观测值残差 Fig. 10 Position Bias in U Direction and Phase Residuals of Three Schemes After Adding Cycle Slips in G10 |
为了进一步分析方案2在卫星数较少时对定位结果的影响,处理时先禁用G02、G05号卫星,然后进行之前类似的处理。禁用了两颗卫星后,同时段的卫星数及未加周跳前的定位偏差如图 11所示。限于篇幅,同样只给出G04、G10卫星的处理结果,如图 12~图 15所示。

|
| 图 11 加入周跳前的定位偏差及可用卫星数 Fig. 11 Position Bias and Numbers of Valid Satellites Before Adding Cycle Slips |
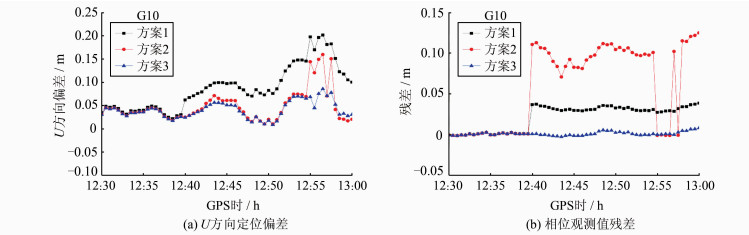
从图 12、图 13可以看出,在可用卫星数较少情况下(5~6颗),方案2对定位结果的改善有 限,甚至可导致定位精度更差。这是由于卫星数较少,异常卫星的相位粗差被分配到其他正常观测值中,使得残差检验判断出错,如图 14、图 15所示。因此,忽略了异常观测值的影响,而对正常观测值进行了错误的降权处理,导致定位结果精度及可靠性降低。同时可看出,较之方案2,由于方案3在一开始就准确定位到了异常卫星,并进行了正确的周跳处理,能明显地改善PPP定位结果,同时避免了传统抗差方法引起的相位残差持续超限,进而影响定位结果的问题。

|
| 图 12 G04卫星加入周跳后各方案U方向定位偏差与相位观测值残差 Fig. 12 Position Bias in U Direction and Phase Residuals of Three Schemes After Adding Cycle Slip in G04 |
|
| 图 13 G10卫星加入周跳后各方案U方向定位偏差与相位观测值残差 Fig. 13 Position Bias in U Direction and Phase Residuals of Three Schemes After Adding Cycle Slip in G10 |

|
| 图 14 G04卫星加入周跳后各卫星相位观测值残差 Fig. 14 Satellites’ Phase Residuals After Adding Cycle Slips in G04 |

|
| 图 15 G10卫星加入周跳后各卫星相位观测值残差 Fig. 15 Satellites' Phase Residuals After Adding Cycle Slips in G10 |
传统抗差估计方案能有效控制观测值中的粗差问题,但对于相位观测值中未能探测到的小周跳情况无法处理。本文提出了一种能兼顾相位观测值中的粗差和小周跳问题的抗差估计方案。实验结果表明,通过对传统抗差估计中相位观测值等价权为0的情况进行周跳处理,不但能改善定位结果,同时可以避免传统抗差方案导致的后续历元相位残差持续增大的问题,具有较好的应用效果。
| [1] | Huber P J. Robust Estimation of a Location Parameter[J]. The Annals of Mathematical Statistics,1964, 35(1): 73-101 |
| [2] | Fang Rongxin, Shi Chuang, Wei Na, et al. Real-time Cycle-slip Detection for Quality Control of GPS Measurements[J]. Geomatics and Information Science of Wuhan University, 2009, 34(9): 1 094-1 097)(方荣新,施闯,魏娜,等. GPS 数据质量控制中实时周跳探测研究[J]. 武汉大学学报·信息科学版, 2009, 34(9): 1 094-1 097) |
| [3] | Cai Hua, Zhao Qile, Sun Hanrong, et al. GNSS Real-time Data Quality Control[J]. Geomatics and Information Science of Wuhan University, 2011, 36(7): 820-824(蔡华,赵齐乐,孙汉荣,等. GNSS 实时数据质量控制[J]. 武汉大学学报·信息科学版, 2011, 36(7): 820-824) |
| [4] | Blewitt G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199-202 |
| [5] | Li Deren. Gross Error Location by Means of the Iteration Method with Variable Weights[J]. Journal of Wuhan Institute of Surveying and Mapping, 1984(1): 46-68 (李德仁. 利用选择权迭代法进行粗差定位[J]. 武汉测绘学院学报,1984(1): 46-68) |
| [6] | Teunissen P J G. Quality Control in Integrated Navigation Systems[J]. IEEE Aerospace and Electronic Systems Magazine,1990, 5(7):35-41 |
| [7] | Zhao Changsheng, Tao Benzao. Robust Kalman Filtering of Linear System with Colored Noises[J]. Geomatics and Information Science of Wuhan University, 2007, 32(10): 880-882)(赵长胜,陶本藻. 有色噪声作用下的抗差卡尔曼滤波[J]. 武汉大学学报·信息科学版,2007, 32(10): 880-882) |
| [8] | Zhang Shuangcheng, Yang Yuanxi, Zhang Qin. An Algorithm of GPS Navigation Based on Robust Self-Tuning Kalman Filtering[J]. Geomatics and Information Science of Wuhan University, 2006, 30(10): 881-884(张双成,杨元喜,张勤. 一种基于抗差自校正 Kalman 滤波的 GPS 导航算法[J]. 武汉大学学报·信息科学版,2006, 30(10): 881-884) |
| [9] | Nie Jianliang, Zhang Shuangcheng, Xu Yongsheng, et al. Precise Point Positioning Based on Robust Kalman Filtering[J]. Journal of Earth Sciences and Environment, 2010(2): 218-220(聂建亮,张双成,徐永胜,等. 基于抗差Kalman滤波的精密单点定位[J]. 地球科学与环境学报,2010(2): 218-220) |
| [10] | Xu Changhui, Gao Jingxiang, Hu Hong, et al. Robust Kalman Filtering for Precise Point Positioning[J]. Journal of China University of Mining & Technology, 2012(5): 857-862(许长辉,高井祥,胡洪,等. 精密单点定位的抗差卡尔曼滤波研究[J]. 中国矿业大学学报,2012(5): 857-862) |
| [11] | Krarup T, Juhl J, Kubik K. Götterdämmerung over Least Squares Adjustment[C]. The 14th Congress of International Archives of Photogrammetry, Hamburg, 1980 |
| [12] | Zhou Jiangwen. The Classical Error Theory and Robust Estimation[J]. Journal of Surveying and Mapping, 1989(2): 115-120(周江文. 经典误差理论与抗差估计[J]. 测绘学报, 1989(2): 115-120) |
| [13] | Yang Yuanxi. Robust Estimation Theory and Its Application[M]. Beijing: People’s Liberation Army Press, 1993(杨元喜. 抗差估计理论及其应用[M]. 北京: 解放军出版杜, 1993) |
| [14] | Zhang Xiaohong, Guo Fei, Li Pan, et al. Real-Time Quality Control Procedure for GNSS Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2012,37(8): 940-944(张小红,郭斐,李盼,等. GNSS精密单点定位中的实时质量控制[J]. 武汉大学学报·信息科学版, 2012,37(8): 940-944) |
 2015, Vol. 40
2015, Vol. 40



