文章信息
- 姚宜斌, 黄书华, 张良, 胡羽丰, 李国平
- YAO Yibin, HUANG Shuhua, ZHANG Liang, HU Yufeng, LI Guoping
- 求解三维坐标转换参数的整体最小二乘新方法
- A New Method of TLS for Solving the Parameters of Three-dimensional Coordinate Transformation
- 武汉大学学报·信息科学版, 2015, 40(7): 853-857
- Geomatics and Information Science of Wuhan University, 2015, 40(7): 853-857
- http://dx.doi.org/10.13203/j.whugis20130302
-
文章历史
- 收稿日期:2013-07-04
2. 成都市勘察测绘研究院, 四川 成都, 610081;
3. 呼和浩特市勘察测绘研究院, 内蒙古 呼和浩特, 010010
2. Chengdu Institute of Survey and Investigation, Chengdu 610081, China;
3. Hothot Prospecting Institute of Surveying and Mapping, Hothot 010010, China
我国已经正式发布并启用了CGCS2000国家大地坐标系[1]。为了将已有的各种测绘成果转换到2000坐标系下,求解出高精度的坐标转换参数就显得尤为重要。如果采用比较通用的布尔莎七参数模型,即认为两个三维坐标系的转换参数包括3个平移参数、3个旋转参数和一个尺度参数,则至少需要已知3个公共点在两不同坐标系下的坐标才可以求出这7个参数。为了求得参数的最佳估值,经典方法常建立高斯-马尔柯夫(Gauss-Markov,G-M)模型利用最小二乘(least-square,LS)法来进行参数的求解[2],由于该方法没有考虑系数矩阵 A 的误差,从统计的观点来看,所求得的参数解不是最优而是有偏的[3]。为了解决这一问题,可以将G\-M模型拓展为系数矩阵含误差(error-in-variables,EIV)的模型,采用整体最小二乘(total-least-squares,TLS)法求解参数值[4]。进一步地考虑到布尔莎7参数模型的系数矩阵 A 的前3列是固定常数值,并不含有误 差,若仍沿用SVD等TLS算法对 A 中所有元素 进行改正则是不合理的,文献[2]提出了LS法与TLS法相结合(LS-TLS)的方法实现对固定列不进行改正。但LS-TLS法中含有误差的一列中仍然存在不含误差的元素(如0元素);其次,系数矩阵中相同元素所求得的改正数却是不同的,这和实际情况是不相符的。
为了解决上述问题,本文提出了一种只对系数矩阵中含有误差的元素进行改正的三维坐标转换参数求解新方法,该方法同时可以使系数矩阵 A 中不同位置的同一元素具有相同的改正数。
1 三维坐标转换的参数求解 1.1 传统LS法求解坐标转换参数设有两个坐标系统分别为 A和B,有一组公共点在两坐标系下的坐标分别为(xAi,yAi,zAi)和(xBi,yBi,zBi),其中i(i≥3)表示公共点的个数。那么,当旋转参数较小时,三维坐标转换7参数模型可表示为[5]:

式中,A∈Rn×t; b ∈Rn×1(n=3i,t=7); (x0,y0,z0)为3个平移参数;μ为尺度参数;(φ,ω,κ)为3个旋转参数。若只考虑观测向量b的误差eb,则可将式(1)表示为线性G-M模型:

那么,以最小二乘准则 e Tb· e b=min求得的参数解为:
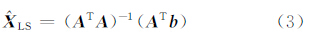
此时观测值的单位权中误差为
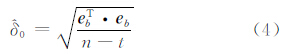
从式(1)可以发现,系数矩阵 A 中的元素(xAi,yAi,zAi)和观测向量 b 中的元素一样是含有误差的,上述最小二乘法并没有考虑系数矩阵 A 中元素的误差 EA ,顾及到这一点可以建立EIV模型
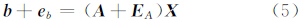
求解该模型的传统方法是由Golub等于1980年提出的奇异值分解(SVD)法[6],在使用该方法求解参数时需要对增广矩阵[A b]进行奇异值的分解:

式中,U ∈ R n×n是左奇异阵; Σ ∈ R n×(t+1)是由特征值组成的对角阵; V ∈ R (t+1)×(t+1)是右奇异阵。当矩阵 V 的第t+1行t+1列元素vt+1,t+1≠0时,利用右奇异阵 V 的最后一列可以表示 出参数的TLS唯一解为:
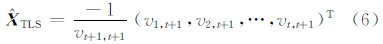
此时变量的单位权中误差为:
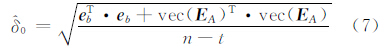
式中,vec(·)表示拉直运算。使用SVD法求解EIV模型是假定系数矩阵的每一个元素都是含有误差的,但这和求解坐标转换参数时的系数矩阵 A 是不相符的。文献[2]提出了一种混合最小二乘法,即把系数矩阵分成 A1、A 2两部分,参数也对应的分成了 X1、X 2两部分。该方法首先对由不含误差的固定列组成的矩阵 A 1进行QR分解,再将 Q左 乘于增广矩阵[A b],则有[2]:

利用 TLS法求出方程 R 22 2= R 2b的解
2= R 2b的解 2,然后将其带入 R 11
2,然后将其带入 R 11 1= R 1b- R 12
1= R 1b- R 12 2中,使用LS法求出
2中,使用LS法求出 1,至此就使用LS-TLS法求得了待求的7个参数,单位权中误差的求解方法和单独使用TLS法是相同的。
1,至此就使用LS-TLS法求得了待求的7个参数,单位权中误差的求解方法和单独使用TLS法是相同的。
针对EIV模型,采用基于SVD方法求解参数时没有顾及到系数矩阵 A 中不同位置的相同元素的改正数不相同。另外,虽然LS-TLS法考虑了系数矩阵中有不含误差的元素,但是只考虑了整列都是固定元素的特殊情况,对于有误差列中的固定元素并没有加以考虑。
1.3 顾及系数矩阵部分元素含有误差的新方法设增广矩阵[A b]中公共点坐标(xAi,yAi,zAi)和(xBi,yBi,zBi)的改正数分别为(ΔxAi,ΔyAi,ΔzAi)、(ΔxBi,ΔyBi,ΔzBi)(i=n/3表示公共点个数),其他固定元素的改正数恒为零,那么,误差矩阵的增广矩阵可以表示为:
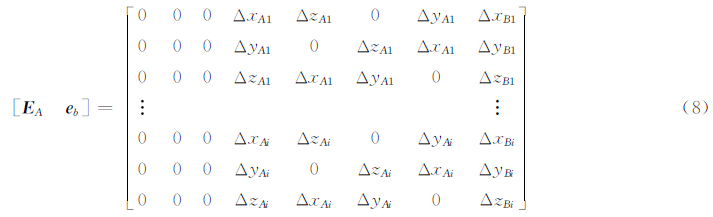
为了使增广误差阵[E A e b]中同一元素具有相同的改正数且只对含有误差的元素进行改正,本文使用的方法是将其中有误差的元素单独取出构成一个新的列向量 Δ ,同时将EIV模型式(5)改写成如下形式:

式中,Δ =[ΔxA1 ΔyA1 ΔzA1 ΔxB1 ΔyB1 ΔzB1… ΔxAi ΔyAi 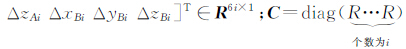 是一个块对角矩阵,其中 R =
是一个块对角矩阵,其中 R = 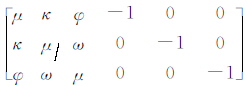 。至此可以得到目标方程:
。至此可以得到目标方程:
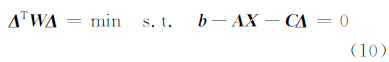
其中对角阵 W ∈ R 6i×6i类似于权阵,其主对角线上的元素依次为 Δ 中对应元素在增广矩阵中出现的次数。此处之所以考虑 Δ 中元素出现的次数是因为在建立7参数坐标转换模型时,同一个观测值出现在了不同的观测方程中,即把同一个观测值当做了多次相同观测参与建模。这样则可以利用式(10)构造出拉格朗日方程:
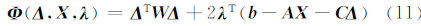
对式(11)中的3个参数分别求导,则有:

可以看出,待求的改正数向量 Δ 中的元素正是系数矩阵 A和观测向量 b 中的元素,矩阵 C 中的元素是由1个尺度参数和3个旋转参数构成的,其初始值是未知的。所以要求得式(12)的稳定解,首先要给矩阵 C 中的未知量赋初值,然后采用迭代法求得。具体的迭代解算步骤归纳如下。
1) 由式(3)采用最小二乘法求得参数的初始解 LS,利用求得的
LS,利用求得的 LS可以构造出矩阵 C 的初始值;
LS可以构造出矩阵 C 的初始值;
2) 将 C 带入到式(12)中,可以求得参数 Δ 和 X 的初始值;
3) 求得参数 Δ 之后,矩阵 A和向量b 加上 Δ 中对应的改正项,重复步骤2)可以求得新的 Δ和 X 的值;
4) 重复步骤2)、步骤3),直至相邻两次求得的 Δ和 X 的值之差小于一个阈值ε为止。
使用上述迭代步骤可以求得参数X的平差值,同时可以得到增广矩阵中各不同元素的改正数 Δ 。本文方法平差模型的自由度为(n+u)-(t+u)=n-t,其中u=3n表示系数矩阵 A 中所含观测量的个数。所以自由度和经典最小二乘是一致的,因此,单位权中误差计算公式为:
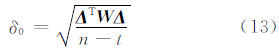
为了验证本文方法的可行性和有效性,选取了某地7个同时具有地方坐标系(A)和WGS\-84坐标系(B)的公共点[7],其在两坐标系下的坐标如表 1所示。
在使用本文方法求解该例的7参数时公共点个数i=7,考虑到增广误差阵(8)中坐标系A中的每个元素都出现3次而坐标系B中的元素仅出现一次,所以对角阵 W= diag(3,3,3,1,1,1,…,3,3,3,1,1,1)∈ R 42×42,块对角阵 C ∈ R 21×42是由7个 R 矩阵构成的。现分别采用不同的方法求取坐标转换参数,其结果见表 2
| 站名 |
|
| 1 | 4 157 222.543 | 664 789.307 | 4 774 952.099 | 4 157 870.237 | 664 818.678 | 4 775 416.524 |
| 2 | 4 149 043.336 | 688 836.443 | 4 778 632.188 | 4 149 691.049 | 688 865.785 | 4 779 096.588 |
| 3 | 4 172 803.511 | 690 340.078 | 4 758 129.701 | 4 173 451.354 | 690 369.375 | 4 758 594.075 |
| 4 | 4 177 148.376 | 642 997.635 | 4 760 764.800 | 4 177 796.064 | 643 026.700 | 4 761 228.899 |
| 5 | 4 137 012.190 | 671 808.029 | 4 791 128.215 | 4 137 659.549 | 671 837.337 | 4 791 592.531 |
| 6 | 4 146 292.729 | 666 952.887 | 4 783 859.856 | 4 146 940.228 | 666 982.151 | 4 784 324.099 |
| 7 | 4 138 759.902 | 702 670.738 | 4 785 552.196 | 4 139 407.506 | 702 700.227 | 4 786 016.645 |
| 参数 | LS法 | SVD法 | LS-TLS法 | 本文方法 |
| x0/m | 641.880 270 | 642.872 790 | 641.880 234 | 641.880 281 |
| y0/m | 68.655 251 | 68.945 177 | 68.655 25 | 68.655 259 |
| z0/m | 416.398 125 | 416.660 162 | 416.398 111 | 416.398 164 |
| μ | 1.000 006 | 1.000 005 | 1.000 006 | 1.000 006 |
| φ/rad | 0.000 004 | 0.000 004 | 0.000 004 | 0.000 004 |
| ω/rad | 0.000 005 | 0.000 005 | 0.000 005 | 0.000 005 |
| κ/rad | -0.000 005 | -0.000 005 | -0.000 005 | -0.000 005 |
从表 2中可以看出,本文方法和LS法、LS-TLS法求得的7参数结果是非常接近的,这说明了本文所提出的方法是可行的。但使用SVD法求得的结果和其他3种方法结果相差较大,这主要是由于系数矩阵 A 中只是部分元素含有误差,而SVD方法仍然以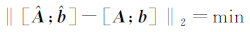 作为平差准则是不完善的[9]。为了证明这一点,可以采用公式
作为平差准则是不完善的[9]。为了证明这一点,可以采用公式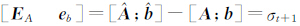
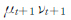 ,求出使用SVD法时的增广矩阵改正数,由于篇幅限制没有写出该矩阵[8]。从求出的改正数可以发现,SVD法对增广矩阵中没有误差的固定元素做了改正,而且不同位置同一元素的改正数是不同的,因此,本文认为在系数矩阵部分元素含有误差采用SVD法求解参数是不可取的。
,求出使用SVD法时的增广矩阵改正数,由于篇幅限制没有写出该矩阵[8]。从求出的改正数可以发现,SVD法对增广矩阵中没有误差的固定元素做了改正,而且不同位置同一元素的改正数是不同的,因此,本文认为在系数矩阵部分元素含有误差采用SVD法求解参数是不可取的。
使用本文方法在求得坐标转换7参数的同时可以求得列向量 Δ,利用求出的Δ 可以构造出增广矩阵的误差阵,限于篇幅该矩阵没有列出来。但从得到的误差阵可以看出,由于本文方法只考虑了系数矩阵中含有误差,所以得到的改正数矩阵只对系数矩阵含有误差的元素进行了改正,并且使得不同位置同一元素具有相同的改正数,这将更加符合实际情况。
3 结 语在使用EIV模型求解小旋转角三维坐标转换的7参数时,由于系数矩阵中有不含有误差的固定项,TLS的传统SVD解法具有理论上的缺陷,求得的参数值是不可靠的。在使用LS-TLS法求解时在理论上有所完善,但是对于有误差列中的固定元素并没有给予特别考虑,也没有考虑到系数矩阵中相同元素改正数不同。本文方法有效地改善了使用EIV模型求解三维坐标转换7参数时存在的缺陷,只针对系数矩阵中含有误差的元素进行改正,并且使得不同位置的同一元素具有相同的改正数。
| [1] | Kong Xiangyuan, GuoJiming, Liu Zongquan. Foundation of Geodesy[M]. Wuhan:Wuhan University Press, 2010(孔祥元,郭际明,刘宗泉. 大地测量学基础[M]. 武汉:武汉大学出版社,2010) |
| [2] | Lu Jue, Chen Yi, Zheng Bo. Applying Total Least Squares to Three-Dimensional Datum Transformation[J]. Journal of Geodesy and Geodynamics, 2008,28(5):77-80(陆珏,陈义,郑波. 总体最小二乘法在三维坐标转换中的应用[J]. 大地测量与地球动力学,2008,28(5):77-80) |
| [3] | Kong Jian, Yao Yibin, Xu Shuang'an. Solving Coordinate Transformation Parameters Based on Total Least Squares Regression[J]. Journal of Geodesy and Geodynamics,2010,30(3):74-78(孔建,姚宜斌,许双安. 整体最小二乘求取坐标转换参数[J]. 大地测量与地球动力学,2010,30(3):74-78) |
| [4] | Zhou Yongjun, Deng Caihua. Extended Total Least Squares Problems for Linear Errors-in-variables Model and Its Typical Applications[J]. The Chinese Journal of Nonferrous Metals, 2012,22(3):948-953(周拥军,邓才华. 线性EIV模型的TLS估计及其典型应用[J]. 中国有色金属学报,2012,22(3):948-953) |
| [5] | Li Jinling, Liu Li, QiaoShubo,et al. Discussion on the Determination of Transformations Parameters of 3D Cartesian Coordinates[J]. Science of Surveying and Mapping 2010,35(4):76-78(李金岭,刘鹂,乔书波,等. 关于三维直角坐标七参数转换模型求解的讨论[J]. 测绘科学,2010,35(4):76-78) |
| [6] | Gloub C, van Loan. An Analysis of the Total Leas-Squares Problem[J]. SIAM J Numer Anal, 1980,17:883-893 |
| [7] | Shen Yunzhong, Chen Yi, Zheng D H. A Quaternion-based Geodetic Datum Transformation Algorithm[J]. J Geod,2006,80:233-239 |
| [8] | van Huffel S,Zha Hongyuan. The Total Least Squares Problem[J]. Elsevier Science Publish B V,1993:377-408 |
| [9] | Akyilmaz O. Total Least Squares Solution of Coordinate Transformation[J]. Survey Review,2007(1):68-80 |
| [10] | Ou Chaomin, Huang Menglong. Design and Implementation of Coordinate Transformation Between Local Coordinate System and CGCS 2000[J]. Bulletion of Surveying and Mapping, 2010(9):26-28(欧朝敏,黄梦龙. 地方坐标系列2000国家大地坐标转换方法研究[J]. 测绘通报,2010(9):26-28) |
| [11] | Chen Yi, Shen Yunzhong, Liu Dajie. A Simplitied Model of Three Dimensional-Datum Transformation Adapted to Big Rotation Angle[J]. Geomatics and Information Science of Whuhan University, 2004, 29(12):1 101-1 105(陈义, 沈云中,刘大杰. 适用于大旋转角的三维基准转换的一种简便模型[J]. 武汉大学学报·信息科学版,2004, 29(12):1 101-1 105) |
| [12] | Lu Tieding, Tao Benzao, Zhou Shijian. Modeling and Algorithm of Linear Regression Based on Total Least Square[J]. Geomatics and Information Science of Whuhan University, 2008, 33(5):504-507(鲁铁定,陶时藻,周世健. 基于整体最小二乘法的线性回归建模和解法[J]. 武汉大学学报·信息科学版,2008, 33(5):504-507) |
| [13] | Lu Tieding, Ning Jinsheng, Zhou Shijian, et al. An Algorithm for Leat-square Collocation by Singular Value Decomposition[J]. Science of Surveying and Mapping, 2008,33(3):47-51(鲁铁定,宁津生,周世健,等. 最小二乘配置的SVD分解解法[J]. 测绘科学,2008,33(3):47-51) |
 2015, Vol. 40
2015, Vol. 40



