文章信息
- 易琳, 袁林旺, 盛业华, 李润超
- YI Lin, YUAN Linwang, SHENG Yehua, LI Runchao
- V-代约束的结构保持空间插值算法
- V-Neighborhood Interation-Constrained Structure-Preserving Spatial Interpolation Method
- 武汉大学学报·信息科学版, 2015, 40(6): 823-828
- Geomatics and Information Science of Wuhan University, 2015, 40(6): 823-828
- http://dx.doi.org/10.13203/j.whugis20130493
-
文章历史
- 收稿日期:2013-09-16
空间插值是空间分析的重要基础[1, 2, 3],空间采样的不均匀性是空间插值算法所面临的关键问题之一[4, 5]。结构保持的空间插值应能兼顾样本空间分布不均与空间结构约束,自适应生成待插控制点并进行估值。常用的空间插值方法多直接基于不规则分布样点进行规则格网插值,易导致样点分布特征的均匀化,进而引起空间结构和统计特征的畸变。如基于距离的插值点估值易出现边缘效应和牛眼现象[4, 6];函数逼近法对数据噪音敏感而出现局部最小[7];地统计学方法基于空间自相关特性进行插值估计和误差不确定性分析,但要求数据分布满足相应的假设条件[8, 9, 10]。因此可从样点空间分布入手,基于样点代表性及分布特征构建几何结构约束的空间插值算法[11, 12]。其策略可归纳为:①根据样本点分布特征生成非均匀的几何空间结构;②构建几何结构约束下的插值控制点生成规则;③建立顾及几何与结构约束的插值控制格网或插值函数。
Voronoi-邻域(简称V-邻域)结构作为一种几何优化结构,可有效表征空间样点分布的结构关系,并能唯一确定不同样点间的空间影响域边界。Voronoi-Delaunay的对偶特性及空间剖分特性提供了样点空间分布范围划分的结构约束规则,可作为兼顾几何结构约束插值点自适应生成的基础[13, 14]。本文基于Voronoi-Delaunay剖分的几何特性作为空间插值的结构约束限定,利用多次迭代Voronoi实现空间影响域逐层划分。基于高阶V-邻域的几何剖分特性,建立基于自然邻域的控制点自适应生成规则及结构约束的空间插值算法。基于中国气象台站日均气温数据进行插值试验,给出了不同层次插值对空间统计量的影响,并与常用插值方法进行了结果对比,讨论了该方法在空间参数特征保持等方面的优势。
1 K层-Voronoi及其插值 1.1 K层-Voronoi设Ω是任意维度空间Rn上的凸空间,给定有限点集S={p1,p2,…,pn}∈Ω,当存在i≠j,pi≠pj 时,则对任意节点x∈S,均可定义一个子空间Vx 满足:
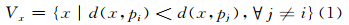
其中,d(pi,pj)为点pi、pj间的欧氏距离;Vx为节点x的一个Voronoi区域。
在点x的Voronoi区域Vx上增加任意新节点y∈Ω,则可生成新的Voronoi区域Vy,此时Vy与原有的点x的Voronoi区域Vx的重叠部分会形成新的Voronoi区域,称之为2层Voronoi区域Vxy[14, 15],数学表达为:
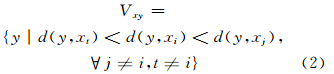
Voronoi的剖分特性表明,对于新的Voronoi区域Vxy自然邻近点坐标可由所划分的新Voronoi区域Vxy的面积与原Voronoi区域Vx的面积比直接确定。更高层次的Voronoi区域同样可由式(2)迭代获得。
1.2 K层-Voronoi插值Voronoi区域的空间剖分特性可为空间插值提供结构性空间约束[16]。对于任意点x,其自然邻近点定义为与它具有共同Voronoi区域边界的节点,即对应Delaunay三角形中与之有连线的节点[17]。自然邻近点定义了几何特性上距离某点最近的节点系,其节点数目和位置仅取决于节点的局部分布,可作为几何结构约束表征的理想控制点。以任意K层-Voronoi的自然邻近点为控制点,基于自然近邻规则[18]的插值定义如下:
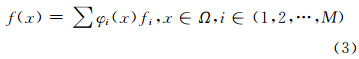
其中,f(x)为待插点x处的插值结果;i是点x的自然邻近点序号;fi为给定的样本点值;φi(x)为对应节点xi的插值基函数。自然邻点插值方法中φi(x)为点x的自然邻近坐标的线性插值,常依据插值前后空间几何剖分的面积比确定。而Voronoi区域的面积大小与节点分布的密度成反比关系,生成单元的疏密程度取决于节点分布的密度[13, 14]。
基于空间分布特征的迭代插值过程如图 1所示。

|
| 图 1 基于空间分布特征的迭代插值过程 Fig. 1 Iterative Interpolation Process Based on Data Spatial Distribution |
以基于原始点生成的K层-Voronoi的自然邻近点作为空间插值的控制点,即基于原始样点构建Delaunay三角网,各三角形的空间范围反映了已知数据的几何分布特征,并作为样点分布的结构约束初始结构。基于Delaunay和Voronoi的对偶关系,将Delaunay三角网中三角形的质心作为下一层Voronoi区域的自然邻近点。以此类推,可逐层生成K层-Voronoi自然邻近点的坐标。Voronoi空间剖分的不规则性导致插值控制点生成的不规则性。在任意K层,原始数据分布 稀疏的区域,三角形的分布个数较少,而分布较密集的地区,生成的待插点相对集中。考虑控制点与插值分辨率的关系,基于Voronoi插值的分辨率由迭代次数控制,而非传统插值算法的单元大小。迭代次数增加时,原始样点密集区插值点增加越多,而稀疏区的插值点增加相对较慢,从而保持对原有空间样本分布结构的表征。
2.2 基于V-邻域的迭代插值规则基于前述K层-Voronoi的定义,可以将每次生成的K层-Voronoi的自然邻近点作为φi(x)的基础构建插值方法。由于反距离加权函数空间上更符合地理学第一定律,且在局部区域其迭代多次,插值稳定性较好,更适合于新待插点值的估计[19]。 对K层-Voronoi生成的1,…,K层自然邻近节点逐层迭代,并进行反距离加权获得φi(x)。由于K层-Voronoi的生成具有样点分布自适应性、规则唯一性和局部保形性,因此基于K-Voronoi插值同样具备上述特点,从而为构造几何结构约束的空间插值提供了基础。
2.3 结构自适应的插值算法
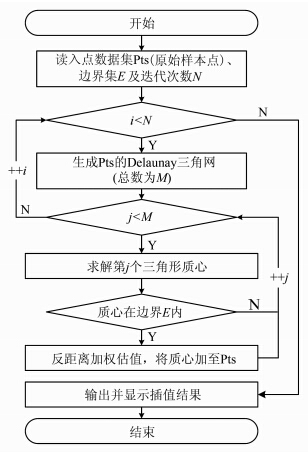
基于K层-Voronoi剖分构建基于V-邻域迭代的结构保持空间插值算法(见图 2)。首先对原始样本点进行第一次Delaunay剖分,以落入边界的三角形质心为待插点,对应的三角形顶点为控制点进行反距离加权插值。将估值后的质心追加至原样本点,然后对追加后的新样本点进行第二次Delaunay剖分,同样对边界内的三角形质心进行估值,再将新的待插点追加到该次插值样本点中继续下层空间剖分,超出迭代次数约束后算法终止,输出并显示插值结果。
|
| 图 2 算法流程 Fig. 2 Flow Chart of Algorithm |
日平均气温的空间插值要求在站网分布约束下较好地再现气温分布的空间结构[6, 7, 20],为此选用WMO(World Meteorological Organization)提供的中国主要城市气象站2013年6月1日平均气温数据进行算法评估。该数据在中国大陆共377个站位,空间分布不均,东部数据明显较西部数据分布密集,尤其是青藏高原地区气象站点甚少。通过 计算原始数据及各层插值结果的基本统计量、空间方差和空间协方差,以验证算法的结构保持特性和稳定性,进而将其与样条函数法(Spline)、自然邻点法(natural neighbor interpolation,NNI)、克里金法(Kriging)和反距离权重法(inverse distance weighted interpolation,IDW)进行对比,分析不同方法插值结果的统计参数特征。 3.2 算法自身空间保型性和稳定性验证
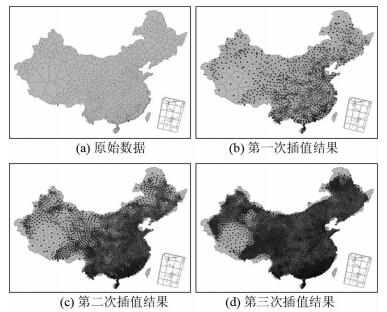
基于原始测站数据进行多层V-邻域结构自适应插值,各次迭代的结果见图 3。三次迭代后,插值点已具有较高的空间分布密度,各层插值结果均保持了原始数据东密西疏的分布特征结构,较好地再现了气温变化的整体构型。受中国复杂地形条件的影响,温度总体上呈阶梯性变化。原始数据和不同迭代次数插值数据的常规统计量和空间统计量分别见表 1和图 4。
|
| 图 3 不同迭代次数的自适应插值结果 Fig. 3 Adaptive Interpolation Results in Different Iterations |
| 原始点 | 一层插值 | 二层插值 | 三层插值 | Spline | NNI | Kriging | IDW | |
| 最小值 | 4.39 | 4.39 | 4.39 | 4.39 | -1.34 | 4.44 | 3.76 | 4.4 |
| 最大值 | 32.78 | 32.78 | 32.78 | 32.78 | 38.82 | 32.66 | 31.99 | 32.77 |
| 中位数 | 21.33 | 21.33 | 21.29 | 21.28 | 19.66 | 19.78 | 19.75 | 20.05 |
| 平均值 | 20.58 | 20.54 | 20.51 | 20.49 | 18.83 | 18.87 | 18.79 | 18.85 |
| 标准差 | 5.96 | 5.66 | 5.54 | 5.5 | 7.06 | 5.86 | 6.16 | 5.82 |
| 变异系数 | 0.29 | 0.28 | 0.27 | 0.27 | 0.37 | 0.31 | 0.33 | 0.31 |
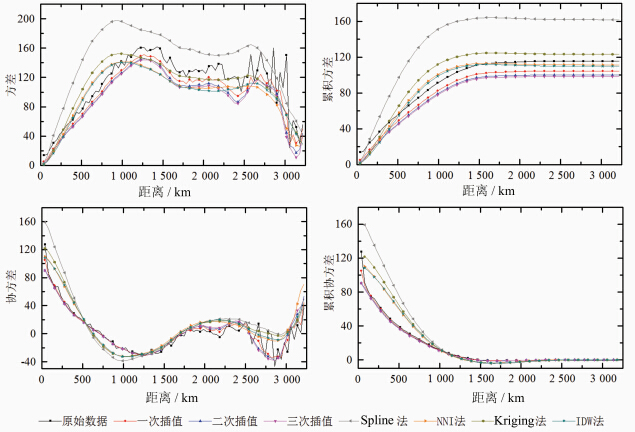
|
| 图 4 不同插值方法的空间统计量对比 Fig. 4 Comparison of Spatial Statistical Index with Different Interpolation Methods |
不同迭代次数的插值结果的最小值和最大值与原始数据一致,而均值和标准差随着插值层数的增加略有下降,这与迭代插值后数据分布的趋中性有关。变异系数上,各单次迭代插值具有一致的变异系数,且与原始数据的变异系数相差小于0.02。三次迭代无论在方差结构还是协方差结构上,均接近于原始数据,可很好地保持原有数据的空间分布特征。插值数据随着迭代次数的增加趋于平滑,导致其方差和协方差略有降低。总体上,本文方法的插值结果与原始数据的空间统计量对应性好,保持了原始数据的统计特征。
3.3 不同算法间的对比验证将3次迭代插值与Spline、NNI、Kriging和IDW方法进行算法对比(见表 1)。为方便对比,将所有方法的插值结果统一至10 m分辨率的格网,由于本文算法的插值结果具有不均匀性,采用不同格网内部所有插值点的均值作为格点值(见图 5)。
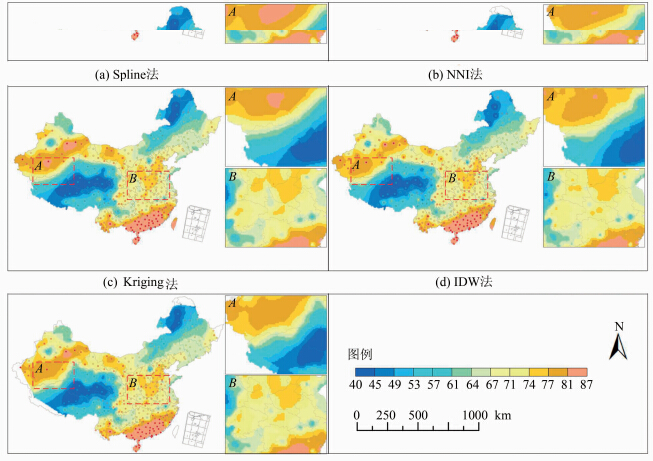
|
| 图 5 不同方法空间型的对比 Fig. 5 Comparison of Spatial Mode with Different Methods |
从图 5可以看出,Spline、Kriging和IDW方法在样点稀疏分布区域存在明显的条带分层,结构过渡连续性差。NNI和本文方法均是利用V-邻域结构的插值方法,在结构上也具有更高的相似性,但NNI仅利用V-邻域结构的顶点作为控制点进行一次插值,不能支持根据分布特征及插值分辨率需求的自适应控制点生成[13]。
本文算法通过限定待估点的影响范围,使权重分配符合原始数据的空间结构特征,稀疏区域的结构更精细,高、低值区域过渡更连续。统计指标对比也显示本文方法可很好地保持原始数据的空间分布信息,而其他方法的统计参量变化总体上更为显著。三次随机5%原始样点的交叉验证也显示本文算法具有较好的精度,可在样本数据结构特征保持和插值精度间取得较好平衡。 4 结 语
现有的插值方法多在理想数学假设的基础上构建,对样点数据空间分布结构的约束考虑不足,难以兼顾全局与局部精细结构的高精度再现,并很难保证对原始数据空间统计量的保持。本文基于K层-Voronoi结构建立了新的控制点生成方法,并利用Voronoi的局部保形特性和反距离加权实现了基于V-邻域结构约束的空间插值方法。本文算法的特性如下:①可以反映样本点分布结构与密度的层次自然近邻;②通过迭代插值获得不同分辨率插值数据的精细结构;③具有较好的稳定性、结构保形性和空间约束集成特性。
由于本文方法最终插值的分辨率与采样点分布相关,不同样点的分布可能导致插值结果的点位分布存在一定差异。该插值方法的层次在理论上可无限外推,因此可以根据样点分布特征及插值应用需求确定合适的插值层数;V-邻域结构作为常用的几何结构,具有高维的可拓展性,进而可支撑三维及高维数据插值;其在数据结构上的通用性和易集成性也利于V-邻域结构约束的空间插值方法与空间统计模型集成。
| [1] | Liu Yan, Ruan Huihua, Zhang Pu, et al. Kriging Interpolation of Snow Depth at the North of Tianshan Mountains Assisted by MODIS Data[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4):403-405(刘艳, 阮惠华, 张璞, 等.利用MODIS数据研究天山北麓Kriging雪深插值[J].武汉大学学报·信息科学版, 2012, 37(4):403-405) |
| [2] | Li Sha, Shu Hong, Xu Zhengquan. Interpolation of Temperature Based on Spatial-temporal Kriging[J]. Geomatics and Information Science of Wuhan University, 2012,37(2):237-241(李莎,舒红,徐正全.利用时空Kriging进行气温插值研究[J].武汉大学学报·信息科学版,2012,37(2):237-241) |
| [3] | Wang Yu, Zhu Changqing, Shi Wenzhong. Application of B Spline and Smoothing Spline on Interpolating the DEM Based on Rectangular Grid[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(3):240-244(王昱, 朱长青, 史文中. B 样条与磨光样条在基于矩形格网的 DEM 内插中的应用[J]. 测绘学报, 2000, 29(3):240-244) |
| [4] | Li J, Heap A D. A Review of Comparative Studies of Spatial Interpolation Methods in Environmental Sciences:Performance and Impact Factors[J]. Ecological Informatics, 2011, 6(3):228-241 |
| [5] | Guo D, Qu X, Huang L, et al. Sparsity-Based Spatial Interpolation in Wireless Sensor Networks[J]. Sensors, 2011, 11(3):2 385-2 407 |
| [6] | Hutchinson M F,McKenney D W, Lawrence K, et al. Development and Testing of Canada-Wide Interpolated Spatial Models of Daily Minimum-Maximum Temperature and Precipitation for 1961-2003[J]. Journal of Applied Meteorology and Climatology, 2009, 48(4):725-741 |
| [7] | ElKenawy A, López-Moreno J I, Stepanek P, et al. An Assessment of the Role of Homogenization Protocol in the Performance of Daily Temperature Series and Trends:Application to Northeastern Spain[J]. International Journal of Climatology, 2013, 33(1):87-108 |
| [8] | Zhu Huiyi, Liu Shulin, Jia Shaofeng. Problems of the Spatial Interpolation of Physical Geographical Elements[J]. Geographical Research, 2004, 23(4):425-432(朱会义, 刘述林, 贾绍凤. 自然地理要素空间插值的几个问题[J]. 地理研究, 2004, 23(4):425-432) |
| [9] | Shi Wenjiao, Yue Tianxiang, Shi Xiaoli, et al. Research Progress in Soil Property Inerpolators and Their Accuracy[J]. Journal of Natural Resources, 2012, 27(1):165-177 (史文娇, 岳天祥, 石晓丽, 等. 土壤连续属性空间插值方法及其精度的研究进展[J]. 自然资源学报, 2012, 27(1):165-177) |
| [10] | Zhao Xuesheng, Chen Jun, Wang Jinzhuang. QTM-based Algorithm for the Generating of Voronoi Diagram for Spherical Objects[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2):157-163(赵学胜,陈军,王金庄.基于QTM的球面Voronoi图的生成算法[J].测绘学报, 2002, 31(2):157-163) |
| [11] | Stahl K, Moore R D,Floyer J A, et al. Comparison of Approaches for Spatial Interpolation of Daily Air Temperature in a Large Region with Complex Topography and Highly Variable Station Density[J]. Agricultural and Forest Meteorology, 2006, 139(3):224-236 |
| [12] | Cromley R G, Hanink D M, Bentley G C. A Quantile Regression Approach to Areal Interpolation[J]. Annals of the Association of American Geographers, 2012, 102(4):763-777 |
| [13] | Okabe A, Boots B, Sugihara K, et al. Spatial Tessellations:Concepts and Applications of Voronoi Diagrams[M]. New York:John Wiley & Sons Ltd, 2009 |
| [14] | Chen J, Zhao R, Li Z.Voronoi-based K-Order Neighbor Relations for Spatial Analysis[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 59(1):60-72 |
| [15] | Ringler T, Ju L, Gunzburger M. A Multiresolution Method for Climate System Modeling:Application of Spherical Centroidal Voronoi Tessellations[J]. Ocean Dynamics, 2008, 58(5/6):475-498 |
| [16] | Yi Lin, Yuan Linwang, Luo Wen, et al. V-Neighbor Structure Based Spatial Interpolation Algorithm[J]. Geomatics and Information Science of Wuhan University, 2012, 37(11):1 285-1 288(易琳, 袁林旺, 罗文, 等. 顾及V-邻域结构的局部保形插值算法[J]. 武汉大学学报· 信息科学版, 2012, 37(11):1 285-1 288) |
| [17] | Xiong Minquan. Delaunay Triangulated Method with an Application to the Precipitation Interpolation[J]. Acta Meteorologica Sinica, 2012, 70(6):1 390-1 400(熊敏诠. Delaunay 三角剖分法在降水量插值中的应用[J]. 气象学报, 2012, 70(6):1 390-1 400) |
| [18] | Dong Jian,Peng Rencan,Zheng Yidong,et al.An Algorithm of Natural Neighbor Interpolation Based on Local Dynamic Optimal Voronoi Diagram and Its Application in Grid Digital Depth Model[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2):284-303(董箭, 彭认灿, 郑义东, 等. 局部动态最优 Voronoi 图的 NNI 算法及其在格网数字水深模型中的应用[J]. 测绘学报, 2013, 42(2):284-303) |
| [19] | Lu G Y, Wong D W. An Adaptive Inverse-Distance Weighting Spatial Interpolation Technique[J].Computers & Geosciences, 2008, 34(9):1 044-1 055 |
| [20] | Jarvis C H, Stuart N. A Comparison Among Strategies for Interpolating Maximum and Minimum Daily Air Temperatures. Part Ⅱ:The Interaction Between Number of Guiding Variables and the Type of Interpolation Method[J].Journal of Applied Meteorology, 2001, 40(6):1 075-1 084 |
 2015, Vol. 40
2015, Vol. 40



