文章信息
- 张国峰, 杨立荣
- ZHANG Guofeng, YANG Lirong
- 基于Copula的降水量不确定性建模
- Assessing the Local Uncertainty of Precipitation with Copulas
- 武汉大学学报·信息科学版, 2015, 40(6): 805-809
- Geomatics and Information Science of Wuhan University, 2015, 40(6): 805-809
- http://dx.doi.org/10.13203/j.whugis20130497
-
文章历史
- 收稿日期:2013-09-02
2. 海南省南海气象防灾减灾重点实验室, 海南 海口 570203;
3. 海南大学热带作物种质资源保护与开发利用教育部重点实验室, 海南 海口 570228
2. Key Laboratory of South China Sea Meteorological Disaster Prevention and Mitigation of Hainan Province, Haikou 570203, China;
3. Key Laboratory of Tropical Horticulture Resources and Genetic Improvement, Ministry of Education, Hainan University, Haikou 570228, China
气象观测站密度的相对稀疏使得降水量的插值一直是气象学、生态学、水文学等领域科学家研究的热点。通常各种插值算法对降水量的估计都存在误差,但确定性插值算法对未观测点只能给出一个估计值,不能对误差方差进行估计。以区域化变量理论为基础的克里格插值法不仅能给出无观测站位置的一个最优无偏估计,而且能给出估计的误差方差。克里格插值并不需要区域化变量满足多元正态假设,但如果利用克里格获取区域化变量在无观测站位置的概率密度函数,那么区域化变量必须满足多元正态假设。指示克里格可处理非正态分布或存在特异值的情形,但需要计算大量指示变异函数,且可能出现负概率、全概率大于1等现象。条件模拟具有相应插值方法的局限性,且需要通过大量模拟才能对局部不确定性给出估计。
就降水而言,现有的研究已证明一定区域短时段的降水量大多并不符合正态分布[1, 2, 3]。近年来发展起来的基于Copula的地统计学方法尤其适用于非正态数据的分析。Copula函数使得将多元分布函数分解为依赖结构和边缘分布分别进行研究成为可能。选择非正态边缘分布或非高斯Copula函数,就能对不同类型的非正态区域化变量进行建模。由于降水量分布通常有地域性特点(空间变异性很大),各种单一值插值方法常存在对极大降水估计过小、极小降水估计过大的问题,这对洪涝和干旱的评估是非常不利的。因此,对降水量进行不确定性插值,从不确定性的角度进行分析和决策不失为一种好的选择。本文尝试用基于Copula的地统计学方法对月降水量的不确定性进行建模,并将其与传统地统计学方法和经典统计学方法进行比较。
1 基于Copula的地统计学有关基于Copula的地统计学的详细论述可以参考文献[4, 5, 6, 7],这里只简述其主要内容。
1.1 参数估计设{Z(x)|x∈S}为一同质性随机场,x1,…,xn为互不相同的观测位置,S为研究区域。依据Skalar定理,Z(x1),…,Z(xn)之间的相关性可以用式(1)来刻画[8]:
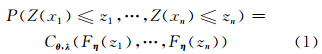
式中,Cθ,λ 代表n维Copula,参数向量θ和λ 控制它的相关性结构,不同的Copula对应不同的参数向量λ,参数向量θ控制着各向同性相关性函数模型,该相关性函数模型使上述Copula成为观测位置之间距离的函数;Fη为参数向量η决定的边缘分布函数,Fη不必处处相同。如果要引入空间趋势或者漂移变量,可以指定位置xi处分布函数的位置参数μi(xi)为:
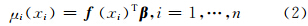
式中,f(xi)是以位置xi处的坐标构成的单项式为元素的漂移向量; β为回归系数向量。当Cθ,λ为高斯Copula,且Fη =Φμ,σ2 为高斯分布函数时,基于Copula的随机场模型就变为经典的高斯随机场模型。选择非高斯边缘分布或者非高斯Copula就可以建模非高斯区域化变量。当边缘分布函数为连续分布函数且使用高斯Copula时,可以如式(3)用极大似然函数法估计Θ=(θ ,λ ,η);而当使用χ2-Copula时,可以如式(4)用极大逐对似然函数法估计Θ=(θ ,λ ,η。
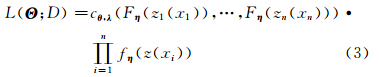
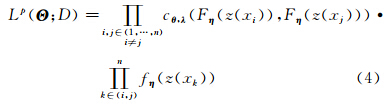
式中,c θ ,λ 代表Copula密度函数;f η 为边缘密度函数;D={z(x1),…,z(xn)}。
给定观测数据和Θ的估计值,对无观测站位置x0,其密度函数由式(5)给出。
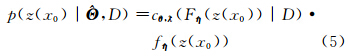
式中,cθ ,λ(·|D) 为条件Copula密度。预测分布的期望和方差可以分别通过式(6)和式(7)得到。
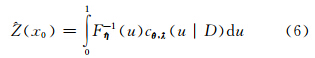
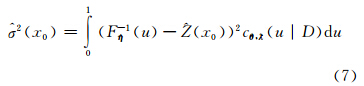
当区域化变量存在几何各向异性现象时,可以通过空间坐标的旋转和伸缩(式(8))将几何各向异性随机场变换成几何各向同性随机场。
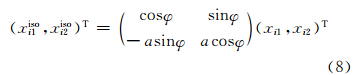
式中,a≥1为各向异性比率;φ∈[0,π]为各向异性角度。
spatialCopula[9]是一个可以完成基于Copula的空间分析的开源函数集。本文所有空间分析工作均由spatialCopula完成。
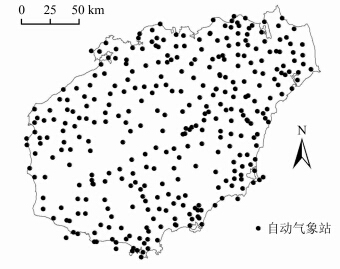
2 案例研究 2.1 资料与交叉验证选用2013年2月海南岛及其周围323个自动气象站观测的月雨量资料。323个自动气象站在海南岛及其周围的分布见图 1。图 2是323个自动气象站观测的月雨量的直方图。可见,上述月雨量资料存在严重右偏斜现象,也再次印证了已有的研究成果即一定区域的短时降水量通常为非正态分布。
|
| 图 1 自动气象站位置分布 Fig. 1 Automatic Weather Station Distribution |

|
| 图 2 2013年2月海南岛月降水量直方图 Fig. 2 AHistogram of Monthly Precipitation on Hainan Island in February,2013 |
对任意 p∈[0, 1],设αL=(1-p)/2,αU=(1+p)/2,FZ(xi)|z(-i),θ为某种地统计学方法通过交叉验证求得的第i个观测站的分布函数,则对于该方法,所有观测站的观测值落入概率为p的置信区间的份数由式(9)给出[10]:
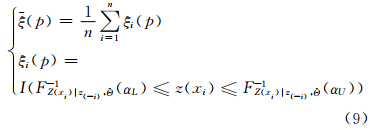
式中,I(·)为指示函数。理论上,对任意p∈[0, 1],应有ξ(p)=p。实际上,由于现实区域化变量的复杂性,只能通过 (p)与p的接近程度判断相应方法的优劣。
本文利用普通克里格 (ordinary Kriging,OK)、基于Box-Cox变换的OK和基于χ2-Copula的地统计学三种方法对上述月雨量的空间分布进行了分析。三种方法均考虑了几何各向异性,且都采用了式(10)所示的球型相关函数。
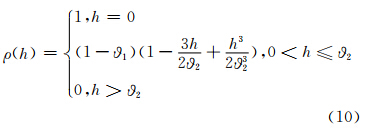
OK假定月雨量的概率分布为正态分布 (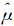 =19.4,
=19.4,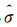 =29.35),估计的各向异性参数为â=1.19,
=29.35),估计的各向异性参数为â=1.19,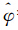 =1.98,相关函数参数为
=1.98,相关函数参数为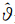 1=0.20,
1=0.20,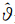 2=117.47;基于Box-Cox变换的OK估计的变换参数
2=117.47;基于Box-Cox变换的OK估计的变换参数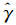 =0.36,变换后的正态分布参数为(
=0.36,变换后的正态分布参数为(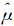 =1.6,
=1.6,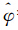 =4.44),各向异性参数为(1.34,1.53),相关函数参数为(0.20,268.83);而基于χ2-Copula的地统计学方法则采用了逆高斯分布(inverse Gaussian distribution,IG;
=4.44),各向异性参数为(1.34,1.53),相关函数参数为(0.20,268.83);而基于χ2-Copula的地统计学方法则采用了逆高斯分布(inverse Gaussian distribution,IG;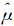 =21.15,
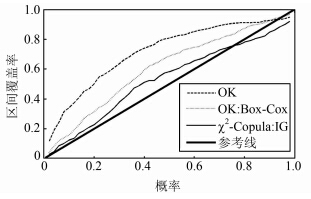
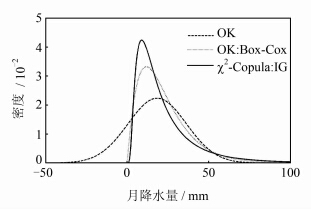
=21.15,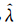 =1.70),估计的各向异性参数为(1.48,4.77),相关函数参数为(0.07,787.69)。依估计的模型参数和若干邻近观测站,先计算待估点和邻近观测站的Copula函数,然后依观测站的观测值计算条件Copula,最后根据式(5)计算待估点的概率密度函数,具体实现方法可进一步参考文献[4, 5, 6, 9]。图 3是三种方法交叉验证的结果。可见,对大多数的置信概率p,基于χ2-Copula的地统计学方法得到的置信区间的覆盖率比OK和基于Box-Cox变换的OK更接近理论值。图 4是三种方法对同一观测站(该站当月的降水量位于所有观测值的中值附近)交叉验证得到的概率密度函数。由于OK估计的概率密度函数在负值区依然有不为0的定义域,因此必然会出现降水量分位数为负值的情况。基于χ2-Copula的地统计学方法和基于Box-Cox变换的OK得到的概率密度函数在负值区不存在不为0的定义域,因而就从根本上避免了分位数为负值的现象。
=1.70),估计的各向异性参数为(1.48,4.77),相关函数参数为(0.07,787.69)。依估计的模型参数和若干邻近观测站,先计算待估点和邻近观测站的Copula函数,然后依观测站的观测值计算条件Copula,最后根据式(5)计算待估点的概率密度函数,具体实现方法可进一步参考文献[4, 5, 6, 9]。图 3是三种方法交叉验证的结果。可见,对大多数的置信概率p,基于χ2-Copula的地统计学方法得到的置信区间的覆盖率比OK和基于Box-Cox变换的OK更接近理论值。图 4是三种方法对同一观测站(该站当月的降水量位于所有观测值的中值附近)交叉验证得到的概率密度函数。由于OK估计的概率密度函数在负值区依然有不为0的定义域,因此必然会出现降水量分位数为负值的情况。基于χ2-Copula的地统计学方法和基于Box-Cox变换的OK得到的概率密度函数在负值区不存在不为0的定义域,因而就从根本上避免了分位数为负值的现象。
|
| 图 3 交叉验证置信区间的覆盖率 Fig. 3 Coverage of Cross-validation Confidence Intervals |
|
| 图 4 OK(虚线)、基于Box-Cox变换的OK(点线)和χ2-Copula(实线)对同一观测站交叉验证得到的概率密度函数 Fig. 4 Cross-validation Predictive Distributions Using OK,OK with Box-Cox Transformation and χ2-Copula for the Same Location |
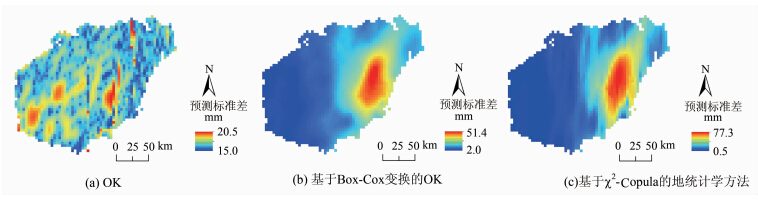
图 5是三种地统计学方法的预测标准差。可见,OK预测标准差仅与观测站的分布有关,与观测值无关;在观测站稀疏的区域,预测标准差相对较大,在观测站稠密的区域,预测标准差相对较小。基于χ2-Copula的地统计学方法和基于Box-Cox变换的OK得到的预测标准差具有相似的空间分布,且它们的预测标准差都与观测值的大小有关(在观测值小的区域,预测标准差较小,而在观测值大的区域,预测标准差较大)。但基于χ2-Copula的地统计学方法预测标准差的最小值比基于Box-Cox变换的OK预测标准差的最小值要小,而最大值比基于Box-Cox变换的OK预测标准差的最大值要大。
|
| 图 5 三种地统计学方法对2013年2月海南岛月降水量的预测标准差 Fig. 5 Predictive Standard Deviation for Monthly Precipitation on Hainan Island in February 2013 Using Different Geostatistical Models |
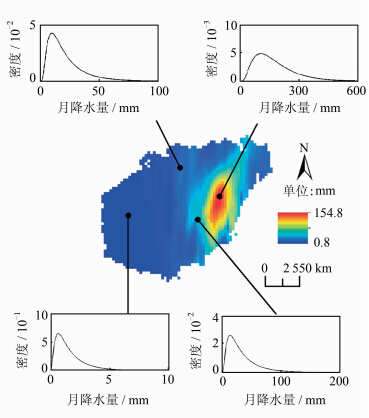
由图 6可见,基于χ2-Copula 的地统计学方法估计的4个无观测站位置的概率密度函数各不相同,且都呈右偏态。相比之下,经典的统计学方法是先制作区域月雨量的直方图,再根据直方图选择相应的概率密度函数类型进行拟合,然后用拟合的唯一的概率密度函数对区域内任一未观测位置进行概率描述。
|
| 图 6 基于χ2-Copula 的地统计学方法估计的2013年2月海南岛月降水量的期望分布图及4个无观测站位置的概率密度函数 Fig. 6 Expected Monthly Precipitation and Predicted PDFs for Four Arbitrary Locations on Hainan Island in February 2013 Using Geostatistical Models Based on χ2-Copula |
区域短时降水量的概率分布通常为非正态分布,如果强行利用OK(或带漂移的克里格等)对无观测站位置的降水量进行不确定性分析,那么得到的概率密度函数为正态密度函数,且可能会出现负分位数现象;基于Box-Cox变换的OK和基于Copula的地统计学方法则可以得到无观测站位置降水量的非正态概率密度函数,且不会出现负分位数现象。但交叉验证的结果表明,基于χ2-Copula的地统计学方法优于基于Box-Cox变换的OK。同经典统计学描述降水次网格空间不均匀性的方法相比,基于Copula的地统计学方法对研究区域内任意无观测站位置给出不同的概率密度函数。当降水量与海拔高度或者雷达、卫星资料的相关性较高时,基于Copula的地统计学方法可以漂移变量的形式融合这些资料。
| [1] | Zhang Xuewen, Ma Li. Entropy Meteorology[M]. Beijing:China Meteorological Press, 1992 (张学文, 马力. 熵气象学[M]. 北京:气象出版社, 1992) |
| [2] | Ding Yuguo. Research of Universality for Γ Distribution Model of Precipitation[J]. Chinese Journal of Atmospheric Sciences, 1994,18(5):552-560 (丁裕国. 降水量Γ分布模式的普适性研究[J]. 大气科学, 1994,18(5):552-560) |
| [3] | Cheng Bingyan, Gu Wanlong, Li Yun, et al. Function Relationship Between Daily Rainfall in China and Its Area in Horizontal Region[J]. Plateau Meteorology, 2005, 24(3):422-427 (程炳岩, 顾万龙, 李云, 等. 中国日降水量与其占有面积的函数关系[J]. 高原气象, 2005,24(3):422-427) |
| [4] | Bárdossy A. Copula-based Geostatistical Models for Groundwater Quality Parameters[J]. Water Resources Research, 2006, 42(11):W11416,DOI:10.1029/2005WR004754 |
| [5] | Bárdossy A, Li J. Geostatistical Interpolation Using Copulas[J]. Water Resources Research, 2008, 44(7):W07412, DOI:10.1029/2007WR006115 |
| [6] | Kazianka H, Pilz J. Copula-based Geostatistical Modeling of Continuous and Discrete Data Including Covariates[J]. Stochastic Environmental Research and Risk Assessment, 2010, 24(5):661-673 |
| [7] | Kazianka H, Pilz J. Bayesian Spatial Modeling and Interpolation Using Copulas[J]. Computers & Geosciences, 2011, 37(3):310-319 |
| [8] | Sklar A. Functions de Repartition a n Dimensions et Leurs Marges[J]. Publ Inst Stat Univ Paris, 1959, 8:229-231 |
| [9] | Kazianka H. spatialCopula:A Matlab Toolbox for Copula-based Spatial Analysis[J]. Stochastic Environmental Research and Risk Assessment, 2013, 27(1):121-135 |
| [10] | Goovaerts P. Geostatistical Modelling of Uncertainty in Soil Science[J]. Geoderma, 2001, 103(1/2):3-26 |
 2015, Vol. 40
2015, Vol. 40


