文章信息
- 李彬, 吴云, 李征航
- LI Bin, WU Yun, LI Zhenghang
- GNSS接收机自主完备性监测高级算法的有效性验证
- Validation of the GNSS Advanced ARAIM Algorithm
- 武汉大学学报·信息科学版, 2015, 40(6): 800-804
- Geomatics and Information Science of Wuhan University, 2015, 40(6): 800-804
- http://dx.doi.org/10.13203/j.whugis20130531
-
文章历史
- 收稿日期:2013-09-26
一直以来,GNSS接收机自主完备性监测(receiver autonomous integrity monitoring,RAIM)仅作为民航飞机在远洋/本土、终端区的辅助完备性监测手段。当飞机接近机场,进入垂直引导进近阶段时(完备性要求更高),主要依靠星基增强系统和地基增强系统的完备性监测来保证GNSS导航的安全性,而在没有外部增强系统的机场,飞机着陆则完全依靠飞行员的目视。随着GNSS的发展和完善,GNSS为民航提供垂直引导进近成为可能[1]。GNSS接收机自主完备性监测的高级算法ARAIM(advanced RAIM)正是为GNSS用于完备性和安全性更高的领域而提出的,如LPV-200(localizer performance with vertical guidance-200 feet)。ARAIM算法是传统RAIM算法的改进和扩展,更加严密和灵活。目前,ARAIM算法还在讨论中,GNSS在已形成的ARAIM算法下的性能表现和能否满足LPV-200阶段导航性能的要求[1, 2, 3],还需GNSS实测数据的验证。
1 ARAIM算法 1.1 测距误差模型
传统GNSS RAIM算法采用单频伪距观测值,在GNSS无故障状态下,假设测距误差服从零均值的高斯分布N(0,σRAIM2)。ARAIM算法则利用GNSS L1、L5载波相位平滑伪距观测值,假设测距误差服从期望值非零的高斯分布N(b,σARAIM2),其中,b吸收了GNSS无故障状态下卫星天线相位中心误差和信号传播过程中的形变,避免了σARAIM的膨胀。基于高斯分布N(b,σARAIM2),ARAIM算法在计算精度和完备性时采用两种不同的误差模型[1, 4, 5]。
1)计算精度的误差模型参数。 此时,高斯分布 N(b,σARAIM2)为:

式中,URE(user range error)为用户测距误差,反映卫星钟差和星历误差对测距影响的程度;bnom为GNSS无故障 状态下观测值的名义误差(nominal error);σacc_airborne为信号传播路径和接收机噪声引起的误差[5]。
2) 计算完备性的误差模型。 此时,高斯分布 N(b,σARAIM2)为:
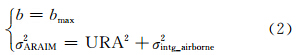
式中,URA(user range accuracy)为用户测距精度,指无故障状态下用来约束卫星钟差和星历误差所引起的URE的最小标准差,属于无偏高斯分布;bmax为GNSS无故障状态下观测值的最大偏差;σintg_airborne为信号传播路径和接收机噪声引起的误差[5]。
以上用于计算完备性的参数均要比用于计算精度的参数更为保守一些,如通常取URA为URE的两倍,以保障ARAIM对GNSS的安全保护。
1.2 基于多个假设检验的解分离方法 1.2.1 垂直保护水平
ARAIM算法采用多个假设理论来量化GNSS的导航风险,通过解分离方法对各个假设进行检验[6]。假设如下:根据GNSS导航时潜在风险的表现形式,将卫星工作状态分为三种情况:无卫星故障 H0、单颗卫星故障H1、H2、…、HN(N为卫星数)、多颗卫星同时故障(甚至星座故障)HM。
假设PHi(i=0,1,2,…,N,M)为各状态发生的概率,且彼此之间相互独立,则总的完备性风险PHMI (probability of hazardously misleading information)为[7]:
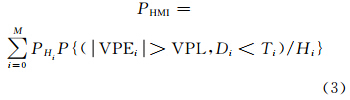
式中,P{( VPEi >VPL,Di<Ti)/Hi}为Hi假设下,将Hi中的错误卫星i剔除后垂直定位误差(vertical position error, VPE)大于垂直保护水平(vertical protection level, VPL)的概率;Di与Ti分别为Hi假设下,将Hi中错误卫星i剔除后的检验统计量与检验统计门限,与连续性风险有关,若Di>Ti,则GNSS的连续性中断。
若由式(3)计算得到的PHMI小于规定的完备性风险PHMI_Req,则GNSS满足完备性风险要求,可用于导航。在故障状态的假设下,当单颗卫星的故障率足够小时,如10-5/approach/sat(表示在每次进近过程中,单颗卫星出错的概率为10-5),则两颗及两颗以上卫星同时发生故障的概率远小于PHMI_Req。于是,可将两颗及两颗以上的卫星同时发生故障导致的完备性风险从式 (3) 中去除。设去除的完备性风险为PHMI_Un,有:
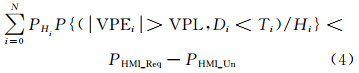
式中,N为ARAIM算法下需要计算的故障状态个数。反过来,如果将完备性风险PHMI_Req-PHMI_Un平均分配到各故障状态Hi下,可得到当前用户的 VPL。若VPE<VPL<VAL(vertical alert limit),即表示在规定的完备性风险下,GNSS可用,其中,VAL是规定的垂直定位误差告警限值。水平保护水平(horizontal protection level, HPL)的计算同上[2]。。
相对于传统RAIM算法只假设一颗卫星发生故障,该算法能兼顾GNSS导航时所有可能出错的状态,并一一量化,在算法上更严密、灵活。此外,为增强可用性,可通过动态优化分配完备性风险来降低VPL值。 1.2.2 精度
LPV-200阶段要求GNSS无故障状态下95%置信水平下的VPE小于4 m,即

1.2.3 有效监测阈值EMT
EMT(effective monitor threshold)是导航系统故障状态下对VPE的约束,要求GNSS发生故障时在ARAIM保护下的VPE超过15 m的概率不大于1×10-5;当概率取1×10-5时,可确定该状态下VPE的限值EMT。
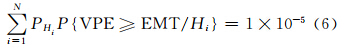
1.2.4 连续性风险
在ARAIM算法中,根据多假设理论对各假设状态下的检验统计量进行假设检验,若T>D,即认为GNSS故障。LPV-200阶段要求垂直方向的连续性风险(即误警率)为4×10-6/15 s,即

2 ARAIM算法的有效性验证
本文以bake站为例,首先计算得到bake站等9个IGS站(分布于南北半球)连续10 d的GNSS(GPS、GPS/GLONASS两种模式)VPE,并将VPE与ARAIM预测的VPL、P精度和EMT进行比较,分析ARAIM算法的有效性。对这9个IGS站的观测值进行解分离的故障检测,统计各站点的实际连续性风险。最后根据LPV-200对以上指标性能的要求,评定两种模式下各IGS站的可用性。
由于垂直方向的完备性要求高于水平方向[1],且GNSS在垂直方向上的卫星几何强度要弱于水平方向,所以本文主要分析ARAIM算法在垂直方向上的性能表现。
2.1 ARAIM相关参数的设置
本文根据相关文献对涉及的必要参数设置如下[1, 2, 8]: 完备性风险为8.7×10-8/approach,误警率为4×10-6/15 s,单颗卫星的出错率为10-5/approach/sat,名义误差为0.1 m,最大偏差为0.5 m;GPS URA为1.0 m,URE为0.5 m;GLONASS URA为2.0 m,URE为1.0 m[9]。
2.2 实测数据对ARAIM算法的有效性验证 2.2.1 垂直保护水平
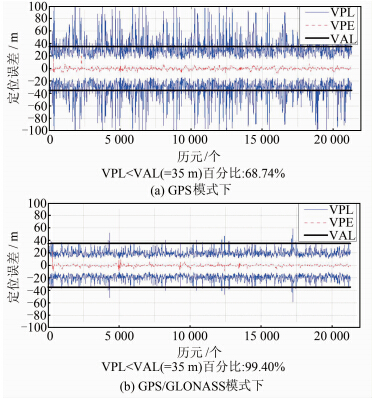
图 1分别为两种模式下bake站10 d内的VPE、VPL与VAL。
|
| 图 1 GPS和GPS/GLONASS模式下的VPE、VPL、VAL Fig. 1 VPE,VPL and VAL Under GPS and GPS/GLONASS Modes |
对图 1统计得出,两种模式下ARAIM预测得到的VPL均大于由实测数据计算得到的VPE,说明在给定的完备性风险和连续性风险下,ARAIM没有发生危险误导信息。将VPL与VAL比较,GPS导航时,VPL小于VAL的百分比为68.74%;GPS/GLONASS导航时,这一比例达99.40%,说明双系统联合导航时,卫星几何增强在很大程度上降低了VPL值,并抑制其大幅波动,增强了系统可用性。 2.2.2 精度
图 2分别为两种模式下由实测数据计算得到的VPE和ARAIM预测得到的P精度。图 2中虚曲线为实测数据得到的VPE;实曲线为根据ARAIM算法预测得到的P精度,黑直线为4 m的精度限值。

|
| 图 2 GPS和GPS/GLONASS模式下的精度 Fig. 2 Accuracy Under GPS and GPS/GLONASS Modes |
对图 2统计得出,GPS、GPS/GLONASS无故障状态下的VPE小于P精度的比例分别为95.02%和95.50%,这与§1.2.2关于P精度的定义吻合,说明在GNSS无故障状态下,P精度能够对95%置信度下VPE的精度进行很好的预测。P精度和4 m限值相比较,GPS/GLONASS模式下的P精度小于4 m限值的比例为100%,优于GPS模式下的P精度小于4 m限值的比例为98.22%,完全满足LPV-200的导航性能要求。 2.2.3 有效监测阈值
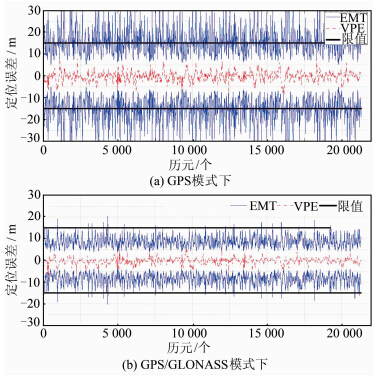
图 3分别为两种模式下由实测数据得到的VPE和ARAIM预测得到的EMT。图 3中虚 曲线为通过实测数据得到的VPE;实曲线为根据对图 3统计得出,GPS、GPS/GLONASS状态下,VPE小于EMT的比例分别为99.99%和100%,在单颗卫星故障率为 10-5/approach/sat的条件下,与§1.2.3关于EMT的解释吻合,表明GNSS故障状态下,EMT能够对VPE进行很好的约束;EMT和15 m限值相比较,GPS/GLONASS模式下,EMT小于15 m限值的比例为99.91%,远远优于GPS模式下EMT小于15 m限值的比例46.25%,完全满足LPV-200的导航性能要求。
|
| 图 3 GPS和GPS/GLONASS模式下的EMT Fig. 3 EMT Under GPS and GPS/GLONASS Modes |
ARAIM算法预测得到的EMT,黑直线为15 m的EMT限值。 2.2.4 ARAIM算法的有效性分析
表 1是在两种模式下对bake站等9个IGS站通过ARAIM算法预测得到的VPL、P精度、EMT的有效性统计。
| IGS站 | GPS | GPS/GLONASS | ||||
| VPE<VPL | VPE<P精度 | VPE<EMT | VPE<VPL | VPE<P精度 | VPE<EMT | |
| bake | 100 | 95.02 | 99.99 | 100 | 95.50 | 100 |
| hofn | 100 | 90.06 | 96.45 | 100 | 94.05 | 99.92 |
| gold | 100 | 90.22 | 100 | 100 | 92.89 | 100 |
| mdvj | 100 | 95.58 | 100 | 100 | 94.67 | 100 |
| kouc | 100 | 92.76 | 98.78 | 100 | 96.11 | 100 |
| maw1 | 100 | 95.31 | 99.87 | 100 | 94.42 | 99.96 |
| rcmn | 100 | 95.06 | 100 | 100 | 95.60 | 100 |
| sthl | 100 | 93.31 | 97.43 | 100 | 93.67 | 99.98 |
| xmis | 100 | 94.01 | 98.58 | 100 | 95.23 | 100 |
| 最大值 | 100 | 95.58 | 100 | 100 | 96.11 | 100 |
| 最小值 | 100 | 90.06 | 96.45 | 100 | 92.89 | 99.92 |
| 平均值 | 100 | 93.48 | 99.01 | 100 | 94.68 | 99.98 |
对各站点 GPS、GPS/GLONASS模式下的VPL、P精度、EMT的有效性进行统计,结果如下:①两种模式下预测得到的VPL均大于由实测数据计算得到的VPE,即GPS、GPS/GLONASS模式下VPL的有效性均为100%;②GPS模式下P精度大于VPE的比例最大为95.58%,最小为90.06%,平均为93.48%,即GPS模式下P精度的有效性为93.48%;GPS/GLONASS模式下P精度 的有效性为94.68%;③GPS模式下,EMT大于VPE的比例最大为100%,最小为96.45%,平均为99.01%,即GPS 模式下EMT的有效性为99.01%,GPS/GLONASS模式下EMT的有效性为99.98%。结果表明,由ARAIM算法预测得到的VPL、P精度、EMT均能有效涵盖由GNSS实测 数 据计算得到的VPE的范围,验证了ARAIM 算法在预测VPL、P精度、EMT方面的有效性。
2.3 GNSS的可用性
由实测数据得到垂直方向上的检验统计量 T和该假设状态下检验统计门限D,统计出T>D的个数,并将其转化为以15 s为单位的连续性风险。当GPS独立导航时,连续性风险为0.3×10-7/15 s;当GPS/GLONASS导航时,连续性风险为7×10-7/15 s。两种模式下的连续性风险均满足LPV-200的导航性能要求。其余站的连续性风险结果亦满足要求。
基于以上数据结果,根据 GNSS的可用性要求[1, 10],即当同时满足VPL<35 m,P精度<4 m,EMT<15 m,连续性风险小于4×10-6/15 s时,来评估ARAIM算法下各站点的GNSS可用性水平,结果见表 2。
| bake | hofn | gold | mdvj | kouc | mawl | rcmn | sthl | xmis | |
| GPS | 44.78 | 59.18 | 63.01 | 49.25 | 67.69 | 59.01 | 75.62 | 50.62 | 71.02 |
| GPS/GLONASS | 99.22 | 99.42 | 99.11 | 99.25 | 98.87 | 99.58 | 99.34 | 99.00 | 99.10 |
从表 2看出,在满足VPL、P精度、EMT和连续性风险条件下,GPS模式下各站点的可用性均不高,最高为75.62%; GPS/GLONASS模式下的可用性基本都达到99%以上,相对于GPS模式,可用性水平提高了65%以上。结果表明,在当前单系统导航的情况下,仅依靠ARAIM还无法在其覆盖范围内为民航提供LPV-200服务的能力,而两个系统间的联合导航则会大大提高ARAIM算法下的GNSS可用性水平,其性能表现能够满足LPV-200阶段的导航性能要求。未来随着GPS、BeiDou、GLONASS及Galileo任意三个及三个以上系统间的联合导航[11],卫星几何强度会大大增强,在ARAIM监测下,GNSS可用性水平将会进一步提高。
3 结 语
本文重点研究了基于多个假设检验理论的ARAIM算法,利用分布在不同地理位置的9个IGS站的实测数据对ARAIM算法进行了验证。基于LPV-200的导航性能要求,分别对GPS和GPS/GLONASS下各IGS站的可用性水平进行了评估,得出如下结论。
1)通过GNSS实测数据得到的VPE与ARAIM算法预测的VPL、P精度、EMT及连续性风险的预测结果基本一致,验证了ARAIM算法在估计VPL、P精度、EMT及连续性风险方面的有效性。
2)在ARAIM监测下,GPS独立导航时为LPV-200提供的可用性不高,最高为75.62%,GPS/GLONASS联合导航时为LPV-200提供的可用性基本都达到99%以上,满足LPV-200阶段的导航性能要求。
实际上,在LPV-200阶段,接收机处在高速航行的动态环境中,接收机接收的卫星信号可能会出现失锁等现象,其动态数据质量要比基准站的静态数据质量差。因此,本文结论会比飞机在高速航行的动态环境下得到的结果相对乐观。
| [1] |
FAA-GEAS-Panel. Phase Ⅱ of the GNSS Evolutionary Architecture Study[EB/OL].http://www.faa.gov/about/office_org/headquarters_offices/ato/service_units/techops/navservices/gnss/library/documents/med ia/GEASPhaseⅡ_Final.pdf,2010 |
| [2] | Blanch J, Walter T, Enge P. Advanced RAIM User Algorithm Description:Integrity Support Message Processing, Fault Detection, Exclusion, and Protection Level Calculation[C]. The 25th International Technical Meeting of the Satellite Division of the Institute of Navigation,Nashville, TN, 2007 |
| [3] | Wu Yun, Wang Jinling, Jiang Yiping. Advanced Receiver Autonomous Integrity Monitoring (ARAIM) Schemes with GNSS Time Offsets[J]. Advances in Space Research, 2013, 52(1):52-61 |
| [4] | Choi M, Blanch J, Akos D, et al. Demonstrations of Multi-Constellation Advanced RAIM for Vertical Guidance Using GPS and GLONASS Signals[C]. The 24th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, 2011 |
| [5] | Lee Y C, McLaughlin M P. Feasibility Analysis of RAIM to Provide LPV-200 Approaches with Future GPS[C]. ION GNSS 20th International Technical Meeting of the Satellite Division, Fort Worth, TX, 2007 |
| [6] | Pervan B S, Pullen S P, Christie J R. A Multiple Hypothesis Approach to Satellite Navigation Integrity[J]. Journal of the Institute of Navigation, 1998, 45(1):61-71 |
| [7] | Blanch J, Walter T, Enge P, et al. Integrity Support Message Processing, Fault Detection, Exclusion, and Protection Level Calculation[C]. The 25th International Technical Meeting of the Satellite Division of the Institute of Navigation,Nashville, TN,2012 |
| [8] | WAAS MOPS. Minimum Operational Performance Standards for Global Positioning System/Wide Area Augmentation System Airborne Equipment[R]. RTCA/DO-229C, Washington D C,2001 |
| [9] | Heng L, Gao G X, Walter T, et al. Statistical Characterization of GLONASS Broadcast Ephemeris Errors[C]. The 24th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, 2011 |
| [10] | Walter T, Enge P, Blanch J, et al. Worldwide Vertical Guidance of Aircraft Based on Modernized GPS and New Integrity Augmentations[J]. IEEE, 2008, 96(12):1 918-1 935 |
| [11] | Wu Yun, Yang Xinchun, Chen Hui, et al. Simulation and Analysis of EGNOS System's Integrity Under Multi-system with Multi-frequency[J]. Geomatics and Information Science of Wuhan University, 2012, 37(3):269-273 (吴云,杨鑫春,陈慧, 等.多频多系统的ENGOS系统完备性模拟分析[J]. 武汉大学学报·信息科学版,2012,37(3):269-273) |
 2015, Vol. 40
2015, Vol. 40



