文章信息
- 范丽红, 王利, 张明, 郑增记
- FAN Lihong, WANG Li, ZHANG Ming, ZHENG Zengji
- 基于MW与STPIR组合的周跳探测与修复方法研究
- A Combination of MW and Second-order Time-difference Phase Ionospheric Residual for Cycle Slip Detection and Repair
- 武汉大学学报·信息科学版, 2015, 40(6): 790-794
- Geomatics and Information Science of Wuhan University, 2015, 40(6): 790-794
- http://dx.doi.org/10.13203/j.whugis20130521
-
文章历史
- 收稿日期:2013-09-23
2. 西部矿产资源与地质工程教育部重点实验室, 陕西 西安 710054;
3. 陕西省地震局, 陕西 西安 710068
2. Key Laboratory of Western China's Mineral Resources and Geological Engineering, Ministry of Education, Xi'an 710054, China;
3. Shaanxi Seismological Bureau, Xi'an 710068, China
利用载波相位观测值在准确固定模糊度和探测与修复周跳的情况下可以得到更高精度的导航和定位结果,因此,准确地探测和修复周跳对高精度导航定位是非常必要的。目前常用的周跳处理方法有高次差法[1]、相位减伪距法[2]、多普勒观测值法[3]、TurboEdit[4, 5, 6, 7, 8, 9, 10]、小波分析法[11]等,但高次差法无法准确探测非独立周跳;相位减伪距法受到伪距观测值精度的影响,无法探测出小周跳;多普勒观测值受到观测数据采样间隔的影响,探测效果不佳;TurboEdit中的电离层残差组合受电离层误差的影响较大,且存在探测的不敏感性[5]。本文针对电离层残差法受电离层影响较大的问题,用相位电离层残差组合二次历元间差分(second-order time-difference phase ionospheric residual,STPIR)进行周跳探测,联合MW(Melbourne-Wbbena)组合进行周跳的探测与修复,并通过实例验证了该方法的可靠性和有效性。
1 周跳探测的基本理论
去除对流层、多路径及观测噪声后的相位和伪距观测方程为:
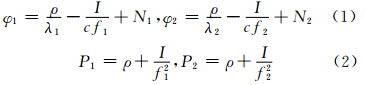
式中,φ表示载波相位观测值;P表示伪距观测值;λ表示载波波长;I表示电离层参数;ρ表示卫星至接收机的几何距离;c表示光速;N表示载波相位模糊度;f表示载波的频率。
1.1 MW组合
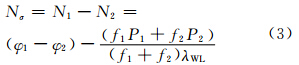
对于MW组合,对Nσ值从第1个历元至第i个历元的i个Nσ的均值
式中,
如果要探测第i+1个历元,先计算前面i个历元宽巷模糊度的平均值
就认为第i+1个历元的载波相位观测值中存在周跳;若不满足,则认为没有周跳。当出现周跳时,标记出该颗卫星出现周跳的历元,重新进行初始化,重复上述过程。但是当两个频率上出现等周跳即Nσ=0时,该方法无法探测出周跳[6, 7, 9]。
1.2 相位电离层残差组合二次历元间差分(STPIR)
相位电离层残差组合也可表示为:
其中,Ires=- I λ1f12 (1- f12 f22 )=1.369 8I为以周为单位的电离层残差项。
从式(7)可以看出,该组合包含频率间电离层影响之差、频率间模糊度之差、频率间多路径效应之差和接收机噪声。对式(7)进行历元间求差,则有:
式中,周跳检验量
在二阶历元间差分中,电离层残差明显小于一阶历元间差分值,始终在0附近波动,从而有利于周跳探测[5]。
假设L1和L2的测量中误差均为mφ=±0.01周,根据式(9),由误差传播率知:
则有mD2=0.032 5周。以4倍检测量中误差为限差,可知限差为±0.13周。也就是当两个载波上的周跳引起的历元间电离层残差检验量D2变化值大于0.13周时,就能探测出周跳。但该组合无法探测出
1.3 联合探测与修复周跳
由于 MW组合与STPIR组合均存在探测的不敏感性,且两种方法只能探测出周跳的位置却不能分离出周跳,因此将两种方法探测的结果结合起来,对于探测到同一历元的周跳只取其一,而各自探测的不敏感部分可相互补充,从而能更彻底地探测周跳。
将MW组合与STPIR组合联合如下:
通过式(11)便可分离出L1、L2的周跳。
2 实例与分析
本文选取了实际观测的dt=5 s静态4 h观测数据中的G01卫星和机载dt=5 s动态2 h观测数据中的G09卫星,并人工加入周跳,利用上述方法对加入周跳前后的数据进行处理分析。表 1是对加入的待检验周跳的说明。这里所说的在某一历元加入周跳,是指从该时刻起之后的所有历元均加入相应值。
图 1为dt=5 s的静态观测数据加入周跳前后的MW组合观测值及其历元间变化值的序列图。
图 2为dt=5 s的静态观测数据加入周跳前后的STPIR组合观测值及其变化值的序列图。
图 3为dt=5 s的动态观测数据加入周跳前后的MW组合观测值及其历元间变化值和中误差限差的序列图。图 4为dt=5 s的动态观测数据加入周跳前后的STPIR组合观测值及其变化值的序列图。
从图 1(a)和图 3(a)可以看出,对于没有加入周跳的观测数据,MW组合观测值在一常数附近波动。图 1(b)和图 3(b)则说明对于加入的(4,3)、(5,4)、(6,7)、(9,7)周的大周跳均有明显的变化;对于加入的(1,0)、(0,-1)周的小周跳也有明 显变化,但对于(1,1)周的相等周跳没有变化,无法探测。
从图 2和图 4可以看出,对于没有周跳的观测数据,STPIR检验量是很小的值,当数据中有周跳存在,检验量会有明显的变化,超过阈值。但对于(9,7)组合的周跳,周跳检验量的波形变化很小,无法探测出来。
表 2和表 3为联合MW组合与STPIR组合进行周跳探测与修复的结果。
可以看出,在dt=5 s的观测数据中,联合MW组合与STPIR组合相互补充了单个组合的不足,可以探测出所有组合的周跳。
在进行周跳探测时,相位电离层二阶差分组合消除了电离层高阶项的影响,更有利于进行周跳的探测。分别利用MW组合与STPIR组合探测周跳时均存在探测的不敏感性,将二者相结合可相互补充,能更彻底地探测与修复小周跳。下一步可以继续研究在该算法中区别周跳和粗差,并考虑将该算法应用到实时周跳的探测与修复中。
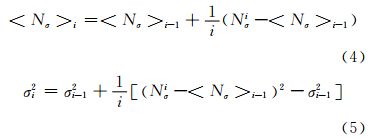
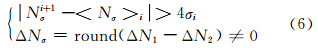
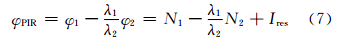
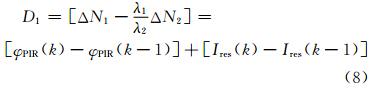
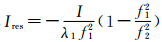 受电离层残差的影响可达到1.369 8 I(k)-I(k-1) ,且当采样间隔增大时,相邻历元间的电离层变化增大。为了减小电离层扰动的影响,对电离层残差组合进行二阶历元间差分[5]:
受电离层残差的影响可达到1.369 8 I(k)-I(k-1) ,且当采样间隔增大时,相邻历元间的电离层变化增大。为了减小电离层扰动的影响,对电离层残差组合进行二阶历元间差分[5]:
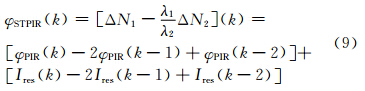
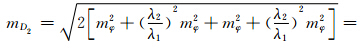
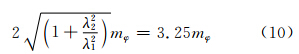
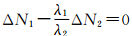 的周跳[6, 7]。
的周跳[6, 7]。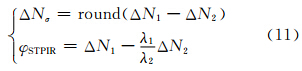
周跳 静态(dt=5 s) 动态(dt=5 s)
L1 L2 时间 历元 时间 历元
1 1 13:30 361 0:15 181
4 3 14:00 721 0:30 361
5 4 14:30 1 081 0:45 541
6 7 15:00 1 441 1:00 721
9 7 15:30 1 801 1:15 901
1 0 16:00 2 161 1:30 1 081
0 -1 16:30 2 521 1:45 1 261
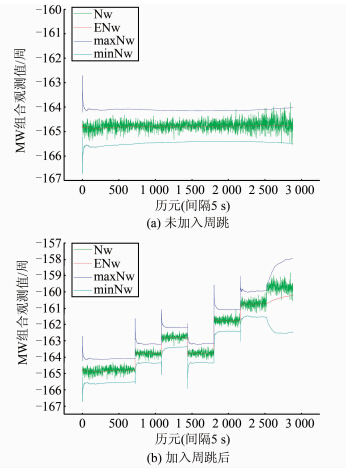
图 1 加入周跳前后G01卫星的MW组合序列
Fig. 1 Time Series of MW Combination for G01
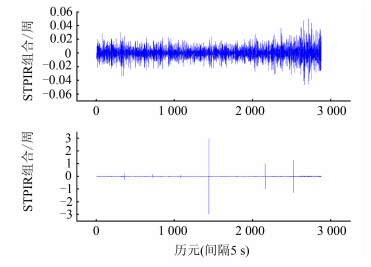
图 2 加入周跳前后G01卫星的STPIR组合序列
Fig. 2 Time Series of STPIR Combination for G01
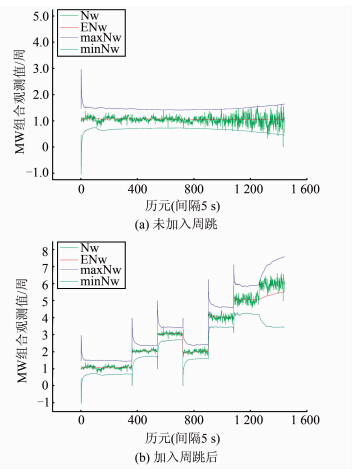
图 3 加入周跳前后G09卫星的MW组合序列
Fig. 3 Time Series of MW Combination for G09
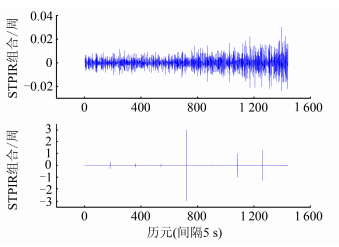
图 4 加入周跳前后G09卫星的STPIR组合序列
Fig. 4 Time Series of STPIR Combination for G09
历元
L1加入周跳
L2加入周跳
ΔNσ
φSTPIR
ΔN1
ΔN2
是否可探测周跳
361
1
1
0
-0.282 183
1
1
Yes
721
4
3
1
0.151 500
4
3
Yes
1 081
5
4
1
-0.132 716
5
4
Yes
1 441
6
7
-1
-2.976 033
6
7
Yes
1 801
9
7
2
0.035 050
9
7
Yes
2 161
1
0
1
0.999 983
1
0
Yes
2 521
0
-1
1
1.273 866
0
-1
Yes
历元
L1加入周跳 L2加入周跳
ΔNσ
φSTPIR
ΔN1
ΔN2
是否可探测周跳
181
1
1
0
-0.284 533
1
1
Yes
361
4
3
1
0.150 200
4
3
Yes
541
5
4
1
-0.131 966
5
4
Yes
721
6
7
-1
-2.989 766
6
7
Yes
901
9
7
2
0.015 400
9
7
Yes
1 081
1
0
1
0.994 783
1
0
Yes
1 261
0
-1
1
1.280 883
0
-1
Yes
| [1] | Wang Aisheng, Ou Jikun. Sequential Characteristics and Accurate Estimation of Cycle Slips in High Order Differential[J]. Journal of Geodesy and Geodynamics, 2008,28(5):59-64(王爱生, 欧吉坤. 周跳在高阶差分中的时序特征及精确估计[J]. 大地测量与地球动力学, 2008, 28(5):59-64) |
| [2] | Chen Pinxin, Zhang Chuanyin, Huang Kunxue. Cycle Slips Detecting and Repairing by Use of Phase Reduce Pseudorange Law and Ionized Layer Remnant Method of Difference[J]. Journal of Geodesy and Geodynamics, 2010, 20(2):120-124(陈品馨, 章传银, 黄昆学.用相位减伪距法和电离层残差法探测和修复周跳[J].大地测量与地球动力学, 2010, 20(2):120-124) |
| [3] | Chang Zhiqiao, Hao Jinming, Li Junyi. Cycle Slips and Gross Error Checkout Using Doppler Observations[J]. Bulletin of Surveying and Mapping, 2008(3):28-30(常志巧, 郝金明, 李俊义.利用多普勒观测检测周跳的粗差[J]. 测绘通报, 2008(3):28-30) |
| [4] | Blewitt G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990,17(3):199-202 |
| [5] | Cai Changsheng, Liu Zhizhao, Xia Pengfei,et al. Cycle Slip Detection and Repair for Undifferenced GPS Observations Under High Ionospheric Activity[J]. GPS Solution, 2012,17(2):247-260 |
| [6] | Fang Rongxin, Shi Chuang, Wei Na, et al. Real-time Cycle-slip Detection for Quality Control of GPS Measurements[J]. Geomatics and Information Science of Wuhan University, 2009, 34(9):1 094-1 097(方荣新, 施闯, 魏娜,等.GPS数据质量控制中实时周跳探测研究[J]. 武汉大学学报·信息科学版, 2009, 34(9):1 094-1 097) |
| [7] | Cai Hua, Zhao Qile, Sun Hanrong, et al. GNSS Real-time Data Quality Control[J]. Geomatics and Information Science of Wuhan University, 2011,36(7):820-824(蔡华, 赵齐乐, 孙汉荣,等. GNSS实时数据质量控制[J]. 武汉大学学报·信息科学版, 2011, 36(7):820-824) |
| [8] | Zhen Dai. Matlab Software for GPS Cycle-slip Processing[J]. GPS Solution, 2012, 16(2):267-272 |
| [9] | Wang Wei, Wang Jiexian, Gao Junqiang. Cycle Slip Detection of GPS Data[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6):687-690(王维, 王解先, 高俊强. GPS周跳探测的方法研究[J]. 武汉大学学报·信息科学版, 2010, 35(6):687-690) |
| [10] | Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan:Wuhan University Press, 2005(李征航, 黄劲松. GPS测量与数据处理[M]. 武汉:武汉大学出版社, 2005) |
| [11] | Huang Dingfa, Zhuo Jiancheng. Wavelet Analysis for Cycle Slip Detection and Reconstruction of GPS Carrier Phase Measurement[J]. Acta Geodaetica et Cartographica Sinica, 1997, 26(4):352-357(黄丁发, 卓健成. GPS相位观测值周跳检测的小波分析法[J]. 测绘学报, 1997, 26(4):352-357) |
 2015, Vol. 40
2015, Vol. 40



