文章信息
- 郭杰, 归庆明, 郭淑妹, 张宁
- GUO Jie, GUI Qingming, GUO Shumei, ZHANG Ning
- 利用复共线性诊断确定偏差矫正项的截断型岭估计
- Truncation Ridge Estimation Based on the Biased-corrected Theory by Multicollinearity Diagnosis
- 武汉大学学报·信息科学版, 2015, 40(6): 785-789
- Geomatics and Information Science of Wuhan University, 2015, 40(6): 785-789
- http://dx.doi.org/10.13203/j.whugis20130465
-
文章历史
- 收稿日期:2013-09-05
考虑线性模型:
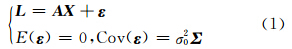
式中,L 为n×1观测向量; A 为n×t设计矩阵;rank( A )=r=t; X 为t×1未知参数向量; ε 为n×1的观测误差向量;σ02为未知的单位权方差; Σ 为正定权方差阵。故存在唯一的正定对称阵 ,用
,用 左乘式(1),并记
左乘式(1),并记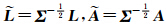 ,Δ =
,Δ = ε ,Δ 为n×1的各分量等精度不相关的观测误差向量,则得
ε ,Δ 为n×1的各分量等精度不相关的观测误差向量,则得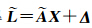 ,E( Δ )=0,Cov( Δ )=σ02 I n。
因此,不妨考虑如下线性模型:
,E( Δ )=0,Cov( Δ )=σ02 I n。
因此,不妨考虑如下线性模型:

则未知参数的最小二乘估计为:

当设计阵存在复共线性时,最小二乘估计虽是最优线性无偏估计,但其本身的方差很大,表现得极不稳定,此时有偏估计是改善最小二乘估计的有效方法。目前,文献中关于有偏估计的研究日趋完善,成果颇丰。最早由 Hoerl和Kennard[1]提出的岭估计是几十年来应用最广的一类有偏估计。随着实践的不断深入,各种组合估计应运而生,并得到成功运用[2, 3, 4]。目前,多数学者青睐于对岭估计和Liu估计的研究,大量文献对其性质和参数的确定方法进行了讨论,并提出各种推广、修正的估计[5, 6, 7]。在实际中,除了由模型本身所给出的样本信息之外,还可以获得对待估参数的某种附加信息,从而得到各种附加约束条件的估计[8, 9]。文献[10]基于矩阵的奇异值分解(singular value decomposition,SVD)理论,通过修改设计阵的奇异值,提出了病态方程的直接解算方法,同样达到了提高参数估值的准确性和稳定性的效果。
这些有偏估计都是针对法矩阵或者设计阵的病态性提出的有益探索,既然是有偏估计,必然存在偏差,且正则化估值的偏差计算公式在文献[1]中已经给出,文献[11, 12, 13]正是利用估值的偏差或残差的偏差对正则化方法进行的研究和分析,并提出了偏差矫正理论。文献[11]在模型参数无先验信息的前提下,首先考察未知参数的正则解对方差分量偏差的影响,接着利用偏差矫正后的残差来估计方差分量,从而提出偏差矫正的方差分量估计。文献[12]对广义交叉核检法(generalized cross validation,GCV)进行了推广,并利用该方法确定了模型的正则化参数和方差分量两组未知量,在估计方差分量时,用到了偏差矫正的方差分量估计法。受到应用偏差矫正进行方差分量估计法的启发,文献[13]利用偏差矫正的理论对未知参数进行了估计,具体来说,首先得到普通正则解,计算其偏差,然后从普通正则解中去掉偏差,得到完全偏差矫正的正则解和部分偏差矫正的正则解,并给出部分偏差矫正的正则解在均方误差意义下优于普通正则解的第一个分析性条件,注意到趋于零的小奇异值对应的偏差很大,因此偏差矫正时应避开小奇异值对应项,由此得第二个条件。仅对满足这两个条件的未知参数分量进行偏差矫正,其余分量保持不变。但第一个条件依赖于未知参数的真值及正则化参数的选取,不易满足,可操作性不强。
本文基于复共线性诊断理论[14]提出了利用复共线性诊断确定偏差矫正项的截断型岭估计。首先深入分析了岭估计和截断奇异值分解(truncated SVD,TSVD)估计存在的缺陷和不足,结合对复共线性诊断、度量所获得的关键信息,通过引入适当的滤波因子设计基于复共线性诊断的截断型岭估计[15, 16]。其中通过计算每个待估参数的LS估计的信噪比确定截断参数,以均方误差达到最小为目标确定正则化参数,最终得到基于复共线性诊断的截断型岭估计,然后计算其偏差,从中去掉偏差,得到偏差矫正的截断型岭估计。同理,在偏差矫正时,亦应避开趋于零的小奇异值所对应的项,这样使得偏差矫正工作做到精准而有节制,偏差矫正的正则解更稳定,估计更精确。不难看出,本文算法是利用均方误差极小确定正则化参数,由复共线性诊断得到的关键信息确定截断参数及偏差矫正项。即把文献[13]的第一个分析性条件分解成两个过程完成,这样便于计算,易于操作。
1 基于复共线性诊断的偏差矫正的截断型岭估计 1.1 基于复共线性诊断的截断型岭估计
设计阵病态时,其特征值单调地趋于零,使得很小的观测误差导致参数估值较大的误差,因此最小二乘解严重偏离真值。为了深入分析其原因,对设计阵作如下的SVD分解:

其中,U =(u1,…,ut); U T U = I t,V T V = VVT= I t,Λ =diag(λ1,…,λt),λ1≥…≥λt>0为设计阵的非零奇异值。将式(4)展开代入式(3)得:

其中,u i、 v i(i=1,…,t)分别为 U 、 V 的列向量。另外,将观测向量 L 等于真值L 与噪声ε之差的关系式L = L - ε 代入式(5)得:

从式(6)右端可以看出小奇异值对应的观测误差被放大,最终导致最小二乘解不稳定。为了获得稳定的最小二乘解,必须引入适当的滤波因子以抑制小奇异值放大观测误差对最小二乘解的影响。引入滤波因子τi后,得到的参数估值为:
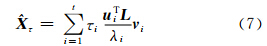
对于不同的滤波因子,就得到形式不同的估计。如对应岭估计的滤波因子为 ,其中h为岭参数。代入式(7)得如下形式的岭估计:
,其中h为岭参数。代入式(7)得如下形式的岭估计:
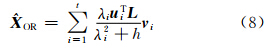
从式(7)看出,岭参数不仅对小奇异值进行了修正,对相对较大的奇异值即模型的可靠部分也进行了修正,有些矫枉过正,致使最小二乘解发生了畸变。对应TSVD正则化的滤波因子为:
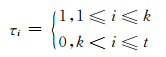
其中,k为截断参数。代入式(7)得到如下形式的TSVD估计:
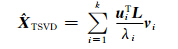
显然,TSVD估计直接删除了小奇异值的对应项,即大污染项,保留大奇异值的对应项不变,以此来消除噪声污染,恢复解的主要特性。但最终导致消除噪声的同时也影响了解的分辨率,致使解的保真效果不好。 对此,本文设计了基于复共线性诊断的截断型岭估计。通过对复共线性诊断、度量及计算各待估参数LS估计的信噪比,确定参数估值受复共线性危害的程度和部位,相应地把设计阵的奇异值分成了相对较大和相对较小的两部分,即模型的可靠部分和不可靠部分。对于不可靠部分,沿用岭估计的做法进行正则化处理。这样既抑制了小奇异值对观测噪声高频段的影响,又避免了模型的可靠部分发生畸变,提高了解的保真效果。由此得到基于复共线性诊断的截断型岭估计的滤波因子为:
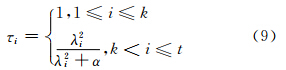
其中,k、α分别为截断参数、正则化参数,均为待定参数。将式(9)代入式(7)得到基于复共线性诊断的截断型岭估计为:

通过计算各待估参数LS估计的信噪比,确定截断参数k。具体做法是:首先计算信噪比估计量,如式(11)所示,将每个待估参数的估计效果区分开来:
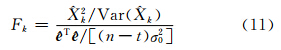
其中,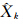 为第k个参数的LS估计;
为第k个参数的LS估计;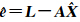 为残差向量。式(11)称为第k个参数Xk的LS估计 k的信噪比估计量。然后利用文献[14]的检验法则:当Fk≤F1,n-r,χ12(γ)(α)时,认为复共线性对相应参数估计 i的危害比较严重,其估计效果不好;当Fk>F1,n-r,χ12(γ)(α)时,认为复共线性对相应参数估计 i的危害比较小,其估计效果较好。其中α为显著性水平;F1,n-r,χ12(γ)(α)是非中心F分布F1,n-r,χ12(γ)的上侧α分位点。实际应用中,阈值的选取可以根据具体情况灵活确定,不必拘泥于由显著性水平所确定的分位点,信噪比检验阈值的不同会使信噪比估计的解算结果产生差异,阈值的具体选取方法可以参阅文献[14]。
为残差向量。式(11)称为第k个参数Xk的LS估计 k的信噪比估计量。然后利用文献[14]的检验法则:当Fk≤F1,n-r,χ12(γ)(α)时,认为复共线性对相应参数估计 i的危害比较严重,其估计效果不好;当Fk>F1,n-r,χ12(γ)(α)时,认为复共线性对相应参数估计 i的危害比较小,其估计效果较好。其中α为显著性水平;F1,n-r,χ12(γ)(α)是非中心F分布F1,n-r,χ12(γ)的上侧α分位点。实际应用中,阈值的选取可以根据具体情况灵活确定,不必拘泥于由显著性水平所确定的分位点,信噪比检验阈值的不同会使信噪比估计的解算结果产生差异,阈值的具体选取方法可以参阅文献[14]。
同时使式(10)估计均方误差达到最小为目标确定正则化参数α,易得式(10)的均方误差为:
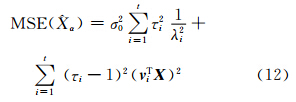
当极小化该均方误差时,σ02用其无偏估计代替,未知参数真值 X 先用LS估计替代,然后用数值迭代的近似值替代。
1.2 对截断型岭估计进行偏差矫正
显然,由式(10)得到的基于复共线性诊断的截断型岭估计是有偏的,其偏差为:

从正则解 α中去掉偏差,得到未知参数的无偏估计:
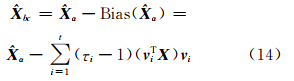
其中,未知参数真值 X 是未知的,借鉴文献[13]的做法,以 代替真值 X 得到完全偏差矫正的有偏估计:
代替真值 X 得到完全偏差矫正的有偏估计:
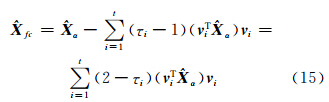
众所周知,趋于零的小奇异值放大噪声对解的污染 是导致LS解不稳定的主要原因,正则化方法是通过引入合适的正则化参数来“镇压”小奇异值,从而达到提高解算估值的效果。从这点来看,偏差矫正时,应该避开小奇异值所对应的项。因为趋于零的小奇异值对应的偏差往往很大,导致偏差矫正之后的有偏估计严重偏离真值,甚至会得到与真值符号相反的估值。因此偏差矫正时,应该避开小奇异值对应的项,最终得到部分偏差矫正的截断型岭估计:
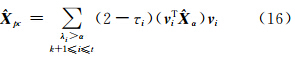
式中,条 件λi>α是为了避开异常小的奇异值;k+1≤i≤t是利用上述确定的截断参数k以限制偏差矫正的范围。部分偏差矫正的估值也是有偏的,其偏差为:
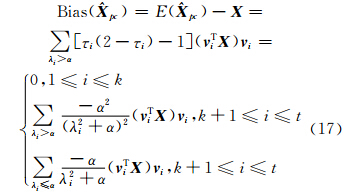
可以看出,若正则化参数取值较小,二阶项会变得更小,甚至可以忽略不计,因此估值的均方误差矩阵可以由协方差矩阵近似代替,即
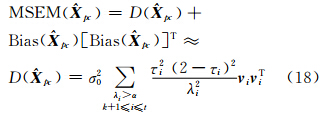
其中,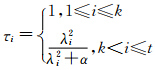 。当求估值均方误差时,σ02用其无偏估计代替。
。当求估值均方误差时,σ02用其无偏估计代替。
应该强调的是,基于复共线性诊断的偏差矫正的截断型岭估计是对式(10)进行偏差矫正,既要结合截断参数k,同时又要满足分析性条件λi>α(i=k+1,…,t)。
2 算例与分析
算例1 考虑一个模拟空间测边网,10个已知点,3个未知点 P11、P12、P13,假设其模拟值分别为(0,0,0)、(14,41,-11)、(68,-26,9)。坐标及其观测距离列于表 1,3个未知点间的观测距离分别为d11,12=44.89 m,d11,13=73.355 m,d12,13=88.34 m。其中观测量为等精度,中误差为0.01 m,要确定3个未知点的9个坐标。若坐标近似值分别取为P11(-0.01,0.02,0.00)、P12(14.02,41.02,-10.98)、P13(68.01,-25.98,8.98),则设计阵 A 的奇异值为3.356 3、2.971 5、 2.828、1.983、1.636 3、1.115 2、0.213 5 、0.060 9、0.021 6,其条件数K( A )=λ1/λ9=155.384 3,法矩阵的条件数约为2.4×104,属于严重病态,其LS估值很不稳定。为了比较各种估计的实际效果,采用以下三种思路进行求解。
| 坐标/m | 观测距离/m | |||||
| x | y | z | di,11 | di,12 | di,13 | |
| P1 | 8.000 | 7.510 | -0.015 | 10.7727 | 35.772 6 | 69.352 3 |
| P2 | - 40.000 | 5.991 | 0.010 | 40.426 0 | 65.271 0 | 112.996 4 |
| P3 | 72.000 | 5.500 | -0.010 | 72.239 8 | 68.894 2 | 33.106 5 |
| P4 | 19.000 | 5.490 | 0.000 | 19.977 3 | 37.539 5 | 58.957 4 |
| P5 | -80.000 | 5.485 | -0.005 | 80.158 7 | 101.185 1 | 151.559 7 |
| P6 | 0.000 | 6.515 | -0.005 | 6.505 0 | 38.848 6 | 75.929 9 |
| P7 | 29.000 | 6.051 | 0.000 | 29.644 4 | 39.501 7 | 51.285 7 |
| P8 | -38.000 | 5.495 | -0.005 | 38.375 2 | 63.927 9 | 110.936 0 |
| P9 | 7.000 | 5.492 | 0.010 | 8.887 3 | 37.839 1 | 69.255 6 |
| P10 | -42.000 | 6.010 | -0.010 | 42.417 8 | 66.900 9 | 114.946 6 |
解法1 岭估计算法,岭参数由Hoerl-Kennard(HK)公式[1]确定:
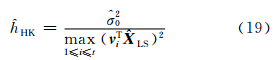
其中 为σ02的无偏估计。
为σ02的无偏估计。
解法2 基于复共线性诊断的截断型岭估计,通过计算LS估计的信噪比估计量(见式(20)),将每个待估参数的估计效果区分开来,
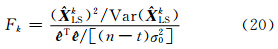
其中,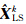 为LS估计的第k个分量;
为LS估计的第k个分量; 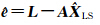 为残差向量。依据文献[14]的具体做法,取阈值d=121.34,显著性水平α=0.05,临界值c=F1,24,121.34(0.05)=71.88,从而确定有3个LS估计的分量所对应的信噪比估值较小,而有6个LS估计的分量所对应的信噪比估值较大,确定截断参数k=6,通过计算式(11)所对应的均方误差MSE(
为残差向量。依据文献[14]的具体做法,取阈值d=121.34,显著性水平α=0.05,临界值c=F1,24,121.34(0.05)=71.88,从而确定有3个LS估计的分量所对应的信噪比估值较小,而有6个LS估计的分量所对应的信噪比估值较大,确定截断参数k=6,通过计算式(11)所对应的均方误差MSE(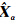 )达到最小,从而确定正则化参数α=0.059。
)达到最小,从而确定正则化参数α=0.059。
解法3 部分偏差矫正的正则化解法,满足条件λi>0.059,避开最小奇异值对应的项进行偏差矫正,计算结果如表 2所示。
| 方案 | x11 | y11 | z11 | x12 | y12 | z12 | x13 | y13 | z13 | MSE |
| 真值 | 0 | 0 | 0 | 14 | 41 | -11 | 68 | -26 | 9 | |
| LS估值 | -0.033 2 | 0.064 8 | 0.799 8 | 14.026 6 | 41.198 9 | -10.340 2 | 67.982 8 | -26.007 4 | 9.258 4 | 10.477 4 |
| 信噪比估值 | 65(*) | 144 | 4 649 | 0(*) | 1 678 | 504 | 26(*) | 114 | 51 262 | |
| 解法1 | -0.030 1 | -0.148 3 | 0.3137 | 14.045 6 | 40.939 2 | -10.795 4 | 67.434 6 | -25.971 7 | 9.92 | 6.702 4 |
| 解法2 | -0.030 8 | -0.147 8 | 0.233 | 14.047 | 40.98 | -10.984 | 67.422 9 | -25.970 9 | 8.919 | 2.997 5 |
| 解法3 | -0.052 1 | -0.026 8 | 0.477 5 | 14.03 | 40.925 | -10.884 3 | 67.327 | -25.947 | 8.912 4 | 0.759 2 |
算例2 若坐标近似值分别取为P11(0.20,0.15,0)、P12(14.12,40.89,-11.20)、P13(68.15,-25.89,8.93),设计阵的奇异值为3.357 2、2.967 1、2.822 9、1.988 3、1.649 4、1.111 1、0.218 3、0.031、0.01,其条件数K(A )=λ1/λ9=335.72,法矩阵的条件数为1.127×105,属于严重病态。相应的计算结果列于表 3。
| 方案 | x11 | y11 | z11 | x12 | y12 | z12 | x13 | y13 | z13 | MSE |
| 真值 | 0 | 0 | 0 | 14 | 41 | -11 | 68 | -26 | 9 | |
| LS估值 | -0.012 7 | -0.099 7 | 0.452 5 | 14.189 7 | 39.363 4 | -16.646 | 67.98 | -25.502 3 | 11.059 2 | 47.570 9 |
| 信噪比估值 | 0.128(*) | 0.027 8(*) | 778 | 0.027 8(*) | 232 | 2 833 | 0.162 8(*) | 1 445 | 5 397 | |
| 解法1 | 0.066 8 | 0.109 7 | 0.502 4 | 14.100 3 | 41.509 8 | -10.896 8 | 68.025 1 | -25.583 | 8.726 9 | 40.272 5 |
| 解法2 | 0.2749 | 0.092 5 | -0.229 2 | 14.191 6 | 40.605 7 | -11.165 5 | 68.264 6 | -26.154 8 | 9.131 6 | 22.529 3 |
| 解法3 | 0.2465 | 0.001 8 | -0.006 4 | 14.222 4 | 40.956 5 | -11.070 3 | 68.115 1 | -26.124 | 9.135 3 | 0.783 0 |
分析表 1、表 2中的解算结果可知,当解算模型的设计矩阵病态时,由各种算法得到的结果不同。
1) LS估计的均方误差很大,致使估值偏离真值,解极不稳定。
2) 以上思路均可以有效地改善LS估计的精度。
3) 解法3得到的估值的均方误差最小,精度最好,说明估计效果较好,有效地改进了LS估计的精度,提高了参数估值的准确性和稳定性。
4) 解法3得到的估值的均方误差虽然仍是最小的,但显然也受到坐标近似值近似程度的影响,当近似程度不太好时,得到的均方误差偏大。总的来说,解法3的估计效果是值得肯定的,它显著提高了参数估值的稳定性和有效性。
3 结 语
本文提出的偏差矫正的截断型岭估计巧妙地结合了一般的偏差理论和由复共线性诊断、度量与检验所获得的关键信息,且有针对性地克服了复共线性的危害,减弱了有偏估计的偏差所造成的影响。从算例可以看出,该算法在均方误差意义下大大提高了解算质量。同时该方法所要求的分析性条件容易满足,在解决实际问题时便于操作,具有较好的适用性。
| [1] | Hoerl A E,Kennard R W. Ridge Regression:Biased Estimation for Non-Orthogonal Problems[J].Technometrics,1970,12:55-67 |
| [2] | Liu K. A New Class of Biased Estimate in LinearRegression[J].Communications in Statistics-Theory and Methods,1993,22(2):393-402 |
| [3] | Gui Qingming,Li Guozhong.Combining Ridge and Shrunken Estimator and Its Applications in Geodetic Adjustment[J].Journal of Geodesy and Geodynamics,2002,22(1):16-21(归庆明,李国重.岭-压缩组合估计及其在测量中的应用[J].大地测量与地球动力学,2002,22(1):16-21) |
| [4] | Gui Qingming,Li Guozhong,Ou Jikun. Combining Ridge and Principal Component Estimator and Its Application in Geodetic Adjustment[J]. Engineering of Surveying and Mapping,2002,11(4):11-13(归庆明,李国重,欧吉坤.岭-主成分组合估计及其在测量平差中的应用[J].测绘工程,2002,11(4):11-13) |
| [5] | Liu K. Moreon Liu-Type Estimator in Linear Regression[J].Communications in Statistics-Theory and Methods,2004,33(11):2 723-2 733 |
| [6] | Jadhav N H,Kashid D N. A Jackknifed Ridge M-Estimator for Regression Model with Multicollinearity and Outliers[J].Journal of Statistical Theory and Practice,2011,5(4):659-673 |
| [7] | Ozkale M R. A Jackknifed Ridge Estimator in the Linear Regression Model with Heteroscedastic or Correlated Errors[J].Statistics and Probability Letters,2008,78(18):3 159-3 169 |
| [8] | Ozkale M R,Kaciranlar S.The Restricted an Unrestricted Two-Parameter Estimators[J].Communications in Statistics-Theory and Methods,2007,36(15):2 707-2 715 |
| [9] | Xu Jianwen.Research on Restricted Biased Estimation and Preliminary Test Estimation of Parameters in Linear Models[D].Chongqing:Chongqing University,2009(徐建文.线性模型参数的约束有偏估计和预检验估计研究[D].重庆:重庆大学,2009) |
| [10] | Gui Qingming, Guo Jianfeng. Study on Methods for Solving Ill-conditioned Equations[J].Journal of Geodesy and Geodynamics, 2004,24(3):15-18(归庆明,郭建锋. 病态平差模型直接解算方法的研究[J].大地测量与地球动力学,2004,24(3):15-18) |
| [11] | Xu P L,Shen Y Z,Fukuda Y,et al. Variance Component Estimation in Linear Inverse Ill-Posed Models[J].J Geod, 2006, 80(2):69-81 |
| [12] | Xu P L. Iterative Generalized Cross-Validation for Fusing Heteroscedastic Data of Inverse Ill-Posed Problems[J].Geophys J Int,2009,179(1):182-200 |
| [13] | Shen Y Z,Xu P L,Li B F. Biased-Corrected Regularized Solution to Inverse Ill-Posed Models[J].J Geod, 2012,86(8):597-608 |
| [14] | Gu Yongwei. Regularization Methods Based on Multicollinearity Diagnosis and Their Applications to Geodesy[D]. Zhengzhou:Information Engineering University,2010(顾勇为.基于复共线性诊断的正则化方法及其在大地测量中的应用[D].郑州:信息工程大学,2010) |
| [15] | Gui Qingming,Guo Jianfeng.A New Ambiguity Resolution Based on Paritial Ridge Estimator[J].Journal of Information Engineering University,2004,5(2):137-139(归庆明,郭建锋.部分岭估计在整周模糊度解算中的应用[J].信息工程大学学报,2004,5(2):137-139) |
| [16] | Gu Yongwei.Study of Regularization Based on Signal-to-Noise Index in Airborne Gravity Downward to the Earth Surface[J].Acta Geodaetica et Cartographica Sinica,2010,39(5):458-464(顾勇为.航空重力测量数据向下延拓基于信噪比的正则化方法的研究[J].测绘学报,2010,39(5):458-464) |
 2015, Vol. 40
2015, Vol. 40


