文章信息
- 王德军, 熊永良, 徐韶光
- WANG Dejun, XIONG Yongliang, XU Shaoguang
- 利用窗口小波去噪的高精度动态单历元定位算法
- A Precise Kinematic Single Epoch Positioning Algorithm Using Moving Window Wavelet Denoising
- 武汉大学学报·信息科学版, 2015, 40(6): 779-784
- Geomatics and Information Science of Wuhan University, 2015, 40(6): 779-784
- http://dx.doi.org/10.13203/j.whugis20130636
-
文章历史
- 收稿日期:2013-11-01
2. 河北工业大学测绘工程系, 天津 300401;
3. 河北省土木工程技术研究中心, 天津 300401
2. Department of Surveying Engineering, Hebei University of Technology, Tianjin 300401, China;
3. Civil Engineering Technology Research Center of Hebei Province, Tianjin 300401, China
在短基线定位情况下,定位精度主要受测量噪声和多路径的影响。为提高定位精度,可采用小波分析进行去噪处理,文献[1, 2, 3]将强制小波去噪应用于变形监测中,该方法保留信号层的小波分解低频系数,部分高频系数置零,这样容易丢失信号中的有用成分;文献[4, 5]采用阈值去噪,处理结果受分解层数、阈值函数、阈值大小的影响较大;文献[6, 7]利用经验模态分解(empirical mode decomposition,EMD)滤波消弱噪声,并根据多路径的周日重复性建立改正模型;钟萍等人[8]将交叉证认法与Vondrak滤波器相组合实现信噪合理分离,达到提高定位精度的目的。
上述在提高精度方面的研究大多是在静态情况下开展的,此时可利用多路径的重复性建立改正模型,戴吾蛟等人的研究表明,天线至信号反射面的距离即使只有1 cm的微小变化,也将引起多路径效应较大的变化,此时利用重复性模型改正多路径可能会引入新的误差[9]。文献[10]的研究认为,动态定位下的多路径由两部分构成,一部分由流动站产生,由于流动站的运动,由其产生的多路径可以认为被随机化,进而当做偶然误差通过滤波来处理;另一部分为由基站产生的低频多路径,其在天与天之间仍有重复性。文献[5]利用窗口小波对动态观测的双差数据去噪,低频多路径得到了极大的消弱,模糊度解算的可靠性和精度都得到提高。
本文提出了一种基于窗口小波去噪的高精度动态单历元定位算法,该算法利用窗口小波对当前历元观测值残差去噪,通过交叉证认实现小波去噪分解层数的自适应选取。本算法针对列车在轨动态运行的特点,通过附加轨迹约束进行单历元解算,利用宽巷组合波长较长、模糊度比较容易固定的特点,首先固定宽巷模糊度,再利用宽巷模糊度和轨道约束条件,分别固定L1、L2模糊度并进行平差,解算得到观测值残差;当观测历元的个数达到窗口宽度时,利用小波对L1、L2双差观测值残差进行去噪,为防止端部效应,通过比较,选择适合动态解算的延拓方案,在当前历元右侧进行延拓,对延拓后的残差值序列去噪后,从中提取去噪后的残差与原始观测值相加,得到较为干净的观测值,重新解算第一个窗口内所有历元的坐标;之后,观测值每增加一个历元,窗口也随之移动一个历元,在当前历元右侧延拓。与第一个窗口不同的是,去噪后只更正当前历元的双差观测值;利用去噪后的观测值计算当前历元的最终定位结果,可满足动态情况下的实时解算。
1 数学模型 1.1 附加轨迹约束的单历元解算算法
将伪距差分平差后的未知数平差值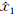 作为一组权为 PX1的虚拟观测值[11],与轨迹约束条件、宽巷双差相位观测值一起解算[12],根据平差结果,用LAMBDA方法固定宽巷模糊度。在宽巷模糊度固定后,根据N W= N L1- NL2,将L1、L2观测值的误差 方程表达为只含有L1模糊度 N L1的形式。结合约束条件[13, 14, 15, 16],得到如下数学模型:
作为一组权为 PX1的虚拟观测值[11],与轨迹约束条件、宽巷双差相位观测值一起解算[12],根据平差结果,用LAMBDA方法固定宽巷模糊度。在宽巷模糊度固定后,根据N W= N L1- NL2,将L1、L2观测值的误差 方程表达为只含有L1模糊度 N L1的形式。结合约束条件[13, 14, 15, 16],得到如下数学模型:
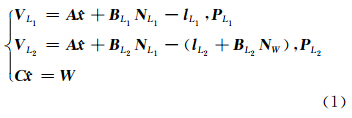
式中,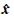 为坐标改正数; N L1、 N W分别为L1、LW的模糊度向量; A 为坐标改正数系数阵; B L1、 B L2为L1、L2双差模糊度对应的系数阵; l L1、 l L2分别为L1、L2双差观测值与计算值的差值; P L1、 P L2分别为L1、L2双差观测值的权阵。其法方程为:
为坐标改正数; N L1、 N W分别为L1、LW的模糊度向量; A 为坐标改正数系数阵; B L1、 B L2为L1、L2双差模糊度对应的系数阵; l L1、 l L2分别为L1、L2双差观测值与计算值的差值; P L1、 P L2分别为L1、L2双差观测值的权阵。其法方程为:
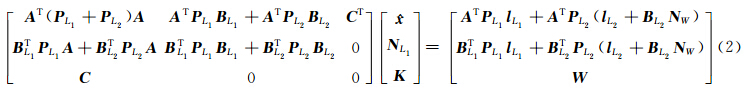
用LAMBDA方法将L1模糊度固定后,回代到误差方程中,重新组成法方程,得到最终坐标。
1.2 窗口小波去噪
去噪效果与小波基、阈值函数、阈值、分解层数的选取有关。小波基的选择大多通过试算得到,本文根据文献[5],所选的小波基为sym8,阈值函数选择硬阈值。阈值的选择相对较宽松,阈值在一定范围内变化时,通常不会导致去噪效果有较大的变化[17],本文对每层小波系数分别计算中误差,并以3倍中误差作为本层的阈值[17]。对去噪效果影响最大的是分解层数,分解层数多,容易造成信号信息丢失严重;分解层数少,则消噪效果不理想。文献[5]在用窗口小波去噪时,未对影响去噪效果的小波的分解层数做出讨论,本文将交叉证认法[6, 18]应用于窗口小波去噪中,通过交叉证认构造的最小均方误差目标函数实现分解层数的自适应选取,并实现动态处理。其基本过程如下。
1) 对当前历元的观测数据按常规单历元方法处理,得到双差观测值残差,当历元的个数达到窗口宽度时,在其右侧进行延拓,对延拓后的观测值序列进行去噪。
2) 将 w个观测序列(ti,si)分为奇序列(t1,2m-1,s1,2m-1)和偶序列(t2,2m,s2,2m)两个样本,m=1,2,…,n1(w为偶数时,n1=w/2;w为奇数时,n1=(w-1)/2),将奇数样本作为滤波样本,从偶数样本中进行随机抽样作为证认样本,实验中抽取的样本个数n2=0.2w。
3) 选取初始分解层数l和小波基,对滤波样本进行小波变换,对每层的小波系数独立地确定一个阈值,利用硬阈值函数进行处理,得到新的小波系数;进行小波逆变换,得到奇序列去噪后的信号f′。
4) 计算证认样本对滤波值的方差:
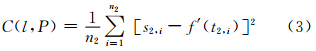
式中,f′(t2,i)是由滤波值f′对应于证认样本的时间t2,i由三次样条插值内插得到的;P表示对偶序列的一次随机划分。
5) 对偶序列进行M次不同的随机划分,考虑到统计特性和计算效率,本次实验中M=20,得到M次划分的方差,并计算其均值:
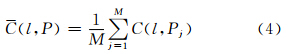
6) 选取不同的分解层数,重复步骤2)、3)、4),方差均值C(l,P)最小时对应的l即为最佳分解层数。由于信号长度和小波基确定了能分解的最大层数,在达到最大分解层数时停止计算。
7) 由于滤波样本的采样率为原始观测序列采样率的一半,则原始观测序列的最佳分解层数为l+1,据此对原始观测序列去噪得到滤波序列,对双差观测值修正,并用其解算窗口内所有历元的最终坐标。
8) 随着观测历元的增加,窗口随之滑动,重复步骤2)到7),对于当前历元t的残差的去噪,只用到了从历元t-width+1到历元t之间的残差序列(width为窗口的宽度),在当前历元的右侧进行对称延拓,将延拓之后的数据小波去噪后,提取当前历元去噪后的残差数据,用其修正原始双差观测值,并解算去噪后的当前历元的坐标,实现实时动态处理。
考虑到采用交叉证认法对数据序列划分的需要和解算的实时性,在本文中,窗口宽度取为512。笔者尝试过1 024、2 048等窗口宽度,其对最终的处理结果几乎没有影响,但每个窗口选取的分解层数不一样,这也从一个方面说明交叉证认法的自适应性。另外,在计算过程中,为防止端部效应对选取最佳分解层数的影响,仅选取资料序列中部约70%的数据进行计算。 2 算例分析
本文实验在河北工业大学教师公寓楼顶进行,接收机为合众思壮E660,采样间隔为0.2 s,基站与流动站的距离大约为20 m,如图 1所示,周围都有较强的反射物,流动站被安置在长约2.5 m的直线轨道上,进行连续三天的数据采集,第一天以0.12 m/s的速度在轨道上来回运动,第二天以0.20 m/s的速度来回运动,第三天以0.48 m/s的速度来回运动。设相邻两天的相关延迟为236 s,连续三天观测的相同时间段的时长为27 min 21.8 s,共采集8 210个历元。

|
| 图 1 实验中基站和流动站的分布 Fig. 1 Layout of Base and Rover Stations for the Experiment |
残差序列为有限长信号,小波分解与重构中的卷积运算必然涉及到边界延拓[19],不同的延拓方法会产生不同的端部效应。当前历元的残差数据处于窗口的最右端,受端部效应的影响最大,本文以小波后处理的观测值残差结果为参照,对补零延拓(zpd)、周期延拓(ppd)、对称延拓(sym)、0阶平滑延拓(sp0)和1阶平滑延拓(sp1)等几种延拓方法做出比较,选择最适合动态数据处理的延拓方案。
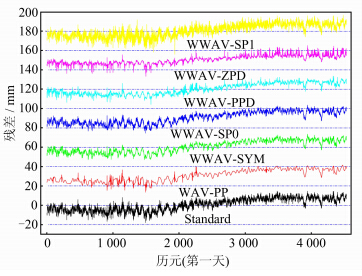
连续两天的有效卫星观测数为8颗,以高度角最大的31号卫星为参考星,组成7个双差观测值,按单历元进行计算,得到原始双差观测值残差(记为Standard模式),将此残差利用窗口小波去噪,延拓模式分别采用了对称延拓、0阶平滑延拓、周期延拓、补零延拓和1阶平滑延拓,得到去噪后的残差序列,分别记为WWAV-SYM、 WWAV-SP0、WWAV-PPD、WWAV-ZPD、WWAV- SP1模式。对原始双差观测值序列做小波后处理,记为WAV-PP模式。由于在计算过程中高度角设置为10°,23号卫星的高度角最小,在前1 744个历元,其高度角小于10°,未参与解算,残差未能给出,共6 466个历元。在以WAV-PP模式处理时,为防止端部效应的影响,提取其中间70%的数据作为其他处理模式的参照。图 2为第一天23号卫星L1观测值残差,为显示方便,图中将各种模式下去噪后的残差序列分别上移了30 mm。
从图 2可以看出,相对于其他几种处理模式,原始残差序列(Standard)采用小波后处理(WAV-PP)后,高频部分得到最好的消弱,WWAV-SP1则引入了更多的噪声,其他两天也有类似的情形。表 1统计了五种延拓模式以后处理的结果为参照的RMS值,可以看出,WWAV-SYM和WWAV-SP0对应的RMS值相对较小,与后处理的结果较为吻合。
|
| 图 2 PRN31-23的L1载波相位双差观测值在标准模式和窗口小波去噪下的残差 Fig. 2 Carrier-Phase DD Residuals of PRN31-23 in the Standard and WWAV Strategies |
| WWAV-SYM | WWAV-SP0 | WWAV-PPD | WWAV-ZPD | WWAV-SP1 | |
| 第一天 | 1.38 | 1.41 | 1.92 | 2.52 | 2.85 |
| 第二天 | 1.33 | 1.39 | 2.11 | 2.78 | 3.41 |
| 第三天 | 1.74 | 1.88 | 2.15 | 2.82 | 4.37 |
本文在用WWAV-SYM模式处理L1双差观测值残差时,第一天所有窗口的平均分解层数为3.16,第二天所有窗口的平均分解层数为3.47,第三天所有窗口的平均分解层数为3.58,自适应了运动速度快时噪声较大的特点。
为检验连续三天残差的重复性,表 2给出了标准模式(Standard)、后处理模式(WAV-PP)、对称延拓模式(WWAV-SYM)、0阶平滑延拓模式(WWAV-SP0)下残差的相关系数。可以看出,后处理后,其相关性最高,对称延拓模式和0阶平滑延拓模式下,其相关性也得到进一步提高,这种相关性主要反映的是基站的多路径的重复性。第二天与第三天的相关性低于第一天与第三天的相关性,可能与第二天和第三天的运动速度较快、噪声较大有关。笔者也计算了其他6个双差观测值残差连续三天之间的相关系数,都未超过PRN31-23双差观测值残差的相关系数,其相关系数大多在0.5左右,低于静态模式下观测值残差的相关系数,这为动态模式下利用多路径的重复性建立坐标改正模型带来了困难。
| Day | Standard | WAV-PP | WWAV-SYM | WWAV-SP0 |
| 1~2 | 0.762 | 0.855 | 0.837 | 0.829 |
| 2~3 | 0.652 | 0.784 | 0.765 | 0.744 |
| 1~3 | 0.698 | 0.832 | 0.797 | 0.780 |
考虑到WWAV-SYM和WWAV-SP0延拓模式下残差处理效果较好,在随后的窗口小波坐标解算中主要考虑这两种延拓方案。本文也采用了Kalman滤波做动态处理,与窗口小波的处理结果进行对比。文中采用了中间70%的数据来进行分析(5 748个历元),设计了以下五种方案进行解算:① 直接采用L1、L2 双差观测数据按照常规单历元方法解算。② 在方案①的基础上,对残差采用小波后处理去噪,用去噪后的残差修正原始观测值,再次进行解算。③ 在方案①的基础上,对得到的L1、L2双差观测数据的残差进行窗口小波去噪,采用WWAV-SYM延拓模式,用去噪后的残差修正原始观测值,再次进行解算。④ 与方案③类似,所不同的是采用了WWAV-SP0延拓模式。⑤ 采用了Kalman滤波做动态处理。
为得到精确的轨迹方程,接收机在直线轨道上静态采集了两个点,两点采集时间超过4 h,在固定基站坐标下,得到该两点的坐标如表 3所示,高斯平面坐标系下的坐标是在中央子午线117°03′00″、投影高程面为28.7 m的设置下投影得到的。短基线情况下,定位结果主要受测量噪声和多路径的影响,而在长时间观测下,多路径和噪声能得到较好的平滑,可视A、B两点的坐标为真实坐标。用水准测量的方法施测了A、B两点的高差与表 3中的大地高高差相比也是吻合的,最终确定出轨道的坡度是1.18%。
| 点名 | x | y | h |
| A | 4 344 387.733 8 | 499 821.625 0 | 30.573 4 |
| B | 4 344 386.558 7 | 499 822.048 9 | 30.571 9 |
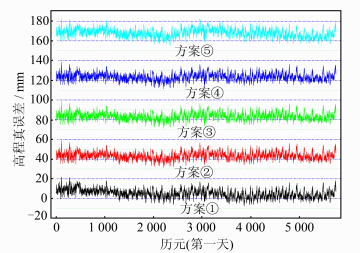
由于实验条件的限制,未能获得每个历元的精确平面坐标,通过每个历元在投影平面上偏离直线AB的距离来评估其平面精度(下文简称为平面偏差)。AB的坡度较小,通过每个历元的平面坐标计算出其距端点的距离,可以较为准确地内插出其高程,将其视为真值来评估高程的精度。图 3是第一天的高程真误差,为显示方便,将其他方案的h真误差分别向上平移了40 mm。
|
| 图 3 第一天的高程真误差 Fig. 3 True Error of Height in First Day |
表 4统计了连续三天五种不同方案的平面偏差序列和高程真误差序列的RMS值,在第一天,方案①的平面偏差RMS值为2.65 mm,h为6.54 mm左右;在第二天和第三天,其RMS值出现一定程度的增加,这可能与随着流动站运动速度的提高,周围环境变化快,导致多路径误差快速变化有关。采用两种不同延拓方式的窗口小波处理结果与小波后处理结果非常一致,采用Kalman滤波处理的结果(方案⑤)比常规单历元的结果(方案①)还要差,这可能是由于动态测量时测量噪声大,之前历元的数据对当前历元的精度没有起到改善作用。
| Day | 方案 | 平面/mm | 提高百分比/% | 高程/mm | 提高百分比/% |
| ① | 2.65 | - | 6.54 | - | |
| ② | 2.26 | 14.72 | 4.95 | 24.31 | |
| 1 | ③ | 2.24 | 15.47 | 4.98 | 23.85 |
| ④ | 2.25 | 15.09 | 4.96 | 24.16 | |
| ⑤ | 2.94 | -10.94 | 8.86 | -35.47 | |
| ① | 2.64 | - | 7.79 | - | |
| ② | 2.21 | 16.29 | 6.06 | 22.21 | |
| 2 | ③ | 2.19 | 17.05 | 6.04 | 22.46 |
| ④ | 2.20 | 16.67 | 6.05 | 22.34 | |
| ⑤ | 2.86 | -8.33 | 9.96 | -27.86 | |
| ① | 2.86 | - | 8.19 | - | |
| ② | 2.33 | 18.53 | 6.28 | 23.32 | |
| 3 | ③ | 2.30 | 19.58 | 6.28 | 23.32 |
| ④ | 2.31 | 19.23 | 6.25 | 23.69 | |
| ⑤ | 3.26 | -13.99 | 10.83 | -32.23 | |
| 注: RMS改善的百分比是相对于当天的第一种方案计算得到的。 | |||||
在基站多路径的影响下,其残差序列具有一定的重复性,为检验其真误差序列是否也具有一定的重复性,计算了方案③的相邻两天的高程真误差的相关系数。第一天与第二天的相关系数为0.079,第二天与第三天的相关系数为0.114,其相关性都不高,这主要是由于真误差是受到残差的综合影响,而残差序列的相关性本身就不高,必然导致真误差的相关性不高。 3 结 语
1) 通过交叉证认自适应地选择最佳分解层数,利用窗口小波对残差去噪,去噪效果受窗口长度的影响不大。在接收机以0.48 m/s运动的情况下,利用方案③得到平面偏差的RMS为2.30 mm,h方向的RMS为6.28 mm,比方案①有了明显的提高。
2) 采用对称延拓或者0阶延拓对端部效应有比较好的改善,与小波后处理结果较为一致。
3) 动态定位情况下,其观测值残差序列仍然有一定的重复性,由于流动站的快速移动,导致重复性不高,这种重复性主要反映的是基站多路径的重复性。由于最终的坐标受到多个残差的综合影响,导致坐标真误差序列的重复性很差,此时利用天与天之间的重复性改正可能会引入更多的误差。
4) 如何提高高程方向上的定位精度,以便拓展动态单历元定位的应用领域,是下一步将要开展的工作。
| [1] | Xiong Yongliang, Ding Xiaoli, Huang Dingfa, et al. Integrated Single Epoch Algorithm Based on Wavelet Transform and Its Application to Structural Vibration Monitoring[J]. Acta Geodaetica et Cartographica Sinica,2005, 34(3):202-207(熊永良, 丁晓利, 黄丁发, 等. 基于小波变换的单历元算法及其在结构振动监测中的应用研究[J]. 测绘学报, 2005, 34(3):202-207) |
| [2] | Zhong P, Ding X L, Zheng D W. Adaptive Wavelet Transform Based on Cross-validation Method and Its Application to GPS Multipath Mitigation[J]. GPS Solut, 2008,12(2):109-117 |
| [3] | Huang Shengxiang, Li Peihong, Yang Baocen, et al. Study on the Characteristics of Multipath Effects in GPS Dynamic Deformation Monitoring[J]. Geomatics and Information Science of Wuhan University, 2005, 30(10):877-880(黄声享, 李沛鸿, 杨保岑, 等. GPS动态监测中多路径效应的规律性研究[J]. 武汉大学学报·信息科学版, 2005, 30(10):877-880) |
| [4] | Souza E M, Monico J F G. Wavelet Shrinkage:High Frequency Multipath Reduction from GPS Relative Positioning[J]. GPS Solut, 2004, 8(3):152-159 |
| [5] | De Souza E M, Monico J F G, Polezel W G C, et al. Spectral Analysis and Low-Frequency Multipath Mitigation for Kinematic Applications[C]. Proceedings of the IEEE/ION PLANS, Monterey, CA,2008 |
| [6] | Luo Feixue, Dai Wujiao, Wu Xixiu. EMD Filtering Based on Cross-Validation and Its Application in GPS Multipath[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4):450-453 (罗飞雪, 戴吾蛟, 伍锡锈. 基于交叉证认的EMD滤波及其在GPS多路径效应中的应用[J]. 武汉大学学报·信息科学版, 2012, 37(4):450-453) |
| [7] | Dai Wujiao, Ding Xiaoli, Zhu Jianjun, et al. EMD Filter Method and Its Application in GPS Multipath[J]. Acta Geodaetica et Cartographica Sinica,2006, 35(11):321-327(戴吾蛟, 丁晓利, 朱建军, 等. 基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用[J]. 测绘学报, 2006, 35(11):321-327) |
| [8] | Zhong Ping, Ding Xiaoli, Zheng Dawei. Study of GPS Multipath Effects with Method of CVVF[J]. Acta Geodaetica et Cartographica Sinica,2005, 34(2):161-167(钟萍, 丁晓利, 郑大伟. CVVF方法用于GPS多路径效应的研究[J]. 测绘学报, 2005, 34(2):161-167) |
| [9] | Dai Wujiao, Ding Xiaoli, Zhu Jianjun. Study on Multipath Effect in Structure Health Monitoring Using GPS[J]. Journal of Geodesy and Geodynamics, 2008, 28(1):65-71(戴吾蛟, 丁晓利, 朱建军. GPS动态变形测量中的多路径效应特征研究[J]. 大地测量与地球动力学, 2008, 28(1):65-71) |
| [10] | Zhang Q J, Schwarz K P. Estimating Double Difference GPS Multipath Under Kinematic Conditions[C]. IEEE Position Location and Navigation Symposium, Atlanta, GA, 1996 |
| [11] | Liu Genyou, Ou Jikun. Kinematic Positioning Algorithm with Coordinate Function Constraint[J].Geomatics and Information Science of Wuhan University, 2004, 29(5):389-393(刘根友, 欧吉坤. 具有坐标函数约束的动态定位算法[J]. 武汉大学学报·信息科学版, 2004, 29(5):389-393) |
| [12] | Zhu Huizhong, Gao Xingwei, Xu Aigong, et al. Single-Epoch Ambiguity Resolution for Network RTK Rovers[J]. Science of Surveying and Mapping, 2010, 35(2):77-79(祝会忠, 高星伟, 徐爱功, 等. 网络RTK流动站整周模糊度的单历元解算[J]. 测绘科学, 2010, 35(2):77-79) |
| [13] | Xiong Yongliang, Huang Dingfa, Zhang Xianzhou. A Reliable GPS Single Epoch Processing Algorithm with Known Deformation Interval Constraints[J]. Geomatics and Information Science of Wuhan University, 2001, 26(1):51-56(熊永良, 黄丁发, 张献洲. 一种可靠的含有约束条件的GPS变形监测单历元求解方法[J]. 武汉大学学报·信息科学版, 2001, 26(1):51-56) |
| [14] | Han Baomin, Ou Jikun. A GPS Single Epoch Phase Processing Algorithm with Constraints for Single-frequency Receiver[J]. Acta Geodaetica et Cartographica Sinica,2002, 31(4):300-304(韩保民, 欧吉坤. 一种附约束的单频单历元GPS双差相位解算方法[J]. 测绘学报, 2002, 31(4):300-304) |
| [15] | Dai Wujiao, Zhu Jianjun, Ding Xiaoli, et al. Single Epoch Ambiguity Resolution in Structure Monitoring Using GPS[J]. Geomatics and Information Science of Wuhan University, 2007, 32(3):234-241(戴吾蛟, 朱建军, 丁晓利, 等. GPS建筑物振动变形监测中的单历元算法研究[J]. 武汉大学学报·信息科学版, 2007, 32(3):234-241) |
| [16] | Tang Weiming, Sun Hongxing, Liu Jingnan. Ambiguity Resolution of Single Epoch Single Frequency Data with Baseline Length Constraint Using LAMBDA Algorithm[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5):444-446(唐卫明, 孙红星, 刘经南. 附有基线长度约束的单频数据单历元LAMBDA方法整周模糊度确定[J]. 武汉大学学报·信息科学版, 2005, 30(5):444-446) |
| [17] | Zhang Jixian, Zhong Qiuhai, Dai Yaping. The Determination of the Threshold and the Decomposition Order in Threshold De-noising Method Based onWavelet Transform[J]. Proceedings of the CSEE, 2004, 24(2):118-122(张吉先, 钟秋海,戴亚平. 小波门限消噪法应用中分解层数及阈值的确定[J]. 中国电机工程学报, 2004, 24(2):118-122) |
| [18] | Zhong Ping, Ding Xiaoli, Zheng Dawei, et al. An Adaptive Wavelet Transform Based on Cross-validation and Its Application to Mitigate Multipath Effects[J]. Acta Geodaetica et Cartographica Sinica,2007, 36(3):279-285(钟萍, 丁晓利, 郑大伟, 等. 一种基于交叉证认技术的自适应小波变换及其在消减GPS多路径误差中的应用[J]. 测绘学报, 2007, 36(3):279-285) |
| [19] | Donoho D L, Johnstone I M.Wavelet Shrinkage:Asymptopia[J]. Journal of Royal Statistics Society Series (B),1995, 57:301-369 |
 2015, Vol. 40
2015, Vol. 40


