文章信息
- 周波阳, 罗志才, 宁津生, 肖玉刚
- ZHOU Boyang, LUO Zhicai, NING Jinsheng, XIAO Yugang
- 航空矢量重力测量中有限冲激响应低通数字滤波器的设计
- Design of FIR Lowpass Digital Filters for Airborne Vector Gravimetry
- 武汉大学学报·信息科学版, 2015, 40(6): 772-778
- Geomatics and Information Science of Wuhan University, 2015, 40(6): 772-778
- http://dx.doi.org/10.13203/j.whugis20130089
-
文章历史
- 收稿日期:2013-05-02
2. 武汉大学测绘学院, 湖北 武汉 430079;
3. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China
随着高灵敏性、高稳定性加速度计和陀螺仪及动态差分技术的广泛应用,以及计算机软硬件性能的大幅提升,基于GNSS/SINS(捷联惯导系统)的航空标量和矢量重力测量成为当前大地测量学的热点研究方向[1, 2]。对基于GNSS/SINS的航空重力测量系统来说,不论最终输出的是标量重力还是矢量重力,高精度地测定惯性加速度是获取飞行高度处高精度和高分辨率重力观测数据的关键。
在基于GNSS/SINS的航空重力测量中,惯性加速度由GNSS位置时间序列通过位置差分进行求解,或由GNSS载波相位数据通过相位差分进行求解[3]。由于观测误差的影响及差分过程对噪声的放大,直接由GNSS观测数据导出的载体速度和加速度往往含有大量高频噪声,因此,必须对差分结果作低通滤波处理。国内外学者在航空重力测量中低通滤波器的设计方面取得了一系列研究成果,运用比较广泛的低通滤波器有迭代高斯低通滤波器[4]、IIR数字低通滤波器[5, 6],以及将差分和低通滤波结合在一起的低通差分器[7]。这些研究成果往往专注于航空标量测量数据处理,即载体垂直加速度的低通滤波。与标量重力测量相比,航空矢量重力测量获取的是载体三个方向的加速度,水平加速度的滤波处理也是获取高精度重力矢量数据的关键环节。有限冲激响应(finite impulse response,FIR)数字滤波器可以设计成线性相位,并且数值计算总是稳定的,因此成了航空重力测量中最重要的一类滤波器[7]。FIR数字滤波器的设计主要是建立在对理想滤波器的频率特性作某种近似的基础上的,本文采用窗函数法和最佳一致逼近法设计了两类FIR数字低通滤波器,采用模拟数据来验证滤波器的性能,并结合GPS静态测量数据讨论其在确定载体速度矢量和加速度矢量方面的应用。
1 载体速度和加速度的确定
牛顿插值差分法广泛应用于由GNSS位置时间序列求解载体的速度和加速度。徐天河[8]对牛顿插值数值差分公式的精度进行了较为详细的分析和讨论;钟波[9]比较了三、五、七、九点插值模型,综合考虑计算精度和观测误差的影响,认为七点或九点插值比较适合于位置差分计算;王潜心等[10]研究了牛顿插值一阶差分模型的传播误差与截断误差,认为采用牛顿中心插值最佳点数N的选取在9附近。因此,本文仅以七点牛顿插值模型为例进行讨论,其一阶差分公式为[11]:

式中,Δt为时间间隔。
加速度可由速度再次差分得到,也可以直接通过对位置作牛顿插值二阶差分来获取。考虑到Coriolis及Etvs效应都与载体速度相关[2],本文采取位置差分求解载体的速度,再由速度差分求解加速度。
2 FIR低通滤波器的设计
理想低通滤波器在物理上无法实现,人们通常采用一定的方法来进行逼近,如窗函数法和切比雪夫逼近法等。
2.1 窗函数法
窗函数法的设计思想是用一个有限时宽的 h(n)去逼近理想低通滤波器的冲激响应hd(n),从而使所设计的系统频响H(ejω)逼近理想低通滤波器的幅响Hd(ejω)。在窗函数设计中,h(n)与hd(n)的关系可记为:

式中,w(n)为窗函数。在FIR数字滤波器窗函数设计中,需要选择合适的窗函数w(n)。凯塞窗是一种可以调整主瓣宽度与旁瓣抑制之间交换关系的窗函数,因此本文采用凯塞窗函数,其数学表达式为[12]:

式中,I0(\5)为零阶第一类贝塞尔函数;β为调整窗函数形状的参数。β的值与阻带最小衰减As(dB)有关:
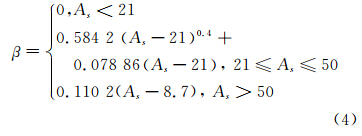
设滤波器的通带截止频率为ωp,阻带截止频率为ωs,令Δω=ωs-ωp,滤波器阶数可表示为[11]:

依据窗函数法的设计指标,即滤波器长度M=N+1、阻带截止频率ωs和选定的窗函数,采用Matlab工具箱函数fir1(\5)和freqz(\5)可确定FIR低通滤波器的单位冲激响应和幅频响应。
2.2 切比雪夫逼近法
切比雪夫逼近法也称为最佳一致逼近法,是着眼于在相关区间,使误差函数
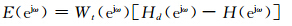
较为均匀一致,通过合理地选择H(ejω)和权函数Wt(ejω),使E(ejω)的值达到最小。利用切比雪夫逼近理论设计低通数字滤波器共需5个参数,即通带波纹峰值δp、阻带波纹峰值δs、通带截止频率ωp、阻带截止频率ωs、单位抽样响应长度M。权函数的取值取决于通带和阻带的逼近精度要求:

一般情况下,滤波器的设计指标以ωp、ωs、Ap、As 给出,Ap和As与δp和δs的换算关系参见文献[11]。依据逼近指标,采用firpmord(\5)函数可估算出滤波器的最低阶数、误差加权向量和归一化频率向量,从而使滤波器在满足指标的前提下造价最低。但在很多情况下,采用估算出的参数来设计的滤波器的滤波效果并不能完全令人满意,这时可通过增大滤波器的阶数来进行调节。从原理上看,相对于窗函数法,切比雪夫逼近法能在一致意义上对Hd(ejω)做最佳逼近,因而获得了较好的通带和阻带性能,并能准确地指定通带和阻带的边缘[11]。
3 数值计算与分析 3.1 滤波器参数设置
设飞机的飞行速度v=100 m/s,GPS数据采样间隔为Tc=1s,待设计滤波器能抑制波长小于2 km的分量,而让波长大于10 km的所有分量通过,则通带截止频率fp和阻带截止频率fs分别为:

因采样频率fc=1/Tc=1 Hz,对fp和fs进行归一化:
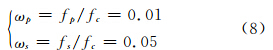
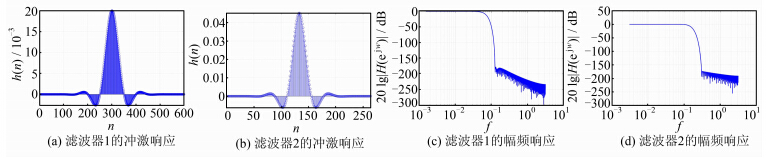
同时设置低通滤波器的通带最大衰减Ap=0.25 dB,阻带最小衰减为As=180 dB。在实际数据处理中,可采用两种方法来调节Ap和As这两个参数。在有地面检校值的测区,将地面观测值向上延拓至空中,并与航空重力观测值进行比较,当二者之差的RMS最小时,可确定Ap和As。在有GPS水准数据的测区,当由航空重力观测值解算的大地水准面高与GPS水准之差的RMS最小时,可确定Ap和As。为了便于陈述,将利用窗函数法和切比雪夫逼近法设计的FIR低通滤波器分别称为滤波器1和滤波器2。图 1分别给出了两种滤波器的单位冲激响应和幅频响应。
|
| 图 1 低通滤波器的冲激响应和幅频响应 Fig. 1 Impluse Response and Amplitude Response of Low-pass Filters |
为了验证滤波器的性能,本文采用了文献[7]中的模拟算例。算例的具体参数如下:飞机的平均飞行高度为1 500 m,飞行时有15 m的起伏,续航时间为4 800 s,低频高程剖面是周期为T0=300 s(ω0=2π/T0)的谐振荡,即
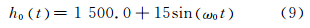
本文以h0(t)差分后得到的速度和加速度作为参考真值。高程扰动由5个高频信号叠加而成:
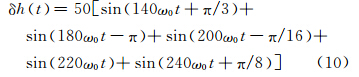
上述模型中,低频部分的波长为30 km,位于所设计的低通滤波器的通带;高频部分波长小于2 km,位于所设计的低通滤波器的阻带。采用式(1)分别对h0(t)及h1(t)=h0(t)+δh(t)作差分运算得到速度,由图 2(b)的计算结果不难发现,差分运算是一个噪声放大的过程。要从含有高频噪声的位置信号中得到准确的速度和加速度信息,必须对h1(t)的差分结果作低通滤波处理。
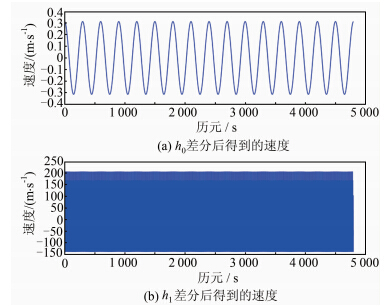
|
| 图 2 由h0和h1得到的速度 Fig. 2 Velocities from h0 and h1 |
采用所设计的两种低通滤波器对 h1(t)的差分结果做低通滤波处理,所得结果见图 3。通过对比发现,本文所设计的滤波器具有较强的滤波效果,但与速度真值相比,滤波后得到的速度除了在开始部分含有较大的幅度误差外,还存在明显的相位移动,这是因为FIR滤波器会引入相位延迟。设滤波器长度为M,则相位延迟为(M-1)/2。显然,只有滤波器长度为奇数时,相位延迟才是整数值。滤波器1和滤波器2的长度分别为601和265,其相位延迟分别为300和132。当信号长度较短时,一般采用端点延拓法[13]和向前向后滤波法[14]来消除相位延迟。考虑到航空重力 测量的作业时间长,数据量大,本文将端点处的相位延迟直接删除,即将滤波后的速度序列向前移动(M-1)/2个历元,使得滤波后的速度序列与参考速度序列的起始端点对齐,但滤波后的速度序列长度要比参考速度序列短 (M-1)/2个历元。
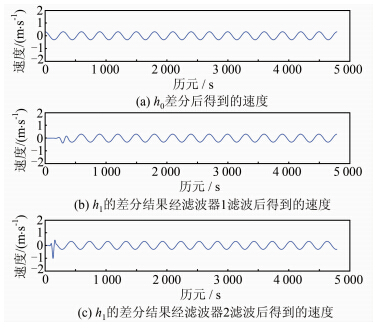
|
| 图 3 对含有噪声的速度滤波后的结果 Fig. 3 Filtered Results of the Noisy Velocities |
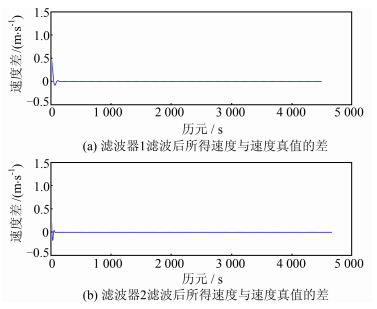
对图 3(b)和图 3(c)的速度进行相位延迟改正,并与速度参考值做差,所得结果见图 4。从图 4中可以看出,消除相位延迟后的滤波结果与参考值之差大部分接近于0,但在开始部分仍含有部分无效数据,这是因为滤波过程存在边界效应,还需要对数据进行截短,截短长度也与滤波器长度M有关,为(M-1)/2。与相位延迟改正一样,只有当M为奇数时,截短长度才是整数。对相位延迟改正后的速度序列截短,其起始端点比与参考速度序列的端点落后(M-1)/2个历元,同时相应的序列长度比参考序列短(M-1)个历元。
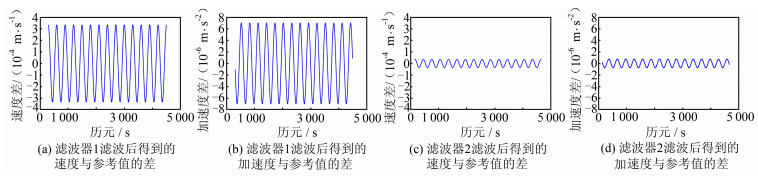
对截短后的速度序列再次差分,可得加速度序列。滤波后得到的速度序列、加速度序列与参考值之差见图 5和表 1。结果显示,采用滤波器1所得到的速度序列和加速度序列的精度分别为2.35×10-4 m/s、0.49 mGal,采用滤波器2所得到的速度序列和加速度序列的精度则分别为0.25×10-4 m/s、0.052 mGal,这说明本文所设计的低通滤波器可以将高频扰动分离出来,对滤波后的时间序列进行相位延迟改正和边界效应改正后,能从含有噪声的位置信息中提取出高精度的速度和加速度信息。同时也发现,当设计指标完全相同时,依照窗函数法所设计的 FIR低通滤波器的长度较长,因此,从计算机的角度看,其设计的滤波器造价更高;从数据处理的角度来看,滤波后进行相位延迟改正和数据截短时,损失的有效信息更多,表 1中的“比较点数”也验证了这一点。
|
| 图 4 相位延迟校正后所得速度与参考值的差 Fig. 4 Differences of Velocities with Reference Values After Phase-delay Eliminated |
| 滤波后所得速度序列与参考值之差 | 滤波后所得加速度序列与参考值之差 | |||||||||
| 比较点数/个 | 速度差/(10-4 m·s-1) | 比较点数/个 | 加速度差/(10-5 m·s-2) | |||||||
| 最小值 | 最大值 | 平均值 | 标准差 | 最小值 | 最大值 | 平均值 | 标准差 | |||
| 窗函数法 | 4 194 | -3.33 | 3.33 | -0.005 | 2.35 | 4 188 | -0.7 | 0.7 | 0.21 | 0.49 |
| 切比雪夫逼近法 | 4 530 | -0.35 | 0.35 | 0.000 2 | 0.25 | 4 524 | -0.08 | 0.08 | -0.032 | 0.052 |
|
| 图 5 信号截短后所得速度、加速度与参考值之差 Fig. 5 Differences of Velocities,Accelerations with Reference Values After Data Cutoff |
选取美国地区的2个IGS站的GPS观测数据,测站编号分别为A和B,基线长度为30 km,数据采样间隔为1 s,观测持续时间为2 h。设测站 A的坐标固定,将B的坐标观测值与
A的坐标相减,可得到三维时间序列(x → AB,y → AB,z → AB),采用式(1)对该时间序列作一次差分和二次差分后,可得测站B相对于测站A的速度矢量V → 0和加速度矢量a → 0。在短时间内,可认为测站B的相对速度和相对加速度均为零,
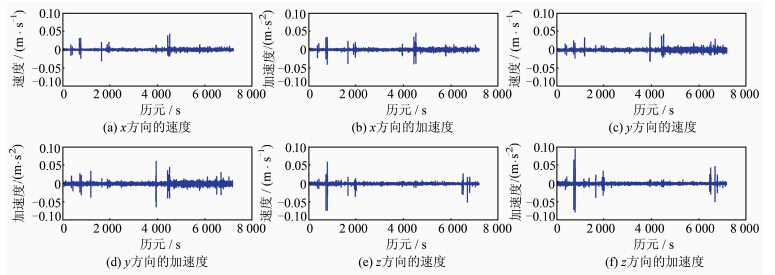
但图 6表明V → 0和a → 0中含有高频噪声,因此必须对差分结果做低通滤波处理。对静态GPS数据的低通滤波处理流程与模拟算例类似。本文通过试算发现,采用firpmord(\5)函数估算出的滤波器2的阶数N不能满足要求(滤波器长度M=N+1),本文在处理静态GPS数据时,将N的值增大至564。
|
| 图 6 滤波前测站B的速度V0和加速度a0 Fig. 6 Velocities V0 and Accelerations a0 of Station B Before Lowpass Filtering |
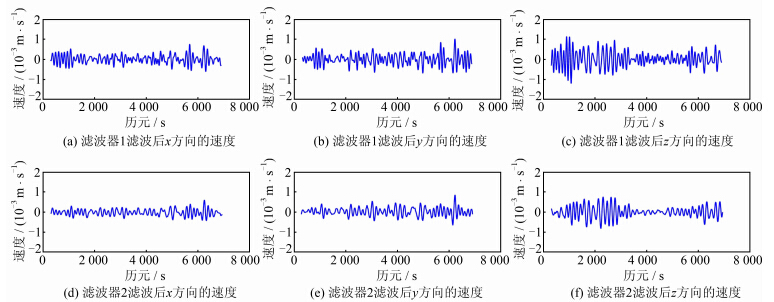
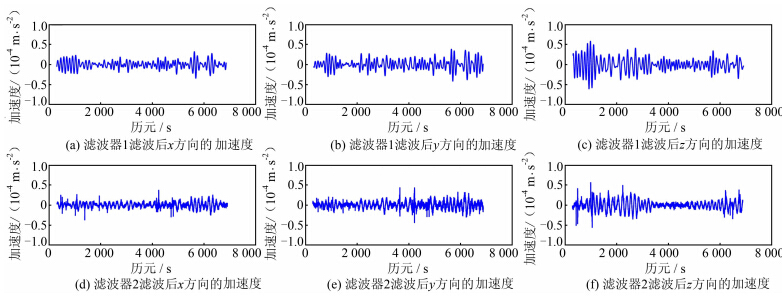
图 7和图 8描述了低通滤波后测站 B的x、y、z 三个方向的相对速度和相对加速度随时间的变化,表 2给出了相关统计信息。因测站B的相对速度和相对加速度的参考值均为零,滤波后所得速度和加速度的标准差即能反映滤波处理的精度。由表 2可知,滤波器2的滤波效果要稍好于滤波器1,采用滤波器2滤波后,测站B的垂直加速度能达到±(1~2) mGal的精度,这与文献[9]的结果相当,而水平加速度的精度在±1 mGal以内,这是因为GPS的定位精度在水平方向上较垂直方向上高。图 6中的速度和加速度在某些历元处误差较为显著,这是因为在相应历元处,测站B的相对位移存在较大变化,如图 9所示。滤波后得到的速度和加速度中对应的历元处并未出现显著的异常情况,说明本文设计的低通滤波器的性能良好,有效消除了高频噪声的影响。
| 低通滤波后所得速度的统计信息 | 低通滤波后所得加速度的统计信息 | |||||||||||
| 方向 | 比较点数/个 | 速度差/(10-4 m·s-1) | 方向 | 比较点数/个 | 加速度差/(10-5 m·s-2) | |||||||
| 最小值 | 最大值 | 平均值 | 标准差 | 最小值 | 最大值 | 平均值 | 标准差 | |||||
| 窗函 | x | 6 594 | -6.19 | 7.53 | -0.008 | ±2.09 | x | 6 588 | -3.45 | 3.36 | -0.004 | ±0.98 |
| 数法 | y | 6 594 | -6.89 | 10 | 0.048 | ±2.68 | y | 6 588 | -4.23 | 3.95 | -0.005 | ±1.27 |
| z | 6 594 | -12 | 11 | 0.062 | ±3.63 | z | 6 588 | -6.12 | 6.04 | 0.002 | ±1.71 | |
| 切比 | x | 6 630 | -4.14 | 6.17 | -0.005 | ±1.55 | x | 6 624 | -3.85 | 3.83 | -0.000 7 | ±0.66 |
| 雪夫 | y | 6 630 | -6.74 | 8.36 | 0.052 | ±1.99 | y | 6 624 | -4.54 | 4.46 | 0.000 2 | ±0.84 |
| 逼近法 | z | 6 630 | -8.23 | 7.60 | -0.037 | ±2.64 | z | 6 624 | -5.64 | 5.79 | -0.003 | ±1.12 |
|
| 图 7 滤波后测站B的速度 Fig. 7 Velocities of Station B After Lowpass Filtering |
|
| 图 8 滤波后测站B的加速度 Fig. 8 Accelerations of Station B After Lowpass Filtering |

|
| 图 9 测站B相对平面坐标的变化 Fig. 9 Variation of Relative Horizontal Positions of Station B |
在航空矢量重力测量数据处理中,由于高频噪声的存在以及差分过程对噪声的放大,对GNSS位置时间序列直接作差分往往得不到高精度的速度和加速度,这对获取高精度的重力矢量信息十分不利。本文采用窗函数法和切比雪夫逼近法设计了两类FIR低通滤波器,并对模拟的高程信号和实测的静态GPS数据进行了处理。结果表明,本文设计的滤波器具有较好的滤波效果,对静态GPS测量数据低通滤波后,能以±(1~2) mGal的精度确定垂直加速度,以优于±1 mGal的精度确定水平加速度。此外,在相同的设计指标下,依照切比雪夫逼近法设计的滤波器长度更短,滤波效果更佳,在处理实测的航空重力矢量数据时,建议采用切比雪夫逼近法来设计FIR滤波器。值得注意的是,本文的结果是基于GPS静态定位数据得到的,在实际的航空重力矢量测量中,对动态数据的滤波效果还需更进一步的研究。
| [1] | Bruton A M. Improving the Accuracy and Resolution of SINS/DGPS Airborne Gravimetry[D].Calgary:University of Calgary, 2000 |
| [2] | Sun Zhongmiao. Theory, Mothods and Applications of Airborne Gravimetry[D]. Zhengzhou:Information Engineering University, 2004(孙中苗. 航空重力测量理论、方法及应用研究[D]. 郑州:信息工程大学, 2004) |
| [3] | Jekeli C, Garcia R. GPS Phase Accelerations for Moving Base Vector Gravimetry[J]. Journal of Geodesy, 1997, 71:630-639 |
| [4] | Hwang C, Hsiao Y S, Shih H C. Data Reduction in Scalar Airborne Gravimetry:Theory, Software and Case Study in Taiwan, China[J]. Computers & Geosciences, 2006, 32(10):1 573-1 584 |
| [5] | Childers V A, Bell R E, Brozena J M. Airborne Gravimetry:An Investigation of Filtering[J]. Geophysics, 1999, 64(1):61-69 |
| [6] | Guo Zhihong,Luo Feng,Wang Ming,et a1.The Design and Experiment of ⅡR Lowpass Digital Filters for Airborne Gravity Data[J].Chinese J Geophys,2011,54(8):2 148-2 153 (郭志宏, 罗锋, 王明, 等. 航空重力数据无限脉冲响应低通数字滤波器设计与试验研究[J]. 地球物理学报, 2011, 54(8):2 148-2 153) |
| [7] | Sun Zhongmiao, Xia Zheren. Design of FIR Lowpass Differentiator and Its Application in Airborne Gravimetry[J]. Chinese J Geophys, 2000, 43(6):850-855(孙中苗, 夏哲仁. FIR低通差分器的设计及其在航空重力测量中的应用[J]. 地球物理学报, 2000, 43(6):850-855) |
| [8] | Xu Tianhe. Recoverying the Gravitational Potential Model from the Ephemerides and Accelermeter of CHAMP[D].Zhengzhou:Information Engineering University, 2004(徐天河. 利用CHAMP卫星轨道和加速度计数据推求地球重力场模型[D]. 郑州:信息工程大学, 2004) |
| [9] | Zhong Bo. Study on the Determination of the Earth's Gravity Field from Satellite Gravimetry Mission GOCE[D]. Wuhan:Wuhan University, 2010(钟波. 基于GOCE卫星重力测量技术确定地球重力场的研究[D]. 武汉:武汉大学, 2010) |
| [10] | Wang Qianxin, Xu Tianhe, Gong Youxing. Optimal Points of Using Central Differences Method for GPS Velocity Determination[J]. Geomatics and Information Science of Wuhan University, 2012, 37(3):265-268(王潜心, 徐天河, 龚佑兴. 利用中心差分法进行 GPS 定速时最佳点数的选取[J]. 武汉大学学报·信息科学版, 2012, 37(3):265-268) |
| [11] | Gao Xiquan, Ding Yumei, Kuo Yonghong, et al. Theory, Implementation and Application of Digital Signal Processing[M]. Beijing:Electronic Industry Press,2010 (高西全,丁玉美,阔永红,等. 数字信号处理——原理、实现及应用[M]. 北京:电子工业出版社, 2010) |
| [12] | Hu Guangshu. Theory, Algorithm and Implementation of Digital Signal Processing[M]. Beijing:Tsinghua University Press,2012 (胡广书. 数字信号处理——原理、算法与实现[M]. 北京:清华大学出版社, 2012) |
| [13] | Fu Yanjun, Cheng Qiangqiang, Yu Runqiao, et al. Eleminate Phase Delay of FIR Filtered Signal[J]. Computer Engineering and Applications,2012,48(7):146-149 (伏燕军,程强强,于润桥,等. 信号FIR数字滤波后相位延迟的消除[J]. 计算机工程与应用, 2012, 48(7):146-149) |
| [14] | Wan Xiaoyun, Yu Jinhai, Zeng Yanyan. Frequency Analysis and Filtering Processing of Gravity Gradients Data from GOCE[J]. Chinese J Geophys, 2012, 55(9):2 909-2 916(万晓云,于锦海,曾艳艳. GOCE引力梯度的频谱分析及滤波[J]. 地球物理学报, 2012, 55(9):2 909-2 916) |
 2015, Vol. 40
2015, Vol. 40


