文章信息
- 柯灝, 李斐, 赵建虎, 王泽民
- KE Hao, LI Fei, ZHAO Jianhu, WANG Zemin
- 利用潮汐性质相似性的长江口水域深度基准面传递精度研究
- A Chart Datum Transfer Precision Model in the Yangtze River Estuary Based on Tidal Nature Similarity
- 武汉大学学报·信息科学版, 2015, 40(6): 767-771
- Geomatics and Information Science of Wuhan University, 2015, 40(6): 767-771
- http://dx.doi.org/10.13203/j.whugis20130055
-
文章历史
- 收稿日期:2013-04-18
2. 武汉大学测绘学院, 湖北 武汉 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
海洋深度基准面的精确确定是水下地形测量成果向海图深度精确转换的一个关键环节,深度基准面传递方法在解决短期或临时验潮站水域的深度基准面确定问题时发挥着重要作用,因此,传递精度是需要关注的一个重要指标[1, 2]。
深度基准面的传递精度一般受传递距离、同步时长、地形环境等因素的影响[2]。目前对深度基准面传递的外在限制条件如最小同步观测时长、最大传递距离、适合传递的地形条件等也有所研究,并给出了相关的限定参数或条件,然而对这些外在因素的影响却没有作定量的估计。实际上,当传递距离过大或地形环境特征复杂时,传递精度较差的根本原因是由于潮汐性质发生改变、潮汐传播非线性等造成[3]。为此,本文提出以潮汐类型差、传递距离、地形环境特征作为深度基准面传递的参考指标,结合长江口区域若干长期验潮站的潮位观测资料展开试验,研究深度基准面传递精度模型,同时为其他水域的深度基准面传递精度模型的构建提供参考。
1 深度基准面传递精度影响因素 1.1 潮汐类型差
深度基准面传递的前提是基于潮汐性质相似,而潮汐性质可根据一天之内高潮和低潮的次数简单地概括为半日潮、全日潮和混合潮,该方法只能定性地判定潮汐的类型。目前可依据潮汐调和常数来精确定量地计算潮汐的类型值。我国潮汐类型的判断标准如下[4, 5, 6]:
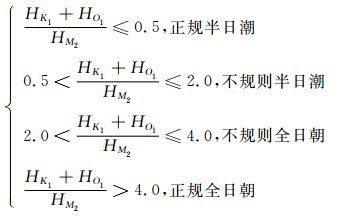
根据K1、O1、M2三个分潮各自振幅之间的关系不仅可定性判断潮汐类型,而且能在量级上精确地分析潮汐性质间的相关度。若以T表示潮位站潮汐类型值,并假定某一阈值t,当不同两地潮汐类型值之间的差值 ΔT ≤t时,认为潮汐性质接近,具备了深度基准面传递的必要条件,因此潮汐类型值差可作为深度基准面传递的一个重要指标。
1.2 传递距离
《海道测量规范》[7]里并未对深度基准面的传递距离作出明确规定,在实际外业中,考虑到传递距离对传递精度的影响,一般采用就近原则选取最短的传递距离进行传递。然而实质上若距离相隔很远,但潮汐性质仍然相似,则传递精度也理应较高。因此,在保证传递精度的前提下,研究深度基准面可传递的最大距离对减小临时验潮站的布设密度,缩减成本开支具有重要意义。
1.3 地形环境特征
地形环境特征对传递精度的影响不可忽视。在平坦开阔水域,潮汐传播多以前进波为主,更易满足潮汐性质基本相同、潮波线性传播的条件,因此传递精度较高;而在地形变化复杂或走向蜿蜒曲折的岸线,由于潮波传播多以驻波为主,不易满足上述条件,因此传递精度较低[2]。由于长江口北支流域蜿蜒狭长,水岸线变化曲折复杂,因此在该区域深度基准面传递精度分析中,对地形环境造成的影响需着重考虑。
2 长江口水域传递精度模型确定
为验证本文所述思想的正确性以及确定具体的深度基准面传递精度模型,以位于长江口区域的营船港、徐六泾、白茆、杨林、崇头、六 、共青圩、青龙港、灵甸港和连兴港共计10个长期验潮站为例(如图 1所示),分别根据各自2007年潮位观测资料进行潮汐调和分析,得到各站K1、O1、M2三个分潮的振幅,继而计算可得各验潮站的潮汐类型值,结果如图 2所示。

|
| 图 1 长江口验潮站分布示意图 Fig. 1 Tidal Gauges Distribution in the Yangtze River Estuary |
|
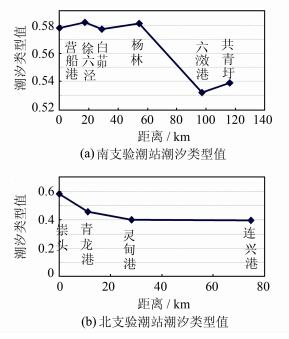
| 图 2 南北两支验潮站潮汐类型变化图 Fig. 2 Change Trend of Tidal Types in the North and South Branches |
从图 2中各站的潮汐类型值来看,南支前四站营船港至杨林四个站以及北支入口处的第一个验潮站崇头之间的潮汐类型值非常接近,之间的互差基本都在0.01以内;南支末端两站六 和共青圩的互差也在0.01以内,但与南支前四站的潮汐类型值差值较大,差值基本在0.05左右。北支前三站从崇头至灵甸港三站之间的互差较大,北支末端两站则十分接近,差值在0.01以内。
从图 2中可看到,南支前四个验潮站之间的距离分布较均匀,从营船港到杨林相距接近60 km,杨林到六 站的距离则在40 km左右,而六 到共青圩之间的距离在20 km左右。北支前三站之间较近,均在20 km以内,第四个验潮站则分布较远,与第三站间的距离接近50 km。为研究深度基准面传递精度与潮汐类型值、传递距离间的量化关系,以这10个验潮站为研究对象,研究在不同传递距离和不同同步观测时间下深度基准面的传递精度。
从南支的起始站营船港开始,到共青圩结束共六站,依次从第一个验潮站逐一向后一个验潮站进行传递,共15组传递试验。传递的同步时长分别为3 d、7 d、15 d、30 d,传递方法为最小二乘潮位拟合综合传递法。15组传递试验结果如表 1所示
| 区间 | 距离/km | 潮汐类型差绝对值/cm | 3 d/cm | 7 d/cm | 15 d/cm | 30 d/cm | 最大绝对误差/cm | 绝对误差均值/cm | 中误差/cm | |
| 营船港-徐六泾 | 17.4 | 0.004 | -2.5 | -1.0 | -0.3 | -5.1 | 5.1 | 2.2 | 3.3 | |
| 营船港-白茆 | 29 | 0.001 | -2.7 | -2.8 | -3.2 | -5.2 | 5.2 | 3.5 | 4.2 | |
| 营船港-杨林 | 55 | 0.003 | 1.4 | -2.9 | -3.6 | -1.4 | 3.6 | 2.3 | 2.9 | |
| 营船港-六 | 97 | 0.046 | -17.9 | -23.3 | -21.9 | -24.1 | 24.1 | 21.8 | 25.3 | |
| 营船港-共青圩 | 115.9 | 0.039 | -39.0 | -43.6 | -38.9 | -38.2 | 43.6 | 39.9 | 46.2 | |
| 徐六泾-白茆 | 11.6 | 0.005 | 7.2 | 5.9 | 5.0 | 2.7 | 7.2 | 5.2 | 6.3 | |
| 徐六泾-杨林 | 37.6 | 0.001 | -1.1 | -1.5 | -2.6 | 5.4 | 5.4 | 2.7 | 3.6 | |
| 徐六泾-六 | 79.6 | 0.050 | 4.5 | -0.3 | -0.8 | 3.6 | 4.5 | 2.3 | 3.4 | |
| 徐六泾-共青圩 | 98.5 | 0.043 | -27.6 | -27.2 | -28.8 | -18.8 | 28.8 | 25.6 | 29.9 | |
| 白茆-杨林 | 26 | 0.003 | 2.2 | 1.9 | -0.8 | 2.3 | 2.3 | 1.8 | 2.2 | |
| 白茆-六 | 68 | 0.045 | 3.9 | 1.6 | 2.2 | 1.4 | 3.9 | 2.3 | 2.9 | |
| 白茆-共青圩 | 86.9 | 0.038 | -11.8 | -21.2 | -10.0 | -19.7 | 21.2 | 15.7 | 18.9 | |
| 杨林-六 | 42 | 0.049 | -0.2 | -0.9 | -0.8 | -2.5 | 2.5 | 1.1 | 1.6 | |
| 杨林-共青圩 | 60.9 | 0.042 | -0.5 | 2.8 | 7.4 | 1.0 | 7.4 | 2.9 | 4.6 | |
| 六俲-共青圩 | 18.9 | 0.007 | -10.2 | -4.2 | -3.8 | -4.7 | 10.2 | 5.7 | 7.3 |
表 1中,潮汐类型数差值均在0.05以内,最大传递距离为115.9 km时,传递中误差为46.2 cm。当传递距离在80 km以内时,传递中误差基本都在8 cm以内,传递精度较高。继续选取南支若干潮位站进行试验。由于崇头站地处南北两支分岔口位置,且潮汐类型值与南支各站比较接近,因此以崇头为基准,其余南支各站与崇头间进行深度基准面传递,传递结果如表 2所示。
| 区间 | 距离/km | 潮汐类型差绝对值/cm | 3 d/cm | 7 d/cm | 15 d/cm | 30 d/cm | 最大绝对误差/cm | 绝对误差均值/cm | 中误差/cm |
| 营船港-崇头 | 38.1 | 0.005 | 2.8 | -0.5 | 4.6 | 1.3 | 4.6 | 2.3 | 3.2 |
| 徐六泾-崇头 | 20.7 | 0.001 | 3.3 | 1.2 | 0.2 | 2.7 | 3.3 | 1.9 | 2.6 |
| 白茆-崇头 | 11 | 0.006 | 7.8 | 5.4 | 3.0 | 0.6 | 7.8 | 4.2 | 5.8 |
| 崇头-杨林 | 24.3 | 0.002 | 0.6 | 0.8 | 1.6 | 2.4 | 2.4 | 1.4 | 1.8 |
| 崇头-六 | 60.5 | 0.051 | 4.8 | 4.7 | 1.5 | 0.7 | 4.8 | 2.9 | 4.0 |
| 崇头-共青圩 | 79 | 0.044 | 1.4 | 2.0 | 2.4 | -3.3 | 3.3 | 2.3 | 2.7 |
在表 2中,共进行了6组传递试验,潮汐类型数差值最大为0.051,最大传递距离为崇头到共青圩79 km,传递中误差都在6 cm以内,传递精度较稳定。
综合表 1、表 2的试验结果,由于站间潮汐类型值差异基本都在0.05以内,将传递中误差按照距离大小依次展开绘制,如图 3所示。
|
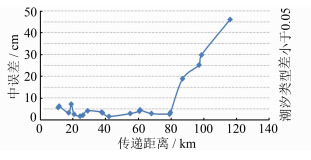
| 图 3 南支区域不同距离下深度基准面传递精度 Fig. 3 Chart Datum Transfer Precisions Under the Different Distances in the Sorth Branch |
从图 3中可以直观地看到传递精度误差曲线在80 km处出现较大的变化,当传递距离小于 80 km时,传递中误差优于8 cm;而当传递距离 大于80 km时,传递误差近似呈线性递增趋势,增幅大概在1 cm/km左右。上述试验结果说明,在长江口南支区域,潮汐性质接近,在保证传递精度的前提下,深度基准面的最大传递距离可达到80 km左右,若传递距离超过80 km,则精度较差,不可传递。
上述试验是对长江口南支深度基准面传递精度模型的研究,下面以北支流域为研究区域,从崇头开始,依次向北支其余验潮站进行深度基准面传递。由于青龙港同灵甸港没有同期观测数据,因此在传递试验中以青龙港直接向连兴港传递。传递结果如表 3所示。
| 区间 | 距离/km | 潮汐类型差绝对值/cm | 3 d/cm | 7 d/cm | 15 d/cm | 30 d/cm | 最大绝对误差/cm | 绝对误差均值/cm | 中误差/cm |
| 崇头-青龙港 | 11.2 | 0.126 | 17.0 | 19.1 | 18.3 | 15.5 | 19.1 | 0.175 | 20.2 |
| 崇头-灵甸港 | 28.2 | 0.181 | 28.6 | 20.4 | 22.0 | 19.5 | 28.6 | 0.226 | 26.4 |
| 崇头-连兴港 | 74.8 | 0.185 | 75.3 | 74.7 | 65.2 | 60.7 | 75.3 | 0.690 | 79.9 |
| 青龙港-连兴港 | 63.6 | 0.059 | -44.3 | -35.9 | -48.0 | -41.4 | 48.0 | 0.424 | 49.2 |
| 灵甸港-连兴港 | 46.6 | 0.004 | -16.0 | -10.7 | -19.0 | -18.7 | 19.0 | 0.161 | 18.9 |
从表 3可知,北支区域验潮站间的潮汐类型值差异较大,前四组站间的差值都在0.05以上,其中最大差值为崇头和连兴港之间,为0.185。四组传递结果精度都较差,即使崇头和青龙港之间的距离只有11.2 km,但传递中误差却达到了20.2 cm。最后一组灵甸港向连兴港的传递试验,尽管站间潮汐类型差值很小,为0.004,传递距离为46.6 km,但传递精度较差,传递中误差为18.9 cm。将表 3中北支区域的传递结果按距离大小依次绘图,如图 4所示。
|
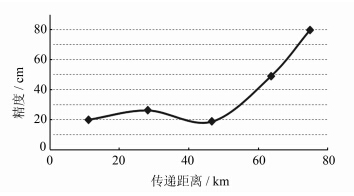
| 图 4 北支区域不同距离下深度基准面传递精度 Fig. 4 Chart Datum Transfer Precisions Under the Different Distances in the North Branch |
将该组试验结果同长江口南支区域的试验结果相比,在北支区域,潮汐类型值差普遍大于0.1,潮汐性质也从北支起始端的混合潮逐渐过渡为半日潮,因此在北支区域的前几组传递试验中,即使传递距离不大,但传递精度却较低。而在北支区域最后两验潮站间,尽管潮汐类型值差为0.004,潮汐性质十分接近,传递距离也小于80 km,但传递精度依然较低,由此验证了§1.3中关于地形环境特征对深度基准面传递精度影响的思想。
在图 1中,长江口北支水域狭长且蜿蜒曲折,潮波在传播过程中波长和频率均会发生不规则的改变,潮波多以驻波占优,而最小二乘潮位拟合综合传递法的前提则是基于潮波均匀传播,因此在北支水域,即使传递距离较小,但深度基准面的传递精度依然较低。
图 5为长江口南北区域验潮站深度基准面和平均海平面的变化情况。图 5(b)中,长江口南支验潮站深度基准面的变化趋势较平缓,近似呈一条平行于横轴的直线。北支各验潮站间深度基准面之间的差异较大,且为非线性变化。这进一步验证了北支区域由于地形狭长,水岸线曲折,传递的地形环境较差,导致北支区域深度基准面传递精度较低的结论。

|
| 图 5 北支/南支深度基准面和长期平均海平面变化趋势 Fig. 5 Change Trend of Chart Datum and Mean Sea Level in North and South Branches |
综上所述,根据本文试验结果,可得长江口南北两支水域深度基准面的传递精度模型如下:
1) 在长江口南支区域,潮汐类型值差值均小于0.05,潮汐性质接近,可进行深度基准面传递。最大传递距离为80 km,传递精度一般优于8 cm,当传递距离大于80 km时,深度基准面传递精度逐渐下降,下降速率大概为1 cm/km左右。
2) 在长江口北支区域,潮汐类型值差异较大,地形特征较狭长复杂,水岸线变化曲折,传递精度一般。当传递距离小于40 km时,深度基准面传递精度一般在20 cm左右,当传递距离大于40 km时,精度迅速下降,传递误差近似以3 cm/km的速率递增。
3 结 语
本文针对深度基准面传递精度问题,提出以潮汐类型值差、传递距离、地形环境特征为参考指标,给出了长江口区域南北两支深度基准面传递精度模型,对该区域深度基准面传递精度指标估计及其他水域深度基准面传递精度模型的构建提供了参考。
| [1] | Zhao Jianhu, Zhang Hongmei, Clarke J E H. Establishment of Local Seamless Vertical Datum[J]. Geomatics and Information Science of Wuhan University,2006,31(5):448-450(赵建虎,张红梅,Clarke J E H.局部无缝垂直参考基准面的建立方法研究[J].武汉大学学报·信息科学版,2006,31(5):448-450) |
| [2] | Sun Xinxuan, Liu Yanchun, Bao Jingyang, et al. Study on Precision of Chart Datum Transfer Algorithm[J]. Journal of Geomatics Science and Technology,2009,26(3):228-231(孙新轩,刘雁春,暴景阳,等.海图深度基准面传递算法的精度分析[J].测绘科学技术学报,2009,26(3):228-231) |
| [3] | Bao Jingyang, Huang Chenhu, Liu Yanchun,et al. Research on the Algorithm for Chart Datum[J]. Hydrographic Surveying and Charting,2003,23(1):8-12(暴景阳,黄辰虎,刘雁春,等.海图深度基准面的算法研究[J].海洋测绘,2003,23(1):8-12) |
| [4] | Liu Yanchun. Space Structure and Data Processing in Marine Sounding[M]. Beijing:Surveying and Mapping Press,2003(刘雁春.海洋测深空间结构及其数据处理[M].北京:测绘出版社,2003) |
| [5] | Huang Zuke, Huang Lei. Tidal Theory and Calculation[M].Qingdao:China Ocean University Press,2005(黄祖珂,黄磊.潮汐原理与计算[M].青岛:中国海洋大学出版社,2005) |
| [6] | Huang Chenhu, Ma Fucheng, Lv Liang, et al. Application of Two Indexs in Judging Comparability About Tide Kind[J]. Hydrographic Surveying and Charting, 2007,27(6):12-15(黄辰虎,马福诚,吕良,等.潮汐性质相似性判断的两个指标及其应用[J].海洋测绘,2007,27(6):12-15) |
| [7] | The State Bureau of Quality and Technical Supervision. GB12327-1998, Specifications for Hydrographic Survey[S]. Beijing:Standards Press of China,1999(国家质量技术监督局.GB12327-1998 海道测量规范[S]. 北京:中国标准出版社,1999) |
 2015, Vol. 40
2015, Vol. 40


