文章信息
- 赵建虎, 董江, 柯灝, 张红梅
- ZHAO Jianhu, DONG Jiang, KE Hao, ZHANG Hongmei
- 远距离高精度GPS潮汐观测及垂直基准转换研究
- High Precision GPS Tide Measurement Method in a Far-Distance and Transformation Model for the Vertical Datum
- 武汉大学学报·信息科学版, 2015, 40(6): 761-766
- Geomatics and Information Science of Wuhan University, 2015, 40(6): 761-766
- http://dx.doi.org/10.13203/j.whugis20130314
-
文章历史
- 收稿日期:2013-07-09
2. 武汉大学中国南极测绘研究中心, 湖北 武汉 430079;
3. 武汉大学动力与机械学院, 湖北 武汉 430072
2. Chinese Antarctic Center of Surveying and Mapping, Wuhan University, Wuhan 430079, China;
3. School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China
近年来,国内外一些大地测量学家借助GPS RTK(real time kinematic)技术在近岸(小于20 km)开展了船基/浮标GPS在航潮位测量,并取得了一定的效果[1]。但要在外航道、锚地等远岸水域实施潮位测量,仍面临着如下问题:①远距离、高精度GPS潮位测量技术及提取技术;②如何将GPS潮位转换为基于当地平均海平面或深度基准面潮位。对于第一个问题,在离岸较近或内航道水域,风浪较小,GPS验潮载体姿态的变化对高程影响较小,然而在离岸较远的海域,风浪引起载体姿态在空间上的变化将给验潮带来较大误差[2, 3, 4, 5]。Alkan 通过试验测定由测船横摇和纵摇引起的误差可达5 cm[2]。此外,GPS RTK模式还受距离限制,当距离超过15 km时,基本无法继续采用该模式。对于第二个问题,在近海岸,由于潮位站分布相对较多,借助潮位、水准点正常高和大地高数据,结合验潮站分布,可实现验潮站包围水域垂直基准关系的构建,垂直基准转换问题相对容易解决[6, 7];而在远岸,由于潮位站匮乏,上述垂直基准确定及转换方法很难适用。为此,本文将重点开展基于远距离GPS事后动态处理技术(post processing kinetic,PPK)的潮位测量及提取方法、垂直基准确定及转换模型构建两个问题的研究,以期实现远岸GPS潮位的精确测量及工程化应用。
1 远距离GPS潮位测量及提取
远距离GPS潮位测量系统主要由GPS和IMU(initial motion unit)组成[3, 4, 5]。通过基准站和流动站间的GPS数据开展PPK解算,获得流动站GPS天线处的瞬时三维解(X,Y,Z)PPK。若设定测量船/浮球重心在水面的投影点为船体坐标系原点,理想状态下GPS天线在船体坐标系下的坐标为(0,0,z),瞬时横摇和纵摇分别为r和p,则GPS天线在水面投影点的三维坐标(X,Y,Z)S为:

式中,R (A)、R(p)和 R (r)分别为方位A和姿态p、r构建的3×3旋转变换矩阵。
水面高程序列ZS是潮位T、波浪w、船体操纵dho等因素在垂直方向综合作用的结果,即

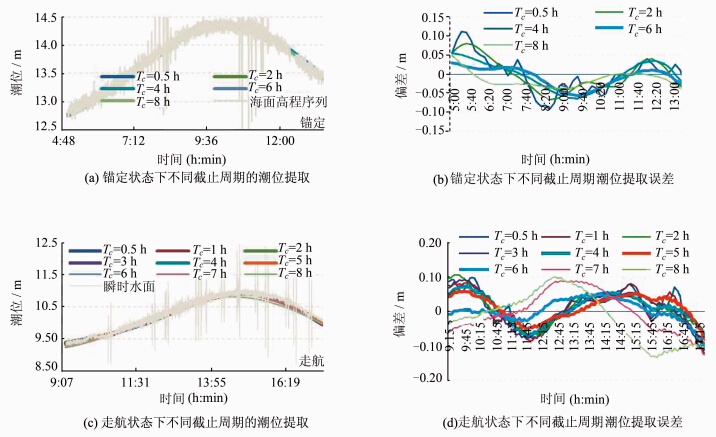
在诸要素中,潮位变化周期至少大于1 h,而其他要素的变化周期最大为几秒至十几分钟,T与ΔT存在着明显的周期差异,据此可设计基于FFT/Butterworth等低通滤波器实现潮位提取。潮位提取的一个关键问题是如何给定截止频率Fc/ 截止周期Tc。恰当的Tc应根据当地的潮汐周期特征以及测量状态(走航/锚定)来决定。图 1给出了一个正规半日潮水域PPK锚定和走航状态下,不同截止周期提取的潮位和与潮位站潮位比较所得的误差曲线。从图 1(b)可以看出,锚定状态下,当Tc=6 h时,潮位提取误差最小;在图 1(d)中,走航状态下,当Tc=4 h、5 h和6 h时,潮位提取误差都较小,均取得了较好的潮位提取效果,但当Tc>6 h时,潮位曲线均存在拉平现象,而当Tc<4 h时,则出现随潮位曲线波动的现象。相对锚定状态,走航PPK潮位的获取不但受整体潮位周期变化的影响,还受局部潮位特征变化的影响,截止周期相对锚定状态要小。因此,锚定状态下,Tc取当地潮位周期的1/2即可实现潮位的正确提取;而在走航状态下,取当地潮位周期的1/3~1/2。
|
| 图 1 锚定、走航状态下不同截止周期下提取的潮位曲线及误差曲线 Fig. 1 Tidal Levels and Errors Derived from Different Cut-off Periods at Anchored and On-the-Fly PPK Tidal Measurement |
基于以上方法获得了基于WGS84椭球的大地高潮位,而非基于当地平均海平面或深度基准面的实用潮位,下面研究垂直基准的确定及转换问题。
2.1 垂直基准面间及其相互关系的确定 2.1.1 同站潮位比较法
同一潮位站若具备不同基面(零点/平均海平面/深度基准面/WGS84椭球面)下的潮位观测值TB1和TB2,则直接比较两两潮位序列即可确定两基面间的关系。

式中,n代表潮汐观测个数;ΔB1-B2代表两个不同基准面间的偏差。
2.1.2 不同潮位站同基面综合传递法[7, 8]若长期站A潮位序列为TA(t),短期站B潮位序列为TB(t),两站为同基面(零点/平均海平面/深度基准面/WGS84椭球面)下的同步潮位,则二者的关系可描述为:

式中,x、y和z分别为两站潮差比、潮时差和基面偏差。则B站的平均海平面MSLB和深度基准面LB为:
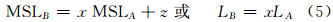
根据式(4)中各参数的物理意义及图 2所示的WGS84椭球面、深度基准面和平均海平面MSL间的关系,围绕GPS潮位测量,给出如下几种情况下的基面及其大地高确定方法。

|
| 图 2 垂直基准面间的关系 Fig. 2 Relation Among Vertical Datum |
1) 根据A站大地高的潮位和B站验潮站原始观测潮位,确定MSLB84和LB84。
A、B站存在同步潮位,若MSLA84/LA84已知,则借助式(6)可将A站基于平均海平面/深度基准面的潮位转换为基于大地高的潮位TA84。若A站为GPS潮位,则直接获得TA84:

基于式(4),可得z。z反映了A站基面(WGS84面)与B站基面(平均海平面/深度基准面)的差异,也即为B站的MSLB84/LB84:

2) 根据A、B潮位站潮位,确定MSLB84和LB84。
A、B站存在基于各自平均海平面/深度基准面的同步潮位站潮位,基于综合传递法,可得两站基面偏差z。若已知A站的MSLA84/LA84,并认为WGS84椭球面的曲率影响较小,可近似地认为是一平面,则有:

以上获得了每个验潮站的长期平均海平面MSL、深度基准面L及对应的MSL84和L84,也即为基于WGS84椭球面实测的PPK潮位向基于MSL/LMSL潮位的转换量。据此结合各潮位站的平面位置(x,y)p以及上述确定的各验潮站的转化量,构建测量水域无缝垂直基准转换模型f(x,y)。考虑WGS84椭球面为几何面,小区域范围内,两基面间的分离量MSL84/L84的变化仍主要取决于MSL/L的变化,为此,f(x,y)的构建采用距离加权平均方法。
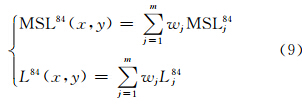
式中,wj为第j个潮位站上MSL84/L84的权,可根据距离给出。
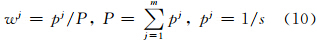
其中,s为第j个潮位站到内插位置(x,y)的距离。自此构建了区域无缝垂直基准间的转换模型,据此实现测量水域任意位置(x,y)的GPS潮位向基于当地平均海平面或深度基准面的潮位转换。
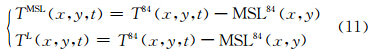
为检验本文所述方法的正确性,结合某工程开展了试验验证。测量水域有A、B和C三个验潮站,其中,A、B为岸边长期验潮站,C为海中临时验潮站,A-B、A-C和B-C间的距离分别为36 km、67 km和86 km,三站潮位均基于深度基准面;在B、C分别开展了64 h和23 h锚定PPK潮位测量,获得了基于WGS84大地高潮位。
3.1 基准关系构建
根据两类潮位站的观测数据,借助式(3)~式(8)推求了各潮位站深度基准面L及其L84。在B站,利用64 h的同步潮位站潮位和PPK锚定潮位,基于不同基面的综合传递法和潮位曲线比较法,分别计算出B站的L和L84如表 1所示。从表 1中可以看出,两种方法所得锚定位置的L、L84非常接近,互差小于1.5 cm。由于锚定位置与B潮位站非常接近,以B潮位站已知LB为参考,计算LB与综合传递法所求L以及LB与比较法所求L间的差值,其中最大偏差小于1.5 cm。最终确定LB=1.460 m,LB84=(12.356+12.363)/2=12.357 m。
| 潮位序列(类别) 潮位序列(类别) | 方法 | L84 /m | L /m | 已知L/m | dL /cm |
| B(潮位站潮位)B (PPK潮位) | 不同基面综合传递法 | 12.356 | 1.474 | 1.460 | 1.4 |
| B(潮位站潮位) B (PPK潮位) | 比较法 | 12.363 | 1.460 | 1.460 | 0.0 |
| B(大地高潮位) A(潮位站潮位) | 不同基面综合传递法1 | 12.380 | 1.267 | 1.280 | -1.3 |
| B(潮位站潮位) A(潮位站潮位) | 不同基面综合传递法2 | 12.433 | 1.267 | 1.280 | -1.3 |
对于A站,首先根据同步的B和A潮位站潮位,借助不同基面下的综合传递法,可得到B站深度基准面相对A站深度基准面的差z以及A站LA,由于B站LB84已知,则根据式(8)得到LA84。根据同步的B站PPK潮位与A站已知潮位,借助不同基面下的综合传递法,即式(7),获得A站的L和两基面差z,z也即为LA84。两种方法获得的A站L和LA84如表 1所示,二者所得L与实际偏差为-1.4 cm,LA84互差小于5 cm,取均值得LA84=12.406 m。
获得了A、B站的L和L84后,采用三种方法确定C站的L和L84。方法1:根据A、B站与C站38h同步潮位站潮位,借助综合传递法获得C站L以及两站深度基准面差z,借助式(8)实现C站L84的确定。方法2:比较C站的潮位站潮位和PPK潮位,直接确定C站的L84。方法3:利用A、B潮位站潮位和C站PPK潮位,基于式(7)确定L和L84。三种方法确定的C站LC和LC84如表 2所示。
| 方法 | 已知站/潮位类型 | 确定方法/同步时间 | C站潮位类型 | 站间距/km | PPK基线长度/km | (L/L84)/m | 最终(L/L84)/m | (ΔL/ΔL84)/cm |
| 1 | A潮位 | 不同基面综合 | 潮位 | 60 | 无 | 1.190/12.076 | 1.4/-1.2 | |
| B潮位 | 传递法2 / 38 h | 潮位 | 82 | 无 | 1.159/12.097 | -1.7/0.9 | ||
| 2 | C潮位 | 比较法/ 23 h | PPK | 0 | 60 | 1.176/12.115 | 0.0/2.7 | |
| 潮位 | 0 | 98 | 1.176/12.044 | 1.176/12.088 | 0.0/-4.4 | |||
| 3 | A潮位B潮位 | 不同基面综合传递法1/ 23 h | PPK | 60 | 60 | 1.190/12.052 | 1.4/3.6 | |
| 潮位 | 98 | 1.165/12.063 | -1.1/-2.5 | |||||
| PPK | 82 | 60 | 1.148/12.152 | -2.8/6.4 | ||||
| 潮位 | 98 | 1.239/12.028 | 6.3/-6.0 |
从表 2中可以得出以下结论。
1)各方法的传递精度ΔL和ΔL84均优于7 cm,达到了较好的一致。
2)同步观测时间较长的深度基准面L、L84的传递精度要高于同步观测时间较短的传递精度。此外,站间距离对传递精度也有一定的影响。距离越近,潮位特征的相关性越强,传递精度越高,PPK基线长度影响着PPK潮位精度,进而影响着L和L84的传递精度,因此距离越远,PPK定位精度和基准传递精度降低,但在100 km范围内,仍取得了优于6.5 cm的传递精度。
3) PPK潮位和潮位站潮位直接比较,可以高精度地获取该站两个潮位基面之间的差值,也即实现了高精度L84的确定。
3.2 潮位测量及其精度分析
获得各站深度基准面大地高L84后,结合各站位置,利用式(9)计算测量水域不同位置深度基准面的大地高,并根据式(11)实现PPK锚定/在航潮位向基于深度基准面潮高的转换。通过PPK基线解算和Tc=6 h潮位提取,得到C处的PPK潮位,借助上述基准转换关系,转换潮位站潮位为基于WGS84椭球面的大地高潮位,并以之为参考,评估PPK潮位测量成果的精度(如图 3所示)。统计结果表明,偏差最大值、最小值分别为13.5 cm和-14.4 cm,均值为0.8 cm,标准偏差为±6.5 cm。

|
| 图 3 锚定PPK潮位和传统潮位站潮位差分布 Fig. 3 Bias Distribution of Anchored PPK Tidal Level and Traditional Tidal Level |
基站位于A站,在ABC包围水域内开展走航 PPK潮位测量,基线长度30~76 km,历时约6 h。解算并提取Tc=4 h的PPK潮位如图 4(a)所示;根据A、B和C坐标及其观测潮位,距离加权内插获得在航不同位置的潮位,并借助上述建立的深度基准面与WGS84椭球面垂直基准间的转换模型,将内插潮位转换为大地高潮位,并与PPK在航潮位比较,误差曲线如图 4(b)所示。可以看出,二者具有很好的一致性,PPK潮位的最大偏差小于10 cm。

|
| 图 4 在航PPK潮位提取及与潮位站潮位比较 Fig. 4 On-the-Fly PPK Tidal Extraction and Comparison with the Tide from Tidal Station |
将基站分布位于A和B的不同测次的在航潮位采用上述类似处理,提取出在航PPK潮位,并将PPK走航潮位与基于传统潮位站潮位内插所得的经垂直基准转换模型转换的在航潮位进行比较,并统计分析各测次偏差的统计参数如表 3所示。从表 3中可以看出,整个在航潮位测量,最近距离为20 km,最远为90 km,PPK潮位的最大偏差均小于12 cm,大部分小于10 cm;偏差均值均为0.0,标准差均小于10 cm,取得了较高的潮位测量精度。同时也可以看出,随着PPK作用距离的增加,GPS基准站和流动站间的误差的相关性减弱,PPK潮位测量的精度降低。尽管如此,仍取得了偏差标准差优于8 cm的精度,从而也表明了本文给出的远距离潮位测量和提取方法、垂直基准确定及无缝转换模型构建方法的正确性。
| 基准站 | 时间长度/h | PPK潮位基线长度/km | 偏差/cm | |||
| 最大值 | 最小值 | 均值 | 标准差 | |||
| B | 6 | 20~65 | 7.6 | -7.5 | 0.0 | ±5.0 |
| B | 13 | 20~90 | 11.3 | -11.7 | 0.0 | ±7.7 |
| A | 9 | 30~76 | 7.5 | -7.9 | -0.0 | ±4.8 |
本文给出的20~100 km范围内的潮位测量方法以及垂直基准的确定和转换方法,解决了制约GPS远距离潮位测量的两大瓶颈问题,实现了远岸GPS潮位的准确获取及向基于平均海平面/深度基准面潮位的正确转换,并得到了实际工程的检验。在潮位提取中,截止周期需结合当地潮汐周期和工作状态进行选择,锚定状态下建议为当地潮汐周期的1/2,走航状态下为1/3~1/2;在潮位站,借助15~30 m GPS潮位测量,通过比较 即可获得该站高精度的L84;在远岸,开展2 d左右的锚定GPS潮位测量,结合岸边潮位站潮位,可实现优于10 cm的L和L84的确定精度。
| [1] | Zhao Jianhu, Clark J E H, Brucker S, et al. On-the-Fly GPS Tide Measurement Along Saint John River[J]. International Hydrographic Reviewer, 2004, 5(3):48-58 |
| [2] | Alkan R M. The Role of Pitch and Roll Effects on the Short Instantaneous Sea Level Height Determination with GPS[S/OL]. http://www.thsoa.org/pdf/h01/,2001 |
| [3] | Zhao Jianhu, Zhang Hongmei, John E. Hughes Clarke. Determination of Precise Instantaneous Tidal Level at Vessel[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12):1 067-1 070(赵建虎,张红梅,John E. Hughes Clarke. 测船处瞬时潮位的GPS精密确定[J]. 武汉大学学报·信息科学版,2006, 31(12):1 067-1 070) |
| [4] | Zhao Jianhu, Liu Jingnan, Zhou Fengnian. Method in Determining Vessel Attitude with GPS[J]. Journal of Wuhan Technical University of Surveying and Mapping,2000, 25(4):353-357(赵建虎,刘经南,周丰年.GPS测定船体姿态方法研究[J]. 武汉测绘科技大学学报,2000,25(4):353-357) |
| [5] | Zhao Jianhu, Zhang Hongmei. Determination of Precise Instantaneous Height at Multibeam Transducer[J]. Geo-spatial Information Science, 2007,10(4):250-254 |
| [6] | Ke Hao. Research on the Theory and Implementation Method of Marine Seamless Vertical Reference Surface[D]. Wuhan:Wuhan University, 2012(柯灏.海洋无缝垂直基准构建理论和方法研究[D].武汉:武汉大学,2012) |
| [7] | Bao Jingyang. On the Study of Vertical Datum for Hydrography and Cartography[J].Hydrographic Surveying and Charting,2009, 29(2):70-77(暴景阳.海洋测绘垂直基准综论[J].海洋测绘,2009,29(2):70-77) |
 2015, Vol. 40
2015, Vol. 40


