文章信息
- 钟何平, 张森, 田振, 唐劲松
- ZHONG Heping, ZHANG Sen, TIAN Zhen, TANG Jinsong
- 异构环境下的快速质量引导相位解缠算法
- A Fast Quality-guided Phase Unwrapping Algorithm in Heterogeneous Environment
- 武汉大学学报·信息科学版, 2015, 40(6): 756-760
- Geomatics and Information Science of Wuhan University, 2015, 40(6): 756-760
- http://dx.doi.org/10.13203/j.whugis20130518
-
文章历史
- 收稿日期:2013-09-22
相位解缠是干涉合成孔径雷达(interferometric synthetic aperture radar,InSAR)和干涉合成孔径声纳(interferometric synthetic aperture sonar,InSAS)信号处理中极其关键的步骤。相位解缠精度直接影响到InSAR 和InSAS 所生成的数字高程模型(DEM)的精度,它和解缠速度一起关系到InSAR 和InSAS 技术的应用与发展[1, 2]。理想情况下,相位解缠非常简单,而实际中由于低相干和地形突变等因素,使得部分区域不满足采样定理,相位解缠过程变得十分棘手。特别是当干涉相位维数大时,相位解缠速度将会严重制约干涉信号的处理效率[3, 4]。
目前,相位解缠算法主要分为三类:路径跟踪算法[5]、最小范数法[6]和网络流法[7]。在算法效率方面,路径跟踪法中枝切法和量化质量引导法较高,但是枝切法容易形成解缠“死区”。质量引导算法是基于这样一个假设:质量图可以引导积分路径,这些积分路径所围成的区域不包括未平衡的残差点。质量引导算法核心包含两个方面:①快速的质量引导过程;②高质量相位质量图生成。对于快速的质量引导,文献[5]提出了基于量化质量图和优先队列的快速引导策略,极大地优化了引导效率。为了提高质量引导算法的解缠精度,文献[8, 9]提出了新的质量图计算方法。但质量图的计算时间通常与其精度成正比,对于大维数干涉相位图的质量图计算,其计算时间在整个解缠过程中已占相当大的比重,严重制约着质量引导算法效率的进一步提升,并影响着干涉信号处理效率。而GPU的设计恰是以大量线程实现面向吞吐量的数据并行计算为目标,非常适合处理计算密度高、逻辑分支简单的大规模数据并行任务,这为实现快速质量图的计算提供了途径[10]。
本文提出了一种GPU和CPU运算相结合的异构环境质量引导算法。首先采用GPU计算相位质量图,由于质量图的计算属高密度计算型,因此可以达到较大的加速比。然后将质量图从显存载入内存,采用CPU进行量化质量引导,实现快速解缠相位求解。这种异构方式的相位解缠可以作为质量引导算法的一个基本框架,解决因质量图计算效率低下而影响解缠效率的问题。最后通过对InSAR和InSAS干涉数据的解缠试验,验证了所提算法的高效性。
1 算法描述 1.1 质量引导相位解缠算法
缠绕相位 φ(x,y)和解缠相位φ(x,y)之间的关系如下:
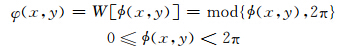
式中,W是缠绕运算。相位解缠就是从缠绕相位数组中恢复连续真实相位的过程。质量引导算法首先根据相位质量图选择一个高质量的像素点作为初始点,并检测它的4个邻近像素,对未解缠的邻近像素进行解缠,并存储到“邻近列”中。然后依次从“邻近列”中移除高质量像素点,并更新“邻近列”,重复以上过程,直至所有像素解缠完毕。为了加速质量引导过程,文献[5]提出了量化质量引导相位解缠算法,并取得了较好效果。
1.2 相位质量图并行求解
在干涉信号处理过程中,一般采用相干系数图作为干涉相位质量评价指标。在无法获得相干图时,常采用伪相关图、相位梯度变化图或最大相位梯度图作为相位质量的评价指标[1]。根据干涉相位计算相位质量值的过程是一个高密度的数值计算,这为采用GPU实现质量图的快速计算提供了途径。
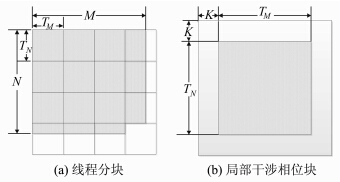
假设干涉相位图的行数和列数分别为M和N,计算点(m,n)处的质量采用的窗口大小为(2k+1)×(2k+1)。由于同一行或列相邻相位点的质量值计算将会用到(2k+1)×2k个相同相位点,为避免重复在显存中访问同一个相位点,减小访问延迟,先将干涉相位进行分块。每次计算前,将分块后的干涉相位载入共享存储器,由于共享存储器的访问速度远远大于显存的访问速度,可以显著提高计算效率。采用GPU计算相位质量图时,核函数以线程网格的形式组织,每个线程网格由若干个线程块构成,每个线程块又由若干线程组成,但不同GPU显卡对单个线程块内线程的个数限制不同。假设线程块的维数分别为TM和TN,则总线程块的行数和列数分别为BM=floor(M+TM-1/TM)和BN=floor(N+TN-1/TN),其中floor(x)表示取不大于x的整数,如图 1(a)所示。干涉数据的分块按照线程的分块进行,使得每个线程计算一个点的相位质量值。但由于计算相位点质量值时需要利用其周围点的相位值,因此载入局部干涉相位块时,还必须根据计算相位质量值所用的窗口载入其周围的相位数据,如图 1(b)所示,边界相位数据的宽度根据窗口大小确定,此时局部数据块的大小为(TM+k)×(TN+k)。
|
| 图 1 分块示意图 Fig. 1 Sketch Map of Blocking |
由于单个线程块的线程数小于局部数据块的数据个数,因此在载入局部干涉相位块时,部分线程需要载入多个数据。根据当前块线程的索引与局部相位块数据下标之间的关系,使得索引为(mod(Lx/TM),mod(Ly/TN))的线程装载局部相位块数据下标为(Lx,Ly)的干涉相位,这样可以保持数据装载过程中的负载均衡。由于线程之间的执行速度不可能完全一样,为了确保数据装载完毕之后才进行后续计算,这里需要采用syncthreads进行同步。
局部干涉数据装载进共享存储器后,线程块中的每一个线程根据自身索引计算与其对应的相位点质量值。由于在装载局部干涉数据时已经进行了边界扩展,这时不需进行边界的合法性判断,只需以当前点为中心,根据相应质量的定义计算质量值,然后将计算结果写入显存。
1.3 异构环境下的质量引导算法
质量引导算法主要由相位质量图计算和质量引导相位求解两部分组成。相位质量图计算是一种高密度数值型计算,适合采用 GPU进行并行求解。快速的量化质量引导过程是一种逻辑性很强的运算,它主要是采用优先队列来维护待解缠相位点的有序性,处理中涉及到大量的逻辑判断和出队、入队操作。这种逻辑性强的处理过程非常适合采用CPU计算。为了充分提升质量引导相位解缠算法的效率,在GPU和CPU的异构环境下求解,可以得到较大的加速比。
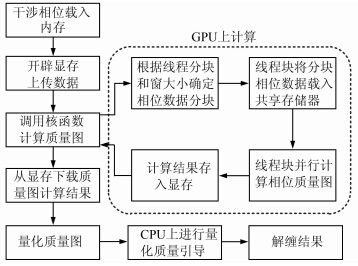
异构环境下的质量引导算法的工作流程如图 2所示。首先主机根据干涉相位参数调用CUDA函数在GPU中开辟显存空间,然后将干涉相位 上传至显存。设备端根据线程分块参数和计算窗口大小确定局部干涉相位的分块大小,每一个块在进行计算时,首先根据块索引将局部干涉相位载入共享存储器,然后块内线程并行计算每一点的相位质量值,计算完毕后,将计算结果存入显存。最后主机调用CUDA函数将计算的质量图结果从显存拷贝到本地内存,并将其量化到1~1 000之间的整数值。主机选择质量值最高的点作为解缠起始点,并采用量化质量引导策略求解最终的解缠结果。
|
| 图 2 异构环境下的质量引导算法流程 Fig. 2 Flow Chart of the Quality-guided Algorithm in Heterogeneous Environment |
为了验证所提异构环境下的质量引导相位解缠算法的性能,在如下环境进行了相位解缠试验:处理器Intel(R) Xeon(R) CPU X5650 2.67 G (2处理器12核),内存48 G,显卡Tesla C2050,操作系统Windows 7 专业版,软件环境VS2008+CUDA5.0。
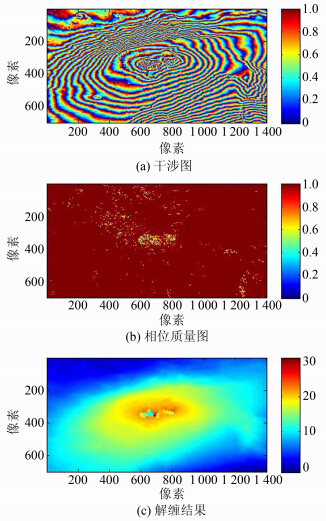
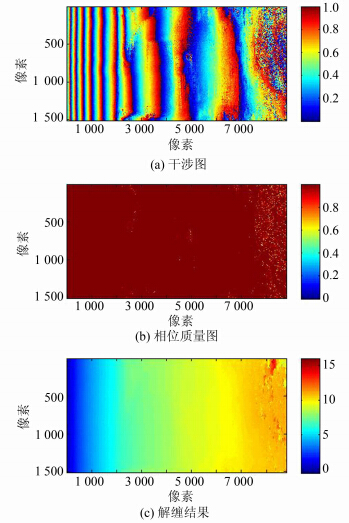
试验数据选用了Etna和InSAS干涉图,分别如图 3(a)和图 4(a)所示,其大小分别为1 400像素×700像素和1 512像素×8 800像素,残差点数分别为2 964个和24 652个。试验过程中,质量图选用可靠性较高的相位梯度变化质量图,计算质量图时,窗口大小设置为3×3,质量等级数取为1 000。从两幅干涉相位图对应的质量图图 3(b)和图 4(b)中可以看出,Etna干涉图的低质量区域集中在中部,InSAS干涉图的低质量区域集中在远距离处,它们给质量引导相位解缠带来了困难。采用GPU计算质量图时,线程块的维数设置为16×16,总的线程块数根据干涉相位数据的维数和单个线程块内线程的维数动态计算。
|
| 图 3 Etna干涉图解缠试验 Fig. 3 Unwrapping Test on Etna Interferogram |
|
| 图 4 InSAS干涉图解缠试验 Fig. 4 Unwrapping Test on InSAS Interferogram |
本试验中采用了三种质量引导相位解缠算法,分别是原始质量引导算法[1]、量化质量引导算法[5]和本文提出的异构环境下的质量引导算法,但是不同解缠方法的解缠结果都是相同的。两幅干涉图的解缠结果分别如图 3(c)和图 4(c)所示,可见,在低质量区域存在一定的误差累积传播现象,这是质量引导算法无法避免的,但可以通过设计更可靠的相位质量图来对误差传播进行有效的抑制。
表 1给出了两幅干涉图在GPU上的计算时间分布情况。可以看出,Etna干涉图的数据传输时间为数据上传时间和数据下载时间之和,共计2.3+2.1=4.4 ms,核函数执行时间为4 ms,两者分别占总计算时间的52.4%和47.6%。对于大维数InSAS干涉图,数据传输时间为21.4+22.3=43.7 ms,核函数执行时间为52.2 ms,两者分别占质量图总计算时间的45.6%和54.4%。通过比较可以发现,在计算质量图时,数据计算与数据传输时间几乎相当,因此数据传输速度在质量图的并行计算过程中起着非常重要的作用。
| 干涉图 | 数据上传时间/ms | Kernel函数执行时间/ms | 数据下载时间/ms | 总计算时间/ms | 执行时间/% | 数据传输/% |
| Etna | 2.3 | 4 | 2.1 | 8.4 | 47.6 | 52.4 |
| InSAS | 21.4 | 52.2 | 22.3 | 95.9 | 54.4 | 45.6 |
三种质量引导算法的解缠效率比较结果如表 2所示。原始质量引导算法所需的解缠时间最长,对于Etna和InSAS两幅干涉相位图的解缠时间分别为57 985 ms和670 427 ms,因此远远不能满足实时相位解缠的需要。采用量化质量引导策略优化质量引导过程后,对Etna干涉图的质量引导时间从57 677 ms减小到283 ms,使得总解缠时间降为591 ms,加速比达到98.1。InSAS干涉图的质量引导时间从666 650 ms减小为3 252 ms,总的解缠时间降为7 035 ms,加速比达到95.3。进一步采用GPU并行计算后,Etna干涉图的质量图计算时间由307 ms减为8.4 ms,InSAS干涉图的解缠时间由3 783 ms减为95.9 ms,加速比也分别由98.1、95.3提升到199.7和200.4,异构环境下总的解缠时间分别减为290.4 ms和3 345.9 ms。
| 干涉图 | 解缠方法 | 质量图计算时间/ms | 质量引导时间/ms | 总计算时间/ms | 加速比 |
| Etna | 原始算法 | 308 | 57 677 | 57 985 | 1 |
| 量化质量引导算法 | 307 | 283 | 591 | 98.1 | |
| 本文算法 | 8.4 | 282 | 290.4 | 199.7 | |
| InSAS | 原始算法 | 3 777 | 666 650 | 670 427 | 1 |
| 量化质量引导算法 | 3 783 | 3 252 | 7 035 | 95.3 | |
| 本文算法 | 95.9 | 3 250 | 3 345.9 | 200.4 |
本文提出了一种异构环境下的快速质量引导算法,在保持相位解缠精度的同时,极大地提高了相位解缠速度。首先采用GPU进行相位质量图计算,充分发挥GPU的高密度计算能力。然后将质量图下载到主机内存,采用CPU进行量化质量引导,利用CPU的逻辑运算优势求解最终的解缠结果。试验结果表明,该算法充分利用了异构环境优势,大幅度提高了质量引导算法的效率,满足实时系统的应用需求。为进一步提升质量算法的效率,还需要在质量图并行计算优化和质量引导过程的并行化两个方面进行深入研究。
| [1] | Ghiglia C D,Pritt D M.Two-dimensional Phase Unwrapping:Theory, Algorithm, and Software[M].New York:John Wiley & Sons Inc,1998 |
| [2] | Xu Caijun, Wang Hua. Comparison of InSAR Phase Unwrapping Algorithms and Error Analysis[J]. Geomatics and Information Science of Wuhan University, 2004, 29(1):67-71(许才军, 王华. InSAR 相位解缠算法比较及误差分析[J]. 武汉大学学报·信息科学版, 2004, 29(1):67-71) |
| [3] | Carballo G F.Statistically-based Multiresolution Network Flow Phase Unwrapping for SAR Interferometry[D].Sweden:Kungliga Tekniska Hogskolan,2000 |
| [4] | Chen C W.Statistical-cost Network-flow Approaches to Two-dimensional Phase Unwrapping for Radar Interferometry[D].California:Stanford University,2001 |
| [5] | Zhong Heping, Tang Jinsong, Zhang Sen, et al. A Fast Phase Unwrapping Algorithm Based on Quantized Quality Map and Priority Queue[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3):342-345(钟何平,唐劲松,张森,等.利用量化质量图和优先队列的快速相位解缠算法[J]. 武汉大学学报·信息科学版,2011,36(3):342-345) |
| [6] | Chen Qiang, Yang Yinghui, Liu Guoxiang, et al. InSAR Phase Unwrapping Using Least Squares Method with Integer Ambiguity Resolution and Edge Detection[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(3):441-448(陈强,杨莹辉,刘国祥,等.基于边界探测的InSAR最小二乘整周相位解缠方法[J]. 测绘学报,2012,41(3):441-448) |
| [7] | Costantini M. A Phase Unwrapping Method Based on Network Programming[C]. Fringe'96 Workshop-ERS SAR Interferometry, Zurich,1996 |
| [8] | Cho B L,Kong Y K,Kim Y S.Quality Map Extraction for Radar Interferometry Using Weighted Window[J].Electronics Letters,2004,40 (8):472-473 |
| [9] | Quan C,Tay C J,Chen L, et al.Spatial-Fringe-Modulation-based Quality Map for Phase Unwrapping[J].Applied Optics,2003,42 (35):7 060-7 065 |
| [10] | Xiao Han, Zhang Zuxun. Parallel Image Matching Algorithm Based on GPGPU[J]. Acta Geodaetica et Cartographica Sinica,2010,39(1):46-51(肖汉, 张祖勋.基于GPGPU的并行影像匹配算法[J]. 测绘学报,2010,39(1):46-51) |
 2015, Vol. 40
2015, Vol. 40


