文章信息
- 陈金磊, 康志忠
- CHEN Jinlei, KANG Zhizhong
- 高分辨率三维激光扫描数据的微小变形统计分析
- A Statistical and Analytical Method for Detecting Tiny Deformations in High Resolution 3D Laser Scanning Data
- 武汉大学学报·信息科学版, 2015, 40(6): 744-750
- Geomatics and Information Science of Wuhan University, 2015, 40(6): 744-750
- http://dx.doi.org/10.13203/j.whugis20130358
-
文章历史
- 收稿日期:2013-07-27
近年来,三维激光扫描技术的出现为测绘人员提供了一种新的获取空间信息的技术手段。三维激光扫描数据是由高精度的扫描仪获得的,具有高精度的三维点云,国内外学者对其用于监测变形已进行了一定的研究,Gosliga[1]采用拟合模型的方式,利用曲面参数拟合研究隧道变形,克服了单点精度低的缺陷,提高了监测精度;Alba等[2]用同样的方法对大坝进行了监测;吕钊等[3]采用三维点云数据转化成二维的反射值影像,然后利用尺度不变特征变换(scale-invariant feature transform,SIFT)进行特征点匹配,比较了两期点云数据的变化来检测建筑模型的变化;Lindenbergh[4]通过获得高精度的点云数据来得到精确的变形。但是以往的研究都是认为拼接误差很小或为0的前提下得到的变形量,但当变形小于测量误差时,变形是无法反映出来的。
偶然误差及拼接误差是必然存在也是无法消除的,但通过减小偶然误差及拼接误差的影响,反映微小变形成为可能,对此,本文提出利用SIFT算法与贝叶斯抽样一致性算法(Bayes sample consensus,BaySAC)对反射值影像特征点进行精确提取,迭代最近点算法(iterative closest point,ICP)精确拼接来提高拼接精度;采用随机抽样一致性算法(random sample consensus,RANSAC)剔除粗差,进而提高拟合的精度。在此基础上,通过格网化方法[5]消弱偶然误差的影响,修正拼接误差,反映变形。
1 基于反射值影像和BaySAC的点云拼接方法
本文提出了基于反射值影像和BaySAC的点云拼接方法。首先通过点云数据生成反射值影像[3],然后利用SIFT算子进行影像匹配,针对可能存在的误匹配,利用BaySAC算法[6]进行剔除。BaySAC是基于RANSAC算法思想的改进算法,利用局内点概率来选取抽样样本集。本文对先验局内点概率的估计是利用基于随机概率U(0,1)的估计方法,选取基于随机概率U(0,1)分布的随机值作为对同名点的先验概率,而假设检验模型是空间直角坐标系之间的坐标转换模型。
通过匹配的同名点对计算变换参数,实现点云数据的粗拼接,然后采用迭代最近点(iterative closest point,ICP)算法进行精拼接,从而提高点云数据的拼接精度。
2 微小变形统计分析方法
对变形统计的方法主要有以下4种:① 两期数据拟合的参数比较法[7],此方法可以了解两期数据整体的变化情况;② 两期数据对应点距离法,该方法通过建立对应关系,统计对应点的距离来衡量数据之间的变化;③ T 统计量[4, 8],通过拟合参数之间的变化来整体了解变化情况;④ 格网化处理[1, 9]。将数据进行格网化,形成小格网点集,减小每格网点集偶然误差的影响,统计所有格网点集的变化量。本文主要是应用质量检测T值及格网化处理两种方法。
由于点云数据量大,为了提高运算效率,本文通过截取监测数据中的平面或曲面来描述变形问题。三维点云数据中存在着噪声点,如果在截取的区域中存在噪声点,将严重影响本文微小变形统计实验的灵敏性,因此,本文通过RANSAC算法来剔除噪声点,提高拟合精度。
2.1 基于RanSAC的平面或曲面拟合
RANSAC算法[10]的优点是稳定、可靠、精度高,对噪声有很好的承受能力,鲁棒性强,具有较好的剔除粗差点的能力,其步骤如下。
1)从原始数据中随机抽取n对同名点来计算两期数据的转换参数,n为拟合模型的最少同名点个数。
2) 根据上述产生的转换参数来计算符合此参数阈值的同名点。
3) 重复上述过程,直到得到符合模型的最大点集。
本文通过RANSAC算法来剔除噪声点,然后应用最小二乘法来拟合,得到高精度的拟合参数[7]。
平面模型为:
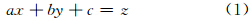
曲面模型为:

以平面模型为例,其参数X = a,b,c ,模型残差为e,因此,方程(1)写成矩阵形式为:
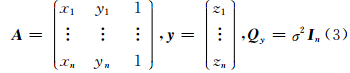
得到:
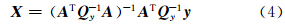
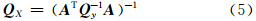

其中,Q y为观测值的协方差矩阵;σ为单点中误差;In为n阶单位向量;Q X为X 的协方差矩阵,表现参数之间的相关性,如果参数之间不相关,则QX呈直线,而对角线两侧的值很小[9]。
拟合精度的评定是采用点距法[11, 12],根据点到拟合平面的距离d计算中误差。精度公式为:
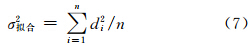
虽然提高拼接及拟合精度有利于变形的检测,但是拼接误差与偶然误差的存在依然影响微小变形的检测,因此,需要对偶然误差及拼接误差进行统计分析,减小其影响。
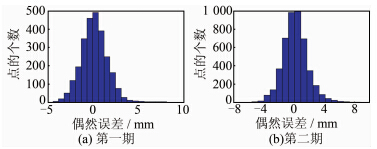
2.2 偶然误差的统计分析 2.2.1 偶然误差检测
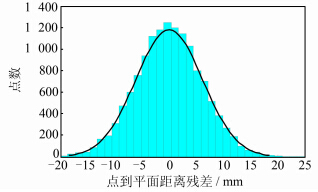
由于仪器本身的原因,点云数据存在偶然误差,通过点云数据到其拟合面的有向距离来检测偶然误差的分布情况。如果分布符合正态分布的特征,则认为是偶然误差。
根据随机误差的特点可知,正态分布的特征[11]为:在一定的观测条件下,误差的绝对值超出一定限值的误差,其出现的概率为零;绝对值较小的误差比绝对值较大的误差出现的概率大;绝对值相等的正负误差出现的概率一致;偶然误差的数学期望为零,即

由于偶然误差存在的特征,可以通过拟合的方式对偶然误差进行检测(图 1),将点云数据按一定的区间边长划分为小格网点集,对每一个小格网点集取平均值,消弱偶然误差的影响。
|
| 图 1 正态分布的特征 Fig. 1 Characteristics of Normal Distribution |
格网化原理如下:首先对截取的点云数据求其到拟合平面的距离Hi,然后进行格网化[8],每一小的格网边长大约为l(单位:m),可分为 m个小格网。对每格网取平均值,作为该格网的值Gj,这样可以减小偶然误差的影响。将这些值根据格网的位置呈现在平面上,可以直观地查看误差的变化情况,然后求得数学期望为:

标准差为:

格网边长的大小还没有一个明确的标准既保持数据之间的关联信息,又减小偶然误差的影响。如果选得太小,偶然误差不能有效的减小;选得太大,又可能在直观的表现效果上不佳。
2.3 拼接误差检测方法
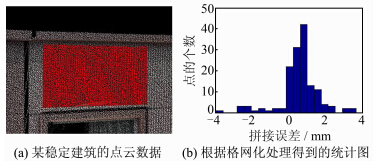
对整个场景拼接后,认为变形区域附近的稳定建筑数据(如早期的建筑)中只存在偶然误差及拼接误差,不存在变形。因此在稳定的建筑上截取对应的两期数据来检定拼接误差,同时对两期数据进行格网化处理,两期数据中对应的格网小点集平均值之间的距离即为该小格网的平均拼接误差,然后对整个截取面的格网进行统计,得到拼接误差。
图 2(a)为某稳定建筑的点云数据,图 2(b)为根据格网化处理得到的统计图。
|
| 图 2 拼接误差检测 Fig. 2 Registration Error Detection |
通过减弱偶然误差的影响,使得第二期数据到第一期数据的距离的变化范围为-4~5 mm,根据图 2(b),拼接误差主要集中在0~2 mm,其均值为0.856 8 mm;而没有消除偶然误差时的变化范围为-30~30 mm,对其取均值为1.016 4 mm。可见,消弱偶然误差可以提高检测精度。这样将拼接误差检测出来,进一步检测变形的大小。
2.4 变形检测方法
T统计量是可以用于假设检验,根据拟合模型计算用来做检验的统计量。正常的T应该在0假设为真时,服从T分布,而本文是用来预检测两期数据是存在变形还是稳定的。
方法如下:根据拟合平面得到的参数,第一期数据参数 X 1=(a1,b1,c1),协方差矩阵为 Q X,1;第二期数据参数为 X 2=(a2,b2,c2),协方差矩阵为 Q X,2。设
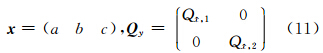
通过实验统计T= e T Q y e /(m-k)判断两个拟合平面的模型拟合度。其中,e 为模型的残差,m=6表示观测值的个数,k=3表示参数的个数。T值是用来检测两期的参数对A模型的拟合情况。这样通过T值来衡量拼接误差的大小,就需要一个阈值Kα[6]来检测拼接的效果。阈值Kα的求解如下:
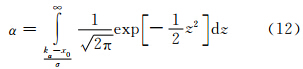
如果T < Kα,说明两期数据的变化在容许范围内,可以认为没有变化;反之,则说明存在变形。
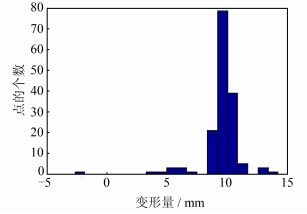
预处理后需要反映出变形情况,根据在稳定部位检测出的拼接误差,则认为变形区域同样存在相同的拼接误差。在此前提下,检测变形方法为:截取变形区域数据,以第一期数据为参考拟合面,对第二期数据进行格网化处理,计算每格网平均值到参考拟合面的距离,此时认为此距离中的偶然误差基本消除,然后将检测得到的拼接误差代入,即消弱了拼接误差的影响,得到变形量。图 3显示了修正拼接误差后变形量的统计情况,对统计的变形量取均值,作为变形区的变形量。
|
| 图 3 消除拼接误差后的统计图(简易楼) Fig. 3 Statistics After Eliminating Registration Errors |
本文共进行了三组实验,第一组来自首都师范大学简易楼,数据采集是通过 Riegl LMS-Z620三维激光扫描仪获取的,仪器测量距离范围为2~2 000 m,单点测量精度为10 mm。另外两组实验分别为涪陵五中教学楼及上海地铁隧道,数据采集是通过Riegl LMS-VZ400三维激光扫描仪获取的,仪器测量距离范围为1.5~600 m,单点测量精度为5 mm。实验的实景如图 4所示,实验数据说明可见表 1。

|
| 图 4 实景图 Fig. 4 Real Scene |
| 简易楼 | 教学楼 | 地铁隧道 | |
| 水平角/(°) | 84.55~ 259.1 | 0.0~359.9 | 0.00~ 359.95 |
| 竖直角/(°) | 50.6~ 129.5 | 50.0~ 129.8 | 30.00~130.05 |
| 距离范围/m | 5~50 | 3~100 | 2~82 |
| 角度分辨率/(°) | 0.045 | 0.075 | 0.115 |
本文的精度分析是根据手动拼接及影像提取同名点比较来衡量的,如表 2所示。
| 同名点/个 | 中误差/m | 格网化处理/m | T值 | ||
| 简易楼 | RISCAN PRO | 8 | 0.009 | 0.009 7 | 0.042 3 |
| BaySAC | 56 | 0.000 76 | 0.002 4 | 0.012 5 | |
| 教学楼 | RISCAN PRO | 10 | 0.008 7 | 0.001 7 | 0.046 |
| BaySAC | 175 | 0.002 4 | 0.001 5 | 0.041 |
利用反射值影像提取同名点的方式,在点云数据中可以得到更多的同名点,得到比RISCAN PRO 软件中更准确的转换矩阵。
3.2 微小变形量统计实验 3.2.1 拟合精度分析
选取存在噪声点的点云数据,红色区域内的黑色点云为噪声点。用最小二乘法及RANSAC算法分别进行拟合,如图 5所示。

|
| 图 5 两种拟合方法的效果图 Fig. 5 Results of Fitting |
图 5中,最小二乘法未达到实验需要的平面,而RANSAC算法剔除噪声,根据平面参数对点云数据进行平面拟合,效果明显比最小二乘法好。在拟合点云数据中均匀地选择10个点,根据到拟合平面的距离来检验拟合的精度。
表 3中,同样的位置选择的点,应用最小二乘法得到的点面距离最大为0.049 m,最小为0.012 m;而RANSAC算法得到的最大的点面距离为-0.000 8 m,说明RANSAC算法来拟合数据可以提高拟合的精度。
| 点号 | 点面距离/m | 点号 | 点面距离/m | ||
| 最小二乘法 | RANSAC 算法 | 最小二乘法 | RANSAC 算法 | ||
| 1 | -0.018 5 | -0.000 8 | 6 | -0.018 0 | 0.000 1 |
| 2 | -0.027 3 | 0.000 2 | 7 | 0.015 8 | 0.000 01 |
| 3 | 0.012 9 | 0.000 2 | 8 | 0.049 7 | 0.000 7 |
| 4 | -0.012 7 | -0.000 4 | 9 | -0.016 9 | -0.000 2 |
| 5 | 0.014 9 | 0.000 1 | 10 | 0.036 8 | -0.000 2 |
在基于反射值影像和BaySAC的点云拼接方法提高拼接精度,利用RANSAC算法剔除粗差,提高拟合精度的前提下,对微小变形进行统计分析。
1)偶然误差分析及消弱
在拼接后的两期点云数据截取方位相同的数据,对两期点云进行偶然误差检测,综合地评定偶然误差的影响。简易楼实验中选择的点云数据范围为 2.7 m × 1.2 m,第一期数据共有11 888个点,第二期数据有19 986个点。教学楼实验中截取的点云数据为2.18 m × 1.18 m,第一期数据共有21 247个点,第二期数据有28 664个点。在地铁隧道实验数据的顶部截取数据,第一期数据截取2 610个点,第二期数据截取4 714个点,范围为2.0 m × 0.8 m。图 6所示为实验截取的点云数据。

|
| 图 6 截取的点云数据 Fig. 6 Intercepted Points Cloud |
对于偶然误差的检测,通过点到拟合平面的距离来统计,得到的结果如图 7所示。
|
| 图 7 点云数据偶然误差统计图(地铁隧道) Fig. 7 Random Error of Points Cloud |
简易楼实验中,两期点云数据的偶然误差的 中误差分别为-0.041 2 mm及0.031 8 mm;教学楼实验中,两期点云数据的偶然误差的中误差分别为0.015 0 mm及0.014 0 mm;地铁隧道实验中,两期数据的偶然误差的中误差分别为0.143 5 mm及0.215 3 mm。实验结果表明,实验对象的偶然误差符合正态分布特征(图 1)。因此要消除偶然误差的影响,根据格网化处理方法,得到实验楼、教学楼及圆形隧道的第二期数据到第一期拟合平面的距离分布图及统计图。
图 8(a)、8(b)分别为格网化处理、消弱偶然误差后第二期点云数据到第一期拟合面的距离分布及统计情况。可以看出,变化量主要集中在某值(2 cm)左右,而边缘的点只有少数的几个,因此可以用均值来体现拼接误差的大小。

|
| 图 8 第二期数据到第一期拟合曲面的距离(地铁隧道) Fig. 8 Distance Between the Data of Second Epoch and the Fitting Plane of First Epoch |
表 4显示了消弱偶然误差前后两期数据的距离变化范围及处理后距离的均值,表明格网化处理对消弱偶然误差的影响有很大的作用。消弱偶然误差后,进一步地检测拼接误差。
| 含偶然误差 | 格网化处理 | 均值 | |
| 简易楼 | -30~30 | -3~5 | +0.856 8 |
| 教学楼 | -5~15 | 0~4 | +2.566 9 |
| 地铁隧道 | -40~20 | -10~5 | +1.865 2 |
2)拼接误差的检测
当消弱偶然误差以后,稳定部位两期数据中只存在拼接误差的影响。依照格网化处理的方法,用统计的方式来得到拼接误差。表 5显示了三组实验格网化处理后拼接误差的大小。三组实验中得到的数学期望认为是拼接误差的大小,然后再对变形进行检测。
| 中误差 | 标准差 | |
| 简易楼 | +0.856 8 | 0.037 2 |
| 教学楼 | +2.566 9 | 0.014 3 |
| 地铁隧道 | +1.865 2 | 0.057 2 |
3)变形的检测
在变形区域附近截取平面或曲面进行变形检测,如图 9所示。

|
| 图 9 截取点云数据 Fig. 9 Intercepted Points Cloud |
在本文中,首都师范大学的简易楼第一期数据是在简易楼建设中采集的数据,而第二期为建设完成后采集的数据,因此将新建的简易楼涂漆前与涂漆后的差异作为变形,进行统计分析。为了更具有说明性,有助于实验比较,人为地对涪陵五中教学楼立面的法向方向及上海地铁隧道数据的垂直沉降方向设定+2 mm的变形量。
对拼接误差进行修正,利用质量检测T值来预检测修正后的两期数据是否存在变形。当对
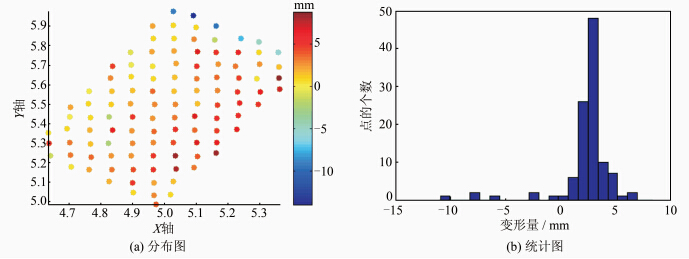
两期数据的拟合平面进行质量检测时,首先进行阈值的设定,设可靠性水平 α=0.001,σ=0.005 m, x0 = 0.0 m,Kα=0.006。简易楼实验的检测值T=0.054 1 ,教学楼实验的检测值T=0.009 4,地铁隧道实验的检测值T=0.011 2,均大于Kα,表明三组实验数据的变化超出检测的范围。所以消除偶然误差及拼接误差后,数据还存在着变形。图 10为三组实验修正误差后消除偶然误差前后的分布情况。
|
| 图 10 消除拼接误差后的分布图(地铁隧道) Fig. 10 Circular Tunnel Distribution After Eliminating Registration Errors |
根据图 10、表 6 的结果显示,在简易楼实验中,应用本文方法得到的变形量为+9.186 mm,而直接采用两期数据求得的差异值显示的变形量为+12.193 mm;在加入变形为2 mm的情况下,教学楼实验比实际变形大0.64 mm,而地铁隧道实验的结果比实际的变形大0.473 mm。而不经过统计分析,直接采用两期数据求得的差异值显示的变形量要比格网化处理的结果大很多,可见,本文采用的方法是有效的。
| 距离变化范围 | 变形统计结果 | |||
| 含偶然误差 | 消除偶然误差 | 格网化处理 | 差异量 | |
| 简易楼 | -30~30 | -2~14 | +9.186 | +12.193 |
| 教学楼 | -5~15 | 0~4.5 | +2.627 | +5.442 |
| 地铁隧道 | -40~20 | -10~5 | +2.473 | +4.282 |
| 注: 变形统计结果中,对于简易楼及教学楼是立面建筑,“+”表示凸出;而对于地铁隧道,“+”表示为下沉。 | ||||
本文针对海量的点云数据,提出了利用高分辨率三维激光扫描数据的微小变形统计分析方法。通过基于反射值影像和BaySAC的点云拼接方法提高拼接精度,RANSAC算法剔除粗差,提高拟合精度,进而利用格网化处理的方法减小偶然误差的影响,统计拼接误差,用质量检测值T对修正拼接误差后的数据预检测,当T大于阈值时,再对修正后的数据提取变形量。实验结果表明,该方法对微小变形统计分析有很好的效果。
变形量的检测最重要的是对拼接误差的检测分析,而本文是采用附近的拼接误差做改正的近似方法,下一步的工作是对拼接误差的检测分析进行进一步研究。而且本文中描述的变形只对一个面的整体形变进行统计,今后的工作将对三维方向上的变形进行统计。
| [1] | Van Gosliga R, Lindenbergh R,Pfeifer N. Deformation Analysis of a Bored Tunnel by Means of Terrestrial Laser Scanning[J]. IASPRS, 2006,36(5):167-172 |
| [2] | Alba M, Fregonese L, Prandi F, et al. Structural Monitoring of a Large Dam by Terrestrial Laser Scanning[J].International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences,2006,36(5):5 866-5 883 |
| [3] | Lv Zhao,Kang Zhizhong.Change Detection of Buildings Based on Terrestrial Laser Scanning Data[J]. Geomatics and Information Science of Wuhan University,2011,36(11):1 284-1 289(吕钊,康志忠.利用地面激光扫描数据进行建筑物变化检测[J].武汉大学学报·信息科学版,2011,36(11):1 284-1 289) |
| [4] | Lindenbergh R, Uchanski L, Bucksch A, et al. Structural Monitoring of Tunnels Using Terrestrial Laser Scanning[J]. Geodesy, 2009, 87(2):231-239 |
| [5] | Lu Xiushan,Huang Lei.Grid Method on Building Information Extraction Using Laser Scanning Data[J]. Geomatics and Information Science of Wuhan University, 2007,32(10):852-855(卢秀山,黄磊.基于激光扫描数据的建筑物信息格网化提取方法[J].武汉大学学报·信息科学版,2007,32(10):852-855) |
| [6] | Jia Fengman,Kang Zhizhong,Yu Peng. A SIFT and Bayes Sampling Consensus Method for Image Matching[J]. Acta Geodaetica Cartographica Sinica, 2014,42(6):877-883(贾丰蔓,康志忠, 于鹏. 基于SIFT算法与贝叶斯抽样一致性检验的影像同名点匹配[J].测绘学报,2014,42(6):877-883) |
| [7] | Zhou Chunlin, Zhu Hehua, Li Xiaojun. Research and Application of Robust Plane Fitting Algorithm with RANSAC[J]. Computer Engineering and Application,2011,47(7):177-179(周春霖,朱合华,李晓军.随机抽样一致性平面拟合及其应用研究[J].计算机工程与应用,2011,47(7):177-179) |
| [8] | Teunissen P. Testing Theory:An Introduction[M]. Delft:Delft University Press, 2000 |
| [9] | Lindenbergh R, Pfeifer N.A Statistical Deformation Analysis of Two Epoches of Terrestrial Laser Data of a Lock[C]. The 7th Conference on Optical 3D Measurement Techniques, Vienna, Austria, 2005 |
| [10] | Tom B, Steven M, Richard G. New Conditional Sampling Strategies for Speeded-Up RANSAC[C]. British Machine Vision Conference, London, UK, 2009 |
| [11] | Group of Surveying and Mapping Survey Adjustment.Error Theory and Measurement Adjustment Basis[M]. Wuhan:Wuhan University Press,2008(武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉:武汉大学出版社,2008) |
| [12] | Cai Lailiang,Wu Kan, Zhang Shu. Application of Point Cloud Fitting to Deformation Monitoring Using 3D Laser Scanner[J]. Science of Surveying and Mapping, 2010,35(5):231-232(蔡来良,吴侃,张舒.点云平面拟合在三维激光扫描仪变形监测中的应用[J].测绘科学,2010,35(5):231-232) |
 2015, Vol. 40
2015, Vol. 40


