文章信息
- 张晓平, 边少锋, 李忠美
- ZHANG Xiaoping, BIAN Shaofeng, LI Zhongmei
- 极区高斯投影与日晷投影的比较
- Comparisons Between Gauss and Gnomonic Projections in Polar Regions
- 武汉大学学报·信息科学版, 2015, 40(5): 667-672
- Geomatics and Information Science of Wuhan University, 2015, 40(5): 667-672
- http://dx.doi.org/10.13203/j.whugis20140128
-
文章历史
- 收稿日期:2014-02-22
2. 海军工程大学导航工程系, 湖北 武汉, 430033
2. Department of Navigation, Naval University of Engineering, Wuhan 430033, China
随着极区越来越受到国际的关注,我国也日益重视极区考察工作。选择合适的投影方式对绘制极区地形图或航行所需航海图至关重要[1, 2, 3]。日晷投影是常用于高纬度地区航行的一种投影方式,它的主要特点是大圆航线在投影面上表现为直线,不过它是任意投影,即无论是方向上还是距离上都有较复杂的变形[4, 5, 6]。高斯投影在中央经线附近变形较小且具有保角性质,常被我国作为地形图的数学基础[7, 8]。但是,传统的高斯投影常被表示为分带形式,使得地球被分成以南北极为端点的多条狭窄条带。针对这种情况,国内学者曾推导出高斯投影复变函数表示式,该表达式使得高斯投影不再受限于带宽,但由于等量纬度在极区的奇异性导致投影公式在极区难以应用[9, 10]。鉴于此,文献[11]曾推导出球面高斯投影与横轴墨卡托投影的等价性,则可得球面高斯投影的闭合公式。该闭合公式虽形式紧凑且不受限于带宽,却在极区出现奇异现象。因此,本文以高斯投影闭合公式为基础,推导了可用于南极与北极地区的球面高斯投影极区非奇异公式,并基于该公式对极区高斯投影进行变形分析及一些重要方程的推算。最后,与日晷投影进行比较,可知极区非奇异高斯投影公式可为极区地图的绘制提供重要参考。
1 高斯投影极区非奇异公式及日晷投影公式
考虑到球面高斯投影与横轴墨卡托投影的等价性,则球面高斯投影公式可表示为:
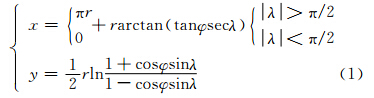
式中,r、 φ,λ 与(x,y)分别表示地球半径、点的球面坐标及其在投影平面上的坐标。由式(1)易知,当φ→π/2,tanφ→∞时,投影公式存在奇异,这就使得极区投影具有不连续的特点。此外,采用该公式在极区进行作图时还要考虑λ的取值而选择不同的投影公式。
为解决该公式的奇异问题,将投影后的极点作为原点,可得式(2):
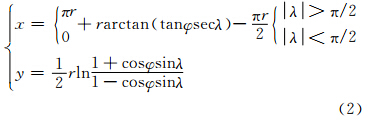
记θ=π/2-φ,考虑λ的范围及满足反三角函数相互关系的条件,分别针对式(2)中x方向的投影公式进行讨论。
当 |λ |<π/2时,有secλ>0,即tanφsecλ>0,利用关系arctanx=π/2-arccotx及当x>0时,有arctanx=arccot 1/x ,此时,
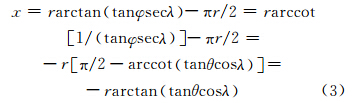
当 |λ |>π/2时,secλ<0,即tanφsecλ<0,此时,利用关系式arctanx=arccot 1/x 以及arctanx=-arctan -x ,可对x作如下变形:

由式(3)、(4)可以看出,针对不同范围的λ,其改进后x方向投影公式经简化后是连续统一的,且该投影公式在极区范围内不存在奇异点,克服了传统公式在极点奇异的缺点。
另外,在极区范围内,有 cosφsinλ <1,利用反双曲正切函数的定义及其对数表达式y=ln[(1+x )/(1-x)]/2 |x |<1 ,可以得到y=arctanhx,可对y方向投影公式作如下变形:
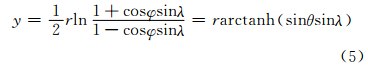
即得极区高斯投影非奇异公式,可统一表示为:

从式(6)可以看出,改进后的投影公式在极区已不存在奇异问题,而且满足极区高斯投影公式统一,而无需分别考虑λ的范围。以0°E为中央经线,可借助Geocart软件绘制出以极点作为投影平面中心的极区连续投影图,如图 1所示。

|
| 图 1 北极圈内高斯投影示意图 Fig. 1 Diagram of Gauss Projection in Arctic Circle |
根据文献[8]可知,日晷投影是视点位于球心的透视投影,它的投影公式为:

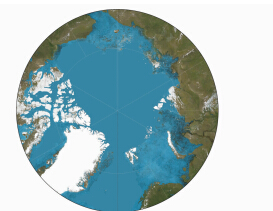
同样地,借助Geocart软件可绘制出北极圈内的日晷投影示意图,如图 2所示。
|
| 图 2 北极圈内日晷投影示意图 Fig. 2 Diagram of Gnomonic Projection in Arctic Circle |
由图 1、2可以看出,采用高斯投影及日晷投影分别将地球表面投影至平面上,在北极圈范围内,这两种投影的效果很相似,它们的经纬网形状非常接近,即高斯投影的经线近似为直线,纬线圈近似为圆形。
为验证这两种投影在极点附近非常接近,可借助计算机代数系统[12]将两种投影的公式展开成关于余纬度 θ的幂级数形式,整理后可得高斯投影公式表示为:

相应地,日晷投影公式可表示为:

对式(8)、(9)进行对比可以发现,将两种投影的公式展开成关于余纬度θ的幂级数形式后,两种投影对应坐标的主项相等,其中,纵坐标展开式中的第二项差异值为θ3cos3λ/3,相应横坐标的第二项差异值为θ3(-3sinλ+sin3λ)/6。由此可知,当余纬度很小时,这两种投影对应的坐标值很接近。当余纬度保持不变时,点越靠近中央子午线,两种投影的纵坐标差异值越大,而对应横坐标差异值越小。
2 极区高斯投影与日晷投影的比较 2.1 极区高斯投影经纬线方程
在平面上建立经纬网作为地图的数学基础,是研究地图投影的首要目的。根据极区高斯投影非奇异公式,可以推导出极区经纬线投影方程。将式(6)做如下变形:

顾及到对任意λ都有cos2λ+sin2λ=1,将式(10)中与λ有关的量移到方程式一边,两等式经平方后求和,即可得纬线圈投影方程:

利用计算机代数系统可绘制纬线圈的投影示意图(见图 3)。

|
| 图 3 极区高斯投影纬线圈和子午线示意图 Fig. 3 Diagram of Parallels and Meridians of Gauss Projection in Polar Regions |
同理,顾及到对任意θ值都有csc2θ-cot2θ=1,将式(10)方程式中与θ无关的量移到等号左边,两等式取倒数后平方再相减,即可以求出子午线投影方程:

根据式(12),可利用计算机代数系统绘制出极区投影后子午线(λ间隔 15°)(见图 3)。如式(11)、(12)所示,在高斯投影中,纬线圈的投影方程形如椭圆方程,而子午线投影方程形如双曲线方程。而由图 3可以看出,在极区范围内纬线圈的形状类似扁率很小的椭圆,而子午线表示为以极点向外发散并向中央子午线靠拢的一组曲线。特别地,在余纬度很小时子午线近似为直线。 2.2 长度变形比较
高斯投影为等角投影,即从任一点出发,各方向的长度比是相等的,因此,任一方向长度比即是该点处的长度比。根据文献[8]中长度变形的定义,略去推导,可得极区高斯投影长度变形公式:
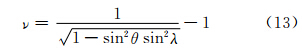
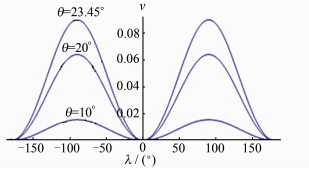
为更直观了解极区范围内高斯投影的长度变形,利用计算机代数系统求出极区范围内的几个重要纬度θ=0°、10°、20°以及23.45°(极圈)处,各纬线圈上相对长度变形ν(见表 1),而长度变形ν随经差或余纬度的变化趋势分别如图 4、5所示。
|
| 图 4 高斯投影长度变形随经差变化规律 Fig. 4 Rules of Length Deformation of Gauss Projection with Longitudes |

|
| 图 5 高斯投影长度变形随余纬度变化规律 Fig. 5 Rules of Length Deformation of Gauss Projection with Latitudes |
由表 1及图 4、5可知,在极区范围内,当点位于中央子午线或极点附近时,变形较小。由于极区复杂的地理环境,该特性可用于沿中央子午线的航线设计。随着远离中央子午线或极点,长度变形渐渐增大。在极圈范围内,长度变形最大值在极圈上经差为90°处,且该值达到了9%,此时已无法满足大比例尺地图的绘制需求,可根据特定用途,用于大洋航行时研究总的航行条件、拟定大洋航线和制定总的航行计划。
| θ | λ=0° | λ=30° | λ=60° | λ=90° |
| 0° | 0 | 0 | 0 | 0 |
| 5° | 0 | 0.001 0 | 0.002 9 | 0.003 8 |
| 10° | 0 | 0.003 8 | 0.011 5 | 0.015 4 |
| 15° | 0 | 0.008 5 | 0.026 1 | 0.035 3 |
| 20° | 0 | 0.015 0 | 0.047 0 | 0.064 2 |
| 23.45° | 0 | 0.020 4 | 0.065 3 | 0.090 0 |
根据文献[5]可知,日晷投影为任意投影,即在某点处各方向上长度变形不等。日晷投影主方向(纬线圈方向及子午线方向)上的长度变形公式为:

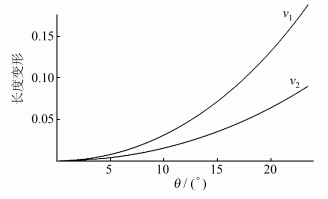
式中,ν1、ν2分别表示纬线圈和子午线方向上的长度变形,其中ν1为日晷投影的极大长度变形,ν2为极小长度变形。将日晷投影平面上某些特殊点处的长度变形值列于表 2,并借助计算机代数系统绘制出长度变形ν1、ν2 随着其远离极点的变化趋势(见图 6)。
| θ | ν1 | ν2 |
| 0° | 0 | 0 |
| 5° | 0.007 7 | 0.003 8 |
| 10° | 0.031 1 | 0.015 4 |
| 15° | 0.071 8 | 0.035 3 |
| 20° | 0.132 5 | 0.064 2 |
| 23.45° | 0.188 2 | 0.090 0 |
|
| 图 6 日晷投影长度变形示意图 Fig. 6 Length Deformation of Gnomonic Projection |
根据式(14),结合表 2及图 6可以看出,随着远离极点,日晷投影的长度变形逐渐增大,且纬线圈方向的长度变形大于子午线方向上的长度变形。将高斯投影长度变形 ν与日晷投影的极小长度变形ν2进行比较,有:
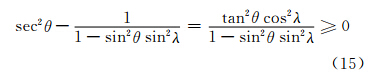
则可得出结论:在极圈范围内,高斯投影长度变形小于日晷投影的极小长度变形,故其面积变形也小于日晷投影。考虑到高斯投影具有保角性质,便于确定方位,可以说,高斯投影在极区更便于应用。
2.3 子午线偏移角
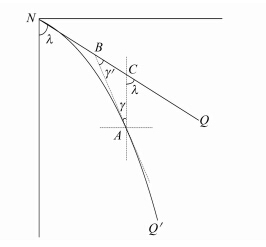
根据球面高斯投影的特性可知,投影平面上的子午线为一组始于极点且收敛于坐标纵轴的曲线,并由图 3可以看出,这组曲线近似为直线。为与日晷投影平面上的子午线进行比较,更直观说明高斯投影子午线的形状,本文提出了偏移角 γ′的概念。考虑到球面高斯投影的对称性,下文对经差λ∈[0,90°]的偏移角公式进行推导。
|
| 图 7 子午线偏移角示意图 Fig. 7 Diagram of Meridian Deviation Angle |
如图 7所示,分别采用高斯投影和日晷投影将极区投影至平面上,NQ′、NQ分别为经差为λ的子午线经高斯投影与日晷投影后的曲线。定义子午线偏移角γ′为NQ′到NQ的夹角,且顺时针方向为正方向。图 7中,辅助线AC为坐标纵线方向,AB为NQ'曲线上点A处的切线。根据子午线收敛角γ的定义及三角形的基本性质,可知∠BAC=γ,∠BAC+∠ABC=∠ACQ,即λ=-γ′+γ,则子午线偏移角为:

又根据文献[7]可知,tanγ= x |λ |/ y |λ |,结合投影公式(6),可得:

将式(17)代入式(16),可得:
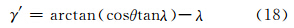
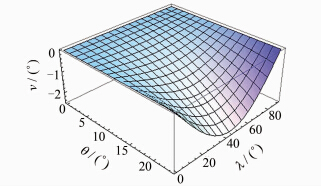
利用计算机代数系统可绘制出极圈内,即 [0≤θ≤23.45°,0≤λ≤90°]范围内γ′的变化趋势,如图 8所示。
|
| 图 8 极区内子午线偏移角变化趋势 Fig. 8 Trend of Meridian Deviation Angle in Polar Region |
从图 8可以看出,在极区范围内,当经差一定时,子午线偏移量 γ′ 随着余纬度θ的增大而加速增大;当余纬度θ保持不变时,γ′ 随着λ的变化趋势为先变大后变小,在经差为 0°以及90°时,偏移角γ′为0°。为了更明确地了解|γ′|值的变化情况,分别取θ为5°、10°、15°、20°、23.45°,可以得出对应纬度圈上|γ′|最大处及最大值(见表 3)。
| θ/(°) | 5 | 10 | 15 | 20 | 23.45 |
| λ/(°) | 45.054 6 | 45.219 3 | 45.496 6 | 45.890 8 | 46.234 4 |
| γ′max/(°) | 0.109 2 | 0.438 6 | 0.993 1 | 1.781 7 | 2.468 8 |
结合图 8,从表 3中可以看出,在余纬度很小时,子午线偏移角很小,即高斯投影的子午线形状接近日晷投影后的子午线形状。也就是说,越接近极点,高斯投影子午线越接近为直线。在极圈范围内,子午线偏移角最大处为极圈上经差为45°附近,该最大值为2.468 8°。在纬度80°以上,子午线偏移角最大值为0.438 6°。
3 结 语
本文以球面高斯投影闭合公式为基础,通过引入余纬度,推导出了适用于极区的非奇异高斯投影公式。根据该公式对投影进行数学分析并与日晷投影进行比较,可得如下结论。
1) 极区非奇异的高斯投影闭合公式解决了传统公式在极区的奇异现象,一定程度上丰富了地图投影数学基础,完善了地图投影理论。
2) 推导出的极区高斯投影经纬线方程,其纬线圈投影方程形如椭圆方程,而子午线方程形如双曲线方程。
3) 将高斯投影与日晷投影公式分别展开成关于余纬度的幂级数,可知在极区当余纬度很小时,这两种投影非常接近。
4) 在极区范围内,高斯投影长度变形小于日晷投影,且高斯投影子午线形状接近日晷投影子午线形状。考虑到高斯投影具有保角性质,可更好地确定方位关系,对于绘制极区沿中央子午线的地形图具有重要参考价值,可结合目前北极航线绘制满足需要的极区航海图。将高斯投影用于极区比日晷投影更有优势。
| [1] | Wang Qinghua, E Dongchen, Chen Chunming, et al. Popular Map Projections in Antarctica and Their Application[J]. Chinese Journal of Polar Research, 2002, 14(3): 226-233 (王清华, 鄂栋臣, 陈春明, 等. 南极地区常用地图投影极其应用[J]. 极地研究, 2002, 14(3): 226-233) |
| [2] | E Dongchen, Liu Yongnuo, Guo Xiaogang. Surveying in Antarctica[J]. Acta Geodaetica et Cartographic Sinica, 1985, 14(4): 305-314 (鄂栋臣, 刘永诺, 国晓港. 南极测绘[J]. 测绘学报, 1985, 14(4): 305-314) |
| [3] | Ye Jing. A Probe into the History, Current Situation and Prospect of Canadian Arctic Disputes[J]. Wuhan University Journal (Humanity Sciences), 2013, 66(2): 115-121 (叶静. 加拿大北极争端的历史、现状与前景[J]. 武汉大学学报 (人文科学版), 2013, 66(2): 115-121) |
| [4] | Ding Jiabo. Ellipsoidal Gnomonic Projection by Double Method[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(2): 183-185 (丁佳波. 采用双重投影法的椭球面日晷投影[J]. 武汉测绘科技大学学报, 2000, 25(2): 183-185) |
| [5] | Liu Qun. The Theory of Gnomonic Projection and its Application[J]. Journal of Guizhou Normal University (Natural Science), 2003, 21(3): 109-112 (刘群. 日晷投影原理及其应用[J]. 贵州师范大学学报(自然科学版), 2003, 21(3): 109-112) |
| [6] | Hua Tang. The Selection of Spherical Radius for Gnomonic Projection on Large and Medium Scale[J]. Acta Geodaetica et Cartographic Sinica, 1984, 13(2): 141-151 (华棠. 大、中比例尺日晷投影图球半径的选择[J]. 测绘学报, 1984, 13(2): 141-151) |
| [7] | Yang Q H, Snyder J P,Tobler W R. Map Projection Transformation: Principles and Applications[M]. London: Taylor&Francis, 2000 |
| [8] | Xiong Jie. Ellipsoidal Geodesy [M]. Beijing: Publishing Housing of PLA, 1988 (熊介. 椭球大地测量学[M]. 北京: 解放军出版社, 1988) |
| [9] | Li Houpu, Bian Shaofeng. The Expression of Gauss Projection by Complex Numbers[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 5-9(李厚朴, 边少锋. 高斯投影的复变函数表示[J]. 测绘学报, 2008, 37(1): 5-9) |
| [10] | Li Houpu, Bian Shaofeng. Expressions for Analytical Transformation Between Gauss and Mercator Projections by Complex Numbers[J]. Geomatics and Information Science of Wuhan University, 2009, 34(3): 277-279 (李厚朴, 边少锋. 高斯投影与墨卡托投影解析变换的复变函数表达式[J]. 武汉大学学报·信息科学版, 2009, 34(3): 277-279) |
| [11] | Li Zhongmei, Yu Jinxing, Li Houpu, et al. The Verification of Equivalence Between Gauss and Transverse Mercator Projecitons[J]. Hydrographic Surveying and Charting, 2013, 33(3): 17-20 (李忠美, 于金星, 李厚朴, 等. 高斯投影与高斯投影等价性证明[J]. 海洋测绘, 2013, 33(3): 17-20) |
| [12] | Bian Shaofeng, Li Houpu. Mathematical Analysis in Cartography by Means of Computer Algebra System[C]//Bateira C. Cartography-A Tool for Spatial Analysis. Croatia: Intech, 2012 |
 2015, Vol. 40
2015, Vol. 40



