文章信息
- 田晶, 王一恒, 颜芬, 熊富全
- TIAN Jing, WANG Yiheng, YAN Fen, XIONG Fuquan
- 一种网络空间现象同位模式挖掘的新方法
- A New Method for Mining Co-location Patterns Between Network Spatial Phenomena
- 武汉大学学报·信息科学版, 2015, 40(5): 652-660
- Geomatics and Information Science of Wuhan University, 2015, 40(5): 652-660
- http://dx.doi.org/10.13203/j.whugis20130448
-
文章历史
- 收稿日期:2013-08-29
2. 武汉大学地理信息系统教育部重点实验室, 湖北 武汉, 430079
2. Key Laboratory of Geographic Information System, Ministry of Education, Wuhan University, Wuhan 430079, China
现实世界中,很多与人相关的现象和事件邻近、沿着或发生于交通网络,如交通事故、街头犯罪、基础设施的分布等,这些现象被称为网络空间现象,几何上可抽象表达为网络上或邻近网络的点[1, 2]。网络空间分析是空间分析领域的热门研究问题与重要的研究议题[2, 3]。网络空间分析的显著特点是其距离测度由平面上的欧氏距离变为网络上的最短路径距离,整个平面由连续变为离散,由同质变为异质。对于城市区域,两点之间的欧氏距离与其网络上的最短路径距离具有显著区别,将平面欧氏空间的一些方法直接应用于网络空间现象的分析时存在一定的缺陷,往往导致错误的结论[4, 5]。对网络空间现象进行分析的一种主要途径是将欧氏空间的经典方法扩展到网络空间,例如网络K函数与网络核函数[1, 6, 7]。
同位模式是频繁出现在同一区域的一组空间要素或事件,它表示布尔空间要素子集,这些子集的实例频繁地同时出现于地理邻近区域[8, 9]。例如,生态学中的尼罗鳄与埃及燕鸻,经济学中的供应商与制造商的分布均是典型的同位模式[10]。同位模式的挖掘是从含有大量布尔要素的空间数据集中检测同位模式,该研究是空间数据挖掘领域感兴趣的课题,同时也是一项重要的数据挖掘任务[9, 11, 12],有助于揭示现象或事件的分布规律,辅助决策支持。同位模式挖掘的方法主要分为空间统计方法和数据挖掘方法两类[8]。空间统计方法运用空间相关性指标来描述不同类型空间要素间的关系,这些指标包括交叉K函数、平均最近邻距离、空间回归模型、可用于度量点和面关联模式的指标、同位系数、Q统计等[13, 14, 15, 16, 17]。数据挖掘方法主要通过选择同位模型来产生事务,然后设计类似于Apriori算法的算法去挖掘同位模式[8],模式是否频繁由参与率和条件概率决定,文献[18, 19, 20, 21]是此类方法的代表。目前有参考要素中心模型、窗口中心模型和事件中心模型三种主要的同位模型[21]。参考要素中心模型[19]聚焦于挖掘特定类型的要素与其他类型的要素的同位模式,该模型通过定义邻近关系产生事务; 窗口中心模型又称为划分模型,它首先定义合适大小的窗口,然后将所有窗口作为事务产生的依据; 事件中心模型[8]常用于找出所有可能同位的空间要素子集,与参考要素中心模型一样需要定义邻居关系来产生事务。目前,对于网络空间现象同位模式挖掘的研究较少,这是本文研究关注的问题。网络空间现象关联模式挖掘的方法主要有网络交叉K函数、网络交叉最近邻距离等[1]。
文献[22]提出了一种同位模式挖掘方法,该方法的理论基础源于自然语言理解,其基本思想是建立同位模型提取处于同现关系的布尔要素子集,设计统计量判断不同布尔要素类间的统计独立性来确定同现关系是否具有统计显著性。该方法在建立同位模型时,是通过网格对平面进行划分,属于同一网格内的点对即为同现,同时,该文也提到可以定义其他同位模型描述同现关系。本文将该方法扩展至网络空间,通过对道路网络进行划分来确定哪些要素类具有同现关系,判断不同要素类间的统计独立性来确定该同现关系是否频繁到从统计意义上构成同位模式,并将该方法应用于集聚经济学中不同产业的公司之间的同位模式挖掘。
1 方 法
本文方法包括两个核心步骤:第一,通过对道路网络的划分来建立网络空间现象同位模型,用于确定不同要素类间是否存在同现关系;第二,基于要素类间的同现关系,从要素类间的统计独立性出发设计统计指标,判定某一同现关系是否频繁到构成具有统计显著性的同位模式。
1.1 同位模型的建立
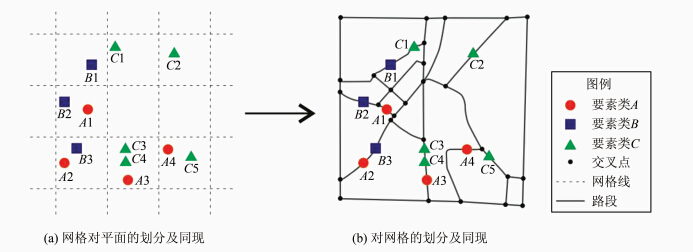
文献[22]使用均匀的网格对整个平面进行划分,将不同要素类的实例出现在同一网格内定义为同现,将该实例定义为同现实例,在一个网格内只考虑实例出现与否而不考虑实例出现的次数。如图 1(a),要素类 A,B和C的同现实例有{A1,B2}、{A2,B3}、{A3,C3,C4}和{A4,C5}。A3、C3和C4在同一个网格内,为一个同现实例。
本文通过对道路网络的划分实现对平面的划分。对于一个道路网络L,如图 1(b),对其进行划分,使得L={l1,l2,…,ln}为平图 ,即路段仅在端点处相交的图。如果要素类B和要素类C的实例同时出现在某一路段li上,则定义要素类B和要素类C间有同现,且定义该实例为同现实例,本文不考虑要素类B或C的实例出现的次数,仅考虑其是否出现。如图 1(b),网络 L被划分为多条路段,同现实例有{B1,C1}、{A2,B3}和{A3,C3,C4}。A3、C3和C4在同一个路段上,为一个同现实例。
网络划分形成的同现和网格划分形成的同现存在区别。A1和B2在同一个网格内,但在不同路段上,故在欧氏空间是A和B的同现实例,在网络空间不是A和B的同现实例。A4和C5在同一网格内,但在不同路段上,故在欧氏空间是A和C的同现实例,在网络空间不是A和C的同现实例。B1和C1在不同网格内,但在同一路段上,故在网格空间不是B和C的同现实例,在网络空间是B和C的同现实例。
|
| 图 1 网格划分与网络划分示意图 Fig. 1 Grid Partition and Network Partition |
当然,对网络的划分不限于本文的定义,可按照等长对各路段进行划分,例如文献[7]在对交通事故的热点进行分析时,对道路采用定长划分,称之为“线素”。然而,定长划分在长度的选择以及怎样为一条线段的问题上存在较大的不确定性。如图 1(b),是对l1、l4和l7共同构成一条线段后再等长划分,还是对l1、l4和l7各自等长划分呢?也可按照对网络进行区块划分,每个区块中道路的总长度相等[23],然而,该方法由于起始点的不同,生成的分区也是不确定的。采用本文提出的模型具有划分的唯一性,缺点是由于道路网结构模式的不同,导致路段长度可能出现较大的不均匀性。 1.2 同现关系的统计推断
同位模型建立后,通过统计推断来确定要素类X和要素类Y是否独立,从而确定两个要素类对应的同现是否频繁到从统计意义上构成同位模式。
令P(X,Y)表示要素类X和要素类Y同现的概率,N为网络中线段的总数,Nxy表示网络中要素类X和要素类Y同现的线段总数,则X和Y同现的概率P(X,Y)的估计值为:
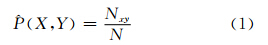
要素类Y出现的情况下,X出现的概率为P(X |Y),其估计值为:
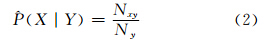
其中,Ny表示要素类Y的实例出现的线段总数。
令Sx表示X以概率P(X)在Ny段上出现的数量,Sx|y表示X以概率P(X | Y)在Ny段上出现的数量。下文确定Sx和Sx|y在统计上是否不同。如果Sx和Sx|y相差很大,就表明在一个高置信水平下分布不同。
对于如何度量Sx和Sx|y的偏差,注意到式(1)中的涉及要素类X和Y出现和不出现,并不关心在同一线段上X和Y出现的个数,所以Sx是二项分布随机变量,其数学期望为NyP(X),方差为NyP(X)(1-P(X))。由此,Sx的数学期望E(Sx)的估计值以及Sx的标准差σSx的估计值为:
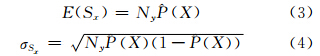
Sx|y的数学期望E(Sx|y)的估计值为:
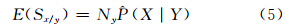
随后,可以进行二项分布检验去度量Y对X分布的影响:
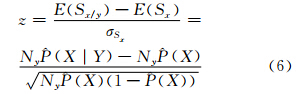
除了在样本量非常小的情况下,由中心极限定理可知,二项分布近似于正态分布。则当z>1.96时,说明在95%的置信水平下要素类X和Y同现的概率远大于当X和Y的分布独立时同现的期望值,即要素类X和Y同现是频繁的,它们从统计意义上构成同位模式。当z<-1.96时,说明在95%的置信水平下要素类X和Y同现的概率远小于当要素类X和Y的分布独立时同现的期望值,即从统计意义上要素类X和Y相互排斥。 2 案例研究
为了说明本文提出的网络空间现象同位模式挖掘方法如何应用及其有效性,本文将该方法应用于集聚经济学中不同行业公司的分布模式研究,判断制造业对应的二位数行业中哪些行业的公司分布具有同位模式。同时,将文献[22]的方法与本文方法进行比较,并运用网络交叉K函数对他们的差别进行验证。
深圳市的通信设备、计算机及其他电子设备制造行业在全国范围内处于领先地位,化学原料及化学制品制造业、金属制造业、交通运输设备制造业和电气机械及器材制造业等4个行业在广东省处于领先地位,纺织业、纺织服装、鞋帽制造业、家具制造业等劳动力密集型行业仍吸引着众多劳动力[24],对深圳市制造业公司分布规律的研究具有一定意义,为这些公司的区位选择提供了一定的支持。
2.1 数据及其预处理
深圳市制造业公司的数据由中国广东省深圳市基础地理信息中心提供,为2009年的深圳市兴趣点数据子集。由于该数据较为粗糙,所以进行了一定的预处理。依据《国民经济行业分类与代码GB/T 4754-2002》[25],根据公司的业务范围与主营产品将公司进行归类,对于信息不全的公司,通过电话咨询以及上网搜索等方式将信息补齐,共50 806个公司,见表 1。
| 行业分类及名称 | 数量 | 行业分类及名称 | 数量 |
| C13农副食品加工业 | 132 | C29橡胶制品业 | 77 |
| C14食品制造业 | 57 | C30塑料制品业 | 2 209 |
| C15饮料制造业 | 131 | C31非金属矿物制品业 | 641 |
| C16烟草制造业 | 8 | C32黑色金属冶炼及压延加工业 | 43 |
| C17纺织业 | 138 | C33有色金属冶炼及压延加工业 | 17 |
| C18纺织服装、鞋帽制造业 | 2 933 | C34金属制造业 | 3 291 |
| C19皮革、毛皮、羽毛(绒)及其制品业 | 774 | C35通用设备制造业 | 346 |
| C20木材加工及木、竹、藤、棕、草制品业 | 507 | C36专用设备制造业 | 3 656 |
| C21家具制造业 | 847 | C37交通运输设备制造业 | 326 |
| C22造纸及纸制品业 | 1 113 | C39电气机械及器材制造业 | 1 653 |
| C23印刷业及记录媒介的复制 | 1 877 | C40通信设备、计算机及其他电子设备制造 | 18 550 |
| C24文教体育用品制造业 | 824 | C41仪器仪表及文化、办公用机械制造业 | 514 |
| C26化学原料及化学制品制造业 | 1 710 | C42工艺品及其他制造业 | 7 981 |
| C27医药制造业 | 451 |
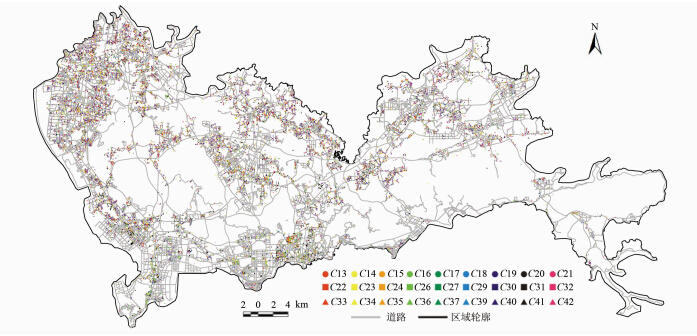
道路网数据为深圳市1∶10 000道路网数据,对其进行必要的预处理,删除立交桥,对道路网进行拓扑检查,删除伪结点,并在交叉点处打断,对道路网络进行划分,处理后路段数量为N=14 822,深圳市制造业公司的分布与相应的道路网见图 2。
|
| 图 2 深圳市道路网以及制造业公司的分布 Fig. 2 Road Network and Distribution of Manufacturing Firms in Shenzhen City |
从表 2的实验结果可知,351个行业对中有309对行业呈现统计意义下(95%置信度)的同位模式,42对行业的分布模式既不同位也不排斥,无行业对的分布模式为排斥分布。其中,文教体育用品制造业 (C24)、化学原料及化学制品制造业(C26)、专用设备制造业(C36)、电气机械及器材制造业(C39)、通信设备、计算机及其他电子设备制造(C40)和工艺品及其他制造业(C42)等6个行业可与除本行业以外的制造业行业形成同位模式,木材加工及木、竹、藤、棕、草制品业(C20)、家具制造业(C21)、造纸及纸制品业(C22)、塑料制品业(C30)、非金属矿物制品业(C31)和金属制造业(C34)等6个行业可与除本行业和烟草制造业(C16)之外的制造业行业分别形成同位模式。
| C13 | C14 | C15 | C16 | C17 | C18 | C19 | C20 | … | C32 | C33 | C34 | C35 | C36 | C37 | C39 | C40 | C41 | C42 | |
| C13 | 6.85 | 7.73 | -0.24 | 1.01 | 8.31 | 2.47 | 6.63 | … | -0.56 | -0.34 | 6.78 | 6.25 | 5.97 | 4.01 | 5.37 | 5.18 | 1.55 | 8.25 | |
| C14 | 6.83 | 7.20 | -0.16 | 3.69 | 5.46 | 1.87 | 2.28 | … | -0.38 | -0.23 | 6.54 | 6.10 | 7.47 | 3.95 | 6.50 | 6.17 | 5.24 | 6.99 | |
| C15 | 7.73 | 7.21 | -0.23 | 6.40 | 19.08 | 9.09 | 3.35 | … | 1.35 | -0.32 | 9.04 | 16.16 | 14.71 | 12.90 | 17.77 | 14.87 | 6.46 | 16.16 | |
| C16 | -0.24 | -0.16 | -0.23 | -0.24 | 1.77 | 1.37 | -0.41 | … | -0.14 | -0.08 | 0.09 | -0.35 | 3.30 | -0.36 | 3.53 | 2.18 | -0.44 | 2.83 | |
| C17 | 1.01 | 3.69 | 6.41 | -0.24 | 16.08 | 8.60 | 2.30 | … | 4.68 | -0.35 | 9.09 | 6.67 | 10.12 | 5.14 | 8.40 | 11.95 | 9.56 | 9.61 | |
| C18 | 8.67 | 5.71 | 19.90 | 1.85 | 16.76 | 27.64 | 13.74 | … | 2.59 | 3.56 | 30.21 | 25.31 | 35.91 | 17.27 | 32.94 | 37.82 | 25.02 | 38.34 | |
| C19 | 2.51 | 1.91 | 9.24 | 1.40 | 8.74 | 26.94 | 9.17 | … | 5.30 | 1.98 | 23.29 | 10.11 | 20.98 | 7.59 | 18.40 | 22.26 | 19.86 | 21.11 | |
| C20 | 6.69 | 2.30 | 3.38 | -0.42 | 2.32 | 13.29 | 9.09 | … | 3.19 | 2.89 | 16.58 | 4.75 | 14.20 | 6.14 | 13.66 | 11.76 | 8.16 | 16.30 | |
 |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  | |
| C32 | -0.56 | -0.38 | 1.34 | -0.14 | 4.66 | 2.48 | 5.20 | 3.15 | … | 5.02 | 8.81 | 2.81 | 7.67 | 1.53 | 5.51 | 8.61 | 5.76 | 6.16 | |
| C33 | -0.33 | -0.23 | -0.32 | -0.08 | -0.34 | 3.40 | 1.94 | 2.86 | … | 5.02 | 5.30 | -0.49 | 4.67 | 1.48 | 3.99 | 4.27 | 1.00 | 4.69 | |
| C34 | 7.24 | 7.00 | 9.66 | 0.09 | 9.71 | 30.95 | 24.49 | 17.57 | … | 9.44 | 5.68 | 16.96 | 39.74 | 13.83 | 31.74 | 35.78 | 21.94 | 35.53 | |
| C35 | 6.28 | 6.14 | 16.24 | -0.35 | 6.70 | 24.39 | 10.00 | 4.74 | … | 2.83 | -0.50 | 15.95 | 23.77 | 15.92 | 23.05 | 18.80 | 14.38 | 20.72 | |
| C36 | 6.36 | 7.98 | 15.69 | 3.53 | 10.78 | 36.71 | 22.00 | 15.01 | … | 8.20 | 4.99 | 39.65 | 25.22 | 18.78 | 39.37 | 43.00 | 20.98 | 39.21 | |
| C37 | 4.03 | 3.98 | 12.98 | -0.36 | 5.17 | 16.65 | 7.50 | 6.12 | … | 1.54 | 1.49 | 13.01 | 15.93 | 17.71 | 17.36 | 16.88 | 5.80 | 16.90 | |
| C39 | 5.55 | 6.73 | 18.38 | 3.66 | 8.69 | 32.66 | 18.71 | 14.01 | … | 5.72 | 4.14 | 30.71 | 23.72 | 38.18 | 17.85 | 39.17 | 18.88 | 33.49 | |
| C40 | 5.78 | 6.89 | 16.59 | 2.44 | 13.32 | 40.43 | 24.42 | 13.00 | … | 9.63 | 4.78 | 37.33 | 20.85 | 44.97 | 18.72 | 42.25 | 23.06 | 45.40 | |
| C41 | 1.57 | 5.30 | 6.52 | -0.44 | 9.65 | 24.23 | 19.74 | 8.18 | … | 5.83 | 1.01 | 20.74 | 14.45 | 19.88 | 5.83 | 18.44 | 20.89 | 19.70 | |
| C42 | 8.93 | 7.58 | 17.50 | 3.07 | 10.40 | 39.80 | 22.48 | 17.50 | … | 6.68 | 5.09 | 35.99 | 22.32 | 39.81 | 18.20 | 35.06 | 44.07 | 21.11 | |
| 注: 表格第一行和第一列分别为行业代码Ci和Cj(13≤i,j≤42,且i,j不为25、28和38),其余单元格内数字表示Ci对Cj(i≠j)的影响z值。 | |||||||||||||||||||
根据集聚经济学理论中产生集聚现象的三个重要机制对结果进行定性分析。这三个重要机制是劳动力集聚、知识溢出和行业间的前后向联系[26]。这些机制与同位模式是相互促进、相互影响的关系,而且,这些机制并不是孤立的,某种同位模式可能与这三种机制都有关联。所以,本文以其主要作用的机制作为分析依据。
1) 劳动力集聚。劳动力通过转移集聚在某一特定区域,形成劳动力市场,从而产生集聚效应,集聚效应能够促进行业间劳动力的流动和共享,有利于降低企业的劳动力成本(如培训费等)和降低工人失业率[26]。行业内企业会集聚分布,但会出现同行产品竞争力过强等不利于企业发展的现象。因此,为了获得更大的劳动力集聚效应,且尽量降低不利因素的影响,企业会靠近能够共享劳动力的其他行业的企业,从而促成了行业间同位模式的形成。同位模式形成后,地理上的邻近性又给企业带来更多共享劳动力的机会,增强了劳动力集聚效应。由于劳动力密集型行业更需要共享劳动力,劳动力更易在拥有相似技术或者技术含量较低的岗位间流动,因此,典型的劳动力密集型行业之间易形成同位模式。在本文研究中,纺织服装、鞋帽制造业(C18)和皮革、毛皮、羽毛(绒)及其制品业(C19)需要大量的劳动力,且对劳动力的技术要求较低,二者之间有着较明显的共享劳动力现象,橡胶制品业(C29)和塑料制品业(C30)的岗位相似度较高[27],岗位相似度越高意味着劳动力流动更频繁,共享程度更高。有着受益于劳动力集聚效应的驱动力,这就不难理解纺织服装、鞋帽制造业(C18)和皮革、毛皮、羽毛(绒)及其制品业(C19)、橡胶制品业(C29)和塑料制品业(C30)形成同位模式。
2) 知识溢出。通过员工流动、公司交流学习等方式促进行业间知识共享,有利于增大行业的知识储量。对于可以通过产品、语言文字等方式溢出的显性知识和难规范、高度个人化只能通过面对面交流的方式进行传播的隐性知识来说,知识溢出更主要的是促进隐性知识的传播和扩散。隐性知识的溢出一定程度上受到地理距离和行业之间知识或者技术的相似程度的限制[28],因此,行业间形成同位模式以获得更大的知识溢出。那些从知识溢出受益较多的行业对知识溢出的需求 大,易形成同位模式。在本文研究中,化学原料及化学制品制造业( C26)和医药制造业(C27)同属于化学工业,生产相关化学制品的技术、工艺和经验等知识的溢出能促进知识的取长补短,增加行业的知识容量。电力电子元器件制造属于电气机械及器材制造业(C39),光电子器件及其他电子器件制造属于通信设备、计算机及其他电子设备制造业(C40),对电子器件的设计、改进等知识的溢出能提高电气机械及器材制造业(C39)和通信设备、计算机及其他电子设备制造业(C40)这两个行业的知识水平,从而提高行业的创新开发能力。有着受益于知识溢出的驱动力,这就不难理解化学原料及化学制品制造业(C26)和医药制造业(C27)、电气机械及器材制造业(C39)和通信设备、计算机及其他电子设备制造业(C40)形成 同位模式。
3) 前后向关联。具有前向联系或后向联系的两个行业为了减少中间投入品的运输成本和在途损耗[24],一个行业的企业会选择邻近另一行业的企业的产址,因此形成同位模式。如文献[29]提到的橡胶和机动车,橡胶制品业(C29)依赖于橡胶原料,机动车制造属于交通运输设备制造业(C37),二者形成同位模式在于橡胶制品业可为机动车的制造提供橡胶制品,如轮胎。有前后向联系的行业易形成同位模式,特别是在制造中间产品的行业和制造最终需求产品的行业之间,在本文研究中,木材加工及木、竹、藤、棕、草制品业(C20)向家具制造业(C21)提供加工木材等中间产品,金属制品业(C34)向通用设备制造业(C35)和专用设备制造业(C36)提供金属制品等中间产品。要知道,运输木材、金属制品等中间产品需要耗费一定的人力、物力、财力和时间,还可能因为意外而损失产品,有着减少开支和降低损失的驱动力,这就不难理解木材加工及木、竹、藤、棕、草制品业(C20)和家具制造业(C21)、金属制品业(C34)和通用设备制造业(C35)、金属制品业(C34)和专用设备制造业(C36)形 成同位模式。
由上述分析可知,运用集聚经济学中的理论可以合理解释得到的同位模式。下文将通过与文献[20]方法的比较来说明本文方法的有效性。 2.3 比 较
为了说明本文方法的有效性,将本文方法与文献[22]的方法同时应用于网络空间现象的同位模式挖掘,找出差别,并使用网络交叉K函数这一网络空间现象同位模式挖掘的常用方法对差别进行验证。
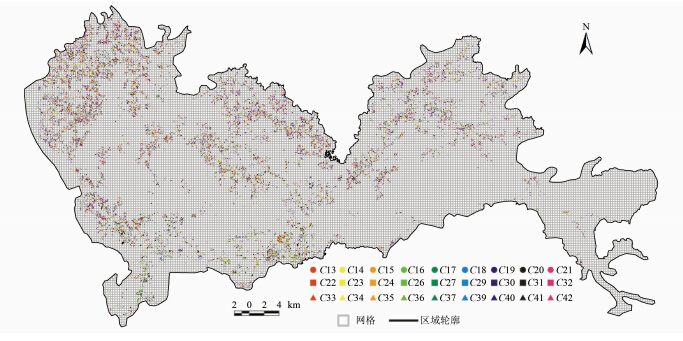
根据文献[22]的方法,运用规则网格对深圳市进行划分。网格分辨率的选择是该方法的关键问题之一,根据文献[22]的建议,网格分辨率既不能太小也不能太大,在选定分辨率下的网格数应大于被分析点集中点数的最大值(本文案例中为18 550)。为了进行比较,选择大于18 550且与路段数相近似的网格数,其对应分辨率为309 m×309 m,对应的网格数为18 607(见图 3)。在同一网格出现的数据点即为同现,统计推断如§2.2节所述,结果见表 3。351个行业对中有312对行业呈现统计意义下(95%置信度)的同位模式,39对行业的分布模式既不同位也不排斥,无行业对的分布模式为排斥分布。
|
| 图 3 深圳市制造业公司的分布的网格划分 Fig. 3 Grid Partition of Manufacturing Firms in Shenzhen City |
| C13 | C14 | C15 | C16 | C17 | C18 | C19 | C20 | … | C32 | C33 | C34 | C35 | C36 | C37 | C39 | C40 | C41 | C42 | ||
| C13 | 8.74 | 10.99 | -0.23 | 1.37 | 9.95 | 4.62 | 5.42 | … | -0.54 | -0.33 | 11.88 | 10.10 | 10.39 | 9.76 | 9.20 | 10.84 | 0.97 | 11.84 | ||
| C14 | 8.72 | 11.15 | 6.05 | 6.87 | 6.82 | 1.65 | 3.40 | … | -0.38 | -0.23 | 8.24 | 6.63 | 6.74 | 8.50 | 5.98 | 9.00 | 8.44 | 7.82 | ||
| C15 | 10.98 | 11.17 | 4.50 | 12.83 | 23.60 | 9.63 | 3.32 | … | 1.52 | -0.30 | 13.28 | 24.14 | 18.84 | 21.04 | 21.23 | 19.72 | 10.37 | 19.57 | ||
| C16 | -0.23 | 6.04 | 4.48 | -0.24 | 3.63 | 1.54 | -0.40 | … | -0.13 | -0.08 | 1.43 | 1.69 | 4.00 | -0.34 | 5.58 | 4.16 | -0.41 | 4.67 | ||
| C17 | 1.37 | 6.89 | 12.84 | -0.24 | 23.82 | 13.66 | 6.36 | … | 6.72 | 1.66 | 17.12 | 11.87 | 18.63 | 7.90 | 15.15 | 18.70 | 12.56 | 15.79 | ||
| C18 | 10.27 | 7.05 | 24.38 | 3.76 | 24.58 | 39.71 | 16.32 | … | 6.66 | 4.27 | 47.71 | 32.73 | 55.85 | 23.54 | 44.53 | 57.99 | 33.02 | 53.69 | ||
| C19 | 4.69 | 1.71 | 9.77 | 1.60 | 13.85 | 39.01 | 9.93 | … | 6.75 | 2.19 | 36.59 | 19.91 | 34.48 | 12.62 | 26.68 | 36.35 | 24.89 | 33.34 | ||
| C20 | 5.46 | 3.43 | 3.34 | -0.40 | 6.40 | 15.93 | 9.87 | … | 6.74 | 4.85 | 23.66 | 8.34 | 21.90 | 8.42 | 14.73 | 20.63 | 12.19 | 22.34 | ||
 |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  | ||
| C32 | -0.53 | -0.38 | 1.52 | -0.13 | 6.70 | 6.44 | 6.64 | 6.67 | … | -0.19 | 10.82 | 2.02 | 8.97 | 1.73 | 4.52 | 10.07 | 5.33 | 7.95 | ||
| C33 | -0.32 | -0.23 | -0.30 | -0.08 | 1.65 | 4.12 | 2.15 | 4.80 | … | -0.19 | 6.90 | 1.67 | 5.66 | 1.60 | 5.70 | 5.88 | 1.15 | 5.81 | ||
| C34 | 12.53 | 8.71 | 14.01 | 1.51 | 18.05 | 48.75 | 38.05 | 24.77 | … | 11.44 | 7.31 | 24.94 | 62.21 | 20.68 | 47.34 | 65.16 | 32.18 | 57.96 | ||
| C35 | 10.14 | 6.67 | 24.25 | 1.71 | 11.92 | 31.83 | 19.71 | 8.31 | … | 2.04 | 1.68 | 23.74 | 31.98 | 23.76 | 28.43 | 28.83 | 19.40 | 30.05 | ||
| C36 | 10.90 | 7.08 | 19.77 | 4.21 | 19.53 | 56.75 | 35.66 | 22.80 | … | 9.43 | 5.96 | 61.86 | 33.41 | 28.15 | 55.00 | 72.06 | 32.83 | 62.35 | ||
| C37 | 9.80 | 8.56 | 21.14 | -0.34 | 7.93 | 22.90 | 12.50 | 8.40 | … | 1.75 | 1.61 | 19.70 | 23.77 | 26.96 | 25.88 | 28.11 | 13.35 | 24.99 | ||
| C39 | 9.45 | 6.16 | 21.81 | 5.76 | 15.56 | 44.30 | 27.02 | 15.01 | … | 4.65 | 5.87 | 46.09 | 29.07 | 53.85 | 26.46 | 58.33 | 25.20 | 48.27 | ||
| C40 | 11.62 | 9.66 | 21.15 | 4.47 | 20.03 | 60.19 | 38.41 | 21.94 | … | 10.82 | 6.32 | 66.20 | 30.77 | 73.62 | 29.98 | 60.87 | 35.54 | 71.44 | ||
| C41 | 1.03 | 8.52 | 10.46 | -0.42 | 12.66 | 32.25 | 24.75 | 12.20 | … | 5.39 | 1.16 | 30.76 | 19.48 | 31.56 | 13.40 | 24.75 | 33.44 | 30.63 | ||
| C42 | 12.54 | 8.30 | 20.74 | 4.96 | 16.72 | 55.09 | 34.82 | 23.48 | … | 8.44 | 6.18 | 58.20 | 31.70 | 62.96 | 26.34 | 49.78 | 70.61 | 32.17 | 32.17 | |
| 注: 表格第一行和第一列分别为行业代码Ci和Cj(13≤i,j≤42,且i,j不为25、28和38),其余单元格内数字表示Ci对Cj(i≠j)的影响z值。 | ||||||||||||||||||||
使用文献[22]的方法得到的结果与使用本文方法得到的结果的差别表现为:6个行业对在使用文献[20]的方法时为同位模式,但在使用本文方法时不为同位模式,它们是 {C13,C29}、{C14,C16}、{C14,C29}、{C15,C16}、{C16,C18}和{C19,C33};3个行业对在使用本文方法时为同位模式,但在使用文献[22]的方法时不为同位模式,它们是{C29,C32}、{C29,C33}和{C32,C33}。
网络交叉K函数通过检验两个点集在网络上的分布是否相互影响及影响程度,来判断点集间的聚集或者排斥,该方法是检验网络空间现象同位模式的常用方法[1, 8]。图 4展示了某一要素类A对另一要素类B的分布的影响的结果,蓝色曲线表示实际的观察值,红色曲线表示完全空间随机假设情况下的平均值,绿色曲线与粉红色曲线分别表示完全空间随机假设情况下的上界与下界。图 4表示在0~10 000 m的范围内,观察值大于上界,可知要素类B趋向于要素类A集聚;在10 000~20 000 m的范围内,观察值小于上界且大于下界,可知要素类B既不趋向于要素类A集聚,也不排斥要素类A。使用SANET 4.0 工具以95%的置信度对上文中具有差别的9个行业对进行检验。
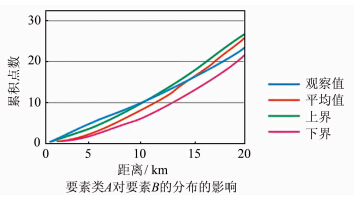
|
| 图 4 网络交叉K函数计算结果示意图 Fig. 4 Illustration of Computing Results of Network Cross K-function |
在使用文献[22]的方法时为同位模式,但在使用本文方法时不为同位模式的6个行业对,在网络交叉K函数的检验下均是既不集聚也不排斥的,符合运用本文方法所得的结果,即不构成同位模式。以行业对{C16,C18}为例,检验结果见图 5,图 5(a)中,C18既不趋向于C16集聚,也不排斥C16;图 5(b) 中,C16既不趋向于C18集聚,也不排斥C18;在使用本文方法时为同位模式,但在使用文献[22]方法时不为同位模式的3个行业对,在网络交叉K函数的检验下均是集聚的,即形成同位模式。以行业对{C29,C32}为例,检验结果见图 6,图 6(a)中,C32趋向于C29集聚;图 6(b) 中,C29趋向于C32集聚。经过验证,网络交叉K函数与本文方法得到了一致的结果。由此可知,本文方法在应用于网络空间现象的同位模式挖掘上优于文献[22]的方法,表明本文将欧氏空间方法扩展至网络空间是有效的。
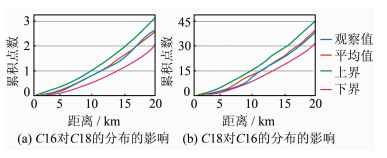
|
| 图 5 网络交叉K函数对行业对 C16和C18的检验 Fig. 5 Test of Relationship Between C16 and C18 Using Network Cross K-function |
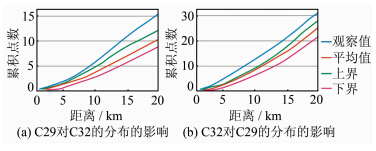
|
| 图 6 网络交叉K函数对行业对C29和 C32的检验 Fig. 6 Test of Relationship Between C29 and C32 Using Network Cross K-function |
本文对文献[22]的方法进行了扩展,通过划分网络来确定要素类间是否存在同现关系,进而通过设计统计指标来判断这些同现关系是否频繁到从统计意义上构成同位模式。对深圳市制造业公司同位模式的挖掘验证了本文方法,与文献[22]的比较说明了本文方法的有效性。目前,地理信息科学处于大数据背景与云计算环境下,数据获取与复杂计算的困难已得到基本改善。下一步的研究拟收集经济学领域的统计数据,如公司的雇佣人员、人数不同产业间供应关系以及生产某产品的核心技术的相似性等专题数据,以对本文得出的同位模式进行经济学的定量验证。同时,在本文方法的原理上进行扩展,该方法目前只能判断要素类两两之间是否构成同位模式,即二项集,下一步研究应扩展到n项集的判断。
| [1] | Okabe A, Yamada I. The K-Function Method on a Network and Its Computational Implementation [J]. Geographical Analysis, 2001, 33(3): 271-290 |
| [2] | Okabe A, Okunuki K, Shiode S. SANET: A Toolbox for Spatial Analysis on a Network [J]. Geographical Analysis, 2006, 38(1): 57-66 |
| [3] | Batty M. Network Geography: Relations, Interactions, Scaling and Spatial Processes in GIS[M]//Unwin D, Fisher P. Re-presenting Geographical Information Systems. Chichester: John Wiley and Sons, 2005 |
| [4] | Yamada I,Thill J. Comparison of Planar and Network K-Functions in Traffic Accident Analysis[J]. Journal of Transport Geography, 2004, 12(2): 149-158 |
| [5] | Lu Yongmei, Chen Xuwei. On the False Alarm of Planar K-Function when Analyzing Urban Crime Distributed Along Streets[J]. Social Science Research, 2007, 36(2): 611-632 |
| [6] | Borruso G. Network Density Estimation: A GIS Approach for Analysing Point Patterns in a Network Space [J]. Transactions in GIS, 2008, 12(3): 377-402 |
| [7] | Xie Zhixiao, Yan Jun. Kernel Density Estimation of Traffic Accidents in a Network Space [J]. Computers, Environment and Urban Systems, 2008, 32(5):396-406 |
| [8] | Huang Yan,Shekhar S, Xiong Hui. Discovering Co-location Patterns from Spatial Data Sets: A General Approach [J]. IEEE Transactions on Knowledge and Data Engineering, 2004, 16(12): 1 472-1 485 |
| [9] | Huang Yan, Pei Jian, Xiong Hui. Mining Co-location Patterns With Rare Events from Spatial Data Sets [J]. Geoinformatica, 2006, 10(2): 239-260 |
| [10] | Hu Wei. Co-Location Pattern Discovery [C]. Encyclopedia of GIS [C]. Berlin: Springer-Verlag, 2008 |
| [11] | Li Deren, Li Deyi, Wang Shuliang. Spatial Data Mining Theories and Applications [M]. Beijing: Science Press, 2006(李德仁, 李德毅, 王树良. 空间数据挖掘理论与应用 [M]. 北京: 科学出版社, 2006) |
| [12] | Li Deren, Wang Shuliang, Shi Wenzhong, et al. On Spatial Data Mining and Knowledge Discovery (SDMKD)[J]. Geomatics and information science of Wuhan University, 2001,26(6):491-499. (李德仁,王树良,史文中,等. 论空间数据挖掘和知识发现[J]. 武汉大学学报·信息科学版,2001,26(6):491-499) |
| [13] | Arnia G, Espa G, Quah D. A Class of Spatial Econometric Methods in the Empirical Analysis of Clusters of Firms in the Space [J]. Empirical Economics, 2008, 34(1): 81-103 |
| [14] | Ruiz M, Lopez F, Paez A. Testing for Spatial Association of Qualitative Data Using Symbolic Dynamics [J]. Journal of Geographical Systems, 2010, 12(3): 281-309 |
| [15] | Leslie T F, Kronenfeld B J. The Co-location Quotient: A New Measure of Spatial Association between Categorical Subsets of Points [J]. Geographical Analysis, 2011, 43(3): 306-326 |
| [16] | Guo Luo, Du Shihong, Haining R, et al. Global and Local Indicator of Spatial Association Between Points and Polygons: A Study of and Use Change [J]. International Journal of Applied Earth Observation and Geoinformation, 2013, 21:384-396 |
| [17] | Bian Fuling, Wan You. A Novel Spatial Co-location Pattern Mining Algorithm Based on k-Nearest Feature Relationship[J]. Geomatics and Information Science of Wuhan University,2009, 34(3):331-334(边馥苓,万幼. k-邻近空间关系下的空间同位模式挖掘算法[J]. 武汉大学学报·信息科学版,2009,34(3):331-334) |
| [18] | Koperski K, Han Jawei. Discovery of Spatial Association Rules in Geographic Information Databases [C]. The 4th International Symposium on Large Spatial Databases, Maine, USA, 1995 |
| [19] | Zhang X, Mamoulis N, Cheung D, et al. Fast Mining of Spatial Collocations [C]. The ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, USA, 2004 |
| [20] | Bembenik R, Rybinski H. FARICS: A Method of Mining Spatial Association Rules and Collocations Using Clustering and Delaunay Diagrams [J]. Journal of Intelligent Information Systems. 2009, 33(1): 41-64 |
| [21] | Shekhar S, Huang Yan. Discovering Spatial Co-location Patterns: A Summary of Results [J]. LNCS, 2001, 2 121: 236-256 |
| [22] | Sierra R, Stephens R. Exploratory Analysis of the Interrelation Between Co-located Boolean Spatial Features Using Network Graphs [J]. International Journal of Geographical Information Science, 2012, 26(3):441-468 |
| [23] | Shiode S. Analysis of a Distribution of Point Events Using the Network-Based Quadrat Method [J]. Geographical Analysis, 2008, 40(4): 380-400 |
| [24] | ZhouWenliang. The Agglomeration, Dispersion of Manufacturing and Its Policy Selection: the Research Based on Guangdong Province [M]. Beijing: Economic Science Press, 2010. (周文良. 制造业的集聚、扩散及其政策选择: 基于广东省的分析 [M]. 北京: 经济科学出版社,2010) |
| [25] | General Administration of Quality Supervision, Inspection. and Quarantine of The People's Republic of China. GB/T 4754-2002 Industrial Classification for National Economic Activities [S]. Beijing: China Zhijian Publishing House, 2007 (中华人民共和国国家质量监督检验检疫总局.GB/T 4754-2002 国家经济行业分类[S]. 北京: 中国标准出版社, 2007) |
| [26] | WuXuehua. Research on Regional Cluster of Manufacturing in China [M]. Beijing: Economic Science Press, 2010 (吴学花. 中国制造业区域集聚研究 [M]. 北京: 经济科学出版社, 2010) |
| [27] | Monseny J, López R, Marsal E. The Mechanisms of Agglomeration: Evidence from the Effect of Inter-Industry Relations on the Location of New Firms [J]. Journal of Urban Economics, 2011, 70(2/3): 61-74 |
| [28] | Wang Guohong. Research on Knowledge Spillover and Enterprise Learning in Industry Cluster [M]. Beijing: Science Press, 2010(王国红. 知识溢出与产业集群中的企业学习研究 [M]. 北京: 科学出版社, 2010) |
| [29] | Amiti M. Location of Vertically Linked Industries: Agglomeration Versus Comparative Advantage [J]. European Economic Review, 2005, 49(4): 809-832 |
 2015, Vol. 40
2015, Vol. 40


