文章信息
- 刘海龙, 钱海忠, 王骁, 何海威
- LIU Hailong, QIAN Haizhong, WANG Xiao, HE Haiwei
- 采用层次分析法的道路网整体匹配方法
- Road Networks Global Matching Method Using Analytical Hierarchy Process
- 武汉大学学报·信息科学版, 2015, 40(5): 644-651
- Geomatics and Information Science of Wuhan University, 2015, 40(5): 644-651
- http://dx.doi.org/10.13203/j.whugis20130350
-
文章历史
- 收稿日期:2013-07-23
2. 95851部队, 江苏 南京, 210046
2. Unit 95851, Nanjing 210046, China
空间数据现势性是地理信息系统的“生命”,直接影响着其使用价值与可持续发展。随着我国系列比例尺地理空间基础数据库的建成,下一步的建设重心已经从数据生产转为数据更新,数据更新已经成为测绘保障部门的常态化保障主题。道路网作为地理数据中变化最快的空间要素之一,其更新越来越受到人们的广泛关注。道路网更新的目的是对发生变化的部分进行修改,而道路网匹配技术是其中的关键技术之一。同时,由于道路网间存在多重类型的对应关系,其匹配也是道路网数据更新的难点之一,匹配效果的好坏直接影响到后续更新的正确性。
针对相邻比例尺道路网的匹配问题,文献[1]等提出了基于层次分析的道路匹配方法,文献[2]研究了全局寻优的矢量道路网自动匹配方法,文献[3]在研究多特征组合实体匹配中引入点、线实体环境相似度,并提出顾及环境相似的多特征组合匹配方法。需要说明的是,文献[1]中的方法主要针对道路本身进行处理,即进行分解和抽象。与此不同的是,本文所述的层次分析法是一种决策分析方法,侧重于对道路网各特征之间的关系进行综合分析。在多尺度道路网中,随着比例尺的变化,道路要素的几何形状和数据表达内容都有较大差异,这就造成了不同比例尺道路网的匹配相对于同一比例尺或者相近比例尺的道路网匹配有自己的特点。例如,不同尺度道路网拓扑关系很难保持一致性;匹配方式大多属于较为复杂的m∶n匹配关系。针对多尺度道路网的匹配问题,文献[4]根据道路网折线的匹配特点,提出了基于格网索引的折线-结点距离匹配算法,文献[5]将道路网数据处理成以“结点-弧段”表达的网络数据,通过预匹配、结点匹配、弧段匹配三个步骤,实现最终的匹配运算。
无论是相邻比例尺道路网数据的匹配还是多尺度道路网数据的匹配,均面临一个共性问题:很少将道路网视作一个整体,而是以各个弧段的形式进行处理,这在某种程度上不符合人类从整体到局部的认知习惯,也增加了匹配过程中的不确定性因素。另外,在道路匹配中,可能存在两个或多个对象的位置、形状的相似度非常高,但它们并不相互对应。因此,仅仅依靠几何特征进行匹配往往是片面的,需要综合采用多个指标进行相似分析。然而,在涉及多指标综合匹配分析时,均面临各指标的权值设定问题,以及以哪个指标为主的问题。目前许多算法中涉及到权值设定问题时,一般通过人为赋值,随意性较大,在某种程度上影响了匹配算法的精准程度。
本文从人类认知的角度出发,采用Stroke技术将琐碎复杂的道路网连接成一个整体,并利用线面相对位置关系进行候选匹配集的筛选,有效避免了漏匹配和过匹配情况的发生。在提取道路网Stroke的基础上,建立了一种多指标混合匹配的道路网匹配模型,并且在匹配指标的权重分配过程中,采用层次分析法综合分析各匹配指标的重要性程度,从而自动、合理分配权值,避免了由于权值设定所造成的误差,减少了主观因素参与,提高了匹配的精度和可靠程度。
1 道路网关联关系分析 1.1 道路网匹配关系道路网之间的匹配关系可表示为1∶0、0∶1、1∶1、1∶n、m∶n等几种。如果定义待匹配数据双方分别为源数据和目标数据,则两者的对应关系可由图 1表示。
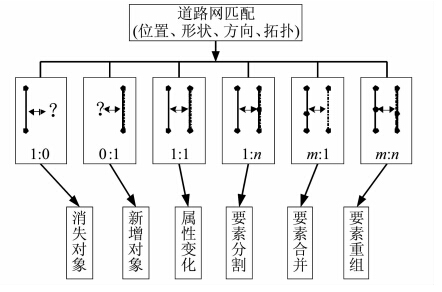 |
| 图 1 道路网匹配关系图Fig. 1 Road Network Matching Relationship |
道路网之间多重类型对应关系的存在,使得道路网的匹配问题变得十分困难,因此应尽量避免m∶n这种匹配情形的出现,也就是说把m∶n这种情形尽量转化为1∶n或者1∶1情形进行处理,从而减少匹配过程中的复杂度和不确定性,提高匹配准确率。道路网Stroke技术提供了一种把离散的道路弧段构建为完整道路的方法。
1.2 道路网Stroke模型有效的道路网结构认知是道路综合决策过程的第一步,一条完整道路的构建是将连续的路段按一定的规则综合而成。道路网Stroke模型便是根据视觉认知格式塔规则中的“连续性原则”提出的,即从人的视觉感受出发,表现为相同方向的元素容易被看成连在一起构成一条Stroke[6]。
道路网Stroke模型模拟了人工选取道路时人眼对道路长度的视觉判断,结合道路几何和语义属性对整个道路网进行分析。在道路网数据采集时,道路要素被分割成一条条弧段,弧段与弧段之间通过结点相连接。通常情况下,道路网的Stroke是在道路弧段的基础上生成的,通过判断两条道路弧段间的偏向角来组织道路网数据[7]。但是由于道路网等级繁多且关系较为复杂,单靠弧段间的偏向角来判断容易造成道路Stroke的误连接。如图 2所示,如果假定三条道路弧段 l1、l2、l3同属一个等级,称为“A道路”,这样,根据“良好连续性原则”,可以认为l3和l1是相连的,因为较之l1 l2在连接处的走向,l1 l3在连接处更接近一条直线,即两者之间的夹角更接近180°;如果l1、l2同属“B道路”类型,而l3属于“A道路”,根据相似性重组的原则,l2则和l1连接为同一条 Stroke。因此,在道路弧段重组中,需要综合考虑道路属性信息、形态趋势和弧段偏向角来具体判断[8]。
 |
| 图 2 道路Stroke生成示意图Fig. 2 Diagram of Generating Stroke |
将琐碎的道路弧段采用Stroke技术进行重新组织,形成一条完整的道路,为后续整体匹配分析打下基础。这种认知分析,更符合人类认知客观世界从总体到局部、从概略到细微、从重要到次要的顺序,具有明显的空间层次特征。
2 道路网相似度衡量指标的选取对于同名实体的相似度衡量,大多采用多个相似指标综合判断。对于线状实体(道路、河流等),通常从长度、形状、方向等特征入手,通过计算各指标相似性并加权求和来获取对象整体相似度。在计算过程中,不同方法利用的指标一般都大致相同,但各指标相似性的计算方法及其权值又略有差异。本文根据问题的特点给出了各项指标的计算方法,并通过层次分析方法自动确定各指标权值,进一步确定整体相似度,从而实现指标权值赋值的自动化。
2.1 位置相似度指标及其度量空间位置信息是地理实体空间表达的基础,位置上的接近程度可以由空间距离反映。Hausdorff距离可以反映两条线之间的整体距离,可有效衡量线实体间的远近程度[9],因此,本文采用Hausdorff距离来度量线要素的位置相似情况:
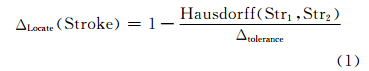
其中,Δtolerance为距离阈值。
2.2 形状相似度指标及其度量
长度可以很直观地反映线状要素的形状特征。如果同名道路实体长度相近,则它们存在匹配关系的可能性就越大,设LStroke1、LStroke2分别为两条Stroke的长度,则其相似性关系可表示为:
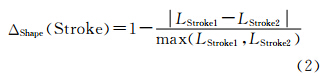
2.3 方向相似度指标及其度量
方向特征是描述线要素的又一个重要指标。本文采用顾及弧段长度的道路方向均值度量方法,即连接Stroke的特征点形成新的弧段,将各弧段的相关长度系数作为权值,对各弧段的方位角加权求值,以此作为度量线要素方向的指标。
如图 3所示,设Stroke特征点连线的长度为L,第i条线段(即相邻两个特征点之间的连线)的长度为Di,则相关长度系数为:

将该值作为计算方向均值的权值,得到描述整条道路Stroke方向的计算模型:
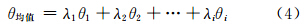
其中,θi为为第i条连线与x轴正方向的夹角。通过度量两条 Stroke之间的方向均值,得出方向相似性的计算公式:
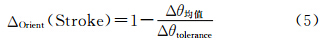
其中,Δθ均值为两条Stroke方向均值的差值,即Δθ均值=|θ均值1-θ均值2|;Δθtolerance为两条待匹配Stroke间的方向均值差异阈值。
 |
| 图 3 方向均值量化表达Fig. 3 Quantified Expressions of Direction |
拓扑结构相似性一般作为辅助要素判断线要素的匹配情况,一般通过比较弧段上结点关联的弧段数量以及弧段的方向来实现[10]。本文采取道路弧段上结点关联弧段的数量来衡量两条Stroke之间的拓扑相似性,计算公式为:

其中,NNum1、NNum2分别为两条Stroke上各结点所关联弧段的数量。
上述相似度衡量指标虽然可以作为道路匹配的重要依据,但由于指标太多,一方面涉及到各个指标之间的重要性排序问题,另一方面还涉及到各指标值的赋值问题。已有研究往往对各类指标手动赋予经验值,并进行归一化处理,这无疑增加了算法的不确定性。本文采用层次分析法对各个指标进行重要性分析,并自动计算所需权值,减少了算法的不确定性,提高了算法自动化程度。
3 基于层次分析法的相似权值自动确定方法确定因子权重是建立评价模型的重要步骤,权重的正确与否极大地影响着评价模型的正确性,因此,权值的确定是评价匹配精度的关键所在。在当前的很多匹配算法中,权值的确定一般通过专家经验设定,随意性较大,在某种程度上影响了匹配算法的精准程度。因此,为了减少人为设定权值所造成的误差,迫切需要建立更加科学的相似性评价模型,使得匹配算法更具精确性和可靠性,层次分析法提供了一种合理确定权值的方法。
3.1 层次分析法层次分析法是系统分析的数学工具之一[11],它把人的思维过程进行了层次化、数量化处理,并用数学方法为分析、决策、预报或控制提供定量的依据,是一种定性和定量分析相结合的方法。层次分析法的基本计算过程有构造判断矩阵、计算层次单排序、计算各层元素的组合权重、一致性检验。其中,判断矩阵的构造是进行层次分析的基础所在。根据各属性的重要程度,可构造如表 1所示的判断矩阵。
由于各实体间的变化情形复杂,大多由多种 变化类型共同作用而成,单纯采用位置特征判断 是否为同名空间实体,很可能得到与实际情况不相符的结果。因此,本文引入形状、方向等其他特征指标对上述位置特征判断进行有效约束,最终的整体相似度是综合考虑多个特征指标值所得到的。另外,在空间实体变化过程中,各特征指标的贡献率是有差异的,分析和判断实体间的相似情况时,就不可避免地涉及到权值设定问题。
为了避免人为设定权值过程的随意性,即“强化”或者“弱化”某些特征指标,有必要对各特征指标进行重要性分析。在众多相似性指标中,空间位置指标是描述空间实体变化的重要判断依据,而且,实体的位置信息在一定程度上会影响到其他空间特征[12]。同名空间实体虽存在差异性,但从理论上来讲,同名实体在空间位置上应该是完全重合的(虽然这是不可能做到的),基于这种思想,可以认为同名实体在空间位置上是非常接近的[13]。无论是点实体、线实体还是面实体,只要确定了其位置信息和形状特征,该实体的空间特征则可以大致确定[14]。因此,空间位置特征重要性最高;形状特征作为反映空间实体的直观形态,其重要性次之;方向特征作为辅助判断指标,其重要性相对较弱;而拓扑特征通常作为约束判断条件,其重要性最弱。
由于语义特征的相似性度量通常受到不同领域各自术语、命名习惯和分类体系等的影响,判断较为复杂,而且由于在构建道路网Stroke时,将同一等级的道路连接为一条Stroke,而这些道路有可能名称不同,因此很难用语义特征来判断相似性情况,故本文中暂不考虑语义特征。
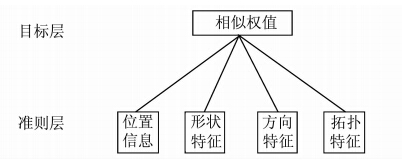
3.3 相似指标层次分析模型构建根据以上分析,建立图 4所示的层次分析模型。
 |
| 图 4 相似指标权值的层次分析模型Fig. 4 Analytic Hierarchy Model of Similar Index |
在图 4中,目标层为 A,准则层中的位置信息、形状特征、方向特征、拓扑特征分别用B1、B2、B3、B4表示。就层次分析法的通用设置而言,表 1所示的判断矩阵中,bij为对于A而言,Bi与Bj相对重要性的数值表现形式,取值通常为1,2,3,…,9及它们的倒数,例如,1表示Bi与Bj一样重要,3表示Bi比Bj重要一点,5表示Bi比Bj重要,…,它们之间的数2,4,6等表示介于其间的重要性判断。其中,bij满足互反性,即若Bi与Bj相比得bij,则表示Bi比Bj稍微重要;同时,Bj与Bi相比所得bij=1/bij=1/3。
根据各指标重要性分析结果,相对于其他指标,空间位置特征重要等级最高,本文通过选取专家经验数据进行实验分析,得到以下权值信息的相对重要性赋值(见表 2)。
| A | B1 | B2 | B3 | B4 |
| B1 | 1 | 2 | 3 | 5 |
| B2 | 1/2 | 1 | 2 | 3 |
| B3 | 1/3 | 1/2 | 1 | 2 |
| B4 | 1/5 | 1/3 | 1/2 | 1 |
对于判断矩阵B,计算满足 Bx =λmax x 的特征值和特征向量,λmax为最大特征值,x 的分量即为相应的单排序权值。
权重系数的大小反映了每一相似特征指标对系统相似度影响的重要性程度。矩阵B中的元素bij根据以上判断矩阵,各权值大小的计算步骤如下。
1) 采用和积法对判断矩阵的每一列元素进行归一化处理:
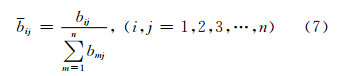
2) 将每一列进行归一化处理后的判断矩阵按行相加:

3) 对向量ω=[ω1 ω2 … ωn]T归一化处理:
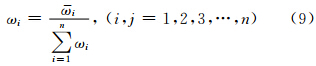
由此可得,ω =[ω1 ω2 … ωn]即为权值。其中,判断矩阵的最大特征值为:

判断矩阵B的特征向量及最大特征值可通过式(8)、式(10)分别求得。其特征向量为 ω ,最 大特征值 ω =[0.848 7 0.466 7 0.269 4 0.151 3]。
从理论上讲,任何判断矩阵B都应具有一致性,即矩阵B的最大特征值λmax=n,但由于比较在两两之间进行,难免会因为人们对事物认识的模糊性和多样性而造成判断矩阵的不一致,这就可能导致λmax>n情形出现。为检验判断矩阵B的有效性,需对其进行一致性检验,一致性指标C为:
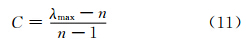
另外,判断矩阵B的一致性还具有随机性,这种随机一致性可用平均随机一致性指标R表示,表 3所示为1~10阶矩阵的平均随机一致性指标值,则相对一致性比例为:

一般认为,当CR<0时,判断矩阵具有满意的一致性,否则需对判断矩阵进行调整和修正。
| 阶数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| R | 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
计算一致性指标 C=(λmax-n)/(n-1)= (4.014 5-4)/(4-1)=0.004 8。为了检验相对一致性情况,本文实验中,R取0.90,由式(12)可计算得到相对一致性比例CR=C/I=0.004 8/0.90=0.005 3<0.1,判断矩阵满足一致性要求。利用式(9)对特征向量ω进行归一化处理,可以得到各相似评价指标的权重大小分别为: wLocate=0.483,wShape=0.272, wOrient=0.157, wTop=0.088。根据以上分析,整体相似度可表示为:
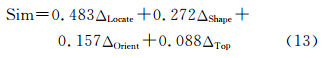
在空间数据匹配过程中,随着数据库中数据量的不断增大,匹配时间也随之增加,其中大部分时间都用在了候选匹配集的筛选上,这样难免影响到了匹配效率。如何快速获取候选匹配集,是提高空间数据匹配效率的有效途径[15]。为了有效减少匹配过程中的索引时间,首先对待匹配数据进行预处理。本文采用线面相对位置关系来筛选目标数据中的道路目标,详细流程如图 5所示。
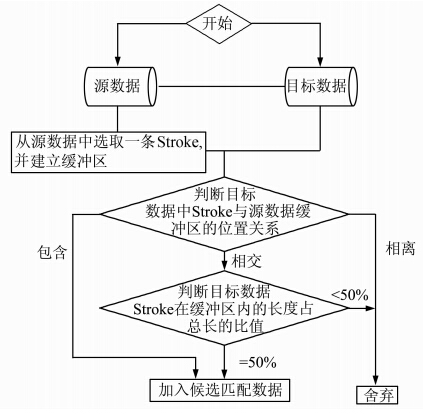 |
| 图 5 基于线面位置关系的匹配集筛选流程Fig. 5 Selecting Process of Matching Candidates |
1) 从源数据中选取一条道路Stroke(Stroriginal),为其建立一个缓冲区StrBuffer。
2) 判断目标数据中组成道路Stroke的道路弧段(Strreference)与该StrBuffer的的位置关系:如果Strreference中存在道路弧段与StrBuffer相离,则源数据中的道路Stroke(Strcundidale)不属于Stroriginal的候选匹配集,予以舍弃;如果Strreference完全包含在StrBuffer中,则将其纳入候选匹配集;如果Strreference中存在道路弧段与StrBuffer相交,并且Strreference中大于50%的长度在StrBuffer内,则将其纳入候选匹配集,否则予以舍弃。
3) 将源数据与筛选出的匹配集加入相似分析模型中以作进一步判断。
阈值设定是筛选匹配集的关键所在,本文采用动态阈值设定的方法判断源数据中的道路是否在目标数据道路缓冲区内,具体方法为:初始设定一个较小阈值进行筛选分析,统计筛选成功率;然后分别逐步增大和缩小阈值范围,并统计筛选的成功率;最后选择筛选成功率最高的阈值大小作为最后设定的阈值,本文中该阈值设定为50%。
4.2 实验结果分析
实验采用某地不同比例尺道路网数据,分别为源数据(图 6(a))和目标数据(图 6(b))。
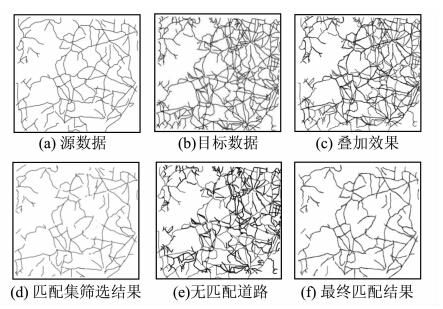 |
| 图 6 匹配结果Fig. 6 Matching Results of Two Road Networks |
图 7所示为从图 6(a)、6(b)中选取的部分道网数据匹配效果,对应的相似度评价统计如表 4所示。由图 7(a)可以看出,Str3 由弧段 R8R2、R2R6及R6R9组成,而图 7(b)中,Str4是由弧段 T14T2、T2T15、T15T10、T10T16及T16T17组成。从 视觉上看,虽然Str3和Str4在局部之间存在相似性较高的形态,但在整体形态上差距明显,采用Hausdorff距离判断,两者在位置上差异较大,同时在局部方向特征上也存在明显差异(弧段R8R2弧段处尤为明显),导致综合判断后,整体相似度较低,出现了误匹配。下一步将采用整体匹配和局部匹配相结合的策略,来进一步提高匹配方法的正确率。
 |
| 图 7 部分道路匹配效果Fig. 7 Matching Results of Partial Road Networks |
| 匹配数据 | 相似指标分析 | 是否匹配 | |||||
| 位置信息 wLocate=0.483 |
形状特征 wShape=0.272 |
方向特征 wOrient=0.157 |
拓扑特征 wTop=0.088 | 整体相似度 | |||
| 例一 | Str1 Str2 | 0.825 | 0.932 | 0.833 | 0.6 | 0.836 | 是 |
| 例二 | Str3 Str4 | 0.431 | 0.817 | 0.526 | 0.571 | 0.563 | 否 |
| 例三 | Str5 Str6 | 0.843 | 0.957 | 0.875 | 0.75 | 0.868 | 是 |
在匹配集的筛选过程中,对单条道路Stroke选择合适的缓冲区半径较为关键。目前大多算法中涉及到阈值设定的部分都采用经验值,本文实验采用在一定范围内动态设置阈值的方法,即初始设定一个最小值,逐步增加阈值,统计最优匹配结果,经过多次实验测试,缓冲区半径设为50 m时,筛选的时间和效率达到了最优化,图 6(d)所示为候选匹配集筛选结果。
根据式(13),进一步对源数据和候选匹配集进行匹配分析,可得出最终匹配结果,如图 6(f)所示,图 6(e)中粗线所示为无匹配道路数据,详细统计结果如表 5所示。
| 数据集 | Stroke数量 | 新增 | 消亡 | 筛选率 | 匹配成功率 |
| 源数据 | 140 | 96 | 12 | 88.54% | 96.36% |
| 目标数据 | 455 |
经过验证可以发现,本文中的匹配结果与目视判别的结果基本一致,符合人类的认知习惯,说明本文的匹配方法是正确的,实验结果表明:
1) 基于人类认知客观世界从整体到局部这一思想,将琐碎的道路弧段通过Stroke技术转化成完整的道路,从而进行整体匹配分析,可有效避免m∶n匹配类型的出现,降低算法的不确定性。
2) 基于线面位置空间关系的候选匹配集筛选方法,有利于剔除冗余数据,缩小了待匹配数据的范围,提高了后续匹配的效率。
3) 综合采用线实体的位置、形状 、方向等特征计算道路的相似度,并采用层次分析法合理地确定各相似指标的权值,匹配结果较为科学。
4) 各相似指标权值的自动分配,可有效避免因人为设置权值所造成的不确定性因素。
5 结 语道路网匹配涉及不同来源、不同尺度的道路数据,且由于数据采集过程中的误差,匹配情形较为复杂,因此,各指标的相似性计算方法和准确性都会影响匹配的置信水平。本文从人类对客观世界的认知习惯入手,将离散的道路弧段通过Stroke技术形式化表达,综合运用多个相似指标匹配分析,并采用层次分析法对各指标的权值进行合理分配,有效避免了因权值设置的随意性而造成的误匹配。
本文只对相邻比例尺的道路网数据匹配进行了研究,多尺度空间数据间的匹配关系远比相邻比例尺空间数据的匹配问题更复杂,因此,需要进一步探寻更多尺度之间的匹配原理与方法。此外,对匹配结果进行质量评估是保证空间数据正确性和一致性的关键举措,也是空间数据更新的基本要求,这也是下一步需要重点关注的研究方向。
| [1] | Chen Jun, Hu Yungang, Zhao Renliang, et al. Road Data Updating Based on Map Generalization[J]. Geomatics and Information Science of Wuhan University, 2007, 32(11): 1 023-1 027(陈军, 胡云岗, 赵仁亮, 等. 道路数据缩编更新的自动综合方法研究[J]. 武汉大学学报·信息科学版, 2007, 32(11):1 023-1 027) |
| [2] | Zhao Dongbao, Sheng Yehua.Research on Automatic Matching of Vector Road Networks Based on Global Optimization[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4):416-421(赵东保, 盛业华. 全局寻优的矢量道路网自动匹配方法研究[J]. 测绘学报, 2010, 39(4):416-421) |
| [3] | Wu Jianhua.Entity Matching Methods Based on Combining Multi-Similarity-Characteristics Considering Environment Similarity[J]. Geography and Geo-Information Science, 2010, 26(4): 1-6(吴建华. 顾及环境相似的多特征组合实体匹配方法[J]. 地理与地理信息科学, 2010, 26(4):1-6) |
| [4] | Chen Yumin, Gong Jianya, Shi Wenzhong.A Distance-based Matching Algorithm for Multi-scale Road Networks[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1):84-90(陈玉敏, 龚健雅, 史文中. 多尺度道路网的距离匹配算法研究[J]. 测绘学报, 2007, 36(1):84-90) |
| [5] | Huang Wei, Jiang Jie. Simple Geometry Matching of Multi-scales Spatial Data[J]. Remote Sensing Information, 2011(1):27-31(黄蔚, 蒋捷. 多尺度矢量简单几何实体数据几何匹配方法研究[J]. 遥感信息, 2011(1):27-31) |
| [6] | Thomson R C, Richardson D E. The 'Good Continuation' Principle of Perceptual Organization Applied to the Generalization of Road Network[C]. The 19th International Cartographic Conference, Ottawa, Canada, 1999 |
| [7] | Zhang M. Methods andImplementations of Road-network Matching[D]. Munich, Germany: Technical University of Munich, 2009 |
| [8] | Qian Haizhong, Zhang Zhao, Zhai Yinfeng, et al. Road Selection Method Based on Character Recognition, Stroke and Polarization Transformation[J]. Journal of Geomatics Science and Technology, 2010, 27(5): 371-378(钱海忠, 张钊, 翟银凤, 等. 特征识别、Stroke与极化变换结合的道路网选取[J]. 测绘科学技术学报, 2010, 27(5):371-378) |
| [9] | Mustière S, Devogele T. Matching Networks with Different Levels of Detail[J]. Geoinformatica, 2008, 12(4):435-453 |
| [10] | Deng Min, Xu Kai, Zhao Binbin, et al.A Hierarchical Approach for Nodes Matching Based on Structural Spatial Relations[J]. Geomatics and Information Science of Wuhan University, 2010, 35(8): 1 023-1 027(邓敏, 徐凯, 赵彬彬, 等. 基于结构化空间关系信息的结点层次匹配方法[J]. 武汉大学学报·信息科学版, 2010, 35(8):1 023-1 027) |
| [11] | Saaty T L. The Analytic Hierarchy Process[M]. New York: Mc Gtaw Hill, 1980 |
| [12] | Ding Hong. A Study on Spatial Similarity Theory and Calculation Model[D]. Wuhan: Wuhan University, 2004(丁虹. 空间相似性理论与计算模型的研究[D]. 武汉: 武汉大学, 2004) |
| [13] | Liu Dongqin, Su Shanwu.Study on Spatial-Position Matching Technology of Multi-scale Databases[J]. Science of Surveying and Mapping, 2005, 30(2):78-80(刘东琴, 苏山舞. 多空间数据库位置匹配方法及其应用[J]. 测绘科学, 2005, 30(2):78-80) |
| [14] | Egenhofer M, Franzosa R. Point-Set Topological Spatial Relationships[J]. International Journal of Geographical Information Systems, 1991, 5(2): 161-174 |
| [15] | Shao Shiwei. Researches and Applications on Polygon Entity Matching for Multi-scale Vector Data Based on Geometric Features[D]. Wuhan: Wuhan University, 2011(邵世维. 基于几何特征的多尺度矢量面状实体匹配方法研究与应用[D]. 武汉: 武汉大学, 2011) |
 2015, Vol. 40
2015, Vol. 40




