文章信息
- 王珂, 张周威
- WANG Ke, ZHANG Zhouwei
- 矢栅一体化拓扑关系的度量描述研究
- Quantitative Representation of Topology Relations Based on Integrative Data Model of Vector and Raster
- 武汉大学学报·信息科学版, 2015, 40(5): 638-643
- Geomatics and Information Science of Wuhan University, 2015, 40(5): 638-643
- http://dx.doi.org/10.13203/j.whugis20130357
-
文章历史
- 收稿日期:2013-07-28
2. 中国科学院遥感与数字地球研究所, 北京, 100101
2. Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China
文献[1]从心理认知的角度研究空间关系,文献[2]提出了空间关系理论的基本框架。代表性的空间关系模型有4交模型[3]、9交模型[4]、区域连通演化模型[5]、基于Voronoi图的9交模型[6]、4交差模型[7]和基于模糊学的拓扑关系模型[8, 9]。但是,形式化空间关系描述方法忽略了目标的度量特性。这些空间关系很难推断目标的真实空间特性,因此,定性描述的空间关系易受误差和不确定性影响[10]。同时,这种粗略的空间关系分类很难满足GIS空间信息定量分析的要求,尤其是动态信息分析[11]。由此学者们进行了拓扑关系的度量化研究[12, 13, 14, 15],并将其应用于GIS和遥感领域[8, 16]。
但是,学者们多以矢量模型进行研究。以9交模型为例,文献[12, 13, 14]分别对面/面、线/面、线/线间拓扑关系的度量化进行了研究。但是在R2空间,点、线和面等对象的边界和内部概念是不同的(例如线目标由0-D不连续的点作为边界和1-D连续的线为内部;而面目标则是由1-D连续的线作为边界和2-D连续的面作为内部),所以未能实现形式化的统一表达。所以,以矢量空间数据模型为基础的度量化描述存在不足。
文献[17]提出采用两级Morton码的方式来构建矢量栅格一体化模型。文献[18]在UML语言的基础上提出了参数化地理对象模型,用以集成表达矢量和栅格模型。文献[19]利用一系列的映射将矢量和栅格整合起来。文献[20]用一种原子形式的基本数据结构来整合矢量和栅格数据模型。本文借助矢量栅格一体化模型研究拓扑关系的度量化表达,利用该模型中的矢量表达,以9交模型来确定定性拓扑关系;利用栅格表达,建立拓扑关系的交叠分量和邻近分量来描述拓扑关系的度量信息。由于模型点、线和面目标均可用栅格来表现,所以可以形式化地描述不同类型地理目标间拓扑关系(点/点、点/线、点/面、线/线、线/面和面/面)的度量信息。
1 矢栅一体化数据模型本文以文献[17]提出的矢量栅格一体化模型为基础,研究空间关系的度量描述。为了充分发挥矢量栅格一体化模型的优势,对该模型引入矢量模型的精确定位信息:
1) 对于点对象,记录栅格位置,同时记录点对象 在R2空间的准确定位信息;
2) 对于线对象,记录各弧段起始点、终结点及中间节点的R2空间定位信息;
3) 对于面对象,记录面域边界弧段上中间节点的R2空间定位数据信息。
如此,空间数据模型综合了 R2和Z2 两个空间的特点来描述地理目标(见图 1)。即所有地理目标在矢栅一体化数据模型中,均结合矢量和栅格数据模型特点来描述。
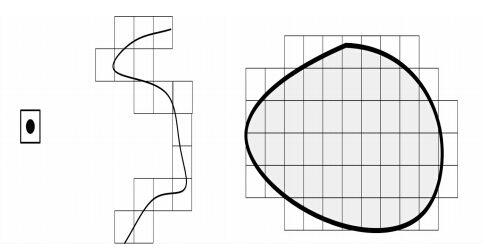 |
| 图 1 矢栅一体化数据模型中的点线面对象表达Fig. 1 Description of Point,Line and Area in Integrative Data Model of Vector and Raster |
定性的拓扑关系借助9交模型来实现。矢量栅格一体化数据模型中定性拓扑关系会有如下情况:矢量表达下的两目标相离或相切,但栅格表达下出现重叠现象;栅格表达下两目标相合,但是矢量表达下却为相交,如图 2所示。针对这种现象,本文给出如下设定:
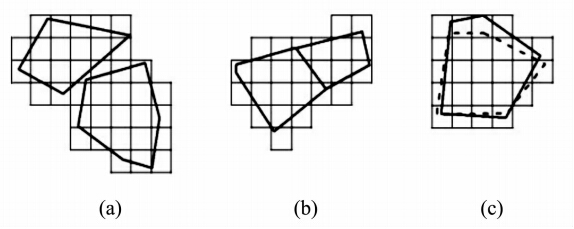 |
| 图 2 矢栅一体化数据模型中的拓扑关系差异Fig. 2 Difference of Topology Relations in Integrative Data Model of Vector and Raster |
1) 若两矢量目标相离,但栅格区域重叠,拓扑关系仍为相离(图 2(a));
2) 若两矢量目标相切,但是栅格区域重叠,拓扑关系仍相切(图 2(b));
3) 若两矢量目标相交,但栅格区域相合,拓扑关系仍为相交(图 2(c))。
所以定性拓扑关系仅由矢量模型来确定,栅格模型只用于度量化参数的确定。拓扑关系被分为两类:第一类为相交、相切、包含和相合,栅格模型中必然有重叠栅格存在,引入交叠分量来补充描述度量信息;第二类为相离,主要用邻近分量来进行度量信息的补充描述。
3 交叠分量当两个目标相交,相交部分的大小以及如何相交等特征,无法从定性的拓扑关系中得到。因此,其度量信息是必要的。本文借助矢栅一体化模型,引入交叠分量二元组(CA,CB)来补充描述拓扑关系。
由于矢量栅格一体化数据模型中,点、线、面等对象均被描述为一个或者多个栅格。所以,交叠分量可以用于描述所有类型的拓扑关系,即点/点、点/线、点/面、线/线、线/面、面/面间的拓扑关系。
给定源目标 B和参考目标A(见图 3),两对象重叠栅格数目为6。交叠分量用二元组(CA,CB)表示,CA和CB分别为相交的栅格数目与目标A和B的栅格数目之比。CA和CB的取值范围为[0, 1],当拓扑关系为相离和相切时,其取值不一定为0 (图 3(a)、3(b));当相合时,取值为1;相交时,取值范围为(0,1); 当A包含B时,CA取值范围为(0,1],CB取值为1,反之亦然。CA和CB的计算公式为:
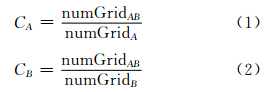
其中,numGridAB表示目标A和B间重叠栅格数目;numGridA和numGridB分别表示A和B所占栅格总数。
 |
| 图 3 目标A与B间的重叠栅格Fig. 3 Grids of Intersection Between Object A and B |
另外一种特殊情况是:由于两目标的缠绕等作用,使得其相交部分内部不连通,即形成多个独立的相交部分。 如图 4所示,图 4(a)线/线相交形成多个交点,图 4(b)线/面相交形成两条不相接的弧段,而图 4(c)面/面相交则形成两个独立的面。对于线/线而言,由于两目标缠绕而造成多个交点,线/面的相交部分则为两段独立的弧段,而面/面的相交部分则为两个独立的面对象。为更好区分相交部分是否为连通区,本文利用多个二元组来表达两目标间的交叠分量。
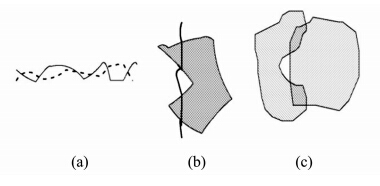 |
| 图 4 缠绕目标间的拓扑关系Fig. 4 Topology Relations Between Two Twining |
首先定义相交区为一个独立的点或者内部连通的弧段或区域。两目标间相交或相切时,重叠的栅格部分可能形成多个相交区。交叠分量表示 为{(CA1,CB1),(CA2,CB2),…,(CAn,CBn)},其中n表示相交区的个数。则式(1)和(2)分别变为:
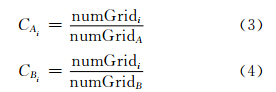
其中, numGridi为第i 个相交部分的栅格数。交叠分量主要用于两目标相交、相切、相合和包含的拓扑关系。当两目标间的拓扑关系为相离时,交叠分量取值为0,无法给出恰当的度量信息。因此,本文引入邻近分量来更好地补充描述相离关系中两目标间的“相离程度”。
4 邻近分量邻近分量由二元组来描述,其中的两个变量分别表示最大距离和最小距离。栅格数据满足统计学中的样本最主要的两个特点,即独立性和代表性。图 1中,点是以独立栅格来表达,而线和面则是以一组栅格来表达。每个栅格均可由一组量化的坐标(行列号或栅格中心位置)来唯一对应,并且每个栅格间均无交叠现象,彼此独立,所以每个栅格均具有独立性。同时,每个栅格都有其属性,该属性值代表了整个栅格所占的空间区域的属性,其所有栅格还表现了总体的结构和边缘等性质,所以具有代表性。因此,将栅格数据作为统计学中的样本来进行分析,并应用于拓扑关系邻近分量的确定。采用欧氏距离来度量各个栅格间的距离,设i和j代表两个栅格(样本),目标A中栅格i和目标B中栅格j间的距离为disij。目标A和B栅格数目为m和n,形成m×n的样本间距离矩阵 D ;
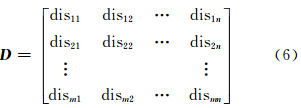
然后利用多元统计的系统聚类方法中的最短距离法和最长距离法来求得两个样本集,即栅格表达的目标A和B之间的距离,如式(7)、(8)所示:
最短距离:
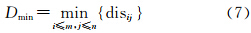
最大距离:
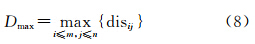
则邻近分量可以表示为(Dmin,Dmax)。
5 实例分析根据所提出的交叠分量和邻近分量,本文利用有序三元组来描述两目标间的拓扑关系定性和度量信息,如式(9)所示:
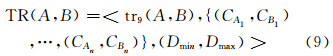
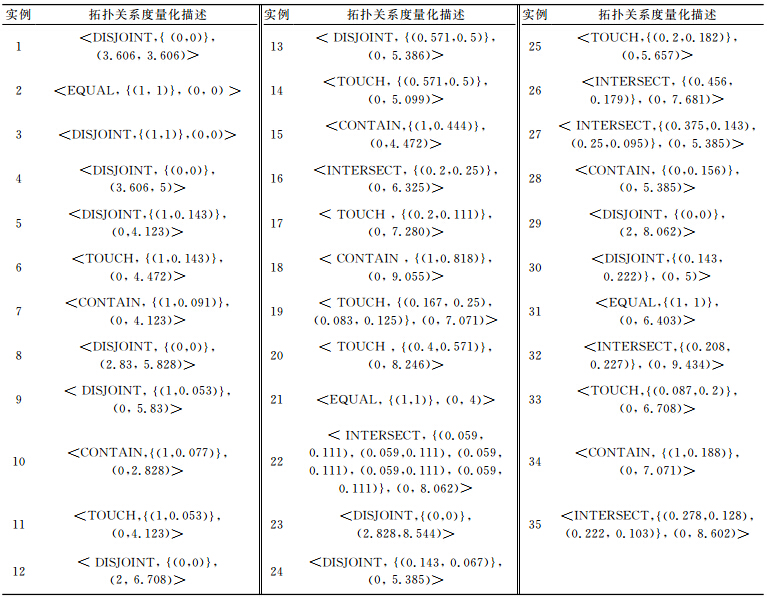
其中,TR(A,B)表示度量化的目标A和B之间的拓扑关系;tr9(A,B)为9交模型下的定性拓扑系;二元组(CA,CB)和(Dmin,Dmax)分别表示目标A和B的交叠分量和邻近分量。图 5给出了35种具有代表性的点、线、面目标间的拓扑关系作为实例进行描述和分析。表 1给出了图 5中目标A和B之间度量化的拓扑关系。
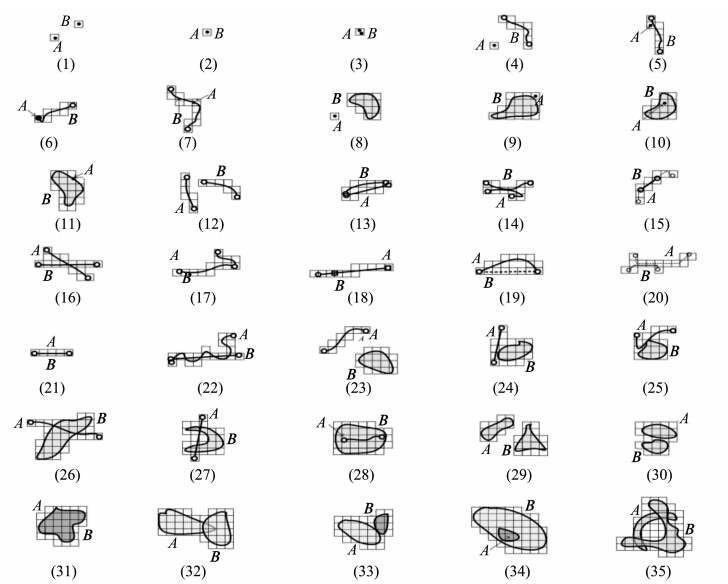 |
| 图 5 具有代表性的矢量栅格一体化拓扑关系描述Fig. 5 Representative Topology Relations Based on the Integrative Data Model of Vector and Raster |
在图 5(1)、5(4)、5(8)、5(12)、5(23)和5(29)中,9交模型下的拓扑关系为相离,交叠分量均为(0,0),而邻近分量通过最大、最小距离来描述两目标间的相离情况。当两目标均为点时,最大、最小值相同(图 5(1));在图 5(3)、5(5)、5(9)、5(13)、5(24)和5(30)中,虽然两目标拓扑关系也为相离,但是栅格表达有重叠现象,此时交叠分量不为(0,0);当两目标间拓扑关系为包含关系时(图 5(7)、5(10)、5(15)、5(18)、5(28)和5(34)),交叠分量二元组中,必 有CA=1或CB=1,且邻近分量可表达为(0,Dmax),且Dmax≠0;当拓扑关系为相合时,邻近分量与包含关系相同,但是交叠分 量均为(1,1);图 5(16)、5(26)和5(32)中,拓扑关系为相交,交叠两分量均不为0,且邻近分量Dmin=0,而Dmax≠0;而对于相切的拓扑关系而言(图 5(6)、5(11)、5(14)、5(17)、5(19)、5(20)、5(25)、5(33)),虽然交点可能仅为一个点,但是栅格的重叠数可能大于1,此拓扑关系的度量化描述特点为:其交叠分量CA≠0且CB≠0,而Dmin=0,Dmax≠0。
以上的拓扑关系描述较简单,在相切和相交关系中,交集区连通,而很多情况下,由于两目标的缠绕,交集区域可能是多个独立的子区域组成的。本文用二元组来分别表示交叠分量,从交叠分量中二元组的个数可以了解两目标间的相交次数,从而可以充分地认知目标间的相交或者相切拓扑关系。由于矢量与栅格模型的不确定性对该模型的影响,所以本文只从理论上对该模型进行分析,对于栅格的尺度则是由应用目的而定。 6 结 语
基于9交模型拓扑关系,本文引入了交叠分量和邻近分量来描述该拓扑关系的度量信息,从而更为有效地描述目标间的拓扑关系。鉴于点、线、面三种对象维度的不同(零维、一维和二维),基于 R2 空间的矢量数据模型,无法有效地形式化描述拓扑关系的度量信息。因此,本文利用矢量栅格一体化数据模型实现拓扑关系的度量化研究。借由目标间栅格重叠比率获得交叠分量,借助栅格的统计学意义计算最短和最大距离,从而确定邻近分量。实例分析表明,本文提出的三元组描述模型对目标间拓扑关系提供了更为详尽和有效的描述。在接下来的工作中,将对矢量栅格一体化数据模型中栅格大小对度量信息描述的影响作进一步研究。
| [1] | Freeman J. The Modeling of Spatial Relations[J]. Computer Graphics and Image Processing, 1975, 4:156-171 |
| [2] | Boyle A R, Dangrmond J, Marble D F, et al. Final Report of a Conference on the Review and Synthesis of Problems and Directions for Large Scale Geographic Information System Development[R]. National Acronautics and Space Administration, USA, 1983 |
| [3] | Egenhofer M J, Herring J. Categoring Binary Topological Relationships Between Regions, Lines, and Points in Geographic Databases[R]. University of Maine, Maine, 1991 |
| [4] | Egenhofer M J, Franzosa R. Point-Set Topological Spatial Relationships[J]. International Journal of Geographical Information Systems, 1991, 5(2): 161-174 |
| [5] | Randell D, Cui Z, Cohn A. A Spatial Logical Based on Regions and Connection[C]. The 3rd International Conference on Knowledge Representation and Reasoning, New York, 1992 |
| [6] | Chen J, Li C, Li Z, et al. A Voronoi-Based 9-Intersection Model for Spatial Relations[J]. International Journal of Geographical Information Science, 2001, 15 (3): 201-220 |
| [7] | Deng Min, Liu Wenbao, Feng Xuezhi. Generic Model of Topological Relations Between Spatial Regions in GIS[J]. Acta Geodaeticaet Cartographica Sinica, 2005, 34(1): 85-90(邓敏, 刘文宝, 冯学智. GIS面目标间拓扑关系的形式化模[J].测绘学报. 2005, 34 (1):85-90) |
| [8] | Shi W, Liu K. A Fuzzy Topology for Computing the Interior, Boundary, and Exterior of Spatial Objects Quantitatively in GIS[J]. Computer & Geosciences, 2007, 33: 898-915 |
| [9] | Liu K, Shi W. Quantitative Fuzzy Topological Relations of Spatial Objects by Induced Fuzzy Topology[J]. International Journal of Applied Earth Observation and Geoinformation, 2009, 11:38-45 |
| [10] | Deng Min, Li Chengming, Liu Wenbao. Description of Spatial Relations Between Area Objects Combing Topology with Metrization[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 164-169. (邓敏,李成名,刘文宝. 利用拓扑和度量相结合的方法描述面目标间的空间关系[J]. 测绘学报,2002, 31(2):164-169) |
| [11] | Liu W. Models of Data Quality and Dynamic Spatial Relations in GIS-T [R]. Southeast University, Nanjing, 1998 |
| [12] | Egenhofer M J, Shariff R. Metric Details for Natural-Language Spatial Relations[J]. ACM Transactions on Information Systems, 1998, 16(4): 295-321 |
| [13] | Shariff R. Natural-Language Spatial Relations: Metric Refinements of Topological Properties[D]. Maine: University of Maine, 1996 |
| [14] | Nedas K, Egenhofer M. Metric Details of Topological Line-Line Relations[J]. International Journal of Geographic Information Science, 2007, 21(1): 21-48 |
| [15] | Egenhofer M J, Matthew P D. Topological Relations from Metric Refinements[C]. The 17th ACM SIGSPATIAL Int. Conference on Advances in GIS, Seattle, Washington, 2009 |
| [16] | Liu Y, Guo Q, Kelly M. A Framework of Region-based Spatial Relations for Non-overlapping Features and Its Application in Object Based Image Analysis[J]. ISPRS Journal of Photogrmmetry & Remote Sensing, 2008, 63:461-475 |
| [17] | Gong Jianya. An Unified Data Structure Based on Linear Quadtrees[J]. Acta Geodaeticaet Cartographica Sinica, 1992, 21 (4):259-266.龚健雅. GIS中矢量栅格一体化数据结构的研究[J]. 测绘学报, 1992, 21(4): 259-266 |
| [18] | Kjenstad K. On the Integration of Object-Based Models and Field-based Models in GIS [J]. International Journal of Geographical Information Science, 2006, 20(5):491-509 |
| [19] | Cova T J, Goodchild M F. Extending Geographical Representation to Include Fields of Spatial Objects[J]. International Journal of Geographical Information Science, 2002, 16: 509-532 |
| [20] | Goodchild M F, Yuan M, Cova T J. Towards a General Theory of Geographic Representation in GIS[J]. International Journal of Geographical Information Science, 2007, 21(3):239-260 |
 2015, Vol. 40
2015, Vol. 40