文章信息
- 段平, 盛业华, 张思阳, 吕海洋, 王亭
- DUAN Ping, SHENG Yehua, ZHANG Siyang, LV Haiyang, WANG Ting
- 顾及异向性的局部径向基函数三维空间插值
- A 3D Local RBF Spatial Interpolation Considering Anisotropy
- 武汉大学学报·信息科学版, 2015, 40(5): 632-637
- Geomatics and Information Science of Wuhan University, 2015, 40(5): 632-637
- http://dx.doi.org/10.13203/j.whugis20130422
-
文章历史
- 收稿日期:2013-08-21
空间插值是根据有限的采样点集建立插值函数,并将任意地理空间坐标代入插值函数中估算该点的某种属性值,重建整个空间场。为了简化空间场的表达,将三维地理现象投影到二维空间中进行插值。但是,真实地理空间是三维的,二维空间场的表达与插值无法准确刻画地理现象在三维空间的真实分布和变化特征,需要采用三维空间场描述和表达三维空间的地理现象,通过三维空间插值方法建立三维空间场的函数A=f(x,y,z)来描述和表达三维空间的地理现象。
径向基函数(radial basis function,RBF)具有形式简单、求解方便等优点,在地质勘探、地形表面、土壤重金属等方面有着广泛应用。RBF插值分为全局RBF插值和局部RBF插值。全局RBF插值使用全部的已知节点构建RBF并对插值点进行属性计算。当节点数据量大时,会呈现插值矩阵是奇异矩阵且无法解算或矩阵求逆困难等问题,最终导致全局RBF插值失败[1]。局部RBF插值可以解决全局RBF插值出现的问题,主要利用插值点邻近范围内的节点来构建基函数进行局部RBF插值[2]。在三维空间下,局部RBF插值中的邻近范围通常定义为三维球体,但存在两个问题: ① 球体半径设置过大导致选取的参考点数目过多,影响插值速度;反之,选取的参考点数目过少,影响插值精度。 ② 三维球体的设置被认为在三维空间中各个方向对插值点的影响相同,即各向同性。但在实际情况下,三维地理空间数据存在着各向异性,三维球体的搜索策略没有顾及空间数据的各向异性。
为了解决三维空间中局部RBF插值存在的上述问题,本文通过地统计学中变异函数计算各个方向的变程,根据变程设置椭球体的参数并将其作为邻近搜索工具,使得在三维局部RBF插值过程中参考点的选取更为合理,从而得到更准确的插值结果。
1 三维空间局部RBF插值方法 1.1 方向性探索三维空间插值中,采样点的分布与采样仪器方向、分布等特性相关。例如,河流的悬沙含量、污染物浓度等,这些数据垂直方向与水平方向的尺度相差较大,并且整体趋势与坐标轴形成一定的夹角。考虑各向异性时,如果直接对原始数据进行变异函数计算,将三个轴向的变程设置为搜索椭球体的三个轴长,可能导致待插值点邻近范围内的参考点很少甚至没有,最终导致插值失败,如图 1(a)所示。为了避免上述情况,本文对原始数据进行主成分分析得到三个正交的坐标系,将数据旋转到新的坐标系下,沿着各个轴向分别计算变程,将变程设置为椭球体的轴长,使得局部RBF插值中椭球体能搜索到参考点,如图 1(b)所示。
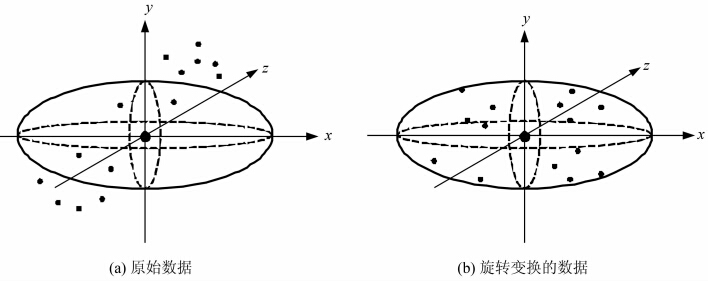 |
| 图 1 三维椭球体搜索区域Fig. 1 Searching Region of 3-Dimensional Ellipsoid |
设三维空间中采样点集S= {( x i,fi),i = 1,2,3,…,n},其中,x i = [xi yi zi]为三维坐标向量,fi为采样点的属性值,记X={ x 1,x 2,… ,x n},f = {f1,f2,…,fn},为X均值。坐标旋转步骤如下。
1) 三维空间数据协方差矩阵为:
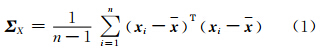
2) 对矩阵ΣX进行特征值分解:
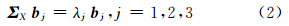
求解三个正交的特征向量,其中 λ1 ≥ λ2 ≥ λ3 ,令R=[b1 b2 b3]。
3) 将原始数据旋转变换:

空间变异函数用来表征同一时刻点不同空间点的空间变异结构[3]。通过空间变异函数计算获取的变程具有一定的地学意义,当两点间的距离(插值点与采样点之间的距离)大于变程时,认为两点之间不存在空间相关性[4]。在计算变异函数时,精确到具体方向上的数据点对较少,通过设置一定的角度容差和距离容差,获得足够的数据点对计算实验变异函数值。具体步骤如下。
1) 点对预处理。计算所有点对{(xi,xj),i ≠ j}的距离dij、变异函数值γ(dij)、点对中的最大距离dmax,剔除大于0.5dmax的点对。
2) 点对分类。设置每个轴向的角度容差为45°,比较数据点对[(xi,yi,zi),(xj,yj,zj)]的分量在所对应轴x、y、z的投影距离,记:xpd =|xi-xj|,ypd = |yi -yj|,zpd = |zi-zj|,求取三个分量中的投影距离最大值max{xpd,ypd,zpd}。将数据点对归为最大值所对应的轴,对所有数据点对进行操作,数据点对将分为三个集合且分别对应不同的三个轴。
3) 点对分组。如果集合中点对较少时,不需要分组;点对较多时,则进行分组。设分组数为n,求得分组距离容差值lagsize = 0.5dmax/ n,进行分组计算m= dij/lagsize 为第m组,对步骤2中三个集合进行相同的操作。
4) 实验变异函数的拟合。本文选取球状模型,使用RANSAC算法[5]进行球状模型的拟合,对步骤3中每个集合的分组平均值进行拟合,得到三个方向的变程分别对应于椭球体的三个轴长。
1.3 局部RBF插值方法本文采用局部RBF插值方法,即根据每个采样点的邻近范围构建节点RBF,在插值时仅需利用待插值点邻近范围内的各节点RBF的值进行加权线性组合[6]。每个节点RBF表达式为:
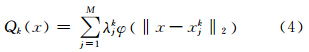
式中,φ ‖x -x kj‖2 为径向基函数;x为三维空间插值点;x kj为参考点;‖x-xkj‖2为任意插值点到参考点的欧氏距离;λkj为插值矩阵系数,其值由插值条件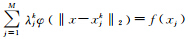 确定,其中M表示构建节点RBF的参考点个数。如图 2所示插值过程中邻近点的搜索范围,如果是各向同性的,则参考点搜索范围选择球体搜索方式,如图 2(a)所示,Rk为球体的半径,它是根据地统计中变异函数计算得到的没有顾及方向的变程;如果是各向异性的,则参考点搜索范围选择椭球体搜索方式。
确定,其中M表示构建节点RBF的参考点个数。如图 2所示插值过程中邻近点的搜索范围,如果是各向同性的,则参考点搜索范围选择球体搜索方式,如图 2(a)所示,Rk为球体的半径,它是根据地统计中变异函数计算得到的没有顾及方向的变程;如果是各向异性的,则参考点搜索范围选择椭球体搜索方式。
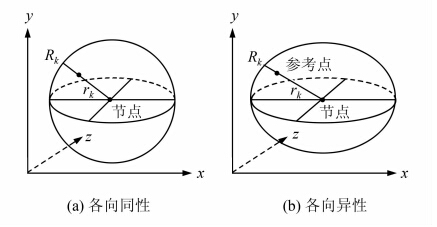 |
| 图 2 邻近范围的确定Fig. 2 Determination of Neighboring Region |
为顾及地理空间数据的各向异性,本文采用图 2(b)的搜索策略,根据§1.2节计算各轴变程设置椭球体轴长。本文选用正定的逆Multi-Quadric径向基函数保证插值矩阵的非奇异性:
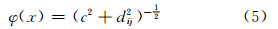
形态参数c的取值影响插值精度[7]。为了使RBF插值误差最小,采用变程范围内插值点与参考点的平均距离dn 的0.5倍作为RBF的c值[8]。对每个采样点构建节点 RBF后,计算插值点的属性值,只需将插值点搜索范围内的节点函数值进行加权组合计算,插值模型为:
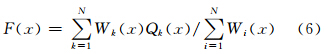
式中,
 其中,rk=√ x-xk2+ y-yk 2+ z-zk2表示已知参考点到待插值点(椭球体中心)的距离;Rk表示待插值点到椭球体的距离。
其中,rk=√ x-xk2+ y-yk 2+ z-zk2表示已知参考点到待插值点(椭球体中心)的距离;Rk表示待插值点到椭球体的距离。
令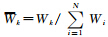 ,文献[9]证明了Wk插值权函数满足以下3个性质:
,文献[9]证明了Wk插值权函数满足以下3个性质:
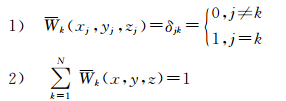


根据权函数的以上性质,可得到:
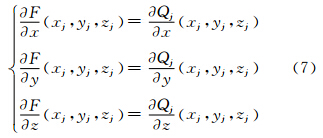
式(7)中插值函数F在节点处与节点函数的导数相同,保持了节点 RBF的局部形态特征,具有保形性。
2 实验验证
采用局部RBF插值逼近全局插值的策略进行实验,具体流程图如图 3所示。
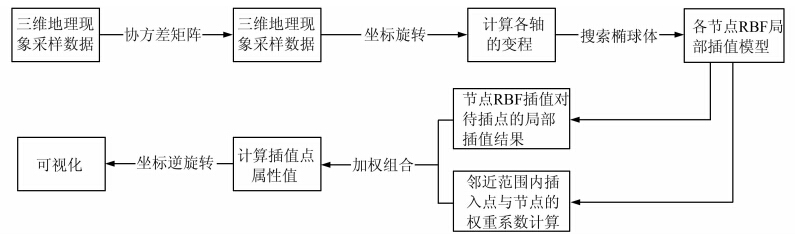 |
| 图 3 局部RBF插值流程图Fig. 3 Flow Chart of Local RBF Interpolation |
实验数据为悬沙浓度模型模拟计算的太湖某时刻三维悬沙浓度,研究区域如图 4(a)所示,数据在三维空间中呈现离散分布(见图 4(b)),共计367个三维采样点,x坐标的极差(全距)为59 312.25 m,y坐标的极差为60 336 m,z坐标的极差为2.172 1 m(z的极差很小,因为太湖区域的平均水深为1.94 m),数据在水平方向与垂直方向尺度相差较大,属性值范围为 [0.036 8,0.811 4]。在Matlab R2010b平台上,根据§1.1对数据进行坐标变换(见图 4(c)),采用§1.2节探索空间异向性方法计算出沿x、y、z三个轴向的变程值分别为2.2×104 m、1.6×104 m、0.45 m。最后分别对局部RBF(LRBF)[10]、三维普通克里金(OK)[11]、异向性OK(AOK)[12]、本文方法进行插值计算。
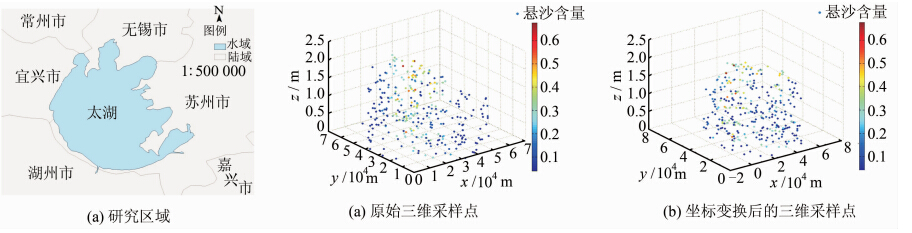 |
| 图 4 采样数据的空间分布Fig. 4 Spatial Distribution of the Sampling Data |
交叉验证法是每次假设一个采样点为未知,将余下的采样点通过某种插值方法进行估算,计算估算值与真实值的误差,对每个采样点进行相同的假设和插值估算。本文采用交叉验证方法评估插值精度,首先依次假定每个采样点的悬沙浓度属性值为未知,将余下的采样点作为已知点,使用上述的4种插值方法分别估算属性值,然后计算实际采样点的观测值与估算值的误差。对误差结果以最大误差(εmin)、最小误差(εmax)、平均误差(εme)、均方根误差(εrmse)进行评估,插值精度如表 1所示。
| 插值方法 | εmin | εmax | εme | εrmse |
| LRBF | -0.116 3 | 0.369 2 | -0.003 7 | 0.060 7 |
| OK | -0.077 1 | 0.166 2 | 0.004 3 | 0.069 2 |
| AOK | -0.051 2 | 0.236 1 | 0.002 1 | 0.038 7 |
| 本文方法 | -0.060 3 | 0.130 6 | 0.001 8 | 0.037 5 |
局部RBF插值的εmin、εmax、εme、εrmse都大于本文方法,原因是边界处搜索到的点很少或不均匀,没有顾及空间数据结构的异向性。与局部RBF插值精度类似,OK插值的4种误差都不及本文插值方法。异向性OK方法中,εmin优于本文插值方法,εmax、εme、εrmse没有本文方法精度高。两种方法的插值精度非常接近,但是本文插值方法仍优于异向性OK插值方法,主要原因是异向性OK方法需要对各个方向进行套合,而三维变异函数的套合过程非常复杂,目前仍没有一个完善的解决方法[13],在顾及空间结构的异向性情况下,本文的方法不需要套合,还具有求解矩阵方便的优点,可作为一种异向性空间插值方法。
将悬沙含量值作为属性值显示,首先求得原始采样点数据集的最小外包矩形盒,分别在x、y、z方向上进行等间距40×40×40的格网剖分,把剖分后的格网点作为插值点进行估算。由于数据垂直方向与水平方向的尺度相差很大,需要将坐标数据和属性数据进行归一化处理,以便于三维截面图显示,如图 5所示,归一化后的坐标(x,y,z)和悬沙含量值用颜色表示,红色代表属性值大,蓝色代表属性值小。图 5(d)具有更加精细的特征,原因在于本文的方法首先对已知点构建节点RBF,选取合适的权函数使得线性组合节点RBF的插值函数F不仅在节点处满足插值函数定义,且根据式(7),F的导数等于节点函数的导数,具有良好的节点保形性。
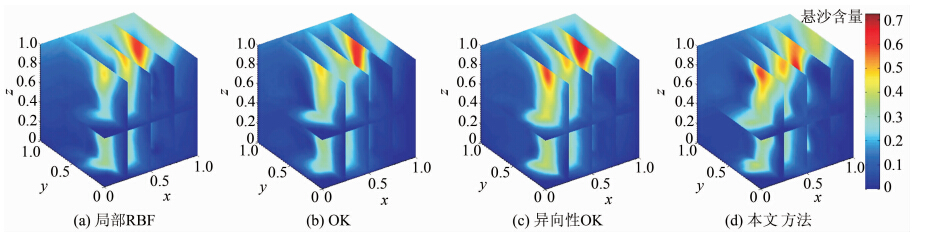 |
| 图 5 4种插值结果Fig. 5 Four Interpolation Results |
本文结合地统计中的变异函数构建了节点RBF函数,对待插值点估算采用局部线性加权组合,插值参考点的选取更加合理而且顾及了空间的各向异性,局部RBF插值保留了节点函数的局部形态特征,具有保形性。本文方法是基于RBF的,而RBF是只与径向距离有关的函数,因此,本文方法不受维度的限制,可以扩展到更高维度的插值。
| [1] | Yokota R, Barba L A, Knepley M G. PetRBF: A Parallel O(N) Algorithm for Radial Basis Function Interpolation with Gaussians[J]. Computer Methods in Applied Mechanics and Engineering, 2010, 199(25-28): 1 793-1 804 |
| [2] | Casciola G, Lazzaro D, Montefusco L B, et al. Fast Surface Reconstruction and Hole Filling Using Positive Definite Radial Basis Function[J]. Numerical Algorithms, 2005, 39(1-3): 289-305 |
| [3] | Xu Aiping, Sheng Wenshun, Shu Hong. Spatiotemporal Interpolation and Cross Validation Based on Product-Sum Model[J]. Geomatics and Information Science of Wuhan University, 2012, 37(7):766-769(徐爱萍, 圣文顺, 舒红. 时空积和模型的数据插值与交叉验证[J]. 武汉大学学报·信息科学版, 2012,37(7):766-769) |
| [4] | Chen Chuanfa, Cai Qianguang. High Speed DEM Construction Based on Local Least Squares Collocation[J]. Geomatics and Information Science of Wuhan University, 2013, 38(1):86-89(陈传法, 蔡乾广. DEM快速构建的最小二乘配置法[J]. 武汉大学学报·信息科学版, 2013, 38(1):86-89) |
| [5] | Fischler M A, Bolles R C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the Associaion for Computing Machinery, 1981, 24(6): 381-395 |
| [6] | Lazzaro D, Montefusco L B. Radial Basis Functions for the Multivariate Interpolation of Large Scattered Data Sets[J]. Journal of Computational and Applied Mathematics, 2002, 140(1/2): 521-536 |
| [7] | Zhang Jinming, You Xiong, Wan Gang. Effects of Interpolation Parameters in Multi-log Radial Basis Function on DEM Accuracy[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5):608-612(张锦明,游雄,万刚. 径向基函数算法中插值参数对DEM精度的影响[J]. 武汉大学学报·信息科学版, 2013, 38(5): 608-612) |
| [8] | Lin G F, Chen L H. A Spatial Interpolation Method Based on Radial Basis Function Networks Incorporating a Semivariogram Model[J]. Journal of Hydrology, 2004, 288(3/4): 288-298 |
| [9] | Franke R, Nielson G. Smooth Interpolation of Large Sets of Scattered Data[J]. International Journal for Numerical Methods in Engineering, 1980, 15(11): 1 691-1 704 |
| [10] | Shu C, Ding H, Yeo K S. Local Radial Basis Function-based Differential Quadrature Method and its Application to Solve Two-Dimensional Incompressible Navier-Stokes Equations[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(7/8): 941-954 |
| [11] | Bargaoui Z K, Chebbi A. Comparison of Two Kriging Interpolation Methods Applied to Spatiotemporal Rainfall[J]. Journal of Hydrology, 2009, 365(1/2): 56-73 |
| [12] | Merwade V M, Maidment D R, Goff J A. Anisotropic Considerations While Interpolating River Channel Bathymetry[J]. Journal of Hydrology, 266, 331(3): 731-741 |
| [13] | Yao Lingqing, Pan Mao, Cheng Qiuming, et al. Nested Overlap of Variograms in 3D Kriging[J]. Earth Science-Journal of China University of Geosciences, 2009, 34(2): 194-198(姚凌青, 潘懋, 成秋明, 等. 三维Kriging方法中的变异函数套合[J]. 地球科学-中国地质大学学报, 2009, 34(2): 194-198) |
 2015, Vol. 40
2015, Vol. 40



