文章信息
- 刘光明, 孟祥伟
- LIU Guangming, MENG Xiangwei
- 一种新的SAR图像局部统计活动轮廓模型及算法
- A Novel SAR Image Locally Statistical Active Contour Model and Algorithm
- 武汉大学学报·信息科学版, 2015, 40(5): 628-631
- Geomatics and Information Science of Wuhan University, 2015, 40(5): 628-631
- http://dx.doi.org/10.13203/j.whugis20130445
-
文章历史
- 收稿日期:2013-08-29
2. 91640部队, 广东 湛江, 524064
2. Unit 91640, Zhanjiang 524064, China
在SAR图像相干斑发育完全的情况下,多视SAR图像噪声一般可以认为是均值为1、方差为1/L的Gamma噪声(L是等效视数)。文献[1]基于最大后验正则化方法提出了一个针对乘积性噪声的AA(Aubert-Aujol)去噪模型[1]。本文基于AA去噪模型提出了一个新的局部统计活动轮廓模型,然后通过凸松弛技术将提出的分割模型转换成全局优化模型,再在凸优化模型中加入一个迫近算子项,通过简单的数学推导即可得到一个广义的ROF模型[2]。这样,一个具有乘性噪声图像的分割问题就转化为一个加性噪声图像的去噪问题。对于ROF模型的去噪问题,可采用文献[3, 4]提出的快速去噪算法。本文提出的算法不涉及差分或微分方程,只需要简单的差分运算,因此提高了数值运算速度。
1 新的局部统计活动轮廓模型
假设图像域Ω⊂R2是开且有界的,且 f:Ω→R是一个被乘性噪声n所污染的待分割多视SAR强度图像,可表示为f = u · n ,其中,u是真实图像。
AA模型的能量泛函可表示为[1]:
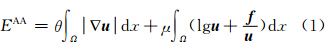
式(1)等号右边的第一项是总变分项,第二项是数据保真项,其中,μ>0和θ>0是调节参数。
为了对强度非均匀的SAR图像进行分割处理,本文提出了一个SAR图像两区域局部统计活动轮廓模型。模型的能量泛函由长度项(即边缘平滑项)和区域数据项两部分组成。先由AA模型的数据保真项得到分段常值数据项,即假定真实图像 u是分段常值的,当x∈Ω1时,u=C1;当x∈Ω2时,u=C2,然后再与高斯核函数相乘得到两区域分割数据项。本文定义局部统计活动轮廓模型(locally statistical active contour model,LACM)为:
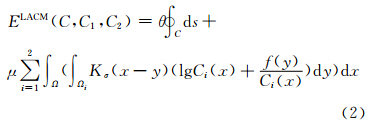
其中,Kσ(x-y)是标准差为σ的高斯核函数,高斯核函数及其定位特性在本文模型中起着重要作用。当|x-y| >3σ时,Kσ(x-y)→0,因此图像强度只有位于邻域{y: |x-y|<3σ}时,才在模型的能量泛函中起支配作用。
接着引入一个Lipschitz连续函数 φ:Ω→R(称为水平集函数),使得:
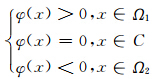
其中,{Ω1,Ω2}是图像域Ω的一个分割;C是闭合轮廓曲线(零水平集函数)。再引入Heaviside函数: 从而真实图像 u 的水平集可以表示为:
从而真实图像 u 的水平集可以表示为:
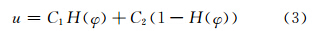
LACM模型的水平集表示为:

式(4)等号右边第一项为长度项,第二、三项是局部能量拟合数据项,第四项是惩罚函数项[5];M1=H(φ),M2=1-H(φ)。实际应用中,Heaviside函数H(φ)采用它的一个平滑近似函数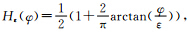 ,其中ε是一个较小的正数。
,其中ε是一个较小的正数。
对式(4)中的三个变量利用变分法进行交替优化可得:
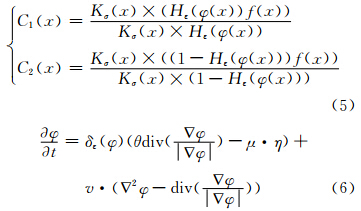
其中,

在偏微分方程(6)的数值实现中,一般采用差分近似。由于在式(4)中加入了惩罚函数项,因此式(6)的差分数值实现中,对于空间偏导数可以使用简单的中心差分近似,而时间偏导数使用前向差分实现。综上所述,基于水平集方法的LACM模型的“局部特性”使得其对水平集初始轮廓较敏感,容易陷入局部极小值。由于能量泛函ELACM (φ,C1,C2)是非凸的,ELACM(φ,C1,C2) 的全局最优解是一个困难的问题。为了克服上述问题,下文进一步对基于水平集方法的LACM模型进行凸优化处理,提出一个全局凸分割算法。此算法不但能够高效地分割具有乘性Gamma噪声的SAR图像得到一个全局最优解,而且对初始轮廓不敏感。
2 LACM模型的全局快速求解 2.1 LACM模型对应的全局优化模型首先令式(6)的θ=1且去掉最后一项,由于δε φ ≥0,式(6)可表示为式(7)(不影响水平集演化的方向并且两式具有相同的平稳解):

式(7)表示的梯度下降流水平集演化方程对应的能量泛函为:
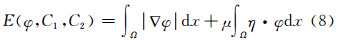
由于能量泛函E(φ,C1,C2)关于φ的均匀度为1,式(7)表示的演化方程不存在平稳解。为解决此问题,需要对φ进行凸松弛处理,即把φ限制在一个有限区间内(0≤φ≤1)。通过求解式(9)可得到能量泛函E(φ,C1,C2)唯一的全局最优解:
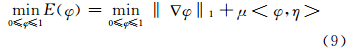
其中,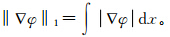
式(9)即 为LACM模型对应的全局优化模型。一旦求得全局最优解 φ(x),分割的两区域可通过阈值化水平集函数φ(x)来实现,即选取合适的γ∈(0,1),Ω1={x:φ(x)>γ},Ω2={x:φ(x)<γ}。
2.2 全局优化模型的快速求解由于式(9)中含有总变分项,其在零点处不可微,使用最陡下降法求解时一般通过添加一较小的正数来解决不可微的问题,这会导致计算效率下降。本文在式(9)中加入一个迫近算子项,通过简单的数学推导,可得到一个广义的ROF模型[2]。这样,图像分割问题就转化为一个加性噪声图像的去噪问题,而对于ROF模型的去噪问题,可采用文献[3, 4]提出的快速去噪算法实现。
1) “图像分割模型”转化为“图像去噪模型”。 本文假设式(9)中的总变分项是各向异性的,在式(9)中加入一个迫近算子项可得到:

可以看出,通过上面的简单数学转换,式(9)表示的“图像分割模型”可转换为“图像去噪模型”(式(10))。
对于式(10)采用快速去噪算法[3, 4],可得到如下快速迭代算法:
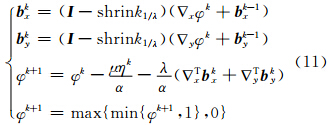
其中,shrink1/λ(x)=sgn(x)max{ x -1/λ,0}。
可以看出,迭代算法式(11)不涉及差分或微分方程,只需要简单的差分运算,因此提高了数值运算速度。
2) 利用松弛技术加快算法收敛。 为了进一步加快式(11)的收敛,本文提出松弛迭代方案:

其中,加权因子t>0为松弛参数。松弛方法通常会加快 Jacobi和Gauss-Seidel迭代算法的收敛速度。由不动点定理(fixed point theory,FPT)可得到如下结论:当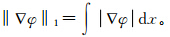 时,bxk和byk收敛,从而保证了φ(x)取得全局最优解。
时,bxk和byk收敛,从而保证了φ(x)取得全局最优解。
上述算法可用流程图表示为图 1。本文中,全局优化模型的快速算法记作FP_LACM模型。
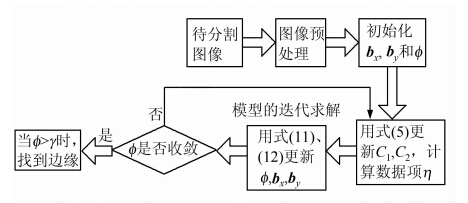 |
| 图 1 全局优化模型的算法流程Fig. 1 Diagram for the Globally Optimization Model |
采用实测SAR图像来验证和分析本文提出模型的性能。实验是在CPU为AMD 1.8 GHZ,内存为1 GB的硬件环境以及Windows XP SP2的软件环境下,采用Matlab 编程实现。将本文提出的LACM模型、FP_LACM模型与RSF模型[5]、SB_RSF模型[6]进行比较,验证本文提出模型的有效性。 SB_RSF模型和FP_LACM模型采用相同的分割阈值 γ=0.5,用来得到分割区域,即Ω1={x:φ(x)>γ}和Ω2={x:φ(x)<γ}。
 |
| 图 2 两幅SAR图像Fig. 2 Two SAR Images |
采用一幅实测Envisat SAR图像和一幅MSTAR数据库的Ku波段SAR图像,其尺寸分别为179 像素×205像素和650像素×277像素,灰度范围为0~255(见图 2)。由于RSF模型和SB_RSF模型的数据项本质上都是基于高斯分布的,从图 3、4中可以看出,RSF模型和SB_RSF模型受图像噪声影响较大,不能有效地分割非均匀SAR图像,而LACM模型和FP_LACM模型都能分割出图像边缘轮廓。表 1给出了SAR图像采用上述4种模型迭代次数和运行时间的比较。从表 1中可以看出,FP_LACM模型运行时间大约是RSF和LACM所需时间的1/33~1/23,大约是SB_RSF模型所需时间的1/3。这是因为采用了凸优化和松弛技术,使得FP_LACM模型不涉及差分或微分方程,只需要简单的差分运算,算法收敛较快,因此,FP_LACM模型比其他三种模型需要的时间大大减少。
 |
| 图 3 Envisat图像的分割结果Fig. 3 Segmentation Results of Envisat Image |
| 图像模型 | Envisat图像/ MSTAR图像 | |||
| RSF | SB_RSF | LACM | FP_LACM | |
| 次数 | 150/550 | 15/80 | 150/620 | 30/120 |
| 时间 | 253.14 s/3 442 s | 25.797 s/485.516 s | 251.719 s/3 827.8 s | 7.5 s/148.672 s |
 |
| 图 4 MSTAR图像的分割结果Fig. 4 Segmentation Results of MSTAR Image |
本文基于变分水平集方法和AA去噪模型提出一个SAR图像局部统计活动轮廓模型;然后在该模型基础上加入迫近算子项,通过简单的数学转换,提出的模型转化为广义的ROF模型;最后采用快速去噪算法,得到一个求解全局最优解的快速分割算法,算法不涉及差分或微分方程,只需要简单的差分运算;不但提高了数值运算速度,而且能较准确地检测图像的边缘。
| [1] | Aubert G, Aujol J F. A Variational Approach to Removing Multiplicative Noise[J]. SIAM Journal on Applied Mathematics, 2008, 68(4): 925-946 |
| [2] | Rudin L, Osher S, Fatemi E. Nonlinear Total Variation Based Noise Removal Algorithms[J]. Physica D, 1992, 60: 259-268 |
| [3] | Jia R Q, Zhao H. A Fast Algorithm for the Total Variation Model of Image Denoising[J]. Advances in Computational Mathematics, 2010, 33(2):231-241 |
| [4] | Jia R Q, Zhao H, Zhao W. Relaxation Methods for Image Denoising Based on Difference Schemes[J]. SIAM Journal on Applied Mathematics, 2011, 9(1): 355-372 |
| [5] | Li C, Kao C, Gore J, et al. Minimization of Region-Scalable Fitting Energy for Image Segmentation[J]. IEEE Transaction on Image Processing, 2008, 17(10): 1 940-1 949 |
| [6] | Yang Y, Li C, Kao C, et al. Split Bregman Method for Minimization of Region-Scalable Fitting Energy for Image Segmentation[C]. The International Symposium on Visual Computing, New York,2010 |
 2015, Vol. 40
2015, Vol. 40


