文章信息
- 陆苗, 梅洋, 赵勇, 冷亮
- LU Miao, MEI Yang, ZHAO Yong, LENG Liang
- 利用多尺度几何特征向量的变化检测方法
- Change Detection Based on Multi-scale Geometric Feature Vector
- 武汉大学学报·信息科学版, 2015, 40(5): 623-627
- Geomatics and Information Science of Wuhan University, 2015, 40(5): 623-627
- http://dx.doi.org/10.13203/j.whugis20130382
-
文章历史
- 收稿日期:2013-04-07
2. 农业部农业信息技术重点实验室, 北京, 100081;
3. 武汉大学遥感信息工程学院, 湖北 武汉, 430079;
4. 国家基础地理信息中心, 北京, 100830;
5. 吉林大学应用技术学院, 吉林 长春, 130022
2. Key Laboratory of Agri-informatics, Ministry of Agriculture, Beijing 100081, China;
3. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China;
4. National Geomatics Center of China, Beijing 100830, China;
5. Applied Technical College, Jilin University, Changchun 130022, China
变化检测是指在不同时期观测某一实体或现象,以此判断其状态变化的过程[1]。准确高效的变化检测信息对于研究全球变化、空间数据库更新、应急测绘保障等具有重要意义[2]。与传统像素级变化检测算法[3, 4, 5]相比,基于对象的影像分析(object-based image analysis,OBIA)[6]能综合利用影像的光谱、纹理、几何等信息,已成为近年来变化检测研究的趋势[7],而利用分割对象的几何特征则是基于对象分析的重要内容之一[8]。但是,现有方法主要采用单一尺度来进行影像分割,对多个尺度分割的规律及应用研究较少。本文提出了基于多尺度几何特征向量(multi-scale geometric feature vector,MSGFV)的变化检测方法,并以陕西省渭南市为例对该方法进行了验证分析。
1 研究区域本文选取陕西省渭南市的局部范围为研究区域,覆盖该区域的Landsat影像轨道号为P127R036。本文获取了2002-03-31的ETM+影像和2009-06-29的TM影像,如图 1所示。该区域地表覆盖类型多样,2002~2009年城市建成区面积增大,河流明显改道,具有典型的变化特征。针对原始影像,本文预处理工作包括几何纠正、大气纠正、地形纠正等。首先对两期影像进行了几何纠正,精度达到半个像素以内;然后利用ACTOR 2进行耦合大气和地形的纠正,经过大气纠正将影像的DN值转化为地表反射率,以消除大气状况不同对变化检测的影响,地形纠正则降低了地形背光和阴影对检测的影响。
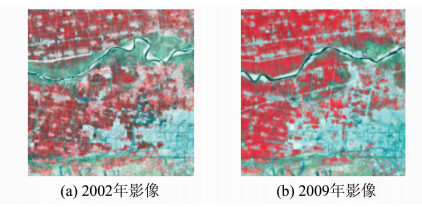 |
| 图 1 研究区域的原始影像Fig. 1 Original Imageries of Study Area |
基于MSGFV的变化检测算法基本原理是将变化检测由像素光谱空间转换到对象尺度空间,利用多尺度影像分割形成的几何特征向量来进行变化分析(见图 2)。首先,确定多尺度的数量与数值并进行多尺度影像分割;然后,以基本单元为检索条件在各个尺度分割结果中搜索尺度关联对象,计算其几何特征,并由此构建描述该检测单元的多尺度几何特征向量;最后,通过测定不同时相几何特征向量的变化强度来判断该单元的变化情况。本文将主要介绍该方法中的三个关键步骤:序列多尺度生成,多尺度几何特征向量构建,基于多尺度几何特征向量的变化强度计算。
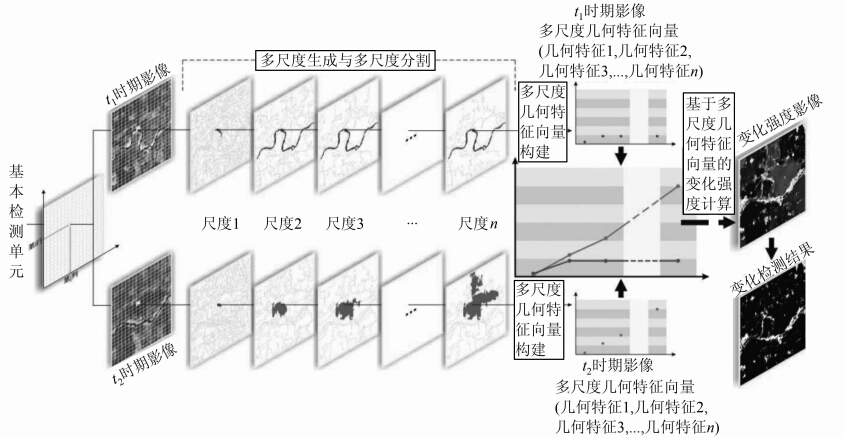 |
| 图 2 基于多尺度几何特征向量的变化检测原理Fig. 2 Methodology of Change Detection Based on Multi-scale Geometric Feature Vector |
文献[9]提出使用大、中、小三种尺度相结合的方法来研究林地要素的分类及变化分析[9]。但是,该文献中的多尺度生成与其目标对象密切相关,主要依靠经验来进行设置,难以适用于地表覆盖的变化分析。本文提出了序列多尺度的概念,它是按照一定数学规则生成的特定多尺度集合。构建序列多尺度可以使用多种数学规则,如等差序列、等比序列等。为了均匀反映影像分割对象在尺度空间中的演变规律,本文将等差数列作为序列多尺度构建的数学基础,如式(1)所示。 其中,S表示等差序列多尺度集合;a0表示序列初始值;i是从0到n的整数集合;Δ代表序列公差。尺度范围和序列公差是生成等差序列多尺度的两个主要因素。尺度范围是指等差序列多尺度集合最小值和最大值之间的范围。确定了尺度范围之后,序列公差就决定着多尺度几何特征向量刻画尺度空间的细节程度。因此,需要根据实验区及分割软件的特点来合理设置范围及公差。
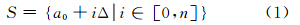
在确定了等差序列多尺度之后,需要构建多尺度几何特征向量。矢量分割对象在几何维度上属于二维面状要素,通常使用面积和周长来描述面状要素的几何特征。此外,本文还引入了景观生态学中的形状指数来描述分割对象的几何特征[8]:
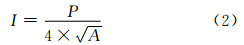
式中,I表示形状指数;A表示面积;P表示周长。本文检测方法分别使用这三种几何特征来构建多尺度几何特征向量,并以检测精度最高的结果作为最终检测结果。
多尺度几何特征向量的生成需要以基本检测单元为目标。如果将某一时相的影像分割对象作为检测单元,就要考虑影像分割的尺度以及时相选择等问题。检测对象的分割尺度可以使用序列等差多尺度中的最小值,然而使用任何一个时相的分割对象作为检测单元必然导致检测结果相对于该时相的有偏性。因此,本文选择将像素作为检测单元来构建与之对应的多尺度几何特征向量。首先,使用等差序列多尺度中的每个尺度对影像进行分割;然后,从每一尺度分割对象中搜索包含当前像素位置的尺度关联对象;最后计算所有尺度关联对象的几何特征,并组合成多尺度几何特征向量。式(3)显示了由三种几何特征形成的多尺度几何特征向量。其中,M 表示多尺度几何特征向量,A表示面积,P表示周长,I表示形状指数,g表示分割对象,n表示分割尺度。
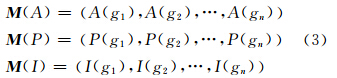
本文从多尺度几何特征向量的形状差异出发,使用相关系数来计算不同时相多尺度几何特征向量的变化强度。计算方法如式(4)所示,其中,C表示变化强度,M 表示多尺度几何特征向量,R表示相关系数,t1表示第1个时相,t2表示第2个时相,n表示多尺度的个数。由该式(4)可知,当两期多尺度几何特征向量的形状曲线相近时,其相关系数值较大,而变化强度值则较小;反之,如果形状差异大,则相关系数值较小,变化强度值则较大。
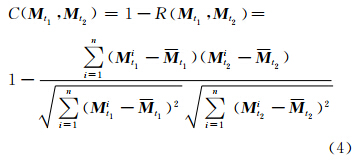
3 实验与分析 3.1 实验结果与精度评价
本文使用ENVI EX 4.7来实现遥感影像的多尺度分割,对研究区域的分割尺度范围是0~100。为了细致描述尺度空间,本文选择数值较小的5作为等差序列多尺度的公差。因此,等差序列多尺度的计算方法由式(1)转化为式(5)。图 3显示了ENVI EX 4.7对实验区2002年ETM+影像进行5、50、100尺度分割的结果。
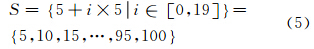
 |
| 图 3 2002年ETM+影像的分割结果Fig. 3 Segmentation Results of ETM+ Imagery in 2002 |
利用本文提出的MSGFV变化检测方法计算研究区域的变化强度,如图 4所示,包含面积、周长、形状指数三种几何特征计算的变化强度影像,图中越亮的区域表示变化的可能性越大,反之则越小。使用统计方法来设定变化阈值,该阈值由变化强度影像的平均值加上1.5倍标准差得到,变化强度大于该阈值的是变化区域,小于该阈值的是不变区域,三种变化检测的结果如图 5所示。变化区域主要集中分布在渭河沿线及城区扩张的部分,与影像目视判读的结果接近借助高分辨率影像和其他辅助资料,该实验采用分层随机抽样方法在实验区选取了不变样本35个多边形(238个像素)和变化样本16个多边形(128个像素),然后使用混淆矩阵计算了三种变化检测结果的总体精度和Kappa系数(见表 1)。基于形状指数的多尺度几何特征向量计算的变化检测结果明显优于其他两种几何特征的结果,因此,将形状指数结果作为本文在该实验区的最终结果。
 |
| 图 4 三种几何特征的变化强度结果Fig. 4 Three Change Intensity Results |
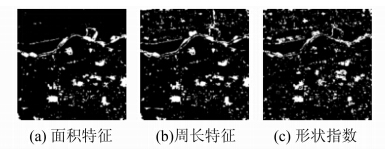 |
| 图 5 三种几何特征的变化检测结果Fig. 5 Three Change Detection Results |
| 面积特征 | 周长特征 | 形状指数 | |
| 总体精度/% | 81.15 | 83.88 | 91.26 |
| Kappa系数 | 0.542 | 0.620 | 0.807 |
利用欧氏距离、相关系数对该区域进行变化检测,并与MSGFV中的最优结果进行对比。从表 2中可看出,MSGFV形状指数方法的总体精度和Kappa系数优于其他两种方法,效果较好。
| MSGFV形状指数 | 欧氏距离 | 相关系数 | |
| 总体精度/% | 91.26 | 81.97 | 77.32 |
| Kappa系数 | 0.807 | 0.620 | 0.516 |
本文试图从影像分割的尺度空间出发,建立一种新的面向对象的变化检测分析方法。该方法将检测的依据从光谱空间转换到尺度空间,通过等差序列多尺度的生成、多尺度几何特征向量的构建、基于几何特征向量的变化强度计算等关键步骤来实现变化区域的测定。本文通过对比分析三种几何特征及传统检测方法在研究区域的检测精度,说明了本文方法在变化检测精度上的提升。本文还将针对多尺度分割对象其他特征的应用、不同影像软件的多尺度分割结果与检测精度之间的关系等问题开展后续研究,从而实现面向检测区域特点的自适应多尺度构建及变化检测。
| [1] | Singh A. Digital Change Detection Techniques Using Remotely-Sensed Data[J]. International Journal of Remote Sensing, 1989, 10(6): 989-1 003 |
| [2] | Wu C, Du B, Zhang L. Slow Feature Analysis for Change Detection in Multispectral Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, DOI:10.1109/TGRS.2013.2266673 |
| [3] | Ma Guorui, Sui Haigang, Li Pingxiang, et al. A Kernel-Based Similarity Measures for Change Detection in RS Images[J]. Geomatics and Information Science of Wuhan University, 2009, 34(1): 19-23(马国锐,眭海刚,李平湘,等. 基于核函数度量相似性的遥感影像变化检测[J]. 武汉大学学报·信息科学版, 2009, 34(1): 19-23) |
| [4] | Lu Miao, Mei Yang, Chen Lijun. Land Cover Change Detection Based on Value and Shape Optimized Combination[J]. Geomatics and Information Science of Wuhan University, 2013, 38(6): 669-673(陆苗,梅洋,陈利军. 利用光谱量值和形状优化组合的地表覆盖变化检测方法[J]. 武汉大学学报·信息科学版, 2013, 38(6): 669-673) |
| [5] | Chen J, Lu M, Chen X, et al. A Spectral Gradient Difference Based Approach For Land Cover Change Detection[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 85: 1-12 |
| [6] | Blaschke T. Object Based Image Analysis for Remote Sensing[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65: 2-16 |
| [7] | Hussain M, Chen D, Cheng A, et al. Change Detection from Remotely Sensed Images: From Pixel-Based to Object-Based Approaches[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 80: 91-106 |
| [8] | Jiao L, Liu Y, Li H. Characterizing Land-Use classes in Remote Sensing Imagery by Shape Metrics[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 72: 46-55 |
| [9] | Lamonaca A, Corona P, Barbati A. Exploring Forest Structural Complexity by Multi-scale Segmentation of VHR Imagery[J]. Remote Sensing of Environment, 2008, 112: 2 839-2 849 |
 2015, Vol. 40
2015, Vol. 40



