文章信息
- 付海强, 汪长城, 朱建军, 解清华, 赵蓉
- FU Haiqiang, WANG Changcheng, ZHU Jianjun, XIE Qinghua, ZHAO Rong
- Neumann分解理论在极化SAR植被分类中的应用
- A Polarimetric Classification Method Based on Neumann Decomposition
- 武汉大学学报·信息科学版, 2015, 40(5): 607-611
- Geomatics and Information Science of Wuhan University, 2015, 40(5): 607-611
- http://dx.doi.org/10.13203/j.whugis20130372
-
文章历史
- 收稿日期:2013-07-31
极化SAR具有对观测目标的形状和方向敏感的特征[1, 2]。基于模型分解的极化分类方法是众多极化分类方法中的研究热点,研究的关键在于如何准确描述植被的形态特征。本文以Neumann分解模型为基础,利用其可以表征散射粒子形状及空间分布随机程度的特性,提出了一种Wishart-Neumann极化SAR分类法。该方法以Neumann分解结果作为Wishart迭代的初值,进行分类,旨在解决传统基于模型分解的分类方法无法识别不同类型植被的问题。最后,本文通过机载L波段E-SAR数据及L、C波段SIR-C/X-SAR数据进行了实验。
1 基于Neumann分解理论的极化SAR分类方法 1.1 Neumann分解理论
目前,研究植被覆盖区域最为常用的模型为随机散射体模型(random volume over ground,RVoG),即将植被覆盖区分为植被层和地表层[3]。其中,植被层被抽象成由各向同性的散射粒子构成。利用该模型对极化雷达信号进行表达,即可反演表征植被层特征的参数,进而对植被层进行定量描述。模型与真实情况的贴合程度决定了反演参数的可靠性。2010年,Neumann提出一种新的模型来表达微波与植被覆盖区的作用过程[2]。该模型原理如下。
基于二阶统计的Pauli基矢量化后的散射矩阵可以表达成:
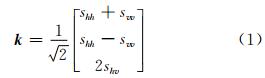
以此为基础,极化相干矩阵可以表达为:

E()表示取平均;†表示共轭转置。在Neumann理论中,假定方向角与其他描述植被形态特征的参数独立的条件下,相干矩阵的表达式为:

其中,*表示共轭;fv为散射强度归一化因子; R T(2φ)表示旋转矩阵;φ为平均方向角,Lee证明了方向角对Freeman模型分解不同散射机制散射强度的影响,并推导出其计算公式[6]; δ代表散射粒子的各向异性,为复数,描述散射粒子在极化平面内的形状,当 δ →0时,粒子为球形,δ →1时,粒子为极子,如图 1(a)所示;gc、g 取决于植被层散射粒子方向角服从的概率分布,与Freeman[4]和Yamaguchi[5]分解法假定散射粒子方向角服从均匀分布不同,Neumann假定其服从圆正态分布[2]:

|
| 图 1 各向异性及方向角随机程度示意图 Fig. 1 Schematic Representation of Anisotropy and Orientation Randomness |
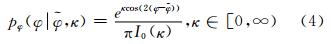
其中,κ表示集中程度;In(κ)表示n次 Bessel函数。利用Bessel函数对 gc、g进行表达,具体参见文献[2],并定义方向角随机程度τ:

τ值变化范围为0~1,值越大,表征粒子在极化平面内分布的随机程度越高,如图 1(b)所示。将g、gc表达为方向角随机程度τ的函数并利用线性方程对g、gc进行近似,得到相干矩阵:
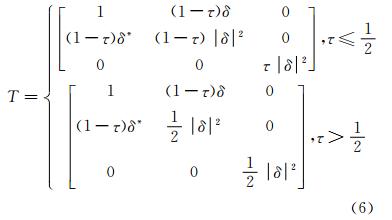
联合式(2)、(6),可以解算出各向异性δ及方向角随机程度τ,由于各向异性δ为复数,利用δ对应的模及相位进行表达:
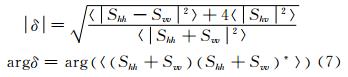
〈〉表示取均值。 Neumann证明了各向异性与Cloude分解理论中的α存在如下关系: δ =tanα。方向角随机程度的表达式为:
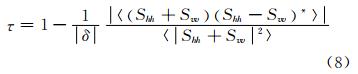
文献[2]中研究发现各向异性与植被种类存在一定关联[2],这为利用极化数据区分不同种类的植被提供了重要信息。此外,由于不同类别的植被其树叶、枝干等结构空间分布呈现显著差异,而方向角随机程度正是能对这一差异进行表达,进而方向角随机程度在各向异性的基础之上又提供了更加完备的信息对植被的形态特征进行表达。故本文以各向异性及方向角随机程度对植被的形态特征加以区分,进而达到分类的目的。 1.2 Wishart-Neumann极化SAR分类法
各向异性 δ 描述了散射粒子在极化平面内所体现的平均形状,方向角随机程度τ描述了散射粒子在极化平面内分布的随机程度。Lee提出极化SAR非监督分类方法[7],该方法的主要思想为:利用H/α分解理论,依据不同的散射机制对地物进行划分,进行初始分类;之后,根据极化相干矩阵服从Wishart分布的特点,利用Wishart距离进行迭代分类。Neumann理论中,δ 、τ与H/α 分解理论中α、entropy表征相似的物理意义。故本文借鉴该分类思想,首先利用 δ 与τ按照H/α平面划分原则对极化SAR数据进行初始分类,之后,利用Wishart进行迭代分类。Wishart距离的表达式为[7]:
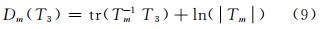
其中,
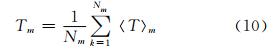
本文分类流程如图 2所示。

|
| 图 2 新方法分类法流程图 Fig. 2 Flow Chart of New Method |
为了验证本文方法的可行性,选取德国Oberpfaffenhofen地区作为实验区域进行实验。收集了该地区两种平台的全极化数据,数据的具体参数见表 1。
图 3为Pauli基彩色合成图。a、b、c、d为研究区域对应的阔叶林、机场、农田及针叶林4种典型地物,其中,b区域同时给出了E-SAR数据Pauli基彩色合成图及光学遥感影像。由A、B可以看出SIR-C/X-SAR C波段与L波段反映的地物纹理特征有明显差别,相比而言,L波段数据呈现的纹理信息更为丰富,可以清晰区分出森林覆盖区与农田覆盖区。 C为机载E-SAR L波段全极化数据,其相比SIR-C/X-SAR数据展现出良好的纹理特性。红色矩形框为分类研究区域。

|
| 图 3 实验区数据 Fig. 3 Data of Study Area |
在图 3中C图左上角,有一块较大的林地。林区以自然针叶林为主,其中混有少量面积的阔叶林及低矮植被[12]。已有研究中,均利用该数据得到了满意的结果,但是,这些研究只是将植被从其他地物中区分开来,并没有对不同种类的植被进行很好的区分[9, 10, 11]。
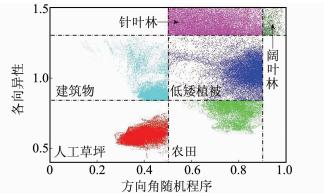
图 4为研究区域典型地物对应的各向异性/方向角随机程度二维分布平面,具体划分原则参见文献[2, 7]。由该分布图可以看出 δ /τ对不同地物具有较好的区分现象。理论上,在Born近似条件下,δ 的取值范围为0~1,对于出现大于1的原因,Neumann指出可能主要在于模型未能考虑更为复杂的散射过程或有效地将地面散射成分分离所致[2]。可以看出,建筑物与人工草坪具有相对较小的方向角随机程度;针叶林相比低矮植被、农田具有较大的 δ ;阔叶林相比针叶林具有较高的方向角随机程度。
|
| 图 4 各向异性/方向角随机程度二维平面 Fig. 4 Two Dimensional Anisotropy/Randomness Plan |
之后,利用Wishart迭代进行聚类分析得到最终分类结果。为了验证本文方法在植被覆盖区分类的优越性,本文同时给出了Wishart-Freeman[4]和Wishart-Yamaguchi[5]的分类结果,如图 5所示。根据文献[12]中实地调查资料及目视判别Google Earth不同年份的遥感影像及地面实景相片可知,研究区域主要地物类别为农田、针叶林、落叶林、低矮植被、道路、人工草坪、建筑。其中,利用冬季获取的遥感影像数据(冬季该区域阔叶林树叶脱落)及地面实景照片可以较为清晰确定阔叶林的空间分布。对于森林覆盖区,本文算法将其分为低矮植被区、针叶林区、落叶林区三类。而已有方法未能将针叶林与阔叶林加以区分(图 5中B、C、D标定区域,可以清晰看到B为针叶林,C和D为阔叶林)。

|
| 图 5 E-SAR数据分类结果 Fig. 5 Classification Results of E-SAR Data |
对于农田覆盖区(图 5中A标定区域),Whiart-Freeman与本文算法分类效果较为相近,而Wishart-Yamaguchi算法将大面积的农田覆盖区误分为人工草坪。整体上来看,本文算法可以较好地将农田区与其他地物进行区分,但是仍存在局部错分现象,如将农田误分为人工草坪(图 5椭圆标定区域),分析原因可能为该区域覆盖的农作物的形态特征与人工草坪较为相近。
对于人工构造物(建筑区及道路),本文算法在道路区域发生明显错分现象,对于建筑物的识别能力与前两种算法相当,存在明显的错分现象。原因在于Neumann分解理论主要表征植被覆盖区域的散射特性,对人工构造物辨识度较差。
总的来说,本文算法相比已有算法在林地获得了较好的分类结果;在农田地区其分类效果与Wishart-Freeman分类效果相当,优于Wishart-Yamaguchi分类效果。对于居民地,3种方法分类效果均不理想。
2.3 SIR-C/X- SAR数据实验
为了进一步验证本文算法的可行性,本文利用SIR-C/X-SAR数据进行实验,其覆盖范围包含E-SAR数据的覆盖范围。图 6为C、L波段极化数据分类结果。相比C波段极化数据,L波段数据分类结果更优,原因在于L波段相比C波段具有较强的穿透能力,回波信号中包含了更多的植被枝干信息,解算得到的 δ 、τ更能准确反映植被的形态特征,进而得到更好的分类结果。

|
| 图 6 SIR-C/X-SAR数据分类结果 Fig. 6 Classification Results of SIR-C/X-SAR Data |
由L波段的分类结果可以看出,Wishart-Neumann方法将研究区域划分为针叶林、阔叶林、低矮植被、农田、居民地、水体6种主要地物要素。图 6中同时给出标定的6个典型区域(A、B、C、D、E、F)及对应区域的遥感影像或地面实景照片,分类结果与光学影像呈现的类别较为一致,说明了本文分类算法的合理性。研究区域的阔叶林主要呈线状分布,与道路位置对应,结合多处实景照片,发现在道路两侧主要以阔叶林为主,见图 6中实景照片D所示。对于混有较多植被的居民地,本文算法将建筑区误分为低矮植被,如图 6中E对应区域。而当居民区植被较少时,居民区得到较好的识别,如图 6中F对应区域。
3 结 语
本文提出了一种基于Neumann分解理论的Wishart-Neumann分类法。该分类模型引入了各向异性及方向角随机程度来表征植被的形态特征,根据不同种类植被形态特征的差异达到分类的目的。本文方法相比传统的分解模型(Freeman分解及Yamaguchi分解),在植被覆盖区可以较好地区分植被类别,对于林业普查具有重要的研究价值及应用前景。但是,本文提出的分类方法仍存在一些不足之处有待于深入研究。比如,如何准确建立随机程度、各向异性与不同植被种类之间的关联,做到更为精细化的分类;植被覆盖区散射机制一定程度上依赖于植被密度的变化,植被密度对分类结果有何影响也有待进一步研究。
| [1] | Wang Y T,Ainsworth T L, Lee J S. Estimation of The Orientation and Shape Parameters of Canopy Scatterers from POLSAR Observations[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(3): 835-846 |
| [2] | Neumann M, Ferro-Famil L, Reigber A. Estimation of Forest Structure, Ground, and Canopy Layer Characteristics from Mutibaseline Polarimetric Interfero-metric SAR Data [J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3):1 086-1 103 |
| [3] | Trueuhaft R N, Siqueira P R. Vertical Structure of Vegetatedland Surfaces from Interferometric and Polarimetric Radar[J]. Radio Science, 2000, 35(1): 141-177 |
| [4] | Freeman A, Durden S L. A Three-component Scattering Model for Polarimetric SAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 963-973 |
| [5] | Yamaguchi Y, Moriyama T, Ishido M, et al. Four-component Scattering Model for Polarimetric SAR Image Decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(8): 1 699-1 706 |
| [6] | Lee J S, Ainsworth T L. TheEffect of Orientation Angle Compensation on Coherency Matrix and Polarimetric Target Decomposition [J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 9(1):53-64 |
| [7] | Lee J S, Grunes M R, Pottier E, et al. Unsupervised Terrain Classification Preserving Polarimetric Scattering Characteristics[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42 (4):722-731 |
| [8] | Cloude S R, Pottier E. AReview of Target Decomposition Theorems in Radar Polarimetry Data [J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(2):498-518 |
| [9] | Zhao Lingli, Yang Jie, Li Pingxiang, et al. Statistical Classification of Weak Backscattering Scatterers of PolSAR Image[J]. Journal of Remote Sensing, 2013,17(2): 306-319(赵伶俐, 杨杰, 李平湘等. 极化 SAR 影像弱散射地物统计分类[J]. 2013, 17(2): 306-319) |
| [10] | Zou Tongyuan, Yang Wen, Dai Dengxin, et al.An Unsupervised Classification Method of POLSAR Image[J]. Geomatics and Information Science of Wuhan University, 2009, 34(8): 910-913(邹同元, 杨文, 代登信,等. 一种新的极化SAR图像非监督分类算法研究[J]. 武汉大学学报·信息科学版, 2009, 34(8): 910-913) |
| [11] | Yang Jie, Zhao Lingli, Li Pingxiang, et al. Preserving Polarimetric Scattering Characteristics Classification by introducing Normalized Circular-pol Correlation coefficient[J]. Geomatics and Information Science of Wuhan University, 2012, 37(8): 911-914(杨杰,赵伶俐, 李平湘,等. 引入规范化圆极化相关系数的保持极化散射特性的分类算法. 武汉大学学报·信息科学版, 2012, 37(8): 911-914) |
| [12] | Papathanassiou K P, Cloude S R. Single-Baseline Polarimetric SAR Interferometry[J]. IEEE Transactions on Geoscienceand Remote Sensing, 2001, 39(11): 2 352-2 362 |
 2015, Vol. 40
2015, Vol. 40



